,
,
,
,
2. 北京大学 工学院, 北京 100871;
3. 华中科技大学 自动化学院, 湖北 武汉 430074
,
,
,
,
2. College of Engineering, Peking University, Beijing 100871, China;
3. School of Automation, Huazhong University of Science and Technology, Wuhan 430074, China
协同定位是多机器人导航领域的一项关键技术，也是多机器人进行其他行为的前提，它是指一群机器人在共同的环境下，通过共享环境信息，融合不同机器人的观测信息，逐步消除累计误差，实现在共同环境下确定各自机器人的位姿信息。与单个机器人定位相比，协同定位拥有更多的观测信息，故具有更好的定位精度。文献[1]运用卡尔曼滤波器(Kalman filter,KF)及粒子滤波器(particle filter)，通过增量评估机器人位姿和环境特征位置后验概率的方法使机器人在探索未知环境中，能够递增地建立地图同时对路标进行定位，但此算法复杂性高，实时性不强。 文中将无线传感器网络(wireless sensor network,WSN)应用于多机器人协同定位系统，无线传感器网络即是计算机通信和传感器多领域技术相结合的产物，也是将信息获取(传感)、信息传递与信息处理相结合的产物，它是将部署在监测区域的大量具有有限计算能力的微型传感器节点相互协作构成的一个多跳自组织网络，因其能在复杂环境下实时检测和远程监控而广泛应用于工业控制、安全监测、仓库管理和空间搜索等领域[4]。 文中应用无线传感器网络节点作为机器人定位的特定标识，利用WSN环境下粒子群优化的多机器人协同定位算法，使用带有权重的的粒子多次迭代估计出机器人运动的位置。
1 WSN环境粒子群优化协同定位算法 1.1 粒子群优化原理粒子群优化算法源自鸟群捕食行为原理，每个鸟可以看成是空间里面的一个不计体积和质量的微粒，初始化的微粒位置为待优化问题的潜在解，也就是待解决目标函数的解，粒子在空间移动时能记录个体最优值pbest和全局最优值gbest，每一次迭代后，粒子改变移动的位置和速度，从而更新全体及个体最优值，最终全体最优值为目标函数的解。文中粒子全体最优解为机器人真实位置。
此法假设搜索空间为D维，随机初始化粒子的位置及速度。设粒子群中第i个粒子的位置表示为k,第i个粒子的速度表示为 xi=[xi1 xi2 … xid]，第i个粒子的速度表示为vi=[vi1 vi2 … viD]，第i个粒子迄今为止搜索的最好位置记为pi=[pi1 pi2 … piD], 整个粒子迄今为止搜索到的最好位置记为wjki∝wjk－1ip(zjk|Xki)。评价每个粒子的适应度，将当前各粒子的位置和适应度存储在各微粒的pbest中，将所有的pbest中适应值最优个体的位置和适应值存储于gbest中，对于每一个粒子，在w1ki,w2ki,…,wnki维(1≤d≤D)空间下，速度与位置方程对粒子新的预测位置进行更新[6]。根据等式(1)进行变化：
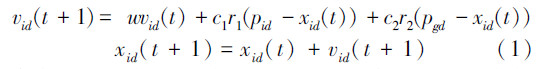
实际实验中惯性权重值大的适用于全局粒子搜索，权重值小的适用于局部搜索。
随着迭代次数的增多，粒子逐渐逼近机器人的真实位置，由于希望算法的局部搜索能力强，因此惯性权重以递减的形式设计，惯性权重的计算与多传感器信息融合相结合，借助无线传感器网络节点的观测模型来更新每个粒子的权重，实现多传感器的信息融合。假设每个机器人身上放置一个无线传感器节点，在k时刻，第i个机器人Xki(xik,yik,zik)在移动的过程中，周围有n个无线传感器节点被激活(包括周围机器人身上的节点)，只在机器人到达周围无线传感器网络感知范围时节点才被激活，如图 1所示。
图 1中虚线圆为无线通信节点的通信范围，设第i个机器人周围被激活的这n个节点的观测模型用ZK=zk1,zk2,…，zkn表示，设第j个节点对应的坐标为(XjK,YKj,ZKj)，其对应的观测模型为
 |
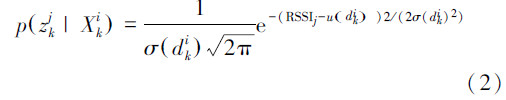
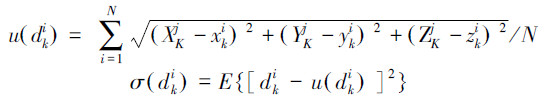
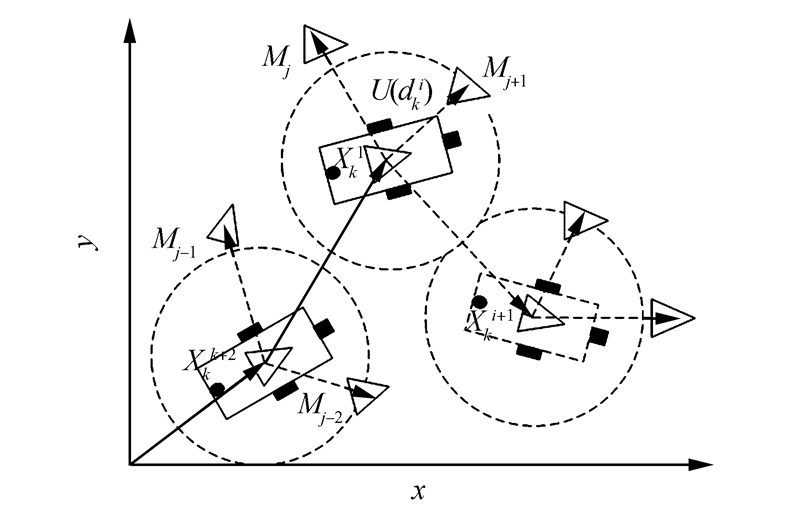| 图 1 机器人系统状态Fig. 1 The state of the robot |
由此可得这n个节点对应的似然度为
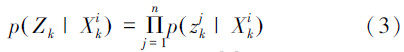
文中借鉴序贯蒙特卡洛方法[8]，利用一组带有权重的采样点来趋近状态的后验概率密度函数。粒子的权重表示为
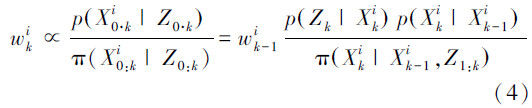
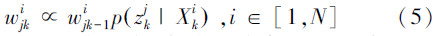
总共选取n个节点，每个节点都对粒子产生影响，那么每个粒子得到一组权重{w1ki,w2ki,…,wnki}。
1.3 重采样更新完粒子的权重后，很多粒子的权值过小，这些权值过小的粒子在计算中增加了计算时间且对结果无益，故希望通过重采样的方式将权重较大的粒子留下来，舍去权重较小的粒子，实际上重采样是为了集中粒子到高似然区域，以提高对将来状态的估计，实际应用中往往不能对后验分布p(X0:n|Z0:n)进行采样，文中使用一种简单的方法如式(6)：
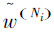为粒子权重的归一化结果,将此式与设定的阈值Neff进行比较，如果此式比阈值大则不需进行重采样，如果此式比阈值小(Neff≤N/2)，则进行重采样。 算法选定的采样函数 
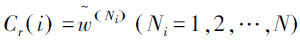用来对粒子进行重采样，i为粒子序号，重采样后粒子的权值都设定为1/N。
1.4 适应度函数
当高权重粒子在多次迭代过程中逐步趋近高似然区域的时候，需要有一个函数来判断趋近真实位置的程度，文中选用适应度函数来判断粒子群优化算法对移动机器人预测位置的优化程度[9]，适应度函数如式(7)：
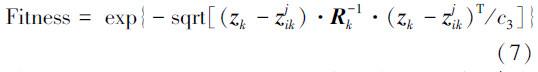
无线传感器环境下粒子群优化的多机器人协同定位算法，通过多传感器信息融合、更新粒子权重、重采样、以及自适应函数判断最终位置来实现多机器人协同定位，其算法的流程图如图 2所示。
 |
| 图 2 实验算法流程图Fig. 2 Flow chart of the algorithm |
采用MATLAB7.0对本实验进行仿真，在仿真实验中采用的观测噪声和状态噪声均为高斯噪声，噪声的通带截止频率为wp=2.5E6,3.5E6，阻带截止频率为ws=2E6,4E6,通带最大衰减1 dB和阻带最小衰减60 dB由一个巴特沃斯滤波器产生，滤波后的噪声分布及频谱图如图 3所示。
 |
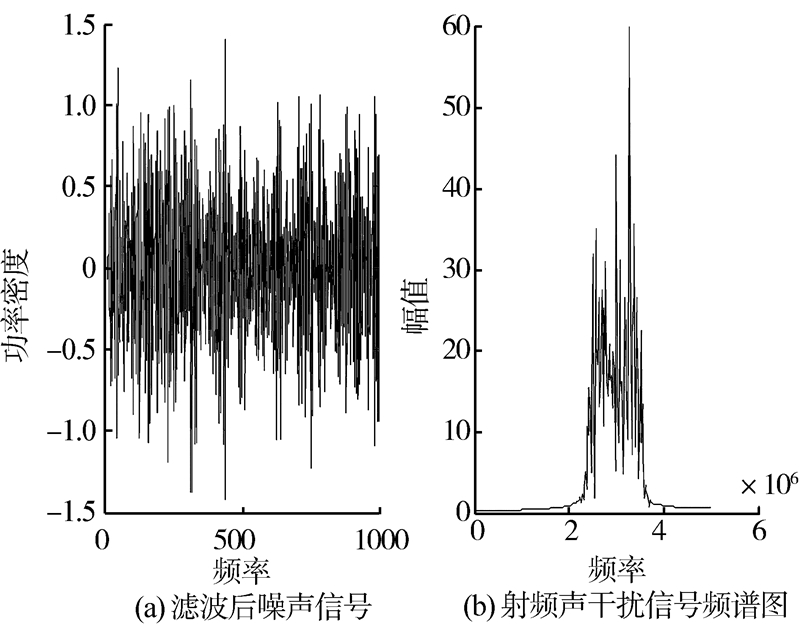| 图 3 系统产生的高斯噪声及对应的频谱图Fig. 3 Spectrum Gauss noise and the corresponding system |
三维环境的创建借鉴MATLAB7.0中改进的peaks函数，应用此函数便于仿真时在三维环境下直观地观测节点和机器人的位置。
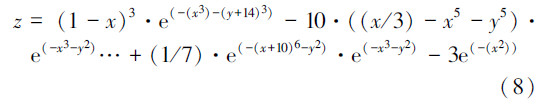
对于多机器人定位，只需得到单机器人位置，以同样的方式就能得到其他机器人的位置。假定3个机器人位置(也是节点的位置)分别为(-0.1,1.6,6.5)，(1.0,-0.1,3.0)，(0.21,0.71,0)，地图上放置6个无线传感器节点(0,0,-15)，(-3.5,6,0.5)，(-3.5,-6,0.5)，(3.5,-6,0.5) ，(3.5,6,0.5) ，(0,0,10)。其通信距离为4 m，以第一个机器人的位置为例，为了让粒子估计迅速收敛到真实的位置附近，需经多次实验验证，实验采用的重要参数为：c1=2，c2=2，种群大小 pop_size=40，最大迭代次数ma_gen=80，权系数最大值0.9,最小为0.4,如图 4所示，图 4是在迭代次数40及80次的时候粒子位姿状态，圆表示机器人，星号表示粒子，菱形表示无线传感器节点。
 |
| 图 4 迭代时的粒子分布Fig. 4 The particle distribution of iteration |
当迭代次数达到80时，粒子各自找到自己的最优位姿并且集中收敛在一个位姿附近，假定80%的粒子处于一个最小空间球中(除开边界的少数不合理的粒子)，这80%粒子的三维坐标值的均值就设定为团体最优值(即估计的机器人的位置)。经过实验仿真计算，团体最优值为gbest =(-0.008 5,1.582 3,6.479 8)，由图 5所示,使用MATLAB7.0，Figure-Tools-Date Cursor操作粗略估计机器人的位置为(-0.1,1.6,6.5)。下面介绍一个机器人在Z、X坐标不变的时候(另外2个机器人不变)，Y坐标动态发生变化的情况，实验进行了50次，如图 6所示。横坐标为运算的次数，纵坐标为Y轴方向的机器人真实位置(黑色小点表示)和估计位置(黑色星号表示)，实验中选定一个位置(24,2.021)，发现对应的预估计的位置为(24，0.627 3)，Y轴误差为1.393 7 m，其他的点可由图形上观测，可见WSN环境下移动机器人的节点定位误差在机器人移动时存在且不稳定，但相对误差较好，误差程度较平稳，系统冗余度、可靠性较好，基本上解决了粒子重采样时出现的粒子退化现象。
 |
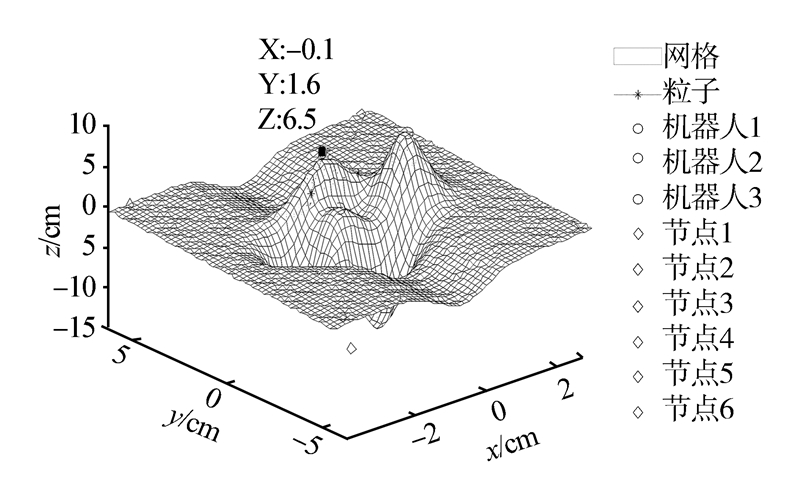| 图 5 迭代80次粒子估计的位置Fig. 5 80 iterative estimation of the particle position |
 |
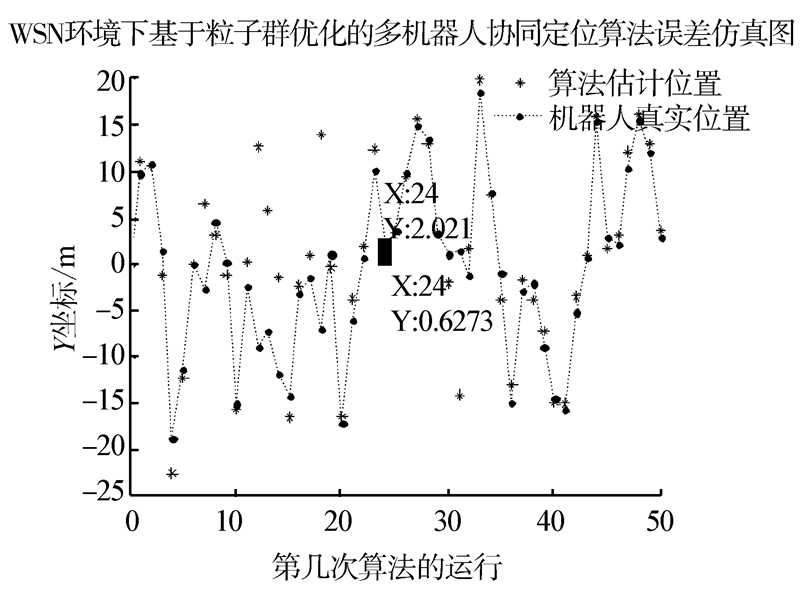| 图 6 多移动机器人协同定位误差Fig. 6 Multi-robot cooperative localization error |
多机器人协同定位算法实验误差分析如表 1。
| 粒子数 | 迭代50次 | 迭代55次 | 迭代60次 | 迭代70次 |
| 20 | 0.378m (9.34s) | 0.314m (9.45s) |
0.316m (10.34s) | 0.318m (11.32s) |
| 30 | 0.314m (10.23s) | 0.232m (11.65s) | 0.226m (12.43s) |
0.216m (13.23s) |
| 40 | 0.317 m (12.34 s) | 0.243 m (13.45 s) | 0.221 m (14.76 s) | 0.207 m (15.01 s) |
| 50 |
0.327 m (14.56 s) |
0.234 m (15.67 s) |
0.216 m (16.78 s) | 0.206 m (17.69 s) |
为进一步验证算法的实时性能以及定位精度，将此算法在机器人位置固定不变时，以不同粒子数和迭代次数进行实验，对应求出算法运行时间(s)和定位精度(m)如表 1所示。由表 1可知,迭代次数越大、粒子数越多，相应的定位精度也越准确，可是相应的时间也增大，算法的时效性不够，为满足不同的定位要求，可适当调整相应的参数以满足实验要求。
4 结 论文中将无线传感器系统与粒子群优化算法相结合以实现多机器人协同定位。无线传感器网络辅助机器人定位，实现了节点间的信息融合，在定位中引入重采样，多次迭代更新粒子状态，减少了冗余节点的影响。仿真结果表明，本方法能够有效地进行定位，满足了定位精度要求，今后将研究算法的时效性问题以满足快速定位的要求。
| [1] | SAYED H, TARIGHAT A, KHAJEHNOUR N. New work based wireless location [J]. IEEE Signal Processing Magazine, 2005, 22(4): 24-40. |
| [2] | 海丹, 李勇, 张辉,等. 无线传感器网络环境下基于粒子滤波器的移动机器人SLAM算法[J].智能系统学报, 2010, 5(5): 1673-4785.HAN Dan, LI Yong, ZHANG Hui, et al. Wireless sensor network environment of mobile robot SLAM algorithm based on particle filter[J]. Journal of Intelligent Systems, 2010, 5(5): 1673-4785. |
| [3] | 李会荣, 高岳林. 粒子群优化的速度方程改进与自适应变异策略[J]. 计算机工程与应用, 2010(13), 13: 47-50.LI Huiyong, GAO Yuelin. Particle swarm optimization improved velocity and adaptive mutation strategy[J]. Computer Engineering and Application, 2010(13): 47-50. |
| [4] | 刘利枚, 蔡自兴. 基于改进的粒子群优化的FastSLAM方法[J]. 高技术通讯, 2011, 21(4): 422-427.LIU Limei, CAI Zixin. FastSLAM method based on improved particle swarm optimization[J]. High Technology Communication, 2011, 21(4): 422-427. |
| [5] | SUN G L, CHEN J, GUO W. Signal processing techniques in network-aided position[J]. IEEE Signal Processing Magazine, 2005, 22(2): 12-23. |
| [6] | ROUMELIOTIS S, BEKEY G. Distributed multi-robot localization[J]. IEEE Transactions on Robotics and Automation, 2002, 18(5): 781-795. |
| [7] | LI Z, GHOSH B. Line segment based map building and localization using 2D laser Range finder[C]//IEEE Conference on Robotics and Automation, Karlsruhe,Germany, 2000: 2538-2543. |
| [8] | VLASSIS N, MOTOMURA Y, KROSE B. Supervised linear feature extration for mobile robot Localization[C]//IEEE Conference on Robotics and Automation. Karlsruhe,Germany, 2000: 2979-2984. |
| [9] | MOMESNO L, GASPAR J, VICTOR J. Cooperative localization by fusing vision-based bearing measurements and motion[C]//IEEE/RSJ International Conference on Intelligent Robots and Systems. Edmonton, Canada, 2005: 19-24. |
| [10] | BERTALMIO M. Filling in by joint interpolation of vector fields and grey levels[J]. IEEE Transactions on Image Processing, 2001, 10(8): 1200-1210. |
| [11] | ALAMI R, FLEURY S, HERRB M, et al. Multi-robots cooperation in the MARTHA project[J]. IEEE Robotics and Automation, 1998, 5(l): 36-47. |
| [12] | LUO R C, LI J X, CHEN C T. Indoor localization using line based map for autonomous mobile robot[C]//IEEE Workshop on Advanced Roboties and its Social im Pacts, 2008: 1-6. |
| [13] | XIA Y M, YANG Y M. A new particle fllter and its applieation in mobile robot localization[C]//International Conference on Fuzzy Systems and Knowledge Diseovery. Jinan, China, 2008: 522-525. |
| [14] | GUIVANT J, NEBOT E. Optimization of the simultaneous localization and map building algorithm for real time imPlementation[J]. IEEE Transactions on Robotics and Automation, 2001, 17(3): 242-257. |
| [15] | KIM C, SAKTHIVEL R, CHUNG W K. Unscented FastSLAM: a robust and efficient solution to the SLAM Problem[J]. IEEE Transactions on Robotics, 2008, 24(4): 808-820. |
| [16] | FOX D, KO J. Distributed multirobot exploration and mapping[J]. Proceeedings of the IEEE, 2006, 94(7): 1325-1339. |
| [17] | BARSHAN B, DURRANT W H. Inertial navigation systems for mobile robots[J]. IEEE Trans Robot Autom, 1995, 11(3): 328-42. |
| [18] | DISSANAYAKE M, NEWMAN P, CLARK S, et al. A solution to the simultaneous localization and map building (SLAM) problem[J]. IEEE Trans Robot Autom, 2001, 17(3): 22-41. |
| [19] | DURRANT W H, BAILEY T. Simultaneous localization and mapping (SLAM): part I[J]. IEEE Robot Autom Mag, 2006, 13(2): 99-110. |
| [20] | ARULAMPALAM M, MASKELL S, GORDON N, et al. A tutorial on particle filters for online nonlinear Bayesian tracking[J]. IEEE Trans Signal Process, 2002, 50(2): 174-88. |