2. 计算智能与智能系统北京市重点实验室, 北京 100124
2. Beijing Key Laboratory of Computational Intelligence and Intelligence System, Beijing 100124, China
DE(differential evolution)算法是由Storn和Price在1995年提出的简单高效的基于群体的随机搜索算法[1],该算法采用实数编码的方式,具有结构简单、易于实现、鲁棒性强等优点,因此,从该算法出现,便吸引了许多相关研究人员的探索[2, 3, 4, 5],并在很多领域取得了成功应用[6, 7, 8]。在研究过程当中,提出了很多种变异策略以适合求解不同的问题。但是,如何根据实际问题选择最恰当的变异策略的过程是很复杂的。Qin和P.N.Suganthan首次提出自适应差分进化策略[9],之后研究者们进行了很多通过自适应选择DE中的变异策略的研究。而差分算法区别其他算法的最大特点就在于其差分变异算子的使用,该算子具有搜索方向和搜索步长自适应的特点。但是,算法对缩放因子F和杂交概率CR的大小设置很敏感,针对不同的问题需要多次运行选择不同的合适经验值。Abbas在文献[10]中提出了自适应调整交叉概率CR的概念,Omran等在文献[11]中提出了一种运用自适应方法调整缩放因子F的算法(self-adaptive differential evolution ,SDE),该算法中的CR是一正态分布数,提高了算法的性能,减少了控制参数,同时用4种标准测试函数测试后,显示出了比其他差分算法更优的表现性能。除了自适应调整CR和F,Teo[12]提出了自适应种群差分算法(exploring dynamic self adaptive populations in DE,DESAP),该算法中群体大小NP也是自适应变化的。上述这些算法的选择策略是唯一的,很难在众多优化问题中进行推广应用。Qin等提出的SaDE算法,采用广义的随机选择方法对每一个目标向量选择变异策略,并跟随着演化代数的变化按规则进行自适应更新[13],CR根据先前的经验值反馈回来进行自适应更新。但是,随着求解问题的复杂度的增加,种群的搜索空间增大,求解难度势必会加大。Rahnamayan为解此问题,提出了基于逆向学习方法的差分进化算法(opposition based DE,ODE)[14],该算法不仅可以应用到种群的初始化过程,而且也可用到进化过程,实现对群体的逆向搜索,大大增强了种群对搜索空间的利用能力。在国内,很多学者针对标准差分算法存在的早熟收敛和搜索停滞等缺陷进行了研究和改进。吴亮红根据群体在运行过程中适应度方差的大小增加了一种新的变异操作,有效提高了算法的全局搜索能力[15]。陈亮提出改进的二进制差分进化算法,改进算法的变异策略的同时,在运行过程中自适应调整种群规模,提高了算法的优化精度[16]。针对算法在解决高维函数优化中存在的缺陷,刘荣辉引入了阶段交叉差分算法,对交叉因子进行自适应控制,提高了算法的收敛精度[17]。Wang将GOBL引入到差分算法中,改进了ODE算法,提出广义逆向学习差分(enhanced opposition-based DE,GODE)算法用来解决高维的函数优化问题,在算法的鲁棒性、收敛速度、成功率等方面均取得了较好的测试效果[18]。
基于以上分析,文中将GOBL应用到SaDE算法中,提出SDE-GOBL算法,用以解决高维优化问题,该算法能够自适应选择变异策略,较好平衡了DE算法的勘测能力与开采能力。并且利用国际上通用的标准测试函数在不同维度下进行验证,结果表明:该算法在解决高维问题时,收敛速度快,寻优精度高,可以推广应用到实际的优化问题中。
1 DE算法差分算法起初主要用于求解实数优化问题,它的最重要的贡献是差分变异算子的引用,该算子主要是针对父代个体,将同一群体中两个不同的个体向量进行差分和缩放操作,再与群体的其他个体向量进行操作得到变异个体向量,根据变异操作方式不同分为不同的变异策略。使之与父个体向量进行杂交形成试验向量,最后让这一试验向量的适应值与父个体向量的适应值进行比较,较优者将保存到下一代。通过以上变异、杂交和选择等操作不断进化,适者生存,一直到满足终止条件停止。算法操作过程如下:
1)编码与初始化
采用实数编码,种群中有NP个个体,自变量有D维,则群体中的第G代第i个个体Xi,G可表示为:Xi,G={xi,G1 xi,G2 … xi,GD},其中,i=1,2,…,NP,xi,G为一实数,且在自变量范围[xmin,xmax]内均匀初始化,此范围针对不同的实际问题进行不同的设置,得到参数优化的定义空间。种群大小NP的取值对算法的收敛也有很大影响,设置较大的值可以增强算法的多样性,但是收敛速度也会降低,过大会造成搜索空间的冗余。
2)差分变异操作
差分算法区别于其他进化算法的地方在于差分变异算子的引用,研究者们用“DE/a/b”的形式表示不同的变异算子,其中“DE”表示差分进化算法,“a”表示基向量的选择方法,包含rand、best、rand-to-best、current-to-best等多种方式,“b”表示变异算子中差分向量的数量。在算法的发展过程中,出现了很多变异策略,其中最有代表性的变异策略包括DE/rand/1、DE/best/1、DE/rand-to-best/1、 DE/best/2、DE/rand/2。由此变异操作产生的变异向量为Vi,G={vi,G1 vi,G2 … vi,GD}。通过控制变异概率F,来完成对差分量的放大和缩小,由此来控制算法的搜索步长的大小。设置的越大,变异向量对后代个体的影响越大,算法收敛越慢。但是过小,又会使种群多样性低,容易出现“早熟”收敛现象。
3)杂交操作
此步操作引入了离散杂交算子,包含二项式杂交和指数杂交方式,把通过变异算子产生的变异向量Vi,G与父向量Xi,G进行离散杂交操作得到试验向量Ui,G</sub>={ui,G1 ui,G2 … ui,GD}。通过二项式杂交算子得到个体的第j(j=1,2,…,D)维个体可标记为式(1):
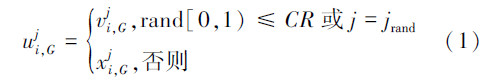
杂交操作是为了增强新种群的离散程度,较大的CR值可以加快算法的收敛,同时其取值与所要求解的问题的特性有关系,当自变量相互独立时,可以设置为[0,0.2],相互依赖强偶合时,可设置成接近于1的数。
4)选择操作
通过初始化、变异、杂交操作产生子代新群体以后,运行此操作步骤。主要是利用一对一贪婪选择的方法将子个体向量与相对应的上一代父个体向量比较,淘汰不良个体,保留优良个体遗传到下一代。通常求解最小化优化问题时,算法的选择操作可表示为

在解决不同的最优化问题时,实验向量采用不同的DE策略进行迭代将产生不同的效果。SaDE算法将不同特性的策略放在一起形成一个候选策略库,在迭代的过程中,根据一定概率pk从策略库中选择一个变异策略,在之前的迭代中越容易达到最优解的DE策略,越容易在此迭代操作中被选择,而不是通过反复实验来找到。然后再进行杂交操作。算法参数的设置如下:
1)初始化选择概率pk为1/4,利用广义随机选择的方法对每一个目标向量选择相应的变异策略并经过LP次(一个学习周期)迭代演化以后,pk值更新为式(3) :

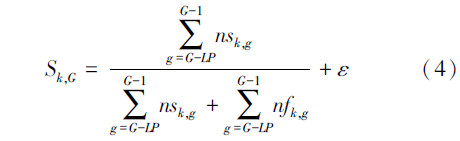
2)每个个体i的缩放因子Fi=rndni(0.5,0.3),是均值为0.5、方差为0.3的正态分布随机数。
3)种群中每个个体选择第k个策略时的杂交概率CRi,k=rndni(CRmk,0.1),如其值不在[0, 1]范围内,则采用截断方法限制在这一范围内,CRmk初始为0.5,CRMemoryk为前LP代中第k个策略产生的子个体成功进入下一代时所保存的CR值,经过LP次迭代以后,每一代CRmk用CRMemoryk中所保存的CR值的中间值代替。
Qin在文献[9]中将该算法与传统DE算法以及另外3种自适应差分算法(ADE、SDE、jDE)通过26个有约束条件的优化测试函数进行了比较,结果表明:SaDE算法在获得最优解时有相对较小标准差和更高的成功率,且收敛速度快。所以文中选择改进后的高性能自适应算法,该算法在解决高维问题时,能以更快的速度达到收敛,满足实际工程的需要。
2.2 基于逆向学习方法的最优化方法逆向学习方法(opposition-based learning,OBL)是智能计算方法中的新兴概念,可以增强各种优化算法的收敛速度。已知候选解Xji,同时计算它的逆向点,这样可以为找到全局最优解提供另一个方法途径。
已知Xij(i=1,2,…,NP,j=1,2,…,D)是一个D维的实数点,NP为种群大小,且Xij∈[aj(G),bj(G)],则点Xji的逆向点可以按照式(5)计算:
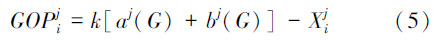
根据概率理论,一个点有50%的可能性比它相应的逆向点获得更好的适应值[19]。这样将广义逆向学习方法应用到差分算法中,可以有效利用群体和逆向群体的信息,提高了对种群的原搜索空间的利用能力,可以在不增大种群搜索空间的前提下,增加找到全局最优解的可能性,有效避免了在解决高维优化问题中算法搜索难度大、操作复杂的问题。
Wang将此方法应用在DE算法中,提出了GODE算法。选用9个高维连续最优化问题[ 20]检验算法的性能,在维数D=50、100、200、500、1 000下,GODE算法比DE、CHC、G-CMA-ES算法运行效果都好,但是在运行F3(shifted rosenbrock's function)、F8(schwefel's problem 1.2)以及F3的混合组成函数F13和F17时,却很难找到最优解。
2.3 基于GOBL的自适应差分算法为有效利用种群有限的搜索空间,降低寻找最优点的难度,将GOBL运用到SaDE这种高效能的自适应DE算法中,能很好地改善算法在解决高维复杂优化问题的收敛性能。采用GOBL初始化种群,如果随机数rand(0,1)满足小于逆向学习概率p0的条件,就运行GOBL更新种群,否则运行SaDE算法中的变异、杂交操作。
一般来说,选择哪种策略放在策略库中是个很严谨的问题。一个好的策略库应在减少一些不必要的策略的同时,仍可以满足不同实际优化问题在种群进化的不同阶段的需要。为了比较的方便,仍选用Qin在SaDE算法中选用的策略库。
策略库中包含4种变异策略:DE/rand/1/bin、DE/rand-to-best/2/bin、DE/rand/2/bin和DE/current -to-rand/1,4种变异策略的公式如 式(6)~(9)所示。其中,DE/rand/1/bin、DE/rand-to-best/2/bin在很多DE算法的改进工作中频繁使用,是比较经典的两种变异策略;DE/rand/2/bin由于加上了高斯扰动使算法具有很好的探测能力;DE/current- to-rand/1可以更有效地解决多目标函数优化问题。 DE/rand/1/bin:
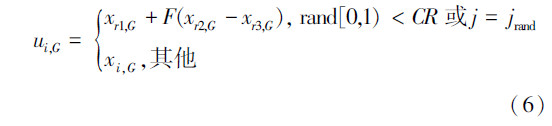
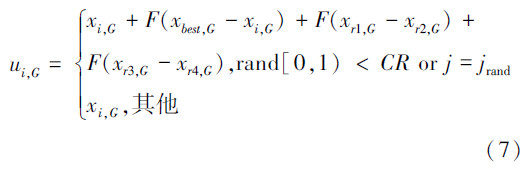

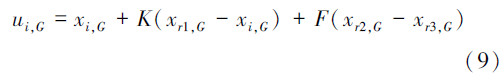
综上所述,SDE-GOBL算法的具体流程如图 1所示。
 |
| 图 1 SDE-GOBL算法流程Fig. 1 The flow chart of SDE-GOBL algorithm |
为检验文中提出的算法的有效性,采用CEC2005国际竞赛所提供的前9个标准测试函数,这9个测试函数多次用来测试算法的性能,具有不同的特性,可抽象的表示实际生活的不同问题。
F1.Shifted Sphere Function;
F2: Shifted Schwefels Problem 1.2;
F3: Shifted Rotated High Conditioned Elliptic Function;
F4: Shifted Schwefels Problem 1.2 with Noise in Fitness;
F5: Schwefels Problem 2.6 with Global Optimum on Bounds;
F6: Shifted Rosenbrocks Function;
F7: Shifted Rotated Griewanks Function without Bounds;
F8: Shifted Rotated Ackleys Function with Global Optimum on Bounds;
F9: Shifted Rastrigins Function.
每一个测试函数具有不同的特征,分别抽象地描述了现实生活的不同问题,其中函数F1~F5是单峰函数,函数F6~F9是多峰函数且极值点的个数非常多,所有的测试函数的最优解皆为0。各个测试函数的详细介绍可参照文献[20]。
以上9个函数都进行了中心偏移旋转,最优值不在原点,不能采用输出结果接近于0的程度作为评价指标,只能采用输出结果与正确结果之间的距离来比较算法的优劣性,这样做是为防止某些算法倾向于优化那些最小值在原点处的函数[16]。因此文中采用解误差测度法评价各个算法的性能,即理想的输出结果与实际输出结果之间的误差距离,定义Derror=f(x)-f(x*),其中,x是算法找寻到的最优解,x*则是目标函数f(x)的已知全局最优解。
3.2 结果分析SDE-GOBL算法与SaDE算法都是参数自适应差分进化算法,交叉因子F和缩放因子CR在算法运行时自动生成并且调整,为进行公平比较,将两个算法的运行条件设置相同,分别设置维数D=30、50(高维),种群大小NP=50,最大评价次数为10 000×D,独立运行2种算法20次,得到测试函数最优值之和。
1)收敛速度
用MATLAB运行测试函数后,得到仿真图如图 2~10,记录找到最优点的迭代次数(如表 1所示)。由此可知,SDE-GOBL算法的收敛速度明显高于SaDE算法,特别是在算法收敛初期表现尤为明显。
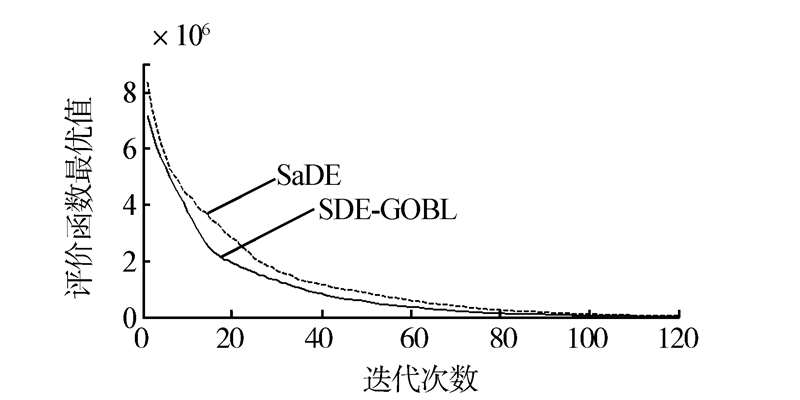 |
| 图 2 F1函数的收敛曲线比较Fig. 2 Convergence curves' comparison of F1 |
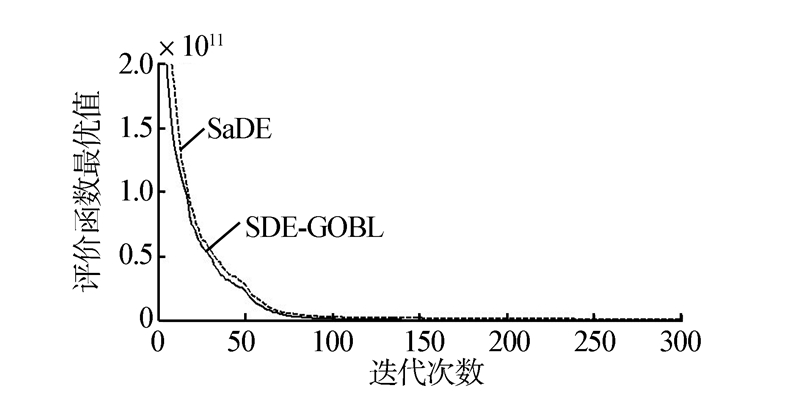 |
| 图 3 F2函数的收敛曲线比较Fig. 3 Convergence curves' comparison of F2 |
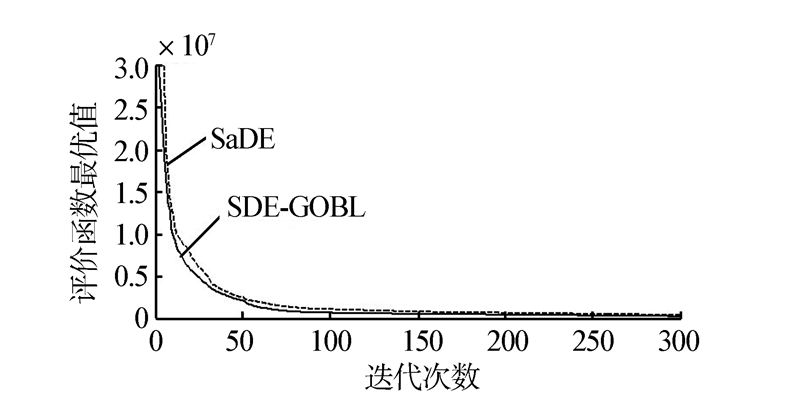 |
| 图 4 F3函数的收敛曲线比较Fig. 4 Convergence curves' comparison of F3 |
 |
| 图 5 F4函数的收敛曲线比较Fig. 5 Convergence curves' comparison of F4 |
 |
| 图 6 F5函数的收敛曲线比较Fig. 6 Convergence curves' comparison of F5 |
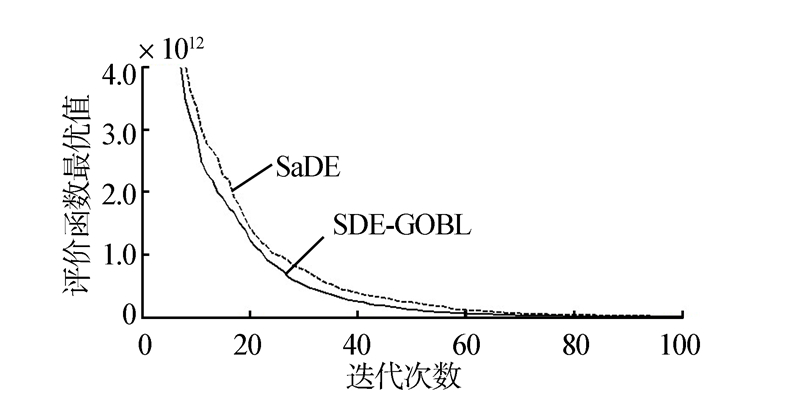 |
| 图 7 F6函数的收敛曲线比较Fig. 7 Convergence curves comparison of F6 |
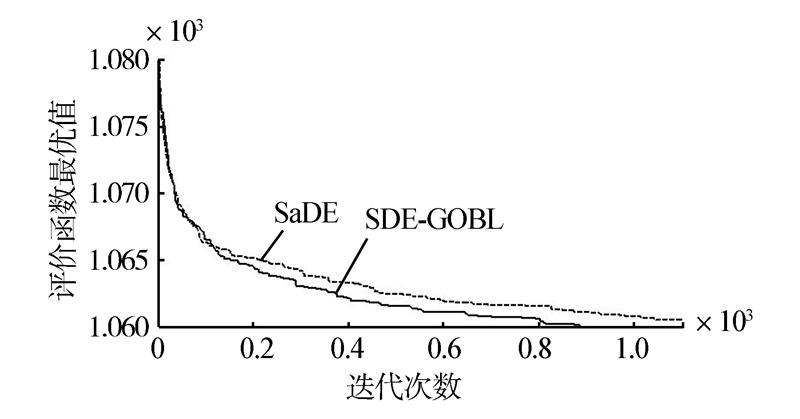 |
| 图 8 F7函数的收敛曲线比较Fig. 8 Convergence curves' comparison of F7 |
 |
| 图 9 F8函数的收敛曲线比较Fig. 9 Convergence curves' comparison of F8 |
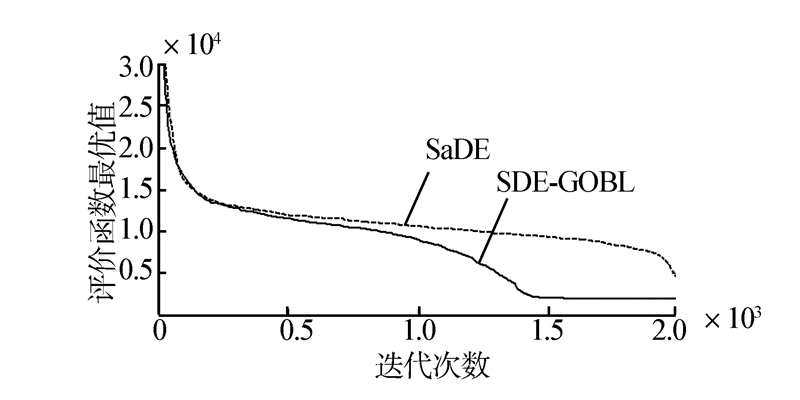 |
| 图 10 F9函数的收敛曲线比较Fig. 10 Convergence curves' comparison of F9 |
| Fun | F1 | F2 | F3 | F4 | F5 |
| SaDE | 120 | 300 | 225 | 110 | 900 |
| SDE-GOBL | 112 | 253 | 171 | 100 | 250 |
| Fun | F6 | F7 | F8 | F9 | |
| SaDE | 90 | 1100 | 1050 | 2000 | |
| SDE-GOBL | 80 | 100 | 900 | 1400 |
2)寻优精度
在D=30和D=50下运行9个测试函数20次,分别记录SaDE算法和SDE-GOBL算法找到最优解的次数 (如表 2所示)。 由表 2可知,除了F7以外,SDE-GOBL算法的寻优精度皆优于SaDE算法。特别是在D=50时,效果更加明显。
| 测试函数 | SDE-GOBL (D=30) | SaDE (D=30) | SDE-GOBL (D=50) | SaDE (D=50) |
| F1 | 17 | 15 | 19 | 16 |
| F2 | 16 | 15 | 18 | 14 |
| F3 | 16 | 15 | 19 | 14 |
| F4 | 17 | 14 | 18 | 13 |
| F5 | 15 | 15 | 18 | 13 |
| F6 | 17 | 15 | 18 | 15 |
| F7 | 14 | 17 | 11 | 18 |
| F8 | 13 | 7 | 16 | 12 |
| F9 | 17 | 13 | 19 | 14 |
DE算法产生早熟收敛的根本原因是随着迭代次数的增加,种群的多样性快速下降 [21]。而在解复杂高维问题时,单纯的增加种群的规模,只会增加算法的运算量,不能从根本上解决早熟收敛问题。文中通过引入逆向学习方法,对算法的初始化种群在进行变异之前进行处理,利用概率论的知识,在不增加种群个数的前提下精炼了初始解,保证了种群的多样性,提高了算法的精度。
对DE算法的3个控制参数:群体大小NP、缩放因子F和杂交概率CR的设置,会对算法的性能产生直接影响,设置不合理将会导致过早收敛或算法停滞。为了弥补此不足,文中采用SaDE算法对参数的设置方法,自适应选择变异策略,各策略根据先前经验值自适应更新CR,使各个策略具有不同的CR,由于GOBL方法的引入,NP的大小不需要再设置在[3D,8D][22],提高了算法的收敛速度。
4 结束语针对一般差分算法在解决高维优化问题时遇到的求解难度大的问题,首次将广义的逆向学习方法应用到多策略自适应差分算法中,有效地解决了传统差分算法求解难度大、运行速度慢且精度低的问题;同时,利用9个标准的测试函数分别在不同高维下展现了算法的优良性能,具有结构简单、容易实现、收敛快速、鲁棒性强等优点,且算法稳定、成功率高。 在该算法中,引入了新的参数p0,这一概率参数的设定是由经验获得,后期可以设计有效的参数自适应策略来更好地解决优化问题,也可以将该算法应用到实际的工程优化问题中,以实现造价低、运行简便等优化目标。
| [1] | STORN R, PRICE K. Differential evolution: a simple and efficient heuristic for global optimization over continuous spaces[J]. Journal of Global Optimization, 1997, 11(4): 341-359. |
| [2] | ALATAS B, AKIN E. MODENAR: multi-objective differential evolution algorithm for mining numeric association rules[J]. Applied Soft Computing, 2008, 8(1):646-656. |
| [3] | DAS S, ABRAHAM A. Automatic clustering using an improved differential evolution algorithm[J].IEEE Trans on Systems Man and Cybernetics, 2008, 38(1): 218-237. |
| [4] | FEOKTISTOV V. Differential evolution: in search of solutions[M]. New York: Springer Verlag, 2006: 205-276. |
| [5] | CHAKRABORTY U. Advances in differential evolution[M]. Berline: Springer Verlag, 2008: 800-805. |
| [6] | QING A. Differential evolution: fundamentals and applications in electrical engineering[M]. IEEE & John Wiley, 2009: 580-590. |
| [7] | QING A, LEE C K. Differential evolution in electromagnetics[M]. Berlin: Springer Verlag, 2010:508-530. |
| [8] | ONWUBOLU G C, DAVENDRA D. Differential evolution: a handbook for global permutation-based combinatorial optimization[M]. Berlin: Springer Verlag, 2009: 301-320. |
| [9] | QIN A K, SUGANTHAN P N. Self-adaptive differential evolution algorithm for numerical optimization[J]. Proc IEEE Congr Evolut Comput, 2005, 2 (2): 1785-1791. |
| [10] | ABBASS H A. The self-adaptive Pareto differential evolution algorithm[J]. Proc Congr Evolut Comput, 2002, 1: 831-836. |
| [11] | OMRAN M G H, SALMAN A, ENGELBRECHT A P. Self-adaptive differential evolution[J]. Lecture Notes in Artificial Intelligence, 2005, 3801: 192-199. |
| [12] | TEO J. Exploring dynamic self-adaptive populations in differential evolution[J]. Soft Comput, 2006, 10 (8): 637-686. |
| [13] | QIN A K, HUANG V L, SUGANTHAN P N. Differential evolution algorithm with strategy adaptation for global numerical optimization[J]. IEEE Trans Evolut Comput, 2009, 13(2): 398-417. |
| [14] | RAHNAMAYAN S, TIZHOOSH H R, SALAMA M M A. Opposition based differential evolution[J].IEEE Trans Evolut Comput, 2008, 12(1): 64-79. |
| [15] | 吴亮红,王耀南,袁小芳.自适应二次变异差分进化算法[J].控制与决策, 2006, 21(8): 898-902.WU Lianghong, WANG Yaonan, YUAN Xiaofang. Differential evolution algorithm with adaptive second mutation[J].Control and Decision, 2006, 21(8): 898- 902. |
| [16] | 陈亮.改进自适应差分算法及其应用研究[D]. 上海:东华大学,2012:39-40.CHEN Liang. Improved adaptive differential evolution algorithm and its applications[D]. Shanghai: Donghua University, 2010: 39-40. |
| [17] | 刘荣辉. 多阶段自适应差分进化算法及应用研究[D].上海:东华大学, 2012: 23-29.LIU Ronghui. Multi-stage self-adapting differential evolution algorithm and its application[D].Shanghai: Donghua University, 2010: 39-40. |
| [18] | WANG Hui, WU Zhijian, RAHNAMAYAN S. Enha nced opposition-based differential evolution for solving high-dimensional continuous optimization problems[J]. Soft Comput, 2010, 15(11): 2127-2140. |
| [19] | RAHNAMAYAN S, TIZHOOSH H R, SALAMA M M A. Opposition versus randomness in soft computing techniques[J]. Soft Comput, 2008, 8(2): 906-918. |
| [20] | SUGANTHAN P N, HANSEN N, LIANG J J, et al. Problem definitions and evaluation criteria for the CEC 2005 special session on real-parameter optimization[J]. KanGAL Report, 2005, 2005005. |
| [21] | 贾丽媛,张弛.自适应差分演化进化算法[J].中南大学学报:自然科学版, 2013, 44(9): 3759-3765.JIA Liyuan, ZHANG Chi. Self-adaptive differential evolution[J]. Journal of Central South University: Science and Technology, 2013, 44(9): 3759-3765. |
| [22] | GäMPERLE R, MüLLER S D, KOUMOUTSAKOS P. A parameter study for differential evolution[J]. Advances in Intelligent Systems, Fuzzy Systems, Evolutionary Computation, 2002, 10: 293-298. |



