2. 大连科技学院 电气工程系, 辽宁 大连 116052
2. Department of Electrical Engineering, Dalian Institute of Science and Technology, Dalian 116052, China
引随着网络控制系统(networked control systems,NCS)应用领域的不断拓展,有关NCS控制理论与应用技术的研究已经引起国内外专家学者的广泛关注。在NCS存在的诸多问题中,时延和数据包丢失一直是影响系统性能质量QoP(quality of performance)的主要因素。无论时延呈现恒定的、随机的、周期的,还是呈现不确定或马尔可夫等特性,时延总会影响系统的稳定性,使系统的稳定范围变窄,在一定条件下甚至使系统失稳,消除时延、减少时延对系统的影响始终是系统控制的目标[1, 2, 3, 4, 5]。对于数据包丢失,却存在主动丢包和被动丢包2种情况:在工业实时控制系统中,为保证信号的及时更新和采样数据的有效性,往往需要主动丢弃一定时间内未到达目标节点的数据包,及时发送和接收新数据,这种主动丢包策略有助于提高系统的实时性;在NCS的网络通信中,由于网络通信机制和带宽资源受限等因素的影响,节点竞争通信中往往出现数据包丢失,这种被动的数据包丢失会加剧系统的通信时延,进一步降低系统的控制性能,改变闭环系统的特性结构。大量的研究成果表明:时延和被动的数据包丢失不仅使系统的结构特性发生改变,影响系统的稳定性和控制性能,而且使系统丧失定常性、完整性、因果性和确定性,研究NCS的时延、丢包补偿与控制方法是非常必要的。然而,现有的许多有关时延和数据包丢失的NCS研究成果[6, 7, 8, 9, 10, 11],其被控对象大多是线性、非线性正常系统。随着NCS应用领域的不断扩大,被控对象为奇异系统的奇异网络控制系统(singular networked control system,SNCS)的控制问题亟待研究。SNCS既包含了NCS的网络通信不确定性,又包含奇异系统本身的结构不确定性和脉冲响应等特性,是具有挑战性的研究课题,近年来已经引起专家学者的广泛关注[12, 13, 14, 15, 16],其中,文献[12]研究了网络环境下时滞广义系统H∞控制器设计问题,给出了系统正则、稳定、无脉冲的条件,获得了具有较小保守性的H∞性能指标;文献[13]和文献[14]研究的是奇异网络控制系统的稳定性条件问题;文献[15]研究了短时延奇异网络控制系统的H∞控制问题,但考虑的是传感器和执行器时钟驱动、控制器事件驱动情况,且没有考虑数据包丢失问题;文献[16]考虑传感器时钟驱动、控制器和执行器事件驱动情况下,研究了奇异网络控制系统的H∞控制问题,但没有考虑数据包丢失情况;同时具有时延和数据包丢失的SNCS的H∞控制研究还鲜见报道。
文中针对传感器时钟驱动、控制器和执行器事件驱动的SNCS,同时考虑时延、数据包丢失和外部输入扰动等因素,研究状态反馈方式下该类系统的H∞控制器设计和优化控制方法问题,给出H∞控制器和优化控制器设计方法和扰动衰减度的求解方法,并通过系统仿真实例说明研究成果的有效性和可行性。
1 问题描述与分析在NCS中,通信网络的带宽由系统各节点所共享。当传感器、控制器和执行器通过网络传输数据时,可能会出现节点竞争失败、网络拥塞、网络瞬间连接中断等情况,使得节点接收数据不完整、数据出错、数据包在一定时间内未达到目标节点,通常将这种情况称为数据包丢失。例如,在采用CSMA/CD协议的以太网中,发生竞争冲突的系统节点将按照二进制指数退避算法BEB(binary exponential backoff)等待一定时间再监听网络是否空闲,在尝试16次监听仍有冲突后,节点将放弃传输,并发出传输失败报告,这导致了随机时延和数据包丢失的发生。 图 1所示的SNCS中,被控对象是具有脉冲特征的奇异系统,w为输入外部扰动,x为测量状态,u为控制输入,z是期望输出。测量传感器时钟驱动,按恒定周期采样被控对象的状态,得到的测量数据通过网络传输给控制器节点。控制器接收到传感测量数据后立即进行控制计算,并发送给执行器节点。执行器接收到控制信号后立即进行调节操作。当整个闭环回路的网络诱导时延不超过一个采样周期T时,传感器到控制器的时延可以并入控制器与执行器一端,记为τ。系统的控制目标是保证系统稳定运行,对于外部扰动w,系统期望输出z尽可能不受影响或非常小。
 |
| 图 1 SNCS一般结构Fig. 1 The general structure of SNCS |
对于该系统,当数据接收节点出现数据包丢失时,该节点仍然使用前一时刻的值,新数据包到达取代过期数据被节点采用。这样,一个存在数据包丢失的网络可以视为按一定速率切换的开关K,因此,存在时延、数据包丢失、输入扰动的SNCS结构如图 2所示。
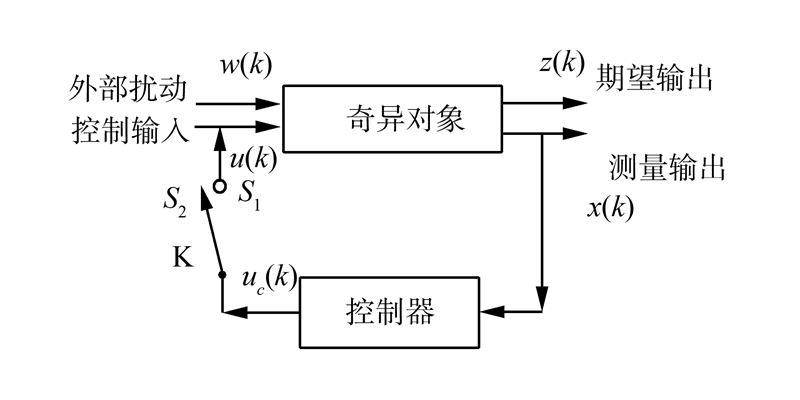 |
| 图 2 具有数据包丢失的 SNCS 结构Fig. 2 The structure of SNCS with data packet dropout |
当无数据包丢失时,网络视为接通,开关K指向S1端,第k周期u(k)=uc(k);当有数据包丢失时,网络视为断开,开关K指向S2端,u(k)=u(k-1)。
奇异被控对象模型描述为式(1):

为分析方便,做合理假设如下:
1)奇异被控对象全部状态可测,通过调整系统局部结构配置使得系统正则,且满足下面条件之一:
(1)degdet(sE-A)=rank(E),(degdet(·)表示行列式的次数,rank(·)表示秩;
(2)
(3)对于可逆矩阵 ,受限等价变换式
,受限等价变换式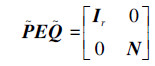 中,N=0。
中,N=0。
2)传感器时钟驱动,控制器和执行器事件驱动。
3)整个闭合回路的网络诱导时延τ小于等于一个采样周期。
4) 网络信息单包传输,且无时序错乱,数据包丢失率是确定的。
5) 系统外部扰动为有限能量,即从w(k)到z(k)的闭环传递函数T(z)满足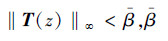 是标量。
是标量。
根据假设条件(1),选择可逆矩阵 ,使得下面的表达式成立:
,使得下面的表达式成立:
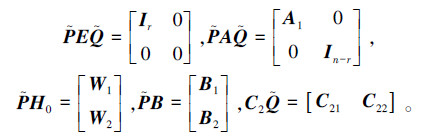
令 被控对象式(1)可以等效变换为式(2):
被控对象式(1)可以等效变换为式(2):
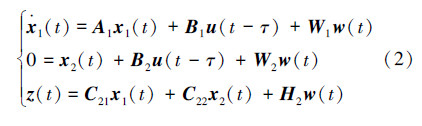
根据假设条件(2)~(4),当网络诱导时延τ≤T时,在一个周期内控制输入u的量值描述是分段连续的,因此被控系统的离散化形式为式(3):
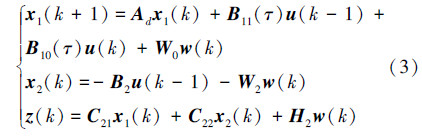
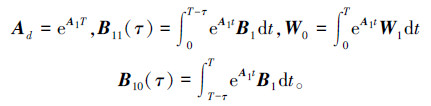
因被控对象全部状态可测,采用状态反馈控制,其控制器模型表示为式(4):
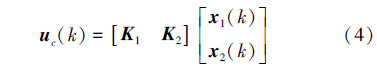
当无数据包丢失时,u(k)=uc(k),联立式(3)和式(4),得到:
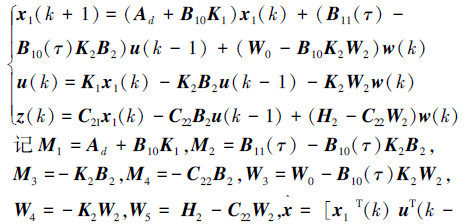
 记
记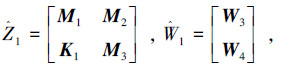
无数据包丢失时,状态反馈SNCS闭环模型为式(5):
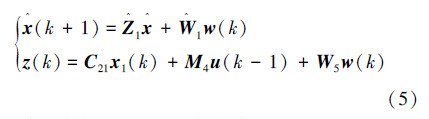
当有数据包丢失时,考虑式(3)和u(k)=u(k-1),并记M5=B10(τ)+B11(τ),可以得到:
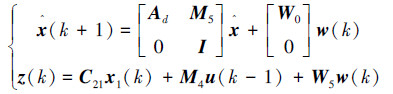 记
记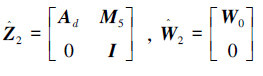
有数据包丢失时,状态反馈SNCS闭环模型为式(6):
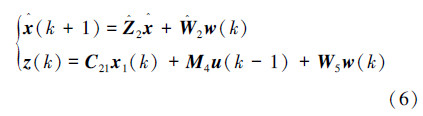
综上2种情况,同时存在时延、数据包丢失和外部扰动的状态反馈SNCS闭环模型表示为式(7):
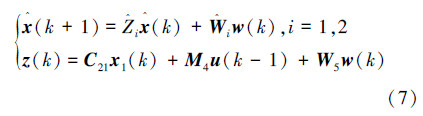
注1 当i=1时,无数据包丢失,i=2时,有数据包丢失,闭环系统的特性矩阵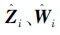 随i值而变化。
随i值而变化。
注2 将闭环系统特性矩阵随数据包丢失动态切换结构的比率,定义为结构事件率,记为 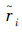 ,i=1,2,对应无数据包丢失的结构事件率为
,i=1,2,对应无数据包丢失的结构事件率为 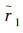 ,对应有数据包丢失的结构事件率为
,对应有数据包丢失的结构事件率为  满足关系
满足关系 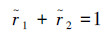 。
。
注3 将网络数据包丢失率记为r,当0<r<1时,结构事件率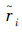 与数据包丢失率r之间满足关系:
与数据包丢失率r之间满足关系: 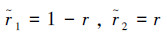 ,因此,有
,因此,有 
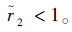 。
。
由此得到结论:当数据包丢失率r一定时,具有时延、数据包丢失和外部扰动的状态反馈SNCS闭环系统模型是由数据包丢失率r约束的异步动态切换系统,系统的稳定性和控制性能将由网络诱导时延、数据包丢失率共同决定。
2 H∞控制器设计
H∞控制定义 对于正常数γ,奇异被控对象式(1)通过网络实施状态反馈控制,当网络存在时延和数据包丢失时,其闭环系统指数稳定;在初始条件(x(0)=0)下,外部扰动w(k)和被调输出z(k)满足H∞范数约束条件‖z(k)‖2≤γ‖w(k)‖2,则称奇异被控对象式(1)可实现γ-次优状态反馈H∞控制,系统扰动衰减度为γ,相应的状态反馈控制器称为γ-次优状态反馈H∞控制器;进一步优化求解使γ最小的状态反馈H∞控制器称为γ-最优状态反馈H∞控制器。
引理1[17] 由事件率  约束的异步动态系统
约束的异步动态系统 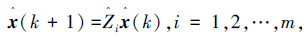 如果存在满足
如果存在满足  的Lypunov函数V(x)及标量α,αi>0,满足条件:
的Lypunov函数V(x)及标量α,αi>0,满足条件:
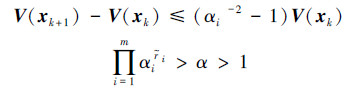
则系统指数稳定,衰减率为 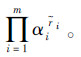
引理2 对于实矩阵W、M、N和F(k),其中,W对称,任意F(k)满足FT(k)F(k)≤I关系,如果不等式W+MF(k)N+NTFT(k)MT < 0,当且仅当存在标量ε>0,使得W+εMMT+ε-1NTN<0。
首先给出具有时延和数据包丢失的状态反馈SNCS指数稳定性条件:
定理1 不考虑系统外部扰动时,对于有时延τ≤T和数据包丢失(丢失率一定且0<r<1)的SNCS系统式(7),如果存在对称正定矩阵 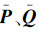 和标量α1>0,α2>0,满足式(8)~(10)的条件:
和标量α1>0,α2>0,满足式(8)~(10)的条件:

则SNCS系统式(7)指数稳定,指数衰减率为α11-rα2r。
证明 对于SNCS闭环模型式(7),根据引理1及结构事件率  和网络数据包丢失率r之间的关系
和网络数据包丢失率r之间的关系  ,可以推知,当满足下面条件时,该系统指数稳定:
,可以推知,当满足下面条件时,该系统指数稳定:
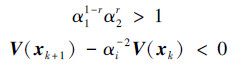 选择正定矩阵S、R,定义满足引理1的Lyapunov函数为式(11):
选择正定矩阵S、R,定义满足引理1的Lyapunov函数为式(11):
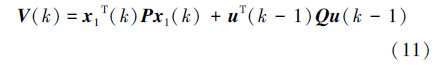
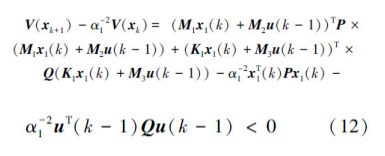
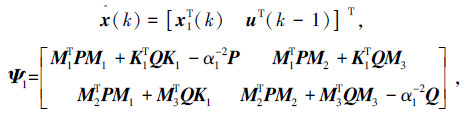
则式(12)可表示为
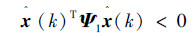 式中:
式中:
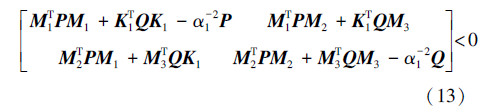
利用Schur补性质,式(13)可以变换为

式(14)两边左乘、右乘diag(P-1,Q-1,I,I),得
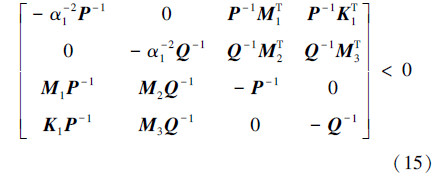
令 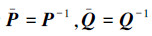 ,则式(15)等价于式(9)
,则式(15)等价于式(9)
当有数据包丢失时,考虑闭环系统式(7)和u(k)=u(k-1),可以得到:
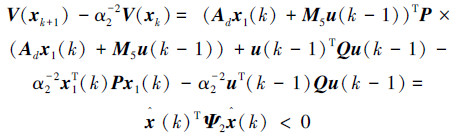 式中:
式中:
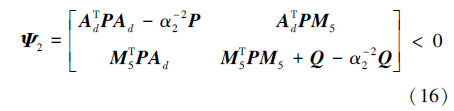
类似地,利用Schur补性质变换式(16),随后式(16)两边左乘、右乘diag(P-1,Q-1,I),同样考虑  ,则式(16)等价于式(10),定理1证毕。
,则式(16)等价于式(10),定理1证毕。
定理2给出H∞控制器存在的条件。
定理2 对于给定的常数γ>0,如果存在对称正定矩阵 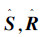 ,标量αi>0,i=1,2,使得式(17)~(19)的条件成立:
,标量αi>0,i=1,2,使得式(17)~(19)的条件成立:

证明 根据H∞控制定义,当‖z(k)‖2≤γ‖w(k)‖2成立时,令
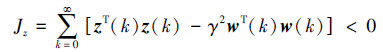 选择Lyapunov函数为
选择Lyapunov函数为
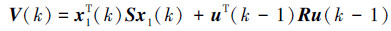
若系统式(7)指数稳定,在零初始条件下,对于∀w(k)∈L2[0,∞),有:
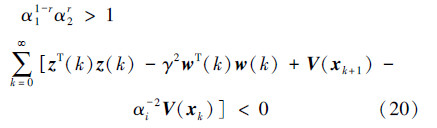
当无数据包丢失时,展开式(20),得到:
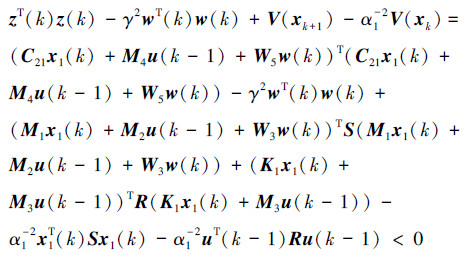 令
令 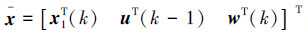 ,式(20)可以表示为
,式(20)可以表示为 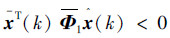 ,其中,Φ的表达式为
,其中,Φ的表达式为

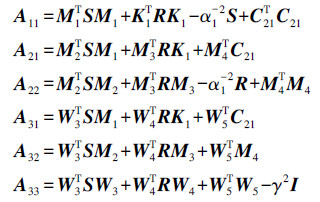 利用Schur补性质,式(21)可变换为
利用Schur补性质,式(21)可变换为

类似地,式(22)进一步变换,即可得到式(18)。
当有数据包丢失时,u(k)=u(k-1),根据式(20)可以表示为
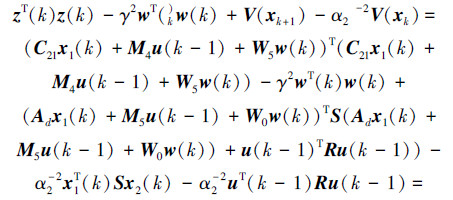
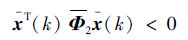 式中:
式中:

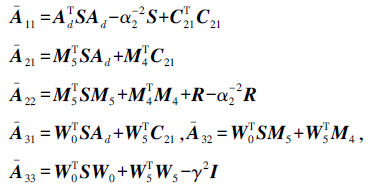
利用Schur补性质,对式(23)做类似变化,即可得到式(19),定理2证毕。
注4 因为具有时延和数据包丢失的奇异网络控制闭环系统模型是由数据包丢失率r约束的异步动态切换系统,其闭环系统模型随着数据包丢失的存在与否在式(6)和式(5)之间切换,在定理1和定理2中,有、无数据包丢失的情况都考虑在内所进行的证明,因此,本文设计的控制器适用于数据包丢失与否的任意情况。
定理3 对于SNCS式(7),如果存在对称正定矩阵 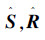 ,矩阵Y1,Y2,Y3,标量ε>0,ε1>0,β>0,α1>0,α2>0,以及相容维数的单位矩阵I,使得式(24)~(26)的矩阵不等成立:
,矩阵Y1,Y2,Y3,标量ε>0,ε1>0,β>0,α1>0,α2>0,以及相容维数的单位矩阵I,使得式(24)~(26)的矩阵不等成立:


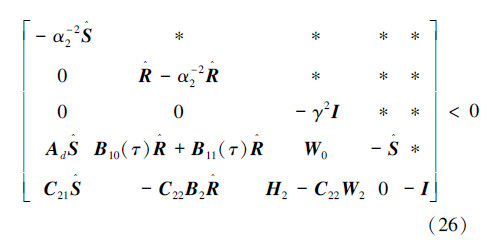
 ,γ-次优状态反馈H∞控制器为
,γ-次优状态反馈H∞控制器为
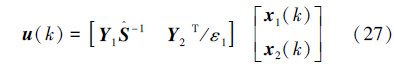
证明 若存在状态反馈H∞控制,根据定理2,展开M1~M4,W3~W5,用符号“*”表示不等式对称项,不等式(18)可表示为
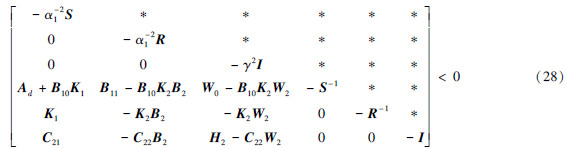
式(28)可以表示为
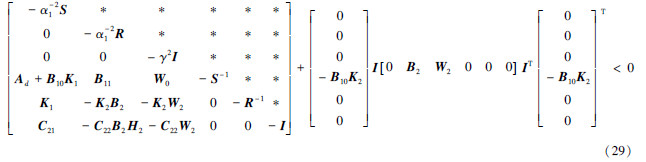
由引理2,式(29)成立,当且仅当存在标量ε>0,使得式(30)成立:

由Schur补性质,式(30)可进一步变换为式(31):
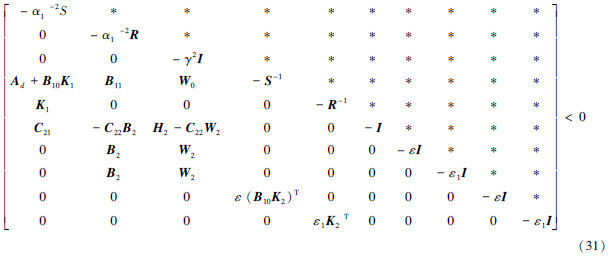
式(31)左、右乘diag(S-1,R-1,I,I,I,I,I,I,I,I),令  ,Y2=ε1K2T,β=γ2,Y3=εK2T,则式(31)等价于式(25)。
,Y2=ε1K2T,β=γ2,Y3=εK2T,则式(31)等价于式(25)。
类似地,式(19)可以表示为
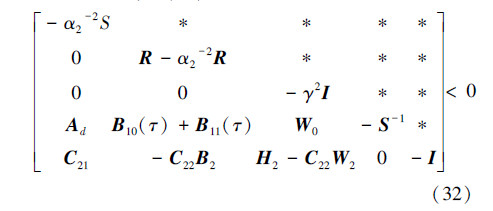
式(32)左、右乘diag(S-1,R-1,I,I,I),并且令 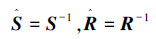 ,式(32)即可变换为式(26)。
,式(32)即可变换为式(26)。
γ-次优状态反馈H∞控制器参数为
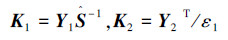 由此得到γ-次优状态反馈H∞控制器式(27),扰动衰减度为
由此得到γ-次优状态反馈H∞控制器式(27),扰动衰减度为 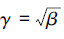 ,证毕。
,证毕。
定理4 对于SNCS 式(7),如果式(33)优化问题有可行解:
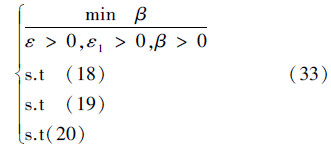
则γ-最优状态反馈H∞控制器为式(34):
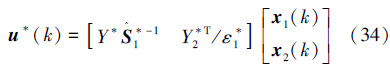
最小扰动衰减度为 
注5 利用MATLAB工具箱LMI中的可行性问题求解器feasp求解定理2,如果有可行解,证明系统可以实现H∞控制,进一步求定理3的可行解,即可得到γ-次优状态反馈H∞控制器参数和扰动衰减度;用优化问题求解器mincx求解定理4的优化解,可以得到γ-最优状态反馈H∞控制器参数和最小扰动衰减度。
3 仿真实例
选择奇异被控对象模型为
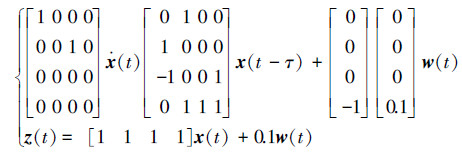
通过网络实施状态反馈H∞控制,传感器测量周期为0.1 s,网络诱导时延τk=0.01 s,数据包丢失率为0.05。
选择非奇异矩阵:
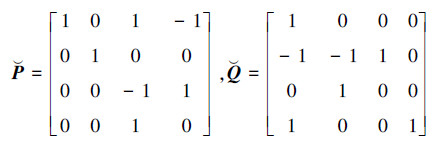
奇异被控对象可等价变换为
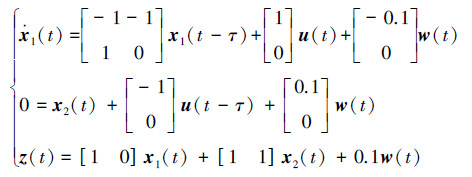
其离散化系统为

可求得:

通过H∞控制,应用定理3,选择标量α1=1.026 1>0,α2=0.707 9>0,得到可行解为α11-rα2r 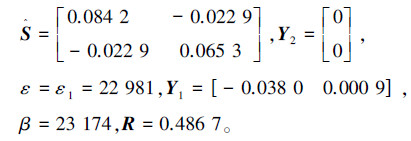
该系统指数稳定,指数衰减度为1.033 6,H∞扰动衰减度为 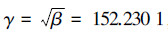 ,γ-次优状态反馈H∞控制器为u(t)=-0.495 3-0.159 3 0 0x(t)。
,γ-次优状态反馈H∞控制器为u(t)=-0.495 3-0.159 3 0 0x(t)。
在H∞控制器u(t)作用下,初始状态为(0,2,1,-1)时系统状态响应曲线如图 3虚线所示,其中,图 3(a)为状态x1(t)分量响应,图 3(b)为状态x2(t)分量响应,图 3(c)为状态x3(t)分量响应,图 3(d)为状态x4(t)分量响应,由图可以看出,系统内部状态是稳定的。在u(t)作用下该系统期望输出z的响应曲线如图 4(a)所示,可以看出该系统也是外部稳定的,曲线中的尖峰毛刺是外部扰动引起的。
利用LMI工具箱的mincx进行优化求解,应用定理4得到相应解为
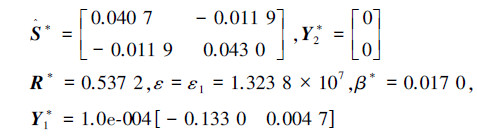
H∞扰动最小衰减度为 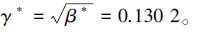
γ-最优状态反馈H∞控制器为 u*(t)=[-1.201 7-0.291 400]x(t)
在优化控制器u*(t)作用下,同样初始状态(0,2,1,-1)时,优化后的系统状态各分量响应曲线如图 3实线所示,优化后系统期望输出z响应曲线如图 4(b)所示。
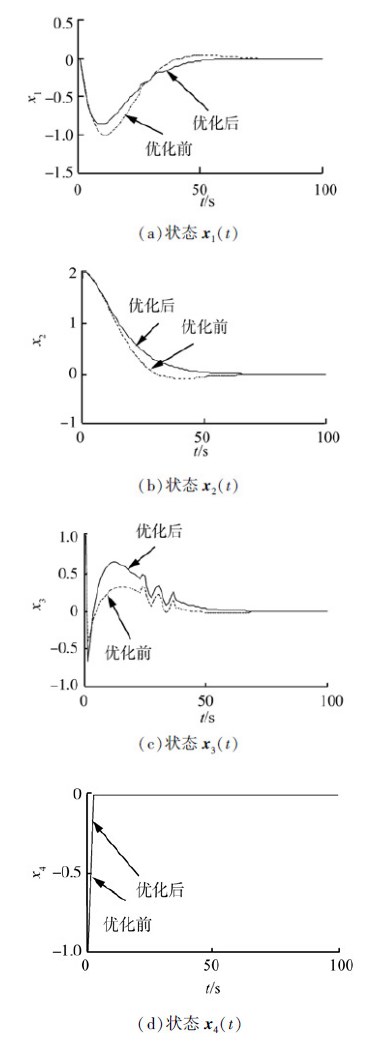 |
| 图 3 H∞控制状态响应Fig. 3 H∞ control state |
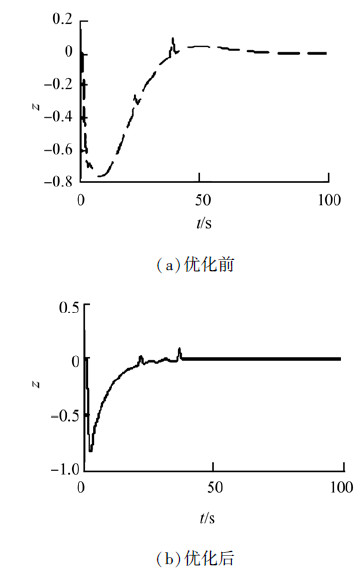 |
| 图 4 H∞控制期望输出响应Fig. 4 H∞ control output response |
仿真结果表明,实施H∞控制,系统不仅指数稳定,经控制器优化,状态分量与期望输出的震荡幅度、调节时间和尖峰毛刺明显减小,扰动衰减度从152.230 1减小到0.130 2,抗扰性能得到明显增强,期望输出的平稳性明显得到改善。
4 结束语奇异系统广泛存在于电网电路、电力传输、投入产出规划、神经网络等系统中,开展奇异网络控制系统理论与方法的研究,对建立奇异网络控制系统理论体系具有重要意义。文中针对具有时延、数据包丢失和外部扰动的奇异网络控制系统,当测量传感器时钟驱动、控制器和执行器事件驱动、网络诱导时延不超过一个采样周期、数据包丢失率一定、外部扰动为有限能量等条件下,给出了奇异网络控制系统状态反馈H∞控制器设计方法和相应扰动衰减度求解方法,成果具有普遍意义。仿真结果表明经H∞优化控制后,系统的平稳性得到明显改善,扰动衰减度大大减小,也验证了分析方法和结果的有效性和可行性。
| [1] | ZHANG W A, YU L. A Robust control approach to stabilization of networked control systems with short time-varying delays [J]. Acta Automatica Sinica, 2010, 36(1):87-91. |
| [2] | 田中大,高宪文,李琨. 基于预测控制的NCS时延补偿算法 [J]. 系统工程与电子技术, 2013, 35(10): 2165- 2169.TIAN Zhongda, GAO Xianwen, LI Kun. Networked control system time-delay compensation algorithm based on predictive control [J]. Journal of Systems Engineering and Electronics, 2013, 35(10): 2165-2169. |
| [3] | 李同涛,邓丽,费敏锐,等.一类带有随机、有界时滞网络控制系统的脉冲控制[J]. 控制与决策, 2013, 28(2): 294-298.LI Tongtao, DENG Li, FEI Minrui, et al. Networked control systems with bounded random time delay based on impulsive control [J]. Control and Decision, 2013, 28(2): 294-298. |
| [4] | LI Yuan,ZHANG Qingling, QIU Zhanzhi. Stability of networked control systems with time-varying sampling periods and partially known transition probabilities[J]. International Journal of Information & Systems Sciences, 2012, 7(4):340-356. |
| [5] | 游科友,谢立华.网络控制系统的最新研究综述 [J]. 自动化学报, 2013, 39(2): 101-118.YOU Keyou, XIE Lihua. Survey of recent progress in networked control systems [J]. Acta Automatica Sinica, 2013, 39(2):101-118. |
| [6] | SUN Y G, QIN S Y. Stability and stabilization of networked control systems with bounded packet dropout [J]. Acta Automatica Sinica, 2011, 37(1): 113-117. |
| [7] | 严怀成,苏阵阵,张皓,等.具有时变时滞和多包丢失的网络控制系统量化∞控制[J]. 控制理论与应用, 2013,30(4): 469-474.YAN Huaicheng, SU Zhenzhen, ZHANG Hao, et al. Quantized H-infinity control for networked control systems with time-varying delay and multiple packet dropouts [J]. Control Theory & Applications, 2013, 30(4): 469-474. |
| [8] | YANG R N, SHI P, LIU G P, et al. Network-based feedback control for systems with mixed delays based on quantization and dropout compensation [J]. Automatica, 2011, 47(12): 2805-2809. |
| [9] | LI J N, YU H B, YUAN D C, et al. Co-design of networks and control systems with synthesized controller [J]. InternationaL Journal of Information and Systems Sciences, 2011,7(1): 131-140. |
| [10] | LIU M, CAO X B, SHI P. Fuzzy-model-based fault-tolerant design for nonlinear stochastic systems against simultaneous sensor and actuator faults [J]. IEEE Transactions on Fuzzy Systems, 2013, 21(5): 789-799. |
| [11] | 李媛, 张庆灵, 邱占芝等. 具有时变采样周期网络控制系统的严格耗散控制[J].控制理论与应用, 2013, 30(9): 1170-1177.LI Yuan, ZHANG Qingling, QIU Zhanzhi, et al. Strictly dissipative control for networked control systems with time-varying sampling periods [J]. Control Theory & Applications, 2013, 30(9): 1170-1177. |
| [12] | 杨帆,邱占芝,周世玉. 网络环境下时滞广义系统∞控制器设计[C]//第31届中国控制会议论文集. 合肥,中国, 2012:5933-5937.YANG Fan, QIU Zhanzhi, ZHOU Shiyu. The designing of H-infinite contrlller for the singular networked control systems with time-delay[C]//Proceedings of the 31st Chinese Control Conference. Hefei, China, 2012: 5933- 5937. |
| [13] | FENG Y F, ZHU X L, ZHANG Q L. Delay-dependent stability criteria for singular time-delay systems[J]. Acta Automatica Sinica, 2010, 36(3): 433-437. |
| [14] | QIU Z Z, ZHANG Q L, ZHAO Z W. Stability of singular networked control systems with control constraint[J]. Journal of Systems Engineering and Electronics, 2007,18(2): 290-296. |
| [15] | 王燕锋, 井元伟, 张嗣瀛,等. 一类短时延的广义网络控制系统的鲁棒∞控制 [J]. 东北大学学报:自然科学版, 2011, 32(5): 609-613.WANG Yanfeng, JING Yuanwei, ZHANG Siying, et al. Robust ∞ control for a kind of singular networked control system with short time delay [J]. Journal of Northeastern University:Natural Science, 2011, 32(5): 609-613. |
| [16] | QIU Z Z, SHI L. H-Infinite controller design of singular networked control systems [J]. Intelligent Control and Automation, 2014(5): 24-34. |
| [17] | RABELLO A, BHAYA A. Stability of asynchronous dynamical systems with rate constraints and applications [J]. IEE Proceedings: Control Theory and Applications, 2003,150: 546-550. |



