2. 南京财经大学 江苏省粮油品质控制及深加工技术重点实验室, 江苏 南京 210046;
3. 南京林业大学 江苏省制浆造纸科学技术重点实验室, 江苏 南京 210037
2. Jiangsu Key Laboratory of Quality Control and Further Processing of Cereals and Oils, Nanjing University of Finance Economics, Nanjing 210046, China;
3. Jiangsu Provincial Key Laboratory of Pulp and Paper Science and Technology, Nanjing Forestry University, Nanjing 210037, China
图像分割是图像处理与识别的前期关键技术之一。阈值分割因简单实用而成为常用的图像分割方法,可广泛应用于储粮害虫、纸病等一系列机器视觉检测领域。其关键是快速得到最佳阈值,以此分离图像中的目标和背景。人们已提出了大量的阈值分割方法[1, 2, 3, 4, 5],其中Kapur等[4]提出的最大Shannon熵阈值选取方法受到广泛关注。Abutaleb[5]将最大Shannon熵法从一维拓展到了二维,对含噪图像的分割效果相较一维方法有明显的改善,但使得计算量大幅增加,实时处理能力较差。为此,提出了二维最大熵法的快速算法[6, 7]。为了进一步提高运算速度,Du等[8]给出了粒子群算法优化的二维最大Shannon熵方法,大大加快了二维算法的处理速度。Li等[9]对一维最大Shannon熵法进行扩展,提出了一维最小交叉熵法,取得不错的分割效果。同样为了弥补一维方法抗噪性的不足,雷博等[10]将一维最小交叉熵法推广到二维。文献[11]应用混沌弹性粒子群算法,更好地解决了二维Shannon交叉熵方法的实时性问题。但是Shannon熵及Shannon交叉熵均存在概率为零处无意义的缺陷。为了更好地衡量图像的不确定性,Sahoo将统计力学中的Tsallis熵引入到图像分割中,提出了二维Tsallis 熵阈值分割方法[12]。Tsallis熵不仅能够刻画任意概率的信息量,而且引入了参数q描述系统的非可加性程度,能较好地考虑图像中目标和背景的相互关系,具有灵活性和普适性。但二维Tsallis 熵阈值分割方法依然存在运算速度过慢的问题。为此,文献[13]采用粒子群优化算法进行加速。文献[14]则将 Tsallis 熵法扩展到Tsallis交叉熵法,给出了基于混沌粒子群优化的二维对称Tsallis交叉熵阈值分割方法。其考虑了图像类内灰度均匀性,更准确地表征了图像分割前后信息量差异。但是二维对称Tsallis交叉熵阈值选取公式相对繁长,影响了算法的运算效率。若能寻求简洁的Tsallis交叉熵公式来度量图像信息量变化,并注意灵活选取参数q,有望在保证分割效果的基础上,加快运行速度。
上述4种二维熵阈值选取方法(包括二维最大Shannon熵法、二维Shannon交叉熵法、二维Tsallis熵法和二维对称Tsallis交叉熵法)还存在一个共同的问题:将二维直方图直分成4个区域后,计算熵值时只考虑对角线上的2个矩形区域,忽略了其他区域中属于目标和背景的有用信息[15]。因此,这种处理方法导致分割结果不够准确。此外,上述4种方法所采用的粒子群算法容易陷入局部极值的束缚,难以保证收敛到最佳阈值,算法遍历性有待提高。而近年来提出的人工蜂群算法具有收敛速度快、避免局部极值问题等优点。
鉴于以上分析,文中提出一种蜂群优化的二维非对称Tsallis交叉熵阈值分割方法。首先给出二维非对称Tsallis交叉熵的定义,并在二维直方图区域划分基础上,提出二维非对称Tsallis交叉熵的阈值选取方法;然后采用蜂群算法搜寻最佳阈值;最后将实验结果与基于粒子群优化的二维最大Shannon熵法[9]、二维Shannon交叉熵法[12]、二维Tsallis熵法[13]、二维对称Tsallis交叉熵法[14]的分割结果及运行时间进行比较。
1 非对称Tsallis交叉熵的定义非对称Tsallis交叉熵可在Tsallis熵的基础上定义。设任意2个概率分布P={p1,p2,...,pN}和Q={q1,q2,…,qN},N≥1,满足条件pi≥0,qi≥0,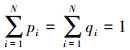 ,则P和Q之间的非对称Tsallis交叉熵定义为
,则P和Q之间的非对称Tsallis交叉熵定义为

注意到当q无限逼近1时,有
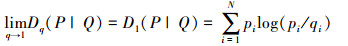
即非对称Tsallis交叉熵Dq(P|Q)转化为非对称Shannon交叉熵D1(P|Q)。式(1)定义的非对称Tsallis交叉熵区别于文献[14]提出的对称Tsallis交叉熵,它同样能够表达系统变换前后的差异,而且表达形式更加简洁。
2 二维非对称Tsallis交叉熵阈值选取方法设大小为M×N、灰度级数目为L的图像中像素点(m,n)的灰度级为f(m,n),g(m,n)为8-邻域平均灰度级。若用(i,j)表示二元对(f(m,n),g(m,n)),i,j=0,1,…,L-1,r(i,j)表示(i,j)出现的频次,则f(m,n)与g(m,n)的联合概率p(i,j)可表示为p(i,j)=r(i,j)/(M·N),且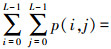 =1。{p(i,j)}即为灰度级—邻域平均灰度级二维直方图。
=1。{p(i,j)}即为灰度级—邻域平均灰度级二维直方图。
二维直方图的传统划分方式如图 1所示。以(t,s)为交点划分为4个区域:区域0为目标(背景),区域1为背景(目标),区域2和3表示边界点和噪声。由于计算熵值时只考虑对角线上的区域0和1两个矩形区域,忽略了区域2和3中属于目标和背景的有用信息,致使分割结果不够准确。为了解决这一问题,将二维直方图按图 2所示进行划分。
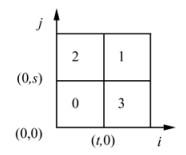 |
| 图 1 传统的直方图区域划分Fig. 1 The original histogram region division |
设二维直方图的整个区域为C,Co与Cb分别表示目标类和背景类,即
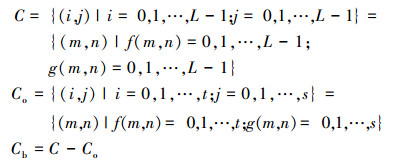
依据图 2可知,该种划分在计算熵值时能尽可能地考虑到图像中目标和背景像素的灰度信息,由此可得到更准确的阈值。
 |
| 图 2 所采用的直方图区域划分Fig. 2 The used histogram region division |
区域Co和区域Cb的先验概率ωoo和ωob分别为
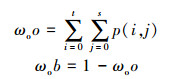
现采用非对称Tsallis交叉熵,表征分割前后图像的信息差异。设分割前后图像的非对称Tsallis交叉熵Df=[Di Dj]T,其中Di和Dj分别表示分割前后图像在i方向和j方向上的交叉熵。下面首先给出Di的推导过程,类似可以得到Dj。
图像总的灰度均值uti为

灰度值的总和为
Ui=M·N·uti
设 ,区域Co和区域Cb的灰度均值uio和uib分别为
,区域Co和区域Cb的灰度均值uio和uib分别为
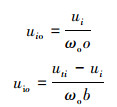
设分割前后图像像素特征矢量的概率分布分别为P=pm,n和Q=qm,n,其中pm,n可用原图像空间中每个像素点的灰度占比表示,即
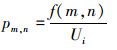
qm,n表征分割后图像空间中每个像素点所属区域的灰度均值占比,即
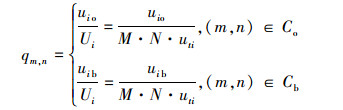
显然pm,n、qm,n都满足非对称Tsallis交叉熵概率分布的条件:pm,n≥0,qm,n≥0, ,
,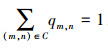 ,从而得到Di:
,从而得到Di:


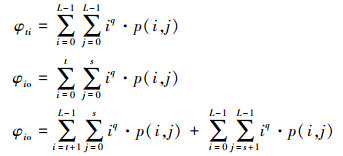

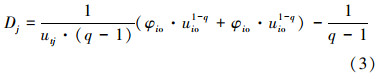
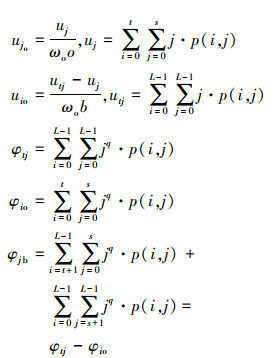
则分割前后图像的非对称Tsallis交叉熵为 Df=[Di Dj]T=
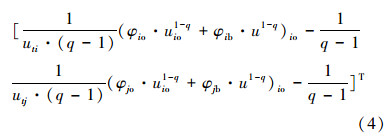
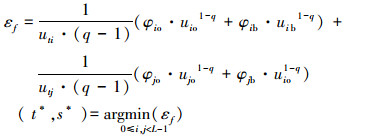
在计算ωoo、ui、uj、φio、φio时,为缩短算法运行时间,减少迭代过程中有关函数的重复计算,可建立如下的查找表:
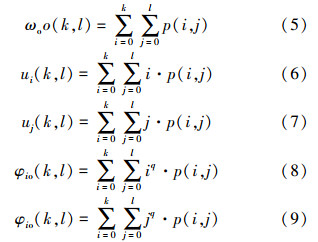
用递推方式计算式(5)~(9)的中间参量,能使复杂度从O(L4)下降到O(L2),从而使算法运行时间大幅减少。递推算法为:
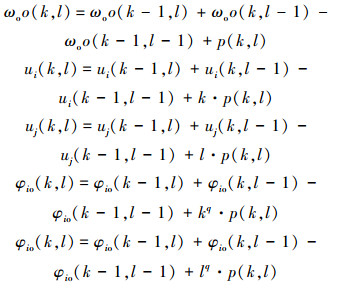
为了加快算法运行速度,可以采用智能优化算法搜寻最佳阈值。由于现有的粒子群算法易陷入局部最优、收敛精度低、算法稳定性不够等不足,文中提出采用蜂群算法搜索最佳阈值,以进一步加快算法搜索速度,提高算法精度和实时性。
3 非对称Tsallis交叉熵阈值选取的人工蜂群优化算法人工蜂群算法(artificial bee colony algorithm,ABC)是受到蜂群采蜜的规律性启发进而建立的简化模型,主要由蜂群分工的3个职能构成:引领、观察、侦查。
1)引领。引领蜂的数目是确定的,设为ML,每一只引领蜂对应一个食物源。食物源位置表示目标函数的可能解,亦即可能的最佳阈值。食物源的花蜜质量由相应解的适应度表示:
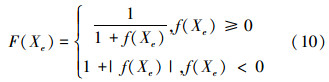
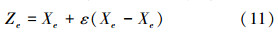
2)观察。通常设置观察蜂的数目与引领蜂相同,也为ML。首先由引领蜂对应食物源的花蜜适应度确定出概率Pe;然后观察蜂以Pe的概率选取该引领蜂跟随。Pe的表达式为
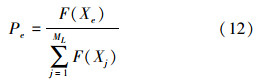
在所跟随的引领蜂对应食物源附近,观察蜂根据式(12)随机搜索一个新食物源。将新旧食物源比较后,引领蜂继续选择较优的食物源。
3)侦查。引领蜂的职能转为侦查自身是否陷入局部极值。如果陷入局部极值,搜索新的位置以便跳出局部极值。
这3个职能循环执行直至搜索到最佳阈值。需要注意的是,将蜂群算法应用于图像阈值选取时,目标函数的自变量是离散值,必须对自变量取整。
二维非对称Tsallis交叉熵阈值选取的蜂群优化算法具体步骤如下:
1)设置算法的控制值,蜜蜂的总数NC设为30,引领蜂和观察蜂各一半。最大循环次数CM定为20。判断引领蜂是否陷入局部极值的循环次数CL设为3。维数D为2。t的搜索范围为[1, 254],s的搜索范围为[1,Ls-2],Ls=max[g(i,j)]。当前的循环次数C为1;
2)初始化引领蜂对应食物源的位置Xe(e=1,2,...,15),Xe是二维量,2个分量分别在t和s的搜索范围之间随机产生,须取为整数。根据式(10)计算每个解的适应度值;
3)按照式(11),每一只引领蜂在食物源附近随机搜寻到一个新解Ze(对Ze取整),然后计算Ze的适应度值,取新旧解的较优值赋给Xe;
4)根据式(12),观察蜂以概率Pe跟随一只引领蜂,根据式(11)在食物源附近随机搜寻一个新整数解,选取新旧解的较优值赋给Xe;
5)如果经过CL次循环,Xe的适应度值没有改善,搜索新的整数解代替Xe,否则程序继续进行;
6)当一次循环结束时,将本次循环的最优解与之前全局最优值比较,决定当前全局最优值,C自动加1;
7)若C达到CM,停止迭代,根据得到的最佳阈值向量分割图像,否则转3)继续迭代。
4 实验结果与分析利用文中提出的蜂群优化的二维非对称Tsallis交叉熵阈值选取方法,对大量不同类型的图像进行了阈值分割实验,发现选取合适的参数q值,图像分割的结果会更加准确。与二维最大Shannon熵法、二维Shannon交叉熵法、二维Tsallis熵法、二维对称Tsallis交叉熵法相比,本文提出的方法在分割质量和运行效率2方面皆有优势。
实验中能否正确选取参数q值对图像分割效果有重要的影响[17]。不同的图像所需选取的最佳q值可能不一样;同一幅图像需要分割出的目标不同,q值可能也要改变。为满足自动化的要求,不可能对每幅图像的q值进行人为设置和调整。基于文中方法,重点对储粮害虫和纸病2类图像做了大量实验,找到了符合这2类图像最为合适的q值。总体来说,分割储粮害虫图像时,q设置为0.01能取得较好效果。纸病图像要视待分割目标所处的灰度级区域区别设置:分割的目标是黑斑等暗灰度级区域时,可设置q=0.01;而分割的目标是孔洞等亮灰度级区域时,可设置q=15。
实验是在Pentium(R) Dual-Core CPU 2.0 GHz、2 GB RAM、MATLAB 7.1环境中进行的。因篇幅有限,分别给出2幅储粮害虫和2幅纸病图像的实验结果及算法运行时间。图 3(a)~图 6(a)为原始灰度图像。其中,图 3(a)与图 4(a)为储粮害虫图像;图 5(a)为低对比度的黑斑纸病图像,图 6(a)为孔洞纸病图像。图 3(b)~图 6(b)为基于粒子群优化的二维最大Shannon熵法的分割结果;图 3(c)~图 6(c)为基于粒子群优化的二维Shannon交叉熵法的分割结果;图 3(d)~图 6(d)为基于粒子群优化的二维Tsallis熵法的分割结果(q=0.8,为该方法理想参数值[13]);图 3(e)~图 6(e)为基于粒子群优化的二维对称Tsallis交叉熵法的分割结果(q=0.8,为该方法理想参数值[18]);图 3(f)~图 6(f)为文中提出方法的阈值分割结果。从图 3到图 6的分割结果可以看出,只有二维对称Tsallis交叉熵法和文中方法能较好地分割出储粮害虫、黑斑、孔洞等目标,其他方法则不能将目标从背景中完全地提取出来。
 |
| 图 3 储粮害虫图像1及其分割结果Fig. 3 Stored-grain pests image 1 and its segmentation results |
 |
| 图 4 储粮害虫图像2及其分割结果Fig. 4 Stored-grain pests image 2 and its segmentation results |
 |
| 图 5 黑斑纸病图像及其分割结果Fig. 5 Black ash spot image and its segmentation results |
 |
| 图 6 孔洞纸病图像及其分割结果Fig. 6 Crater image and its segmentation results |
从图 3~6的分割结果可以看出,只有二维对称Tsallis交叉熵法和文中方法能较好地分割出储粮害虫、黑斑、孔洞等目标,其他方法则不能将目标从背景中完全地提取出来。再进一步分析比较二维对称Tsallis交叉熵法和文中方法的分割结果:图 3(e)不能将储粮害虫目标和与其灰度级相近的粮食颗粒完全分离,而图 3(f)则不存在错分现象,分割出的储粮害虫目标完整清晰;图 4(e)分割出的储粮害虫目标丢失了触须和足节等重要细节特征信息,而图 4(f)分割出的储粮害虫目标触须和足节特征清晰可辨,只是稍有错分斑点,经过后期处理不影响对储粮害虫目标的分类识别工作;图 5(e)和图 5(f)的分割效果相近,但文中方法的错分斑点更少;图 6(e)和图 6(f)都能准确地分割出孔洞目标。现引入区域间对比度对上述5种阈值分割方法进行定量评价。根据分割后图像目标和背景的区域间对比度,可以判别图像分割的质量。区域间对比度越高,分割效果越好。表 1列出了5种方法的区域间对比度。由表 1可以看出,所提出方法得到的区域间对比度均高于另外4种方法。综上可见,文中方法的分割效果相对更优。
表 2列出了5种方法的最佳阈值及运行时间比较。从中可以看出,与其他基于粒子群优化的阈值分割方法相比,本文提出的基于蜂群优化的二维非对称Tsallis交叉熵法运行时间明显缩短,与分割效果稍差的二维对称Tsallis交叉熵法相比,运行时间平均节省30%左右。
| 分割方法 | 储粮害虫图像1 | 储粮害虫图像2 | 黑斑纸病图像 | 孔洞纸病图像 | ||||
| 阈值 | 时间/s | 阈值 | 时间/s | 阈值 | 时间/s | 阈值 | 时间/s | |
| 二维最大 Shannon熵法[9] |
(91,98) | 0.345 | -108,109 | 0.535 | (34,36) | 0.338 | -143,134 | 0.237 |
| 二维Shannon 交叉熵法[12] |
(75,90) | 0.415 | -132,133 | 0.625 | (37,37) | 0.389 | -123,126 | 0.404 |
| 二维Tsallis 熵法[13] |
(91,95) | 0.429 | (71,73) | 0.506 | (32,32) | 0.452 | -118,119 | 0.382 |
| 二维对称 Tsallis交叉熵法[14] |
(37,39) | 0.479 | (41,44) | 0.634 | (6,8) | 0.469 | -162,171 | 0.43 |
| 本文方法 | (8,17) | 0.311 | (75,90) | 0.485 | (1,7) | 0.291 | -161,158 | 0.291 |
文中提出了二维非对称Tsallis交叉熵阈值分割方法。以储粮害虫和纸病2类图像为例的大量实验结果表明,通过参数q的合理设置,该方法的图像分割效果比起二维最大Shannon熵法、二维Shannon交叉熵法、二维Tsallis熵法具有明显的优势,总体上也比二维对称Tsallis交叉熵法的分割效果更理想,区域间对比度更高。同时引入了人工蜂群优化算法,该方法与粒子群优化算法相比,能够避免陷入局部极值,提高了搜索全局阈值的遍历性,并且具有较快的收敛速度。所提出的基于人工蜂群优化的二维非对称Tsallis交叉熵阈值分割方法在运行速度上,也比二维对称Tsallis交叉熵法提高了30%左右,运行时间明显减少。
| [1] | 吴一全, 朱兆达. 图像处理中阈值选取方法30年(1962—1992)的进展(一)[J]. 数据采集与处理, 1993, 8(3): 193-201. WU Yiquan, ZHU Zhaoda. 30 years (1962-1992) of the developments in threshold selection methods in image processing (1)[J]. Journal of Data Acquisition & Processing, 1993, 8(3): 193-201. |
| [2] | 吴一全, 朱兆达. 图像处理中阈值选取方法30年(1962—1992)的进展(二)[J]. 数据采集与处理, 1993, 8(4): 268-282. WU Yiquan, ZHU Zhaoda. 30 years(1962-1992) of the developments in threshold selection methods in image processing (2)[J]. Journal of Data Acquisition & Processing, 1993, 8(4): 268-282. |
| [3] | SEZGIN M, SANKUR B. Survey over image thresholding techniques and quantitative performance evaluation[J]. Journal of Electronic Imaging, 2004, 13(1): 146-165. |
| [4] | KAPUR J N, SAHOO P K, WONG A K C. A new method for the grey-level picture thresholding using the entropy of the histogram[J]. Computer Vision, Graphics and Image Processing, 1985, 29(1): 273-285. |
| [5] | ABUTALEB A S. Automatic thresholding of gray-level picture using two-dimensional entropies[J]. Pattern Recognition,1989, 47(1): 22-32. |
| [6] | CHEN W T, WEN C H, YANG C W, et al. A fast two-dimensional entropic thresholding algorithm [J]. Pattern Recognition, 1994, 27 (7): 885-893. |
| [7] | 龚坚, 李立源, 陈维南. 二维熵阈值分割的快速算法[J].东南大学学报, 1996, 26 (4): 31-36.GONG Jian, LI Liyuan, CHEN Weinan. A fast tow-dimensional entropic thresholding method [J]. Journal of Southeast University, 1996, 26(4): 31-36. |
| [8] | DU F, SHI W K, CHEN L Z, et al. Infrared image segmentation with 2D maximum entropy method based on particle swarm optimization[J]. Pattern Recognition Letters, 2005, 26(5): 597-603. |
| [9] | LI C K, LEE C H. Minimum cross entropy thresholding[J]. Pattern Recognition, 1993, 26(4): 617- 625. |
| [10] | 雷博, 范久伦. 灰度图像的二维交叉熵阈值分割法[J]. 光子学报, 2009, 38(6): 1572-1576.LEI Bo, FAN Jiulun. Two-dimensional cross-entropy thresholding segmentation method for gray-level images [J]. Acta Photonica Sinica, 2009, 38(6): 1572- 1576. |
| [11] | 吴一全, 张晓杰, 吴诗婳. 基于混沌弹性粒子群优化与基于分解的二维交叉熵阈值分割[J]. 上海交通大学学报, 2011, 45(3): 301-307. WU Yiquan, ZHANG Xiaojie, WU Shihua. Two-dimensional cross entropy thresholding based on chaotic resilient particle swarm optimization or decomposition [J]. Journal of Shanghai Jiaotong University, 2011, 45(3): 301-307. |
| [12] | SAHOO P K, ARORA G. Image thresholding using two-dimensional Tsallis-Havrda-Charvát entropy [J]. Pattern Recognition Letters, 2006, 27 (6): 520-528. |
| [13] | 朱炜, 徐玉如, 秦再白. 一种新的基于二维Tsallis 熵的阈值方法[J]. 计算机工程与应用, 2007, 43(27): 54-58.ZHU Wei, XU Yuru, QIN Zaibai. New thresholding method using tow-dimensional Tsallis entropy[J]. Computer Engineering and Applications, 2007, 43(27): 54-58. |
| [14] | WU Yiquan, ZHANG Xiaojie, WU Shihua. Image thresholding using two-dimensional Tsallis cross entropy based on either chaotic particle swarm optimization or decomposition[J]. China Communications, 2011, 8(7): 111-121. |
| [15] | 张金矿, 吴一全. 基于Tent映射CPSO的二维斜分指数阈值分割[J]. 信号处理, 2010, 26(5): 703-708.ZHANG Jinkuang, WU Yiquan. Image thresholding based on 2-D oblique exponent entropy method and Tent map chaotic particle swarm algorithm[J]. Singal Processing, 2010, 26(5): 703-708. |
| [16] | FURUICHI S, YANAGI K, KURIYAMA K. Fundamental properties of Tsallis relative entropy[J]. Journal of Mathematical Physics, 2004, 45(12): 4868-4877. |
| [17] | PAULO S R, GILSON A G. Computing the q-index for tsallis nonextensive image segmentation[C]//SIBGRAPI 09: Proceedings of the 2009 XXII Brazilian Symposium on Computer Graphics and Image Processing. Rio de Janiero, 2009: 232-237. |
| [18] | 吴一全, 沈毅, 刚铁, 等. 基于二维对称Tsallis交叉熵的小目标图像阈值分割[J]. 仪器仪表学报, 2011, 32(10): 2161-2167. WU Yiquan, SHEN Yi, GANG Tie, et al. Thresholding for small target image based on 2-D symmetric Tsallis cross entropy[J]. Chinese Journal of Scientific Instrument, 2011, 32(10): 2161-2167. |



