2. 辽宁科技大学 研究生院, 辽宁 鞍山 114051
2. Graduate school, Liaoning University of Science and Technology, Anshan 114051, China
路径规划是移动机器人领域中一个重要的研究方向,而在面对各种障碍的环境中,如何成功地避开障碍物寻找一条最优路径,又是机器人路径规划中的重要研究课题。根据蚂蚁“寻找食物”的群体行为,意大利学者Dorigo M等于1991年在法国巴黎召开的第一届欧洲人工生命会议(European Conference on Artificial Lif,ECAL)上最早提出了一种新型的仿生算法——蚁群算法[1],蚁群搜索食物的过程与机器人路径规划有着惊人的相似,都是寻找一条从起始点到终点避障的最优路径。蚁群算法固然具有分布式并行计算机制、易于与其他方法结合、具有较强的鲁棒性等优点,但搜索时间长、易陷于局部最优、面对凹形障碍物容易陷入死锁是其最为突出的缺点[2]。
文中首先简单介绍蚁群算法数学模型,然后引入改进蚁群算法,针对一般蚁群算法在构造解的过程中,蚁群收敛速度慢且容易陷入局部最优,通过建立α(信息素启发式因子)β(期望启发式因子)的互锁关系,动态自适应调整α、β;其次针对蚁群算法在面对凹形障碍物易陷入死锁,降低搜索效率,提出了广义信息素更新规则。接着将改进算法与传统蚁群算法进行仿真对比(以TSP作为仿真算例),通过仿真结果证明了改进算法在提高收敛速度,避免蚁群算法陷入局部最优方面的可行性和优越性。并将改进蚁群算法运用到机器人避障,通过仿真实验,取得了较好实验效果,进一步验证了该改进算法的有效性和实用性(利用栅格法进行环境建模)。最后,进行了进一步总结与分析。
1 蚁群算法基本原理及数学模型蚁群算法是科学家受自然界中真实蚁群觅食行为的启发,经过长期研究发现:单个蚂蚁虽没有视觉,也无法掌握附近地理信息,但运动时会通过在路径上释放出一种特殊的分泌物——信息素来寻找路径[3]。当运动路径上突然出现障碍物时,蚂蚁会通过信息素相互传递信息而最终找到一条躲避障碍物的最优路径[4]。蚁群算法具有分布式并行计算机制,易于与其他方法结合且实现简单的优点。这也正是其最早成功应用解决著名TSP问题的原因[5]。
蚂蚁k(k=1,2,···,m)在运动过程中,根据各条路径上的信息量决定其转移方向。用禁忌tabuk(k=1,2,···,m)来记录蚂蚁k当前所走过的节点,蚂蚁根据各条路径上的信息量及路径的启发信息来计算状态转移概率。Pkij(t)表示t时刻蚂蚁k由节点i转移到节点j的状态转移概率[6]:
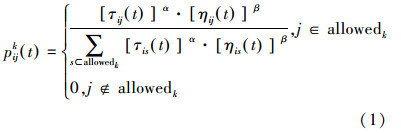

dij表示相邻节点之间的距离。对蚂蚁k而言,dij越小,则ηij(t)越大,Pijk(t)也就越大。显然,该启发函数表示蚂蚁从节点i转移到节点j的期望程度。对蚂蚁k而言,在每只蚂蚁走完一步或者完成对所有n个节点的遍历后,要对残留信息进行更新处理。这种更新策略模仿了人类大脑记忆的特点,在新信息不断存入大脑的同时,存储在大脑中的旧信息随着时间的推移逐渐淡化,甚至忘记。由此,t+n时刻在路径(i,j)上的信息量按式(3)和(4)进行调整[8]:
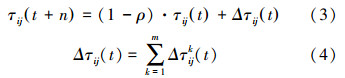
ρ表示信息素挥发系数,则1-ρ表示信息素残留因子,为了防止信息素无限积累,ρ的取值范围为ρ∈[0,1);Δτij(t)表示本次循环中路径(i,j)上的信息素增量,初始时刻Δτij(t)=0,Δτijk(t)表示第k只蚂蚁在本次循环中留在路径(i,j)上的信息量[9]。
其中Δτkij(t)按式(5)进行:

Lk 为第k只蚂蚁在本次循环中所走过的路径长度,Q为信息素强度。
2 改进蚁群算法与传统蚁群算法相比,文中提出的改进算法的特点是:1)改进算法用动态自适应调整α、β的值,代替传统蚁群算法中固定值α、β,从而提高算法收敛速度,并逃离局部最优;2)为了避免蚁群在面对凹形障碍物时容易陷入其中并进入死锁状态,改进算法采用广义信息素更新规则,代替传统蚁群算法中的信息素更新规则。
2.1 问题描述蚁群算法在实现过程中,利用禁忌表对已访问的节点进行存储,即下一步选择的节点只能为未访问节点。这样就会导致有些蚂蚁在面对凹形障碍物时,极易陷入其中并出现后续无节点可选的情况,进而进入“死锁”状态。凹形障碍物如图 1所示。路径1→4→3,1→4→2,2→4→3,2→4→1,3→4→1,3→4→2是陷入凹形障碍物而未进入“死锁”的路径;而路径1→4→5,2→4→5,3→4→5是陷入凹形障碍物并进入“死锁”的路径。显然,若蚂蚁陷入凹形障碍物并进入“死锁”路径,将会使最终的有效蚂蚁的数量小于初始蚂蚁数量,这不但会影响最优解的探寻,降低算法收敛速度,还会减缓局部最优的逃离;若蚂蚁陷入凹形障碍物并未进入“死锁”路径,蚂蚁虽然并未停止搜索,但路径1→4→3,1→4→2的距离显然长于路径1→2→3,1→2,也即该路径上的蚂蚁做了无用功,从而导致整个蚁群能量损耗,在一定程度上降低了蚁群搜索速度,延长了搜索时间。
 |
| 图 1 凹形障碍物Fig. 1 The concave obstacle |
对于凹形障碍物,一种常见的处理方法是在环境建模时,将实际环境的凹形障碍物进行凸化处理,即将障碍物进行填补,这种方法虽然可以消除凹形障碍物,但以牺牲对环境的适应性来换取算法的运行速度,且在实际环境中缺乏可行性[10]。
鉴于以上问题,通过引入文中改进蚁群算法提高蚁群收敛速度,扩大蚁群搜索空间,有效避开凹形障碍物是非常有必要和有意义的。
2.2 改进算法描述定义1 α、β的动态自适应调整。是指通过建立α(信息素启发式因子)与β(期望启发式因子)的互锁关系,即对不同的迭代次数NC,α、β会对应取不同的值,进而在整个过程中扩大蚁群搜索空间,使搜索路径逃离局部最优。
根据蚁群算法搜索情况自适应动态调整信息启发因子α和期望启发式因子β,采用迭代次数NC的阶梯函数α(NC),β(NC)代替常数项α、β,按式(6)和(7)进行调整:
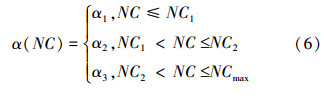

在搜索过程中为了达到平衡,式(6)、(7)中信息启发因子α和期望启发式因子β是互锁的关系,即αi+βi=M(其中M为一定值)。由于α、β值过大或过小都易使蚁群的搜索过早陷入局部最优[11]。结合其他改进算法中α、β的取值经验与分析,同时通过仿真实验分析,确定当1≤α≤9,1≤β≤9更有利于整个改进算法动态调整。开始时信息素浓度差别不大,以各个节点之间的距离为主要调整因素,这样有利于提高路径搜索速度,即信息启发因子α(1≤α1<5)先取值较小,相对应的期望启发式因子β(5<β1≤9)取值较大[12];随着迭代次数增加,各条路径的信息素也得到了积累,此时选择信息素浓度为主要调整因素进行全局搜索,即信息启发因子α(5<α2≤9)先取较大值,相对应的期望启发式因子β(1≤β2<5)取值较小;随着迭代次数的继续增加,为了防止由于信息素积累的正反馈机制作用而陷入局部最优,进而改为各个节点距离为主要调整因素,即信息启发因子α(1<α3≤5)先取值较小,相对应的期望启发式因子β(5≤β3<9)取值较大。
定义2 广义信息素更新规则。是指每只蚂蚁在路径的搜索过程中,碰到凹形障碍物采用新的信息素更新规则。当遇到凹形障碍物并陷入“死锁”则对该路径上的信息素更新采用“清零”方式;当遇到凹形障碍物并未陷入“死锁”时,为了保证整个蚁群的搜索空间,对该路径上的信息素更新采用“渐灭”方式。
设第i(i=1,2,···,k)只蚂蚁在t时刻所对应的ji(i=1,2,···,k)这条路径为陷入凹形障碍物的路径,则该路径上的信息素按式(8)~(10)进行更新[13]:

算法收敛性分析 设k只蚂蚁中,第i只蚂蚁陷入凹形障碍物并进入死锁,由式(8)~(10)可见,由于X=1,此时路径ji上遗留信息素xji将会被“清零”;同理对于陷入凹形障碍物未进入死锁的蚂蚁,由式(8)~(10)可见,随着N的不断增加且1-ρ∈[0,1),xji将以指数的方式递减,也即路径ji上遗留信息素xji将会被“渐灭”最终趋于零。
2.3 改进算法实现步骤1) 初始化
初始化改进蚁群算法的最大迭代次数NCmax,蚁群的蚂蚁数m,以及ρ,Q等参数进行初始化[14]。
2) 根据转移概率公式选择下一个节点
蚂蚁按照转移概率公式(1)进行选择,其中α、β的值按式(6)、(7)进行动态自适应调整,每次转移之后对已走过的路径进行记录,并将已访问节点加入禁忌表。
3) 记录每一代每一只蚂蚁的觅食路径和路径长度将蚁群中迭代一次的蚂蚁路径及路径长度进行记录,并写入细胞存储结构CELL。
4) 更新信息素
对各条路径的节点进行判断,若已访问的节点中包含凹形障碍物节点,则该节点对应的路径信息素按式(8)~(10)进行更新;否则按式(3)~(5)进行信息素更新。
5) 判断终止条件
当算法迭代次数大于设定最大迭代次数NCmax或算法给出的最优解满足目标条件时,则退出程序,输出最优解。
3 仿真实验及其分析 3.1 TSP仿真算例验证为了验证文中所提改进算法的可行性和有效性,针对传统蚁群算法搜索时间长、易陷于局部最优缺点,以传统蚁群算法为对比,基于TSP仿真算例进行实验分析。实验中重要参数设置如表 1所示。
| 算法 | 参数 | |||||
| m | α | β | ρ | Q | NC max | |
| 传统蚁群算法 | 32 | 1 | 5 | 0.5 | 0.5 | 300 |
| 改进蚁群算法 | 32 | 按式(6)及(7)进行调整 | 0.5 | 0.5 | 300 | |
仿真实验1 将改进算法与传统蚁群算法基于不同规模的TSP进行仿真对比,具体实验结果如图 2~4所示。
图 2为遍历32个目标所得仿真图,图 3为遍历56个目标所得仿真图。图 2、3中实线代表改进蚁群算法,点划线代表传统蚁群算法 (图 2、3的上半部分是所提的改进蚁群算法与传统蚁群算法平均距离仿真对比;下半部分是最短路径距离仿真对比)。图 4为采用改进蚁群算法遍历56个目标所搜索到的最优路径(1为起始目标点,56为终止目标点)。
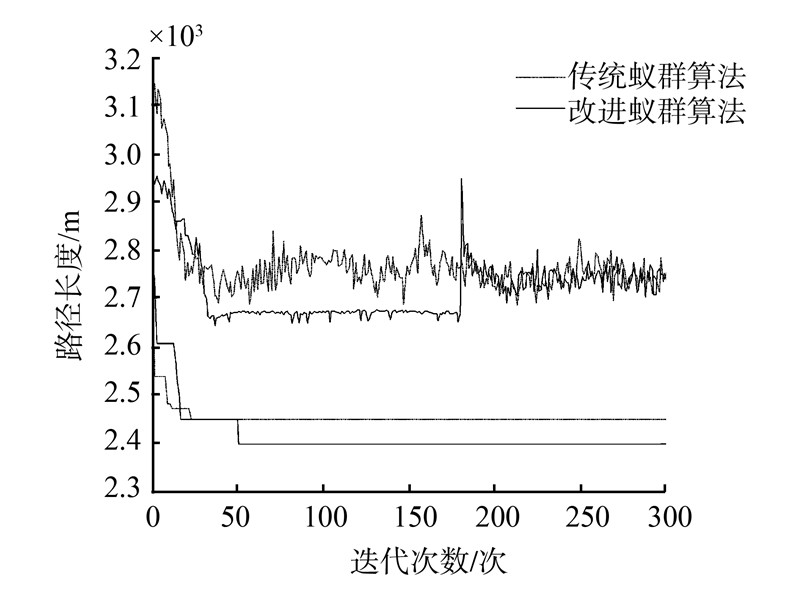 |
| 图 2 基于32个目标的平均距离与最短距离Fig. 2 Average distance and the shortest distance based on 32 goals |
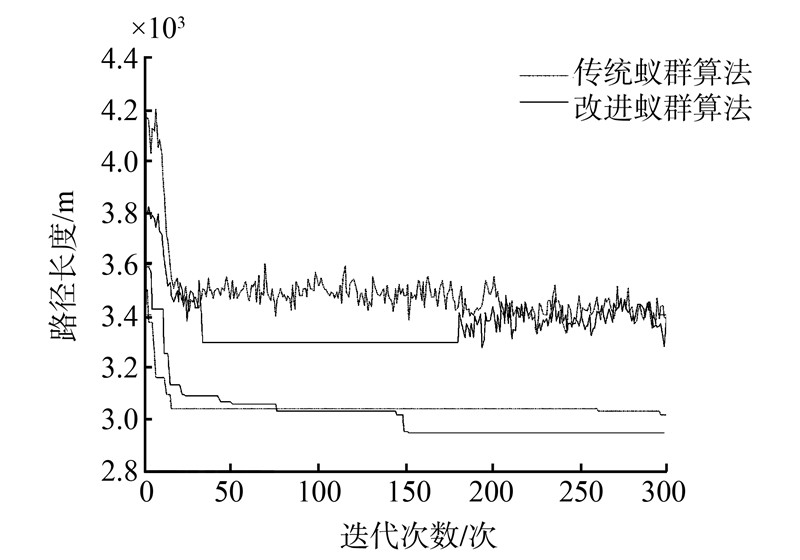 |
| 图 3 基于56个目标的平均距离与最短距离Fig. 3 Average distance and the shortest distance based on 56 goals |
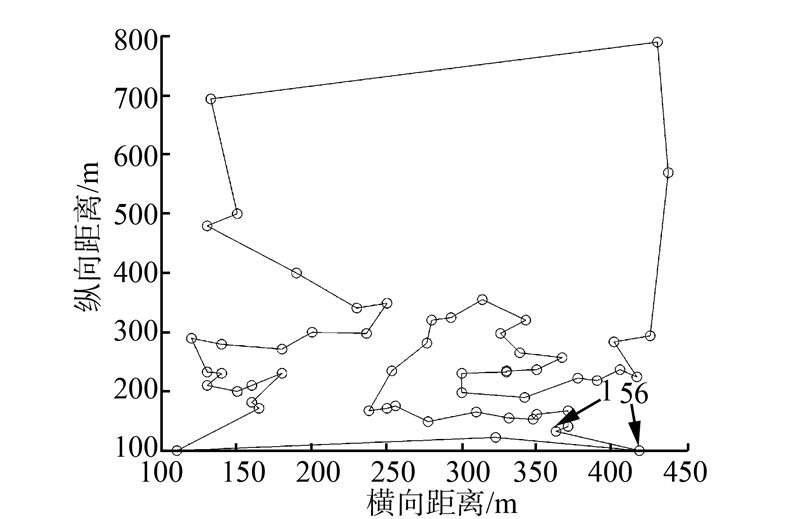 |
| 图 4 最优路径Fig. 4 The optimal path |
具体仿真数据分析如表 2所示:
| 算法 | 最短距离/ m |
平均距离/ m |
运行时间/ s |
| 传统蚁群算法(遍历 32个目标) |
2.4417e+003 | 2.8580e+003 | 32.156000 |
| 改进蚁群算法(遍历 32个目标) |
2.3966e+003 | 2.7204e+003 | 29.172000 |
| 传统蚁群算法(遍历 56个目标) |
3.0148e+003 | 3.5129e+003 | 59.316000 |
| 改进蚁群算法(遍历 56个目标) |
2.9426e+003 | 3.3599e+003 | 43.204000 |
由表 2可以看出,基于不同规模的TSP仿真算例,改进的蚁群算法所获得的最短距离与平均距离明显优于传统蚁群算法,且整个运行时间也少于传统蚁群算法。通过不同规模仿真实验对比,验证了所提出的改进算法的可行性和有效性。
3.2 改进算法在机器人避障碍中的应用为了进一步验证改进蚁群算法的可行性,将所提改进蚁群算法运用到机器人避障。为了便于蚁群算法搜索到最优路径,采用栅格法进行静态已知环境建模,同时选取了数量更多、分布更为复杂的障碍物[15]。设机器人的工作空间为二维平面上的有限区域AS,起始点B和目标点E。文中路径规划的优化准则为路径最短,即寻找一条从B到E避开障碍物的最短路径[16]。工作空间AS由200个1×1大小的方格组成,AS的规模为10行×10列。最短路径问题的目标函数可表示为式(11):
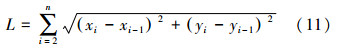
按从左到右﹑从上到下的顺序对栅格进行编号(1~100) ,同时设机器人工作空间由M行N列栅格组成,其中每个栅格是边长为1的正方形小格,将障碍物地图用一个二维数组矩阵map(M,N)表示为[18]:
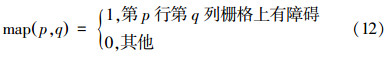
实验方法是将改进算法和传统蚁群算法分别在上述所构造的环境中进行移动机器人路径规划(其中每一栅格都为1×1正方形,且大小相等,起始栅格和目标栅格是预先指定的)。文中所做的仿真实验是在MATLAB数值分析工具下进行的。
仿真实验2 实验环境为10×10栅格环境,设定出发点的栅格序号为1,目标点的栅格序号为100(栅格对应的序号是从左上角开始,从左到右,从上到下依次为1~100),具体实验结果如图 5~9所示。
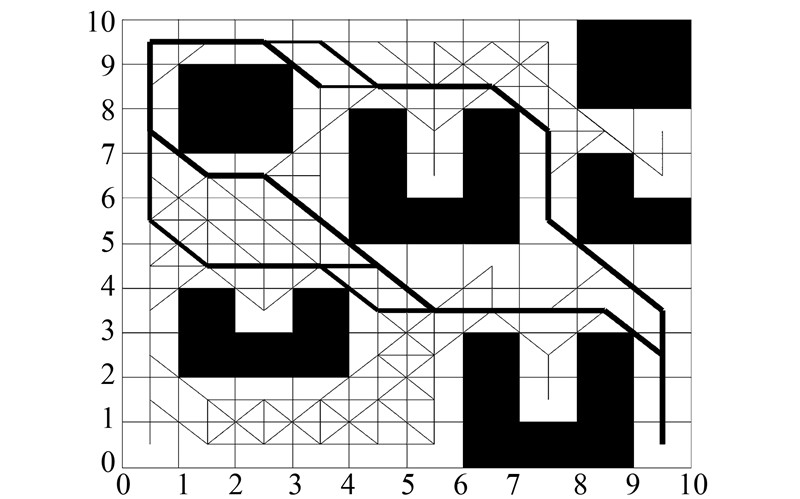 |
| 图 5 基于改进蚁群算法的机器人各代避障路线Fig. 5 The obstacle avoidance path of various generation robot based on the improved algorithm |
图 5、6为改进蚁群算法经过150次迭代后所得到的机器人各代避障路线及对应的最终收敛曲线;图 7、8为传统蚁群算法经过150次迭代后所得到的机器人各代避障路线及对应的最终收敛曲线;图 9为基于改进蚁群算法得到的机器人避障碍最优路线;通过上述仿真结果可以得出如下结论:
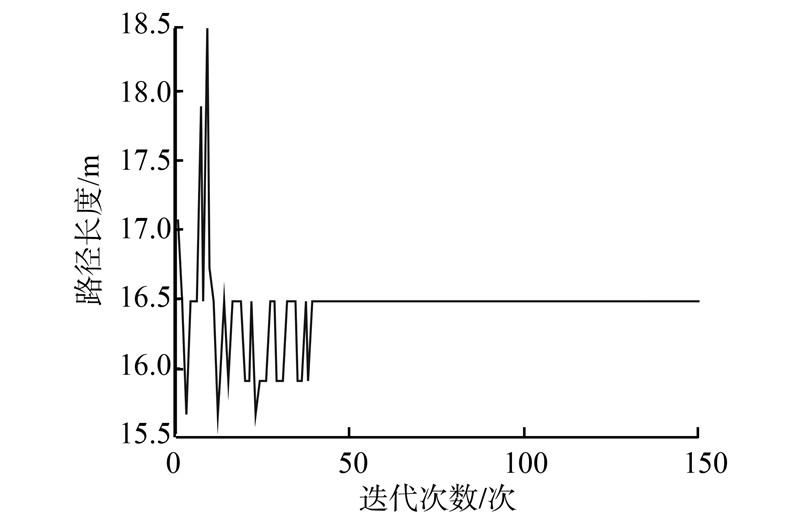 |
| 图 6 收敛曲线(基于改进蚁群算法)Fig. 6 Convergence curve (based on the improved algorithm) |
 |
| 图 7 基于传统群算法的机器人各代避障路线Fig. 7 The obstacle avoidance path of various generation robot based on the general algorithm |
 |
| 图 8 传统蚁群算法收敛曲线Fig. 8 Convergence curve based on the general algorithm |
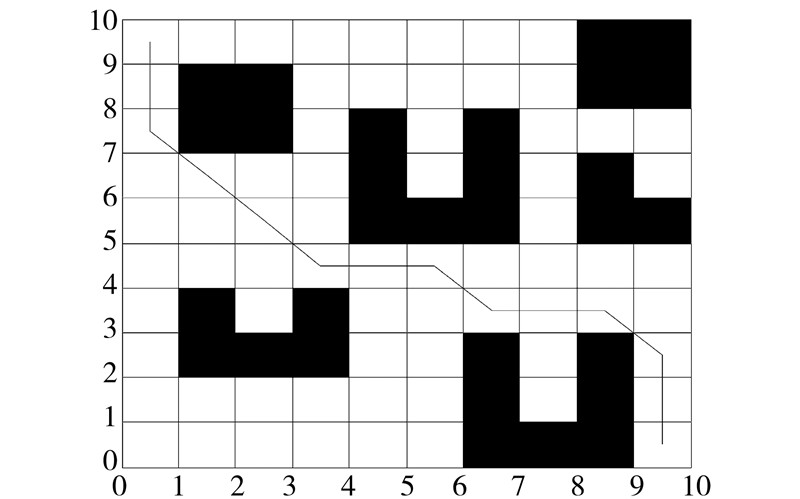 |
| 图 9 机器人避障最优路线Fig. 9 Robot obstacle avoidance optimal route |
1) 由图 5、7对比分析,可以得出基于改进蚁群算法的各代机器人在面对凹形障碍物时有更多的选择避开凹形障碍物的安全路径,保障了整个群体的性能;而基于传统蚁群算法的各代机器人,在面对凹形障碍物时更易陷入其中并进入“死锁”,减少了群体中有效个体的数量,从而影响整个群体性能。
2) 由图 6、8对比分析可知,基于改进蚁群算法的机器人在凹形障碍物的环境中经过40多次迭代就收敛到最优路径;而基于传统蚁群算法的机器人则要经过80多次迭代才能收敛到最优路径,显然改进蚁群算法的收敛速度明显优于传统蚁群算法。
3) 图 9的仿真结果进一步验证了改进算法的可行性及在凹形障碍物中寻优的高效性。
4 结束语在原有蚁群算法的基础上,首先针对蚁群算法在构造解的过程中收敛速度慢且容易陷入局部最优,提出了动态自适应调整α、β策略;其次针对蚁群算法在面对凹形障碍物易陷入死锁,提出了广义信息素更新规则。通过仿真实验将改进蚁群算法与一般蚁群算法进行对比分析,仿真结果显示,该改进算法在一定程度上提高了搜索速度,有效地弥补了传统蚁群算法容易陷入局部最优的劣势[19]。最后将改进蚁群算法应用到机器人避障,并取得了较好实验效果,仿真结果进一步验证了改进算法的可行性及在凹形障碍物中成功摆脱陷阱寻找最优路径的高效性。不足之处:该仿真的障碍物环境为静态已知环境,如果为动态未知环境,则机器人不一定能成功摆脱凹形障碍物[20]。这也是以后需要进一步改进和研究的地方。如果将该改进算法应用到其他领域,如无人驾驶车辆中进行起点和终点已知情况下的最短路径无碰撞行驶,也是具有指导意义的。
| [1] | COLORNI A, DORIGO M, MANIEZZO V. Distributed optimization by ant colonies[C]//Processings of the 1st European Conference on Artificial Life.Paris, France, 1991: 134-142. |
| [2] | 徐利超, 张世武. 基于改进蚁群算法的障碍环境下路径规划研究[J].机械与电子, 2013 (7): 61-64.XU Lichao, ZHANG Shiwu. Study of path planning in obstacle environment based on an improved ant algorithm[J]. Machinery & Electronics, 2013,(7): 61-64. |
| [3] | 朱绍伟,徐夫田,腾兆明.一种改进蚁群算法求解最短路径的应用[J].计算机技术与发展, 2011(7): 202-205.ZHU Shaowei, XU Futian, TENG Zhaoming. Application of improvement ants algorithm in solving shortest path[J]. Computer Technology and Development,2011, 21(7): 202-205. |
| [4] | 柳长安, 鄢小虎, 刘春阳,等. 基于改进蚁群算法的移动机器人动态路径规划方法[J]. 电子学报, 2011, 39(5):1220-1224. LIU Changan, YAN Xiaohu, LIU Chunyang, et al. Dynamic path planning for mobile robot based on improoved ant colony optimization algorithm[J]. Acta Electronica Sinica, 2011, 39(5): 1220-1224. |
| [5] | 段海滨. 蚁群算法原理及其应用[M]. 北京: 科学出版社, 2005: 176-181. |
| [6] | GUTJAHR W J. A graph-based ant system and its convergence [J]. Future Generation Computer Systems, 2000, 16(8): 873-888. |
| [7] | 周明秀, 程科, 王正霞.动态路径规划中的改进蚁群算法[J]. 计算机科学, 2012, 40(1): 314-316. ZHOU Mingxiu, CHENG Ke, WANG Zhengxia. Improved ant colony algorithm with planning of dynamic path[J]. Computer Science, 2012, 40(1): 314-316. |
| [8] | 王越, 叶秋冬. 蚁群算法在求解最短路径问题上的改进策略[J]. 计算机工程与应用, 2012, 48(13): 35-38.WANG Yue, YE Qiudong. Improved strategies of ant colony algorithm for solving shortest path problem[J].Computer Engineering and Applications, 2012, 48(13):35-38. |
| [9] | 赵凯, 李声晋, 孙娟, 等.改进蚁群算法在移动机器人路径规划中的研究[J]. 微型机与应用, 2013, 32(4): 67-70.ZHAO Kai, LI Shengjin, SUN Juan, et al. Research of improved ant colony algorithm in mobile robot path planning[J]. Microcomputer & its Applications, 2013, 32(4): 67-70. |
| [10] | 温如春, 汤青波, 杨国亮. 基于改进蚁群算法的移动机器人路径规划[J]. 兵工自动化, 2010, 29(8): 69-70. WEN Ruchun, TANG Qingbo, YANG Guoliang. Mobile robot's path planning based on improved ant colony algorithm[J]. Ordance Industry Automation, 2010, 29(8): 69-70. |
| [11] | 张颖, 陈雪波. 广义蚁群算法及其在机器人队形变换中的应用[J]. 模式识别与人工智能, 2007, 19, 20(3): 3-8.ZHANG Ying, CHEN Xuebo. General ant colony algorithm and its applications in robot formation[J]. Pattern Recognition and Aitificial Intelligence, 2007, 19, 20(3): 3-8. |
| [12] | JACKSON D E, HOLCOMBE M, RATNIEKS F L W. Trail geometry gives polarity to ant foraging networks [J].Nature, 2004, 432(7019):907-909. |
| [13] | 贾振华, 斯庆巴拉, 王慧娟. 基于启发式机器人路径规划仿真研究[J]. 计算机仿真, 2012, 29(1): 135-138.JIA Zhenhua, SIQING Bala, WANG Huijuan. Path planning based on heuristic algorithm[J]. Computer Simulation, 2012, 29(1): 135-138. |
| [14] | AI-TAHARWA I, SHETA A, AI-WESHAN M. A mobile robot path planning using genetic algorithm in static environment [J]. Journal of Computer Sciences, 2008, 4(4): 341-344. |
| [15] | YAO L M, DUAN H B, SHAO S. Adaptive template matching based on improved ant colony optimization[C]//Proceedings of International Workshop on Intelligence Systems and Applications. [s.l.], 2009:1-4. |
| [16] | BROOKS R A. Solving the find-path problem by good representation of free space [J]. IEEE Trans on System Man and Cybernetics, 1983, 13(3): 190-197. |
| [17] | JANET J A. The essential visibility graph: an approach to global motion planning for autonomous mobile robots[C]//IEEE International Conference on Robotics and Automation. [s.l.], 1995: 1958-1963. |
| [18] | EMILIO F. Real-time motion planning for agile autonomous vehicles [J]. Journal of Guidance, Control and Dynamics, 2002, 25(1):116-129. |
| [19] | BONABEAU E, DORIGO M, Theraulaz G. Inspiration for optimization from social insect behavior [J]. Nature, 2000, 406(6): 39-42. |
| [20] | DORIGO M, DI CARO G, GAMBARDELLA L M. Ant algorithms for discrete optimization [J]. Artificial Life, 1999, 5(2): 137-172. |



