2. 福建农林大学 计算机与信息学院, 福建 福州 350002;
3. 山东财经大学 计算机科学与技术学院, 山东 济南 250014
2. College of Computer and Information Science, Fujian Agriculture and Forestry University, Fuzhou 350001, China;
3. School of Computer Science and Technology, Shandong University of Finance and Economics, Jinan 250014, China
图像分割就是指把图像分成各具特性的区域并提取感兴趣目标的过程,是图像处理到图像分析的关键步骤[1],也是计算机视觉的一个基本问题[2]。图像分割多年来一直得到人们的高度重视,至今已提出了各种各样的分割算法,如基于阈值的分割方法[3, 4, 5, 6, 7]、基于边缘检测的分割方法[8, 9]、基于区域的分割方法[10, 11, 12]、基于图论的分割方法[13, 14]、基于能量泛函的分割方法[15, 16]以及基于机器学习的分割方法[17, 18, 19, 20]等。
基于阈值的分割方法是各类分割算法中简单且广泛采用的方法,其基本思想是用一个或者多个阈值将待分割的图像的灰度级分为多个部分,灰度值在同一类中的像素属于同一个目标[2]。因此,阈值的选取非常关键,并决定分割的结果。常见的计算阈值的方法主要有最大类间方差法(Otsu算法)[3]、最大熵法[4, 5]以及最小误差法[7]等。上述计算阈值方法基本是在满足一定准则下通过解析式求得阈值,例如Otsu算法以目标和背景的类间方差最大或类内方差最小为准则选取阈值。然而,通过解析式求解阈值的计算量和计算复杂度会随着阈值的增加而呈指数增长。因此,一些学者将基于准则函数的阈值求解问题视为以准则函数为目标函数的优化问题,于是出现了一些基于遗传算法[21]、粒子群优化算法[22]以及差分算法[23]等的多阈值方法。得益于经典进化算法能有效求解多阈值问题,一些新颖的仿生算法用于该类问题,并呈现出较好的分割效果[24, 25, 26, 27]。
回溯搜索优化算法(backtracking search optimization algorithm,BSA)是一种新兴的仿生算法,其具有简单的结构,并能有效且快速求解各类函数优化问题[28]。然而,关于BSA算法的应用研究报道较少,特别是在图像处理及应用领域。因此,借鉴于仿生算法求解多阈值问题的有效性,本文将BSA算法应用于图像分割,提出基于BSA算法的多阈值图像分割。提出的方法将Otsu算法和最大熵法的准则函数视为目标函数,并采用BSA算法分别获取多阈值,实现图像分割。实验说明提出的方法具有更好的性能。
1 阈值法 1.1 最大类间方差法(Otsu法)最大类间方差法给予判别分析最小二乘法的原理,其根据图像的灰度特性,将图像分为不同类别,各类之间方差要求最大。假设存在m级灰度的图像P,阈值q将图像的灰度值范围[0,1,…,m-1]分为背景与目标2部分。又设pi表示灰度值为i出现的概率,则目标部分和背景的概率分别表示为
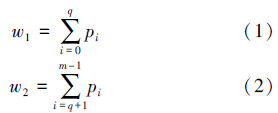
设λ、λ1、λ2分别表示图像、目标和背景的灰度值均值,则可表示为


类间方差可表示为

假设图像P存在a个阈值(q1,q2,…,qa),式(5)容易扩展多阈值类间方差,可表示为
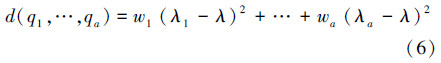
根据类间最大化准则,可通过计算式(7)获得最佳阈值:
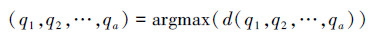
20世纪80年代以来,Shannon信息熵的概念被应用于图像阈值化处理中,其思想是利用图像的灰度分布密度函数定义图像的信息熵,并根据优化准则求得阈值。文献[4]通过使后验的上限最大化准则确定阈值,而文献[5]假定目标和背景服从2个不同的概率分布,使得信息熵最大化求得最佳阈值。
假设存在m级灰度的图像P,阈值q将图像的灰度值范围[0,1,…,m-1]分为背景与目标2部分。又设pi表示灰度值为i出现的概率,则目标和背景表示为式(1)和式(2),而它们的信息熵则可表示为
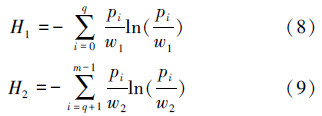
Kapur方法[5]是在图像P的总信息熵最大时,获得最佳阈值,即
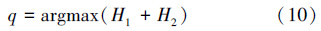
同样,式(10)很容易扩展为多阈值最大熵,可表示为
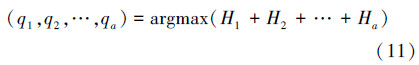
BSA算法是一种新兴的随机优化搜索技术,其结构简单,并且能够有效求解各类优化问题。另外,BSA算法也是基于种群的搜索技术,并且使用一个外部文档维护其历史种群信息以引导种群进化。
当BSA算法用于求解优化问题时,首先在解搜索空间[xj,min,xj,max] (j=1,2,…,D)内,通过均匀采样初始化候选解X和历史种群Xold:

与其他进化算法类似,BSA算法使用3个基本的遗传操作:变异、交叉和选择。
BSA算法采用随机变异策略为每个个体生成中间候选个体Vm。该策略能够有效利用历史种群的信息引导算法进化,具体公式为
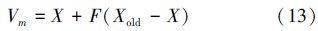
算法1 交叉策略
输入 变异个体Vm、种群X、种群规模NP、问题维数D、以及混合率mixrate。
输出 候选解T
1)初始化矩阵map(1:NP,1:D)=1;
2)均匀产生2个[0,1]之间的随机数a和b;
3)if a>b,转入4),否则转入5);
4)进行如下操作后转入第6步:
for i=1 to NP
随机生成系列u=permuting(1:D);
均匀生成1个[0,1]的随机数c;
处理map(i,1:mixrate×c×D))=0;
end for
5)进行如下操作:
for i=1 to NP
均匀生成1个[0,D]的随机整数d;
处理map(i,d)=0;
end for
6)T=Vm;
7)进行如下操作:
for i=1 to NP
for j=1 to D
if map(i,j)=1 then T(i,j)= P(i,j);
end for
end for
另外,BSA算法采用2种选择操作。第一种选择操作用于更新历史种群的信息,其完全随机下接收当前种群信息,可概括为

应用BSA算法求解多阈值问题,其实质是将多阈值准则作为目标函数,采用BSA算法搜索最优阈值,具体步骤如算法2所示。
算法2 基于BSA算法的多阈值图像分割
输入 种群规模NP、问题维数D(阈值数目)、混合率mixrate、最大迭代次数MaxIteration。
输出 最佳阈值q
1)采用式(12)初始化种群X和历史种群Xold;
2)初始化迭代计数器iter=1;
3)if iter>MaxIteration,转入11);
4)执行第1种选择操作,即执行式(14)更新历史种群;
5)执行变异操作,即执行式(13);
6)执行交叉操作获得T,即执行算法1;
7)采用式(7)或者式(11)评价T;
8)根据X和T的适应值,采用第2种选择操作获得下一代种群X。
9)获得当前最优阈值q;
10)iter=iter+1,转入3);
11)输出最优阈值q。
4 实验与结果为了分析BSA算法的多阈值图像分割性能,本文采用文献[25]中的Camera、Lena、Pepper以及Baboon等4幅图像作为待分割图像见图1,其中,每幅图像的大小为256×256。
 |
| 图 1 测试图像Fig. 1 Test images |
另外,图像峰值信噪比(peak signal to nose ratio,PSNR)作为性能指标,其中PSNR公式[24]如下:


在实验中,各算法针对每幅图像独立运行30次。每次独立运行中,最大迭代数MaxIteration为160,种群大小NP为20。
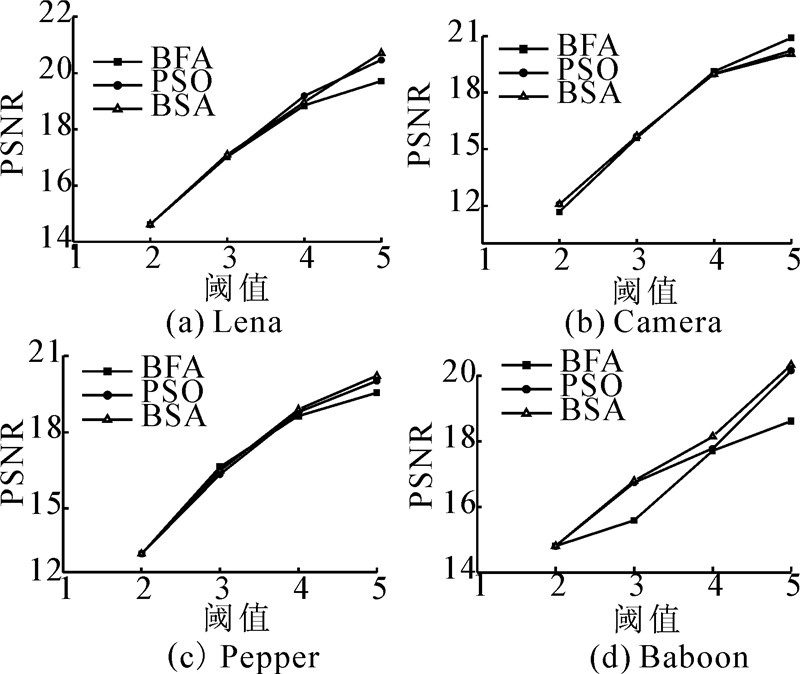
4.1 Otsu方法的实验结果表1给出了与基于传统优化算法的多阈值Otsu(MOT)[29]比较的实验结果。MOT中的适应值是将MOT中的阈值带入式(7)求得。表2列出与基于细菌算法(bacterial foraging algorithm,BFA)的Otsu多阈值[25]和带惯性权重PSO算法[30]的Otsu多阈值的实验结果。其中,PSO算法的最大和最小惯性权重分别为0.9和0.4;BFA算的参数见文献[25]。另外,图2给出各算法求解的PSNR随Otsu阈值数的变化趋势。
| 测试图像 | 阈值数目 | MOT | BSA | ||||
| 阈值 | 适应值 | PSNR | 阈值 | 适应值 | PSNR | ||
| Lena | 2 3 4 5 | 85,143 74,120,164 66.105,137,173 59,88,115,142,176 | 2 895.36 3 136.52 3 238.31 3 276.55 | 12.67 15.83 18.01 18.93 | 85,156 71,127,181 63,111,150,192 61,105,138,164,200 | 2 923.59 3 174.28 3 271.09 3 309.50 | 13.65 17.16 19.38 20.94 |
| Camera | 2 3 4 5 | 69,143 59,121,157 59,116,148,173 45,97,135,162,196 | 3 927.90 4 010.71 4 053.73 4 092.03 | 11.14 12.72 16.13 19.87 | 64,141 54,118,155 36,90,136,167 31,81,122,149,172 | 3 929.46 4 012.30 4 069.13 4 103.01 | 11.12 12.85 16.38 19.17 |
| Pepper | 2 3 4 5 | 65,132 61,116,164 57,100,136,171 44,79,110,143,173 | 3 142.25 3 364.89 3 445.22 3 498.36 | 12.505 3 15.16 16.28 17.04 | 71,147 66,129,183 46,90,135,185 42,83,121,158,193 | 3 180.47 3 396.53 3 476.78 3 533.00 | 12.87 16.57 17.69 19.47 |
| Baboon | 2 3 4 5 | 99,145 86,121,154 73,106,132,158 42,81,110,133,161 | 1 566.10 1 722.19 1 782.34 1 821.35 | 12.49 13.93 14.64 15.22 | 119,177 101,146,188 86,127,162,196 85,120,146,173,203 | 1 742.75 1 865.12 1 934.25 1 967.98 | 15.85 18.22 19.69 21.53 |
| 测试图像 | 阈值数目 | BFA | PSO | BSA | ||||||
| 阈值 | 适应值 | PSNR | 阈值 | 适应值 | PSNR | 阈值 | 适应值 | PSNR | ||
| Lena | 2 3 4 5 | 84,155 78,138,186 62,105,133,190 60,81,107,140,181 | 2923.58 3165.87 3243.88 3281.39 | 14.75 17.21 18.55 19.83 | 85,156 71,127,181 63,110,150,192 62,106,138,165,200 | 2923.59 3174.28 3271.09 3309.50 | 13.65 17.16 19.27 20.81 | 85,156 71,127,181 63,111,150,192 61,105,138,164,200 | 2923.59 3174.28 3271.09 3309.50 | 13.65 17.16 19.38 20.94 |
| Camera | 2 3 4 5 | 64,141 56,115,152 22,87,124,161 40,75,106,142,166 | 3929.46 4010.73 4056.59 4090.59 | 11.12 12.60 14.33 16.16 | 64,141 54,118,155 36,91,137,168 29,79,121,149,173 | 3929.46 4012.30 4069.16 4103.20 | 11.12 12.85 15.94 17.86 | 64,141 54,118,155 36,90,136,167 31,81,122,149,172 | 3929.46 4012.30 4069.13 4103.01 | 11.12 12.85 16.38 19.17 |
| Pepper | 2 3 4 5 | 73,147 69,127,183 40,94,125,177 50,93,144,169,193 | 3180.16 3394.44 3454.18 3506.14 | 12.79 15.25 16.55 17.78 | 71,147 66,129,183 47,91,136,185 43,84,122,159,194 | 3180.47 3396.53 3476.79 3533.05 | 12.87 16.57 17.68 19.20 | 71,147 66,129,183 46,90,135,185 42,83,121,158,193 | 3180.47 3396.53 3476.78 3533.00 | 12.87 16.57 17.69 19.47 |
| Baboon | 2 3 4 5 | 118,176 107,154,199 73,132,168,208 79,110,133,166,200 | 1742.52 1856.36 1905.70 1961.01 | 15.10 16.97 19.59 21.20 | 119,17 7101,146,188 88,127,162,197 82,118,147,172,202 | 1742.75 1865.12 1934.27 1968.39 | 15.85 18.22 19.69 21.25 | 119,177 101,146,188 86,127,162,196 85,120,146,173,203 | 1742.75 1865.12 1934.25 1967.98 | 15.85 18.22 19.69 21.53 |
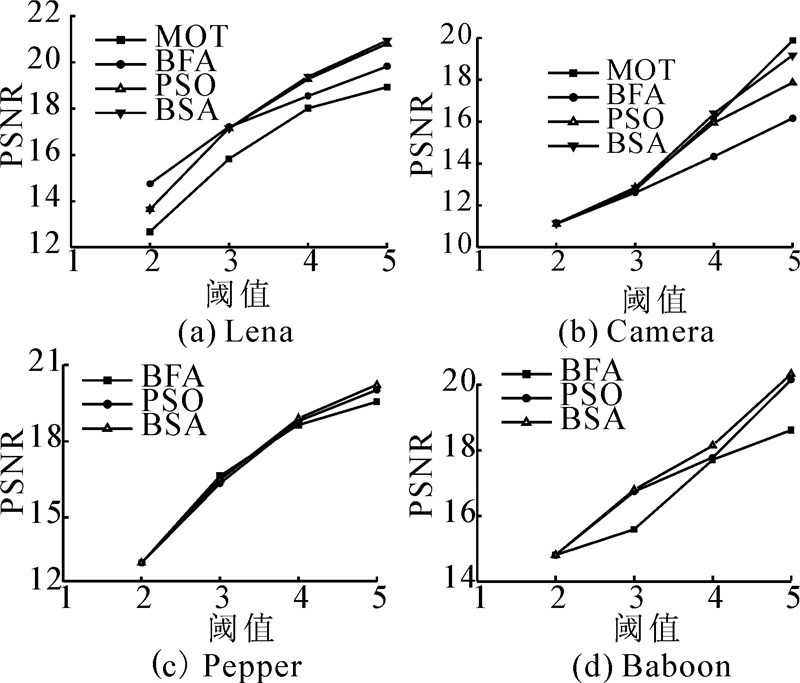 |
| 图 2 PSNR随Otsu阈值变化的趋Fig. 2 The trend of PSNR change with Otsu threshol |
从表1可知,采用BSA算法求解的阈值使得适应值都优于MOT的所得适应值;另外借助于PSNR,BSA算法也优于MOT。上述结果说明了BSA算法以Otsu的最大类间准则为目标函数求解多阈值是可行的,而且获得较好的性能。
从表2可以看出,与BFA算法比较,BSA算法求解的多阈值在目标函数适应值以及PSNR上都明显较优。另外,与PSO算法比较,在各测试图像的2和3个阈值上,BSA算法求解的多阈值与PSO算法求解的多阈值是相同的,然而在4和5个阈值上,PSO算法获得稍微较好的目标函数适应值,但是BSA算法却获得较好的PSNR。总体而言,BSA算法的多阈值与带惯性权重PSO算法的多阈值性能是相同的。图2同样说明了随阈值数的增加,BSA算法求解的PSNR趋势总体上是最好的。
4.2 Kapur方法的实验结果表3给出了不同仿生算法求解Kapur多阈值的比较结果,其中参数与4.1节相同。
| 测试图像 | 阈值数目 | BFA | PSO | BSA | ||||||
| 阈值 | 适应值 | PSNR | 阈值 | 适应值 | PSNR | 阈值 | 适应值 | PSNR | ||
| Lena | 2 3 4 5 | 92,173 66,127,191 40,91,133,179 47,83,126,186,211 | 17.72 21.95 25.63 29.22 | 14.62 17.02 18.84 19.72 | 92,173 72,127,188 52,92,140,189 48,87,128,172,207 | 17.72 21.98 25.84 29.52 | 14.62 17.03 19.19 20.46 | 92,173 72,126,188 51,92,140,189 48,87,129,172,208 | 17.72 21.98 25.84 29.52 | 14.62 17.10 18.96 20.71 |
| Camera | 2 3 4 5 | 125,192 36,99,194 57,100,143,196 19,75,118,152,201 | 17.56 21.95 26.29 30.23 | 11.66 15.60 19.13 20.91 | 124,192 37,100,192 37,92,143,196 18,56,95,143,196 | 17.56 21.97 26.54 30.50 | 12.08 15.69 18.99 20.23 | 124.192 37,100,192 37,92,143,196 18,57,94,144,196 | 17.56 21.97 26.54 30.50 | 12.08 15.69 18.99 20.05 |
| Pepper | 2 3 4 5 | 81,16 161,118,180 64,111,154,209 52,81,114,159,217 | 18.14 22.52 26.55 30.40 | 13.22 16.64 18.64 19.55 | 81,161 62,121,180 61,113,163,214 43,82,122,166,214 | 18.14 22.53 26.66 30.59 | 13.22 16.34 18.79 20.02 | 81,161 61,121,180 62,113,163,214 43,82,124,169,214 | 18.14 22.53 26.66 30.59 | 13.22 16.49 18.89 20.21 |
| Baboon | 2 3 4 5 | 93,170 83,133,194 48,91,128,191 44,79,132,164,204 | 17.22 21.42 25.35 28.99 | 14.81 15.59 17.71 18.62 | 93,170 71,127,184 48,93,138,189 48,88,128,168,205 | 17.22 21.48 25.44 29.13 | 14.81 16.75 17.78 20.16 | 93,170 71,126,184 48,93,138,190 46,88,130,169,205 | 17.22 21.48 25.44 29.13 | 14.81 16.80 18.15 20.34 |
从表3可以看出,BSA算法求解的目标函数适应值上完全优于BFA算法求解的目标函数适应值,而且借助于PSNR性能,BSA算法也优于BFA算法。另外与PSO算法比较,BSA算法求解的目标函数适应值基本上相似,但借助于PSNR,BSA算法的多阈值法总体上优于PSO算法的多阈值法。
图3给出各仿生算法求解的PSNR随Kapur阈值数的变化趋势。从图3可以看出,在多数的图像上,BSA求解的PSNR随Kapur阈值数的变化趋势优于其他2种算法。
 |
| 图 3 PSNR随Kapur阈值变化的趋势Fig. 3 The trend of PSNR change with Kapur threshold |
本文将BSA算法应用于图像分割,提出BSA算法求解的多阈值图像分割。提出方法将Otsu方法和Kapur方法的求多阈值准则函数作为目标函数,应用BSA算法求解,并实现图像分割。仿真结果说明BSA算法求解的多阈值图像分割是可行的,与其他的BFA算法和PSO算法求解的多阈值分割方法比较,本文提出的方法具有较好的性能。下一步工作将提出方法应用于更多的图像测试,包括遥感图像以及医学影像等。
| [1] | 章毓晋.图像工程[M].北京:清华大学出版社,2002:179-186. |
| [2] | 刘国英,马国锐,王雷光,等.基于Markov随机场的小波域图像建模及分割-Matlab环境[M].北京:科学出版社,2010:6-15. |
| [3] | OTSU N.A threshold selection method from gray-level histograms[J].Automatica,1975,11:23-27. |
| [4] | PUN T.A new method for grey-level picture thresholding using the entropy of the histogram[J].Signal Processing,1980,2(3):223-237. |
| [5] | KAPUR J N,SAHOO P K,WONG A K C.A new method for gray-level picture thresholding using the entropy of the histogram[J].Computer Vision,Graphics and Image Processing,1985,29(3):273-285. |
| [6] | REDDI S S,RUDIN S F,KESHAVAN H R.An optimal multiple threshold scheme for image segmentation[J].IEEE Transactions on Systems,Man,and Cybernetics,1984,14(4):661-665. |
| [7] | KITTLER J,ILLINGWORTH J.Minimum error thresholding[J].Pattern Recognition,1986,19(1):41-47. |
| [8] | CANNY J.A computational approach to edge detection[J].IEEE Transactions on Pattern Analysis and Machine Intelligence,1986,PAMI-8(6):679-698. |
| [9] | ZIOU D,TABBONE S.Edge detection techniques:an overview[J].International Journal of Pattern Recognition and Image Analysis,1998,8(4):537-559. |
| [10] | CHEN P C,PAVLIDIS T.Segmentation by texture using a co-occurrence matrix and a split-and-merge algorithm[J].Computer Graphics Image Processing,1979,10(2):172-182. |
| [11] | CHEN S Y,LIN W C,CHEN C T.Split-and-merge image segmentation based on localized feature analysis and statistical tests[J].CVGIP:Graphical Models and Image Processing,1991,53(5):457-475. |
| [12] | CHANG Y L,LI X.Adaptive image region-growing[J].IEEE Transactions on Image Processing,1994,3(6):868-872. |
| [13] | BOYKOV Y,JOLLY MP.Interactive graph cuts for optimal boundary and region segmentation of objects in N-D images[C]//Proceedings of the Eighth International Conference on Computer Vision.Piscataway,NJ:IEEE,2001:105-112. |
| [14] | GRADY L.Random walks for image segmentation[J].IEEE Transactions on Pattern Analysis and Machine Intelligence,2006,28(11):1768-1783. |
| [15] | KASS M,WITKIN A,TERZOPOULOS D.Snakes:active contour models[J].International Journal of Computer Vision,1988,1(4):321-331. |
| [16] | OSHER S,SETHIAN J A.Fronts propagating with curvature-dependent speed:algorithms based on Hamilton-Jacobi formulations[J].Journal of Computational Physics,1988,79(1):12-49. |
| [17] | ROUT S,SRIVASTAVA M J.Multimodal image segmentation using a modified Hopfield neural network[J].Pattern Recognition,1998,31(6):743-750. |
| [18] | 林开颜,徐立鸿,吴军辉.快速模糊C均值聚类彩色图像分割方法[J].中国图像图像学报,2004,9(2):159-163.LIN Kaiyan,XU Lihong,WU Junhui.A fast fuzzy C-M eans cluster ing for color image segmentation[J].Journal of Image and Graphics,2014,9(2):159-163. |
| [19] | CAO G B,WANG S L,WEI B Z,et al.A hybrid CNN-RF method for electron microscopy images segmentation[J].Journal of Biomimetics Biomaterials and Tissue Engineering,2013,18(2):1-6. |
| [20] | WANG S L,CAO G B,WEI B Z,et al.Hierarchical level features based trainable segmentation for electron microscopy images[J].Biomedical Engineering Online,2013,12(1):59-72. |
| [21] | TANG K Z,YUAN X J,SUN T K,et al.An improved scheme for minimum cross entropy threshold selection based on genetic algorithm[J].Knowledge-Based Systems,2011,24(8):1131-1138. |
| [22] | YIN P Y.Multilevel minimum cross entropy threshold selection based on particle swarm optimization[J].Applied Mathematics and Computation,2007,182(2):503-513. |
| [23] | ALI M,AHN C W,PANT M.Multi-level image thresholding by synergetic differential evolution[J].Applied Soft Computing,2014,17:1-11. |
| [24] | AGRAWAL S,PANDA R,BHUYAN S,et al.Tsallis entropy based optimal multilevel thresholding using cuckoo search algorithm[J].Swarm and Evolutionary Computation,2013,11:16-30. |
| [25] | SATHYA P D,KAYALVIZHI R.Optimal multilevel thresholding using bacterial foraging algorithm[J].Expert System with Application,2011,38(12):15549-15564. |
| [26] | HORNG M H,LIOU R J.Multilevel minimum cross entropy threshold selection based on the firefly algorithm[J].Expert System with Application,2011,38(12):14805-14811. |
| [27] | MA M,LIANG J H,GUO M,et al.SAR image segmentation based on artificial bee colony algorithm[J].Applied Soft Computing,2011,11(8):5205-5214. |
| [28] | CIVICIOGLU P.Backtracking search optimization algorithm for numerical optimization problems[J].Applied Mathematics and Computation,2013,219:8121-8144. |
| [29] | MATHWORKS.Multilevel image thresholds using Otsu′s method[EB/OL].[2014-08-22].http://www.mathworks.cn/cn/help/images/ref/multithresh.html. |
| [30] | SHI Y H,EBERHART R C.A modified particle swarm optimizer[C]//Proceedings of the 1998 IEEE World Congress on Computational Intelligence.Piscataway,NJ,1998:69-73. |



