2. 中国公路工程咨询集团有限公司, 北京 100097
2. China Highway Engineering Consulting Corporation, Beijing 100097, China
在智能交通领域,交通场景图像质量的高低直接影响对场景中车辆、行人、障碍物等目标的检测和识别。然而,图像在获取和传输的过程中往往容易被噪声污染,从而影响图像的质量。有效的去噪方法不仅能够抑制图像中的随机噪声,同时还能较好地保持重要的图像特征和细节。如果能够了解图像的某个先验统计模型,便能很大程度上地改善图像处理的效果[1]。在图像去噪领域,基于小波变换的方法已经成为了主流[2]。例如Donoho等提出阈值去噪算法[3]以及Chang等在此基础上改进得到的阈值萎缩算法[4, 5, 6]。这些去噪算法主要包括3个步骤:首先,对含噪图像进行小波变换;然后,对各细节子带上小波系数进行阈值萎缩处理;最后,通过小波逆变换重构去噪后图像。然而阈值萎缩处理主要存在2个不足:1) 如何选择一个最合适的阈值一直是个难以解决的问题;2) 在不同的尺度上,小波系数的先验统计模型并不能和信号很好地匹配[7]。研究发现,相较于目前广泛用于小波系数建模的广义高斯模型(GGM),二维广义自回归条件异方差(2D-GARCH)模型能够更准确地描述图像小波系数的统计特性,是一种更加优秀的小波系数先验模型,故本文使用2D-GARCH模型对小波系数进行建模。1D-GARCH模型[8]在金融时间序列建模中已经得到了广泛的应用,Noiboar等最早将1D-GARCH模型扩展为二维模型并用于图像的畸点探测[9],Amirmazlaghani等利用2D-GARCH模型抑制合成孔径雷达图像上的斑点噪声[10, 11]。本文利用基于果蝇优化算法的极大似然估计准确求解2D-GARCH模型的参数,获得了各细节子带的先验统计模型,在此基础上再通过最小均方误差估计对原始图像的小波系数进行估计,从而达到去噪目的。
1 2D-GARCH模型的小波系数建模 1.1 2D-GARCH模型假设yij是二维的随机变量且均值为零即E(yij)=0,若yij有如下形式则称其服从纯2D-GARCH(p1,p2,q1,q2)模型[9]:
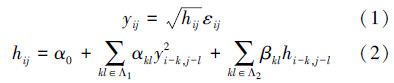
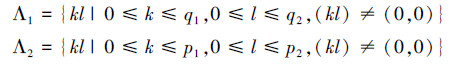
hij是yij的条件方差,εij是独立同分布的二维标准正态分布,即εij~N(0,1),(p1,p2,q1,q2)为模型的阶数。从式(2)可以看出,每一个确定的空间位置上的变量值yij的条件方差hij是由与之邻近的变量值yi-k,j-l和其条件方差hi-k,j-l决定的。现定义随机变量yij邻近位置上的变量值和条件方差的集合为
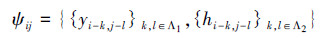
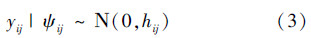
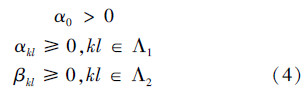
同时为了确保2D-GARCH(p1,p2,q1,q2)过程具有广义平稳性[9],需保证
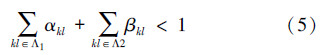
式(4)、(5)是2D-GARCH(p1,p2,q1,q2)模型有意义且具有广义平稳性的充要条件,下文的所有推导都在此约束条件下进行。
然而统计发现各子带上的小波系数的均值E(yij)≠0,那么首先对yij进行相应的去均值处理。令zij表示二维线性回归的新息:


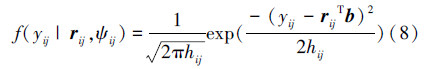

求解上述模型,即需要估计出模型中的未知参数Γ={{α0,α01,…,αq1q2,β01,…,βp1p2},b}。本文采用极大似然估计求解模型参数,现定义样本空间:
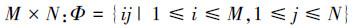
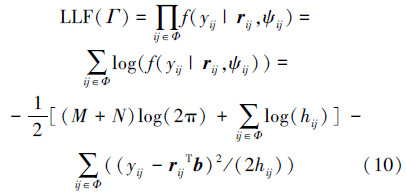
为了完成对各细节子带上小波系数的建模,必须求出使得上述对数极大似然函数取得最大值时的参数Γ。
1.2 2D-GARCH模型参数估计由于较高的模型阶数会导致计算量过大且更容易受到舍入误差的不利影响,因此本文采用2D-GARCH(1,1,1,1)模型对各细节子带建模,即未知参数为:Γ={{α0,α01,α10,α11,β01,β10,β11},b}。利用传统的线性规划方法求解式(10)的极大值问题时往往容易陷入局部最优解,对子带的准确建模产生较为不利的影响。为了尽可能地消除这种影响,本文采用果蝇优化算法[12]求解式(10)。果蝇优化算法属于进化算法的一种,对高维目标函数具有较好的寻优能力和较快收敛速度。
基于果蝇优化算法的2D-GARCH(1,1,1,1)模型参数估计的原理如下:
1) 在满足约束条件的前提下初始果蝇群体位置InitΓ_axis.其中Γ={{α0,α01,α10,α11,β01,β10,β11},b}。
2) 赋予果蝇利用嗅觉搜索食物的随机方向与距离Γi=Γ_axis+RandomValue。
3) 将Γi代入式(10)求出果蝇个体的味道浓度
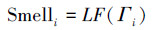
4) 找出果蝇群体中味道浓度最高的果蝇
[bestSmellbestIndex]=max(Smelli)
5) 保留最佳味道浓度与各参数的坐标,此时果蝇群体利用视觉往该方向飞去:
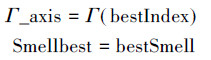
6) 进入迭代寻优,重复执行步骤2)~4),并判断味道浓度是否优于前一迭代味道浓度,若是则执行步骤5)。
为了检验模型参数估计的准确性,采用图像小波分解后第2层的水平子带上的小波系数进行参数估计实验。表1给出了该子带模型各参数的估计结果,图1是归一化的小波系数直方图和参数值为表1中各估计值的2D-GARCH(1,1,1,1)模型直方图。
| 参数 | 估计值 | 参数 | 估计值 |
| α0 | 1.3e-4 | β10 | 0.115 |
| α01 | 0.195 | β11 | 0.039 |
| α10 | 0.277 | b1 | 0.041 |
| α11 | 0.111 | b2 | 0.048 |
| β01 | 0.153 | b3 | 0.068 |
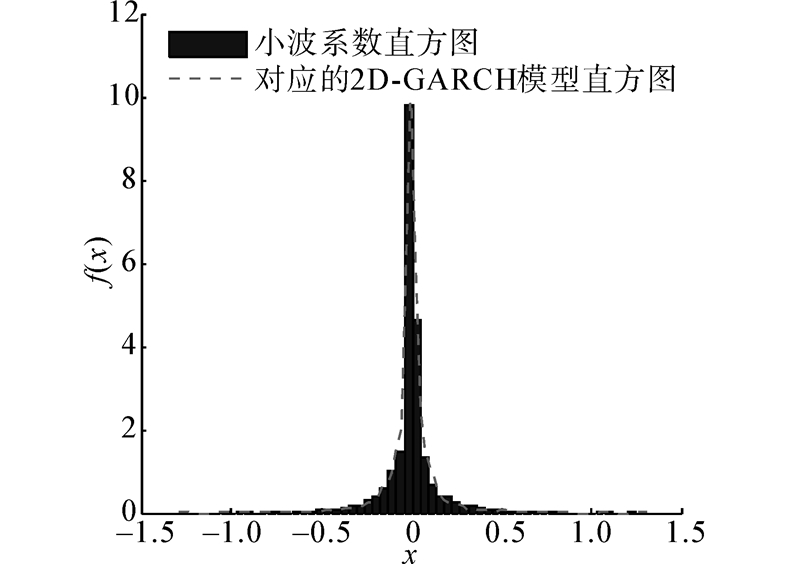 |
| 图 1 第2层水平子带的小波系数直方图Fig. 1 Histogram of the wavelet coefficients in horizontal subband at the second level of decomposition |
从图1中可以看出,小波系数的直方图和与之对应的2D-GARCH(1,1,1,1)模型直方图具有很高的拟合度,表明利用果蝇优化算法求得的模型参数估计值 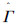 较为准确,完成了该子带上小波系数的建模。
较为准确,完成了该子带上小波系数的建模。
本文去噪算法的具体步骤如下,流程图如图2。
 |
| 图 2 本文去噪算法流程图Fig. 2 Flow chart of the proposed agorithm for image denoising |
1) 含噪图像小波分解:对被噪声污染的图像进行N层离散小波分解,得到不同尺度和方向上的子带。
2) 2D-GARCH(1,1,1,1)模型参数求解:利用果蝇优化算法求解式(10),得到各个尺度上的细节子带的模型参数。
3) 原始图像小波系数估计:在上一步估计出各尺度上的细节子带的模型参数的基础上,利用最小均方误差估计原始图像的小波系数。
4) 图像重构:通过离散小波逆变换重构去噪后的图像。令x和n分别表示原始图像和加性噪声,y=x+n表示观测到的含噪图像。首先,对含噪图像进行任意尺度的离散小波变换,从而得到了不同尺度和方向上的子带。令Xij,Nij和yij分别代表x、n和y的任意子带上的小波系数,那么有

然后对观测到的含噪图像所有细节子带上的小波系数建模,根据上一节介绍的建模方法,利用果蝇优化算法估计出每个细节子带的模型参数 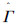 的值后得到
的值后得到
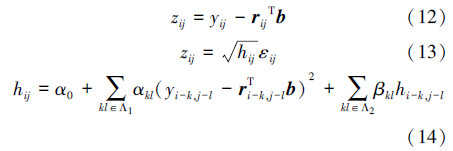
令σYij2表示Yij的条件方差即i>σYij2=hij,σN2表示噪声方差,可利用鲁棒性中值估计求得[13]
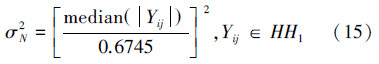
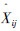 :
:
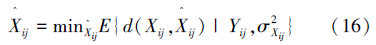

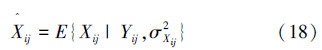
为了得到式(18)所示Xij的条件期望值,首先要计算出Xij的条件概率密度函数f(Xij|yij,σXij2),根据贝叶斯准则可得
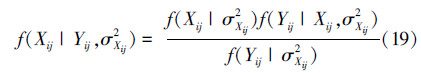
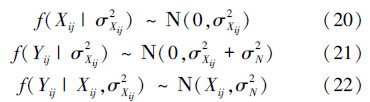
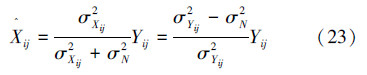
利用式(23)可以很容易地计算出原始图像各细节子带的小波系数估计值 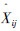 。
。
最后,通过离散小波逆变换重建去噪后的图像。
3 实验结果分析实验采用图3(a)所示含有不同强度高斯白噪声的交通场景灰度图像(Cars 256×256),并使用Daubechies(Db4)小波基[10, 11]对图像进行二层小波分解。为了检验本文算法的去噪效果,文中与维纳滤波法[14]、BayesShrink方法[15]、改进的局部窗口自适应估计(LAWML)方法[16]进行对比,并根据峰值信噪比(PSNR)来评价各算法的去噪效果。其中峰值信噪比定义为
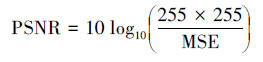
式中: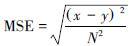 ,x和y分别代表原始未含噪声的图像和去噪后的图像,N2代表图像的尺寸。各种算法的去噪效果如表2和图3所示。
,x和y分别代表原始未含噪声的图像和去噪后的图像,N2代表图像的尺寸。各种算法的去噪效果如表2和图3所示。
| dB | |||||
| 噪声标准差 | 噪声 | Wiener | BayesShrink | LAWML | 本文方法 |
| 10 | 28.13 | 31.87 | 31.73 | 32.01 | 33.12 |
| 15 | 24.60 | 29.96 | 30.01 | 30.33 | 31.17 |
| 20 | 22.11 | 28.16 | 28.38 | 28.59 | 29.43 |
| 25 | 20.16 | 26.66 | 26.95 | 27.29 | 27.84 |
| 30 | 18.61 | 25.33 | 26.01 | 26.32 | 26.75 |
 |
| 图 3 σ=20时Cars图像4种算法的去噪比较Fig. 3 Comparison of four denoising methods for Cars image of σ=20 |
从表2中可以看出,本文方法的峰值信噪比明显高于其他方法。当噪声强度增大时,去噪效果下降的比较明显,这是因为当噪声强度过大时可能会对模型的适用范围产生一定的影响。
图3是当噪声标准差σ=20的时候各种算法的去噪效果对比图。图3(c)、(d)、(e)分别是利用Wiener滤波法、BayesShrink方法和改进的LAWML方法对图像去噪后的效果,出现了一定程度图像模糊、部分边缘轮廓辨认困难的现象。图3(f)是采用本文方法的去噪效果,可以看出用本文方法对图像去噪后较好地保持了图像的边缘轮廓特征,且具有较好的视觉效果。
在算法复杂度方面,若图像的大小为N×N,那么Wiener滤波法、BayesShrink方法和改进的LAWML方法的时间复杂度均为O(N2)。本文算法的步骤1)、3)和4)的时间复杂度均为O(N2),步骤2)用到果蝇优化算法求解各细节子带的模型参数,令T0代表果蝇个体一次迭代需要的时间,M为种群数量,K为迭代次数,那么步骤2)的时间复杂度为T=K·M·T0。
在算法耗时方面,由于需要估计出每个细节子带的2D-GARCH(1,1,1,1)模型参数,所以本文算法在计算量上相较于几个对比算法要大一些,但是本系统面向交通的图像处理硬件平台采用的是多核分布式处理器网络以及流水线式的任务分配,所以本文算法并不影响整个系统的实时性。
4 结束语二维GARCH模型是一种新的小波系数统计模型,能够更好地利用小波系数“尖峰厚尾”的分布特性和层内系数间的相关性等重要特性。本文采用果蝇优化算法的极大似然估计来求解2D-GARCH模型参数,完成了对小波系数的准确建模,在此基础上再采用最小均方误差估计原始图像的小波系数,从而得到了一种新的2D-GARCH模型的图像去噪方法。该方法在峰值信噪比和视觉效果上要好于目前一些主流的去噪方法。然而该方法也存在一些需要改进的地方,比如在求解各细节子带的模型参数时存在计算量较大的缺点,今后将在此基础上进一步完善和改进。
| [1] | SIMONCELLI E P.Modeling the joint statistics of image in the wavelet domain[C]//SPIE's International Symposium on Optical Science,Engineering,and Instrumentation.International Society for Optics and Photonics.Denver,USA,1999:188-195. |
| [2] | ANTONIADIS A,BIGOT J,SAPATINAS T.Wavelet estimators in nonparametric regretssion:A comparative simulation study[J].Journal of Statistical Software,2001,6(6):1-83. |
| [3] | DOHONO D L.Denoisingby soft-thresholding[J].IEEE Transactions on Information Theory,1995,41(3):613-627. |
| [4] | CHANG S,YU B,VATTERELI M.Wavelet thresholding for multiple noisy image[J].IEEE Transactions on Image Processing,2000,9(9):1631-1635. |
| [5] | CHANG S,YU B,VATTERELI M.Spatially adaptive wavelet thresholding with context modeling for imaged noising[J].IEEE Transactions on Image Processing,2000,9(9):1522-1531. |
| [6] | CHANG S,YU B,VATTERELI M.Adaptive wavelet thresholding for image denoising and compression[J].IEEE Transactions on Image Processing,2000,9(9):1532-1546. |
| [7] | ACHIM A,BEZERIANOS A,TSAKALIES P.SAR image denoising via Bayesian wavelet shrinkage based on heavy tailed modeling[J].IEEE Transactions on Geoscience and Remote Sensing,2003,41(8):1773-1784. |
| [8] | BOLLERSLEV T.Generalized autoregressive conditional heteroscedasticity[J].Journal of Econometrics,1986,31(3):307-327. |
| [9] | NOIBOAR A,COHEN I.Two-dimensional GARCH model with application to anomaly detection[C]//13th European Signal Processing Conference.Istanbul,Turkey,2005:1594-1597. |
| [10] | AMIRMAZLAGHANI M,AMIRNDAVAR H.Speckle suppression in SAR image using the 2D GARCH model[J].IEEE Transactions on Image Processing,2009,18(2):250-259. |
| [11] | AMIRMAZLAGHANI M,AMIRNDAVAR H.Two novel Bayesian multiscale approaches for speckle suppression in SAR images[J].IEEE Transactions on Geoscience and Remote Sensing,2010,40(7):2980-2993. |
| [12] | PAN W T.A new fruit fly optimization algorithm:taking the financial distress model as an example[J].Knowledge Based Systems,2012,26(2):69-74. |
| [13] | DOHONO D L,JOHNSTONE I M.Ideal spatial adaptati on via wavelet shrinkage[J].Biometrika,1994,81(3):425-455. |
| [14] | LEE J S.Digital image enhancement and noise filtering by use of local statistics[J].IEEE Transactions on Pattern Analysis and Machine Intelligence,1980,2(2):165-168. |
| [15] | 胡海平,莫玉龙.基于贝叶斯估计的小波阈值图像降噪方法[J].红外与毫米波学报,2002,21(1):74-76.HU Haiping,MO Yulong.Method of wavelet threshold denoising based on bayesian esitimation[J].Journal of Infrared and Millimeter Waves,2002,42(9):74-76. |
| [16] | 谢杰成,张大力,徐文立.一种小波去噪方法的几点改进[J].清华大学学报:自然科学版,2002,42(9):1269-1272.XIE Jiecheng,ZHANG Dali,XU Wenli.Several improvements for a wavelet denoising method[J].Journal of Tsinghua University:Science and Technology,2002,42(9):1269-1272. |



