2. 诸暨市联系数学研究所, 浙江 诸暨 311811;
3. 浙江工业大学 之江学院, 浙江 杭州 310024
2. Zhuji Institute of Connection Mathematics, Zhuji 311811;
3. School of zhi jiang, Zhejiang Technology University, Hangzhou, 310024, China
基于文献[1, 2, 3]关于事物的确定性关系与不确定性关系组成一个不确定性子系统的集对分析(set pair analysis,SPA)理论,文献[4, 5, 6]先后借助“白球+黑球”随机试验,向指定区域随机投针试验,掷分币与掷骰子随机试验,说明随机性是事物相互联系的一个属性,随机事件成对存在,在此基础上提出联系概率 (connection probability,CP),(也称“赵森烽-克勤概率” (Zhao Senfeng-Keqin probability,ZKP);论证了无论是古典概型概率(classical probability,CP),几何概型概率 (geometric probability,GP),还是频率型概率 (frequency probability,FP),都可以化为赵森烽-克勤概率ZKP来补充伴随事件的信息作新的研究;文献[7, 8]将赵森烽-克勤概率ZKP应用到风险决策研究得到了新的风险决策模型。习惯上,古典概型概率CP、几何概型概率GP和频率型概率FP统称为“客观概率”(objective probability,OP),因为这三类概率都能用客观上可重复或可大量重复的随机试验验证。但在现实世界中,有些随机现象不能大量重复甚至不能重复,例如远程导弹的精确打击,航天器的成功升空,地外天体探索器的返回,粒子对撞机的建造和正常运行,以及大地震、核泄漏、飞机失事、列车追尾相撞、商厦大火、山体滑坡等等非传统安全问题,对于这类事件,又如何确定相应的概率?在概率论的发展史上和概率的大量实际应用中,人们已有相应的解决办法,这就是与上述“客观概率”相对立的所谓“主观概率(subjective probability,SP)”。历史上,贝叶斯(Thomas Bayes)首先研究了此类概率,所以也称“贝叶斯概率”(Bayes probability,BP),如今,“贝叶斯概率”已得到广泛应用,基于“贝叶斯概率”的不确定性推理已是人工智能的一项重要推理技术[9, 10, 11, 12, 13]。人们会问:对于贝叶斯概率,是否也存在着类似于文献[4, 5, 6]所述的“赵森烽-克勤概率”,贝叶斯公式又能否采用赵森烽-克勤概率加以表达和运算,以开辟出人工智能不确定性推理的新途径,本文试对这一问题作出回答,举例说明贝叶斯概型的赵森烽-克勤概率(Bayes probability-Zhao Senfeng-Keqin probability,BZKP)的应用,并简要讨论贝叶斯概型的赵森烽-克勤概率BZKP的智能化思维特性。
1 贝叶斯概率 1.1 贝叶斯贝叶斯(1702-1763)是英国数学家,创立了著名的贝叶斯概率(BP)和贝叶斯理论(Bayes theory,BT),在统计决策、统计推断和统计估算等方面有重要贡献,促进了现代概率论和数理统计的形成和发展
。 1.2 贝叶斯定义的概率贝叶斯把概率定义为人们根据经验和认识对一个命题的主观信任程度的描述,这种描述用一个在[0, 1]取值的信任函数-置信度表示,显然,这样的概率是一种“主观概率”,在概率统计发展史上,人们把这种“主观概率”称为“贝叶斯概率”。
例如企业开发某新产品,需要预先对该产品在市场上的畅销与否作出判断,由于难以在开发前做大量的随机试验,只能由企业家根据经验和信念作出估计,例如认为畅销的概率是0.8;又如投资家认为“购买某节能环保股票能获得高收益”的概率是0.9;科技人员认为“某课题获得立项”的概率为0.95,肿瘤外科医生根据自己多年的临床经验和一位肿瘤患者的病情估计该患者肿瘤的手术成功可能性是99%,乘坐某航班安全到达目的地的概率是99.999%等,都是人们凭经验、知识或判断能力对所关注事件发生可能性给出的一个信念的度量值,其“主观色彩”昭然若揭,称其为“主观概率”名副其实。
1.3 贝叶斯概率的特性特性1 主观性。 贝叶斯概率的主观性前文已述。历史上,贝叶斯概率的主观性曾遭到一些数学家的批评,认为这种主观的概率确定方法不可取,但贝叶斯概率的广泛和深入应用已经表明贝叶斯概率有一定的客观合理性,这种客观合理性本质上是因为贝叶斯概率具有特性2。
特性2 后验性。 人们事先凭经验、知识或判断能力对所关注事件发生的可能性给出的贝叶斯概率,可以在事后得到验证。例如,事先认为某新产品畅销的概率是0.8,当这一新产品投放市场后,究竟是否畅销就有了客观上的答案;课题立项一旦公布,申报的课题是否立项也明确无疑;航班在飞历了预定的航程后安全到达目的地等。
特性3 不确定性。 贝叶斯概率的不确定性既来自其主观性,如不同的企业家对同一个新产品的市场信任度会不同;也来自其后验结果的不确定性,谁能确切地事先知道一个贝叶斯概率的实际后验结果是必然还是偶然等。
人们会问:贝叶斯概率的不确定性和后验性以及后验值是否可以被一种适当的数学形式(一种“新的贝叶斯概率”)蕴含在其中,从而使得这种“新的贝叶斯概率”是一种“完整的概率”,借此体现出人脑思维的完整性;并进一步借助一定的规则由原先的贝叶斯概率去推知其后验值,借此体现出人脑思维的前瞻性;并且还能用一定的数学形式对应可能出现的各种后验结果,借此体现出人脑思维的灵活性;回答是肯定的,这就是:贝叶斯概率的联系数化,由此引出贝叶斯概型的赵森烽-克勤概率。
2 贝叶斯概型的赵森烽-克勤概率 2.1 原理认识论和人类的社会实践告诉我们,人们对客观事物的认识是一个从知之不多到知之较多、从知部分到全部认知、从片面认识到全面认识、从现象性的表面认识到本质性的深层次认识、从错误认识到正确认识的过程;在这个过程中,对已知部分的认识呈现出相对的确定性,对未知部分的认识呈现相对不确定性;需要在“实践—认识—再实践—再认识”的过程中不断地把“未知”转化为“已知”,据此来减少对于“未知”认识的不确定性;因此,当需要客观地定量刻画和系统地分析人们认知一个事物的全过程时,既需要对已知的相对确定性部分知识作出可置信意义上的刻画,也需要对未知的不确定性部分知识作出置信与否不确定意义上的刻画;并把这两方面的刻画结果反映在同一个数学表达式中,既体现出人脑思维的完整性和灵活性,又便于前瞻地根据“已知”对“未知”展开系统性的分析并作出预见,以体现出人脑思维的前瞻性。这一陈述称之为贝叶斯概率联系数化的基本原理,以下简称原理。
2.2 定义基于以上原理和文献[5]中给出的概率补数定理以及有关集对分析联系数的知识,定义贝叶斯概型的赵森烽-克勤概率如下:
定义1 设P(A)(0≤P(A)≤1)是关于事件A发生与否的一个主观信念值,则称
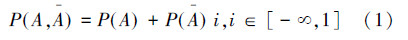
贝叶斯概型的赵森烽-克勤概率也简称贝叶斯概型联系概率或联系概率(contact probability,CP);这是因为式(1)与古典概型联系概率、几何概型联系概率、频率概型联系概率,具有相同的数学形式,并具有以下3条性质:
性质1 P(A)与P(A)的非负性,也就是
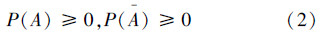
性质2 归一性,也就是

性质3 完备性,也就是
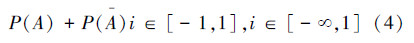
证明 根据P(A)与P(A)的定义可证性质1显然。根据定义1可知P(A)+P(A)=1成立,性质3由于i∈[-∞,1]而成立。
类似于经典概率中的概率三公理,这里把式(2)~(4)称为赵森烽-克勤概率三公理,也就是说,如果有一对随机事件A和A,它们的概率P(A)和P(A)具有以上3条性质,就称其是赵森烽-克勤概率ZKP——一种把随机试验中第一关注事件(主事件)A出现之概率与非第一关注事件(主事件的伴随事件)A出现之概率按关注次序联系在一个数学表达式中的联系概率CP。当然,由此将引出许多需要深入研究的问题。
2.3 转换定理定理 对任意的一个贝叶斯概率,都可以转换为赵森烽-克勤概率ZKP。
证明 根据定义1即可得证。
2.4 后验取值由于式(1)所示的贝叶斯概型的联系概率中,不仅有贝叶斯概率P(A)和P(A)的补数1-P(A)=P(A),而且该补数1-p(A)=P(A)还乘有反映不确定性的系数i,由于i是一个随机转换器,因此可以借助i的数值性质与系统分析,反映出贝叶斯概率可能的后验结果,一般而论,这些结果为以下3种类型。
类型1 衰减型后验
由贝叶斯概型的赵森烽-克勤概率定义可见,在已知贝叶斯概率的情况下写出贝叶斯概率的赵森烽-克勤概率十分简便。例如,前面提到的新产品畅销的概率0.8,按定义1可以改写成0.8+0.2i,当对最坏情况作直接计算时,令i=-1,这时,实际上的畅销概率衰减成0.6;若其间还要考虑“0.8”中受“0.2”与“0.8”的“相互作用影响”这一部分时,则应当先把0.8+0.2i改写成0.64+0.16i+0.2i,再令i=-1,这时,实际上的畅销概率衰减成0.28;如此低的畅销概率,就是不畅销;这种出乎前期主观预料之外、客观上又在市场情理之中的事,在激烈的市场竞争环境中屡见不鲜;类似地可以解释满怀信心投资股市无收益甚至亏损或严重亏损、精心申报的项目不获批、多年相安无事的商厦或厂房突发大火、历年来正常客运的航班突然失联等出乎前期主观预料之外的事件。这里的赵森烽-克勤概率P(A,A)=0.8+0.2i就是这类前期对于事件A有较高主观信念值,事后却出现主观预料之外事件A的一个数学模型,不妨简称此模型为“八二衰减后验模型”或简称“八二模型”;类似地还可以有“九一模型”、“七三模型”等,以对应不同的衰减情况。
衰减型后验可以用以下的不等式表示:
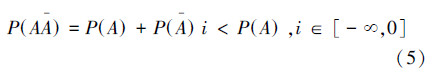
显然,根据赵森烽-克勤概率的性质3可知不等式(5)的左边有可能是负值。例如,设P(A)=0.4,P(A)=0.6,则在i=-1时,P(A)+P(A)i=-0.2,令A为某项目风险投资收益,A为该项目风险投资亏损,P(A)为该项目风险投资收益的概率,P(A)为该项目风险投资亏损的概率,则当P(A)+P(A)i=-0.2时,表明亏损发生,但由于P(A)+P(A)i=0.2 < 1,又说明发生的亏损还不十分严重。
类型2 增益型后验
例如投资获得超预期收益、申报的项目获特批,开发的新产品意外地畅销,这时的i在[0,1]取值。
增益型后验可以用以下不等式表示:
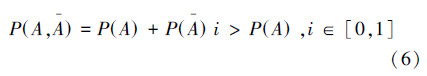
显然,根据赵森烽-克勤概率的性质3可知不等式(6)的左边有可能是接近于1的值。例如,设P(A)=0.75,P(A)=0.25,则在i=0.8时,P(A)+P(A)i=0.95,令A表示某个环保项目风险投资收益,A表示该项目风险投资亏损,P(A)为该项目风险投资收益的概率,P(A)为该项目风险投资亏损的概率,则当P(A)+P(A)i=0.95 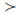 0.75时,表明该项目投资得到超预期收益,原因是该项目实施后,政府加大了对环保项目的政策性补贴,从而使该项目实际收益超过预期。
0.75时,表明该项目投资得到超预期收益,原因是该项目实施后,政府加大了对环保项目的政策性补贴,从而使该项目实际收益超过预期。
类型3 一致型后验
后验值与前期给出的贝叶斯概率一致。一致型后验公式为
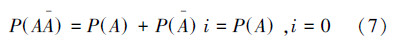
例如,设P(A)=0.98,P(A)=0.02,则在i=0时,P(A)+P(A)i=0.98;令P(A)为某个深海潜水器在某次下海深潜中下潜到预定深度的贝叶斯概率,P(A)为不能下潜到预定深度的贝叶斯概率,则当P(A)+P(A)i=0.98时,表明该潜水器在某次下海深潜中恰好深潜到预定深度。
另一方面看,上面所说的“衰减”,“增益”,“一致”,其实质都是一种“后验”,即由后来的事实验证先前给出的贝叶斯概率,由此可见,贝叶斯概型的赵森烽-克勤概率是蕴含了后验结果和后验值及其不确定性的一种新型概率,是能体现贝叶斯概率后验性和后验结果及其不确定性的一种良好的数学模型。所谓“良好”,是指既满足式(2)所示的归一化要求,又借助随机转换器i在i∈[-∞,1]的不同取值预设了不同方向的后验和后验的不同结果;例如可以是对前期主观概率的一次“简单衰减”,也可以是一次“复合衰减”(计及赵森烽-克勤概率中2个概率相互作用的“衰减”(见本节开头和后面的例2),甚至是“多阶段随机过程的多次简单或多次复合衰减”的后验;也可以是对前期主观概率的一种“增益”性的后验,还可以是对前期主观概率的“一致”性后验。
虽然由已知的贝叶斯概率得出贝叶斯概型的赵森烽-克勤概率简便容易,但采用赵森烽-克勤概率进行贝叶斯公式的计算不是易事,因为涉及到赵森烽-克勤概率的条件概率计算。
3 基于赵森烽-克勤概率的条件概率条件概率是概率论中的一个基本概念[9, 10]。顾名思义,就是在已知一事件(B)发生条件(概率)下计算另一事件(A)发生的概率,记为P(A|B)。
条件概率的计算公式为
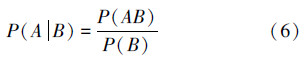
例如,某公司从甲、乙2个生产厂家采购了N个节能灯泡,其中有不合格品,假定情况如表1。
现从N个节能灯泡中任意取一个,考察以下事件:A为“取到次品”,B为“取到甲厂的”,不难得到事件A、B以及AB(取到甲厂生产的次品)的概率如下:
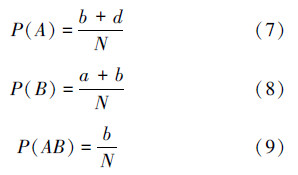
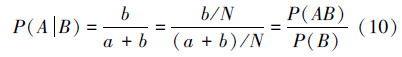
定义2 设A、B为两事件,已知P(B) 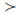 0,则在B发生的条件下A发生的概率为
0,则在B发生的条件下A发生的概率为

要进行赵森烽-克勤概率ZKP意义下的条件概率计算,有2种算法:1)先把式(6)中的各个概率表示成赵森烽-克勤概率:Pc(A)=P(A)+p(A)i的形式,再作赵森烽-克勤概率的运算;2)利用式(6)的结果,把条件概率P(A|B)直接改写成赵森烽-克勤概率:
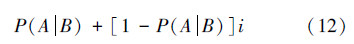
显然,第2种算法简单。但是由第1种算法可以导出用赵森烽-克勤概率表示的条件概率计算公式,并展现出条件概率所蕴含的二次不确定性,说明如下:
先利用式(1)把P(A|B)、P(AB)、P(B)分别改写成赵森烽-克勤概率的形式得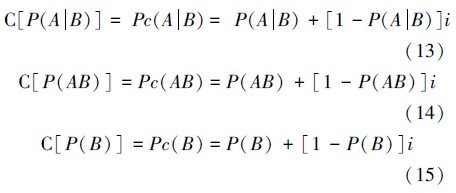
上述C[P(A|B)]、C[P(AB)]、C[P(B)]是把概率P(A|B)、P(AB)、P(B)联系数化的意思,符号“C”是联系数的英译“Connection number”的第一个字母,这里作为“联系数化”的“运算符”使用,不致于引起混淆时,也简称为“C运算”,例如,对条件概率P(A|B)作“C运算”,就是把条件概率P(A|B)联系数化,其具体的算式就是式(13)。
由此得赵森烽-克勤概率意义下的条件概率计算公式:

整理式(16)得

显然,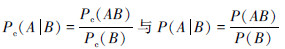
相比,只是在各个“P”的右下角多了一个表示联系概率的下标“c”,式(17)看上去比较复杂,但数值计算过程并不复杂且容易展开分析;特别地,式(17)左边是关于i的二次函数,右边是关于i的一次函数,由此可见赵森烽-克勤概率意义下的条件概率是一个关于i的二次函数,也就是说,条件概率中蕴含着“二次不确定性”,由此决定了赵森烽-克勤概率意义下的条件概率值其实还涉及到对“一次不确定性”和“二次不确定性”的分析;请看后面的例1和例2。
4 贝叶斯公式的赵森烽-克勤定理 4.1 贝叶斯公式贝叶斯公式也称贝叶斯定理,是概率论中的一个重要公式,其表述如下:
设A1A2…An,…是两两互不相容的事件,且有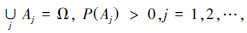 则对任一事件B(P(B)>0)都有
则对任一事件B(P(B)>0)都有
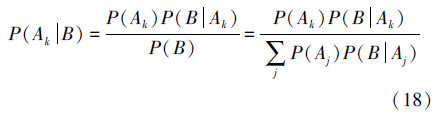
由于式(17)所示贝叶斯公式中的P(Ak|B)是一个条件概率,根据赵森烽等在文献[5]中给出的概率补数定理和前面的论述,可以联系数化得
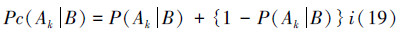


根据第3节,可以称式(18)是贝叶斯公式联系数化的第1种形式,或简称为一次式;式(19)和式(20)是贝叶斯公式联系数化的第2种形式,或简称为二次式;在实际计算中采用何种形式,则根据问题求解需要选取。
5 实例应用例1&NBSP;&NBSP;&NBSP;&NBSP;患病诊断应用[11]
已知某地区居民的肝癌发病率为0.000 4,现用甲胎蛋白法进行普查,医学研究表明,化验结果是有错误的,已知患有肝癌的人其化验结果99%呈阳性(有病),而没患肝癌的人化验结果99.9%呈阴性(无病),现某人的检查结果呈阳性,问1)他真的患肝癌的概率是多少?2)他真的患肝癌的赵森烽-克勤概率是多少?
解:先答(1):记B为事件“被检查者患有肝癌”。A为事件“检查结果呈阳性”,由题设知
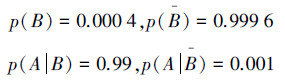
由于现在的目的是求p(BA),由式(17)所示的贝叶斯公式得
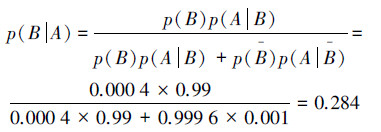
这一结果表明:在检查结果呈阳性的人中,真患肝癌的人不到30%,这个结果使人吃惊,但仔细分析后可以理解,因为肝癌发病率很低,在10 000个人中约有4人,同时有9 996个人不患肝癌。对10 000个人用甲胎蛋白法进行检查,按其错检的概率可知,9 996个不患肝癌者中约有9 996×0.001=9.996(=10)个呈阳性;另外4个真患肝癌的检查报告中约有4×0.99=3.96个呈阳性,仅从13.96个呈阳性中看,真患肝癌的3.96人约占28.4%。
进一步降低错检的概率是提高检验精度的关键。但在实际中,由于技术和操作上的种种原因降低错检的概率又很困难,通常采用复查的方法来减少错误率。比如,对首次检查为阳性的人群再进行复查,这时p(B)=0.284,再用贝叶斯公式计算得
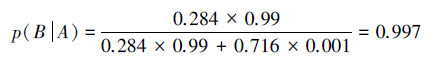
这里把事件B(“被检查者患有肝癌”)看作是“原因”,把事件A(“检查结果呈阳性”)看作是最后“结果”,则用贝叶斯公式在已知“结果”的条件下算得“原因”的概率p(B|A)。
以上是文献[11]中依据经典概率论贝叶斯公式所做的计算。下面答(2)。
由第3节知,要计算该人真的患肝癌的赵森烽-克勤概率有2种思路:
1)根据概率的补数定理,直接把p(B|A)=0.284改写成赵森烽-克勤概率的形式得:
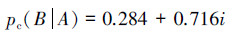
首先是0.284+0.716=1,但由于0.716带有不确定系数i,所以p(B|A)=0.284也带有不确定性;其次是0.716 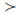 0.284,所以还进一步认为p(B|A)=0.284其实带有较大的不确定性;于是问题转化为如何确定i的值,以便通过i的取值来减少p(B|A)的不确定性,对于这个问题,若仅仅从数量上来看,要让pc(B|A)不再具有不确定性,唯一的办法只有取i=1,这时pc(B|A)=0.284+0.716i=1,但取i=1的物理意义是什么?仅根据pc(B|A)没法作出回答。通过对照问题(1)中的解答知道,取i=1的实际物理意义是“对首次检查为阳性的人群再进行复查”,因为再进行复查后得到的计算结果是:p(B|A)=0.997≈1;事实上,我们在文献[6]中就指出,对于联系概率(赵森烽-克勤概率)中的i,应该把其看作是不确定性系统的特征参数,因其如此,当需要确定一个联系概率(赵森烽-克勤概率中i的数值时,需要对i所表征的不确定性系统作具体的物理分析。
0.284,所以还进一步认为p(B|A)=0.284其实带有较大的不确定性;于是问题转化为如何确定i的值,以便通过i的取值来减少p(B|A)的不确定性,对于这个问题,若仅仅从数量上来看,要让pc(B|A)不再具有不确定性,唯一的办法只有取i=1,这时pc(B|A)=0.284+0.716i=1,但取i=1的物理意义是什么?仅根据pc(B|A)没法作出回答。通过对照问题(1)中的解答知道,取i=1的实际物理意义是“对首次检查为阳性的人群再进行复查”,因为再进行复查后得到的计算结果是:p(B|A)=0.997≈1;事实上,我们在文献[6]中就指出,对于联系概率(赵森烽-克勤概率)中的i,应该把其看作是不确定性系统的特征参数,因其如此,当需要确定一个联系概率(赵森烽-克勤概率中i的数值时,需要对i所表征的不确定性系统作具体的物理分析。
但事物总是一分为二的。在某些情况下,关于联系概率CP中的i仅按定义域取值也有实际意义,见后面的例2。
2)根据式(18)~(20),先把贝叶斯公式中的各个概率联系数化,也就是按概率补数定理进行“C运算”,根据前面给出的题设条件,得
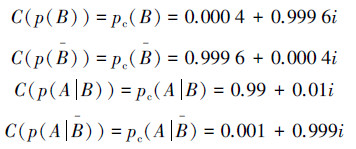

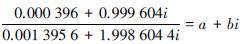
根据文献[4]中的计算方法,可以解得
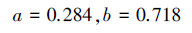

这一结果与前面利用式(17)所示贝叶斯公式得到结果联系数化一致,但等式左边却显示出0.284+0.716i其实是一个二次联系数,也就是说,上述计算过程是一个含有二次不确定(i2)的计算过程。结合题意可知,第一次不确定对应于某地区居民以往的肝癌发病率为0.000 4的不确定性,第2次不确定对应于化验结果存有错误的不确定性,由于某人的这次含有不确定性的检验结果要在以往含有不确定性的医学研究数据基础上才能作出结论,因此该结论具有二次不确定性不足为奇。
由此可见,面对某个随机事件的赵森烽-克勤概率,不仅要对这个概率作“表面分析”(表面上的“数量分析”),还要作“由来分析”,(数字后面的“成因分析”),也就是这个森烽-克勤概率是如何计算得来的分析,经过这二道分析后,才可以判定这个赵森烽-克勤概率是一次(幂)概率还是二次(幂)概率,原因在于赵森烽-克勤概率在计算过程中会应用集对分析理论中给出的以下简化公式:
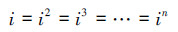
从另一方面看,本例中,同一问题用2种不同的方法(直接把贝叶斯概率公式算得的结果联系数化,与把贝叶斯公式中各概率联系数化后再作运算)求得相同的赵森烽-克勤概率这件事本身也说明上述化简公式的合理性。
贝叶斯公式联系数化所揭示的赵森烽-克勤概率具有二次不确定(i2)还可以从以下的例2得到说明。
例2&NBSP;&NBSP;&NBSP;&NBSP;伊索寓言中孩子与狼的故事。 故事梗概是:一个小孩每天到有狼出没的山上放羊,一天,他在山上喊“狼来了、狼来了”,山下的村民闻声去打狼,到了山上,发现狼并没有来;第2天仍是如此,第3天,狼真的来了,可以任凭牧羊的孩子怎么喊叫,也没有人去救他,因为前2次他撒了谎,村民们不再相信他。
现问:1)如何用贝叶斯公式来分析这个寓言中的村民对牧羊孩可信度的下降;2)如何用贝叶斯概型的赵森烽-克勤概率来分析这个寓言中的村民对牧羊孩可信度的下降;3)分析以上2种思路的异同。
解:首先,记事件A为“孩子说谎”,记事件B为“孩子可信”,不妨设村民们以前对这个孩子的印象为

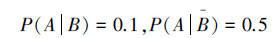
第1次村民上山打狼,狼没来,即孩子说了谎(A),村民根据这个信息,对这个孩子的可信程度改变为(用贝叶斯公式计算得)
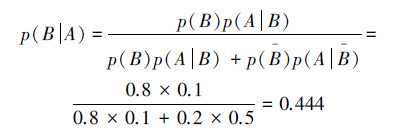
这表明村民上了一次当后,对这个孩子的可信程度由原来的0.8调整为
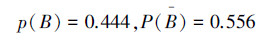
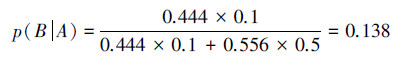
这表明村民经2次上当,对这个孩子的可信程度已经从0.8下降到0.138,如此低的可信度,村民们在听到这个孩子的第3次呼叫时,怎么会再次上山打狼?
以上对试问(1)的解答是文献[11]中给出的,以下是对试问(2)的解答。
参考例1的解答可知:对于试问(2)的解答有2个途径,一是直接把由贝叶斯公式得到的结果联系数化,据此可以把p(B)=0.8与P(B)=0.2用联系概率的形式写成以B为第一关注事件的赵森烽-克勤概率。

根据第2节中的“八二模型”和集对分析关于联系数中确定性(联系分量)与不确定性(联系分量)相互作用理论,上述联系概率中的可信度0.8与不可信度0.2存在相互作用,其相互作用值为0.8×0.2=0.16,此0.16在“最坏情况下”可以看作是“不可信度”在“可信度”中所起的“潜在作用值”,换言之,可信度0.8在此假设下实际上只有0.8-0.16=0.64是可信的,在此基础上再考虑不可信度0.2对可信度0.8的“显在负面作用”,于是得到以下算式及结果:

也就是说,在充分考虑村民对孩子的不信任度0.2对可信度的“直接负面影响”和“潜在负面影响后”,村民们对该孩子的“潜在核心可信度”其实只有0.44。
此0.44与用贝叶斯公式计算得到的0.444仅相差0.004,0.44≈0.444,因为按“四舍五入”法,0.444可以简写为0.44。
村民们在第一次上当后,这种“潜在的核心可信度”得到了一种“证实”和“显化”;也就是有
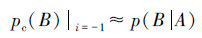
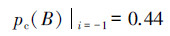
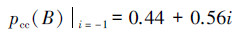
此联系概率(赵森烽-克勤概率ZKP)反映出这时村民们对该孩子的潜在核心可信度其实为0.44+0.56i|i=-1=-0.12,当村民们第2次上当后,上述潜在核心可信度得到一种“证实”和“显化”。根据文献[3, 4]中给出的负概率定义可知,当取B(孩子可信)为参考事件时,pcc(B)可信度=-0.12的物理意义是孩子的话已在0.12程度上判定为是谎言,既然是谎言,村民们在听到这个孩子的第3次呼叫时,自然就不会上山打狼。
以上是“简单衰减”分析,还可以作“复合衰减”分析如下:
首先是仿照本文第2节思路中的“八二模型”,把pc(B)=0.8+0.2i改写成
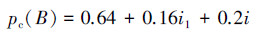
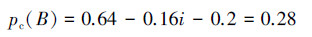
也就是说,在充分考虑村民对孩子的不信任度0.2对可信度的“直接负面作用”和“不信任度与信任度相互作用值0.16的“潜在负面作用后”,村民们对该孩子的“潜在核心可信度”其实只有0.28;显然,这个0.28比用贝叶斯公式计算得到的0.444还要小。
村民们在第一次上当后,这种“潜在的核心可信度”得到了“证实”和“显化”;也就是有

这时再根据概率的补数定理把pc(B)|i=-1=0.28再次联系数化,得


当村民们第2次上当后,上述“潜在核心可信度”得到“证实”和“显化”。根据文献[3, 4]中的负概率定义可知,当取B(孩子可信)为参考事件时,pcc(B)可信度-0.84≈-1的物理意义是孩子的话已被判定为是谎言,既然是谎言,村民们在听到这个孩子的第3次呼叫时,当然就不会上山打狼。
对应于村民们在听到这个孩子的第3次呼叫时没有上山打狼这一事实,这里的“复合衰减”分析比前面的“简单衰减”分析更接近事实。
二是对贝叶斯公式中的每一个概率联系数化后再进行运算,由于篇幅原因,在此略去,有兴趣的读者可以自行试算和分析。
答(3),由上可见,答(1)和答(2)是对孩子与狼的故事从不同角度给出的2种解答,这2种解答的基本假定数据完全相同,但数学处理过程不同,前者纯粹地应用概率论中的贝叶斯公式,后者主要应用赵森烽-克勤概率;所得的计算结果也不同,前者对于村民2次上当后,对孩子的可信度还有0.138,由于0.138>0,根据概率的本义,村民第3次上山打狼的可能依然存在,只是这种可能性已较小(为0.138),但这种可能实际上没有出现,村民没有第3次上山打狼;由此看出,答(2)计算得到的负概率=-0.12更符合村民没有第3次上山打狼这个事实,而其整个计算过程仅涉及到赵森烽-克勤概率中i的2次取负值(i=-1),比起答(1)中的运算简便得多;而从村民没有第3次上山打狼这个事实看,对该问题中的贝叶斯概型的赵森烽-克勤概率作“复合衰减”分析比“简单衰减”分析更接近实际。当然,从贝叶斯概率联系数化的角度看,本问题中的赵森烽-克勤概率就是把孩子的3次呼喊结果都预先蕴含在根据初始条件确定的联系概率pc(B)=0.8+0.2i中,每次呼喊结果无非是对这个联系概率中i每次取i=-1结果的一种验证而已;当然,对于验证结果与实际情况的差异还可以作具体分析,对于同一个问题中的贝叶斯概型的赵森烽-克勤概率是作“简单衰减”分析还是作“复合衰减”分析,也是一个需要进一步研究的问题。
要顺便指出的是,这个故事及其分析在金融界的意义是贷款信用分析,试问,某人向银行贷款,连续2次不还,银行还会第3次贷款给他?在人工智能不确定性推理中的意义是推理结果的可信性分析,试问,某个问题让机器推理,连续2次推理的结果都不可信,还会让机器作第3次推理?如此等等。
6 讨论1)从人工智能的角度看,贝叶斯概率(BP)在本质上是人们利用先前储存在大脑中的经验和知识对随机事件概率的一种推断和估计,这种推断和估计的正确性由随后的客观实践加以验证。本文通过把贝叶斯概率转换为基于集对分析联系数的赵森烽-克勤概率,所得到的贝叶斯概型的赵森烽-克勤概率BZKP,其主要的优越性是把贝叶斯概率的后验可能值预先蕴含在联系数化了的贝叶斯概率(贝叶斯概型的赵森烽-克勤概率BZKP中,借助ZKP中随机转换器i的取值分析,把可能的后验结果分成大于、等于、小于原先给出的贝叶斯概率3种情况,从而把人脑对于一个客观事物从“已知”到“未知”的认识“飞跃”转换成了一个具体的数学公式,既保留了贝叶斯概率的“合理性”,也使贝叶斯概率从“主观”向“客观”的“飞跃”有了“合法性”;“合理性”是指人脑对以往的经验和通过学习得到的知识作出概括并加以量化表述符合情理;“合法性”是指人脑在已有经验和知识的基础上,对“未知”作出带有不确定性的推断分析并加以量化表述符合辩证法关于确定性与不确定性既对立统一又可以在一定条件下相互转化的法则;显而易见,这种“合法性”事实上还涵盖了人脑科学地认知一个客观事物所需要的整体性、前瞻性、灵活性,从而提示贝叶斯概型的赵森烽-克勤概率BZKP实质上是一种智能型概率(intelligence probability,IP)。至于如何对这种智能型概率IP展开具体计算和分析,乃至调控“i”,则是一个有待深入研究的课题。
2) 可以认为:人脑之所以具有“智能”或者“智慧”,一是由于人脑的思维具有整体性,“人无远虑,必有近忧”、“居安思危”、“知己知彼,百战不殆”等成语,就是说人脑思维具有整体性的特点;特别是训练有素的人脑思维,其思维的整体性尤为显著。二是人脑的思维具有前瞻性,所谓“举一反三”、“深谋远虑”、“一叶知秋”、 “见微知著”、“以此类推”等等,就是说人脑能够依据已有的知识自动地对“未知”进行前瞻性推理。三是人脑的思维具有灵活性,正是灵活性,才使得人们能够不断适应环境的变化,原始人随着环境的变化而进化,现代人也同样如此;这种灵活性也可以称为不确定性。由于迄今为止对人脑思维的物理机制和化学机制还没有完全搞清,因此,从数学的角度给出人脑思维的模型不失为是一种经济且有效的途径,也是人工智能的题中之义。换言之,人脑一旦就某事物的“已知”部分作出量化表达,如贝叶斯概率,需要同时对“未知”部分也作出量化表达,正是在这一个意义上,贝叶斯概率联系数化成为必要。由于“未知”部分对于“已知”部分通常具有不确定性,因此对于“未知”部分作出量化表达时需要有不确定性标记,赵森烽-克勤概率中的i担当了这一角色。这也是我们把贝叶斯概率联系数化,转换成赵森烽-克勤概率的一个初衷。
3)贝叶斯概型的赵森烽-克勤概率BZKP虽然从数学形式上保持了与客观概型联系概率OP(古典概型概率联系概率CP、几何概型概率联系概率GP、频率型概率联系概率FP)的一致性,但两者仍有不同之处:3种客观概型的赵森烽-克勤概率OZKP侧重从空间的维度补充了经典概率的即或概率信息,也就是非第一关注事件的信息;贝叶斯概型的赵森烽-克勤概率BZKP侧重从时间的维度补充贝叶斯概率的即或概率信息(也就是非第一关注事件的信息,也可以说是第一关注事件的后验信息),但其时长要大大超过客观概率OP的即或概率的信息时长,这一点也有待深入研究;由于客观事物的动态不确定性通常寄寓在时间中,空间的遍历通常无法抵消由时间流逝带来的不确定性,因此,贝叶斯概型的赵森烽-克勤概率BZKP是一种比客观概型赵森烽-克勤概率OZKP更为复杂的一种联系概率CP,本文中的2个应用实例已从应用层面上揭示出这种复杂性,例如其中含有二次不确定或者多次不确定以及不同次不确定的迁移或递进,这也是可以称其为是智能型概率IP的一个理由;由于贝叶斯推理是现有人工智能进行不确定性推理的一项重要推理技术,如何把已有的基于贝叶斯概率(BP)的不确定性推理扩展为基于赵森烽-克勤概率(ZKP)的不确定性推理,因此是一项复杂和困难的工作,也是令人感兴趣和内容丰富的工作。
4)本文基于人脑思维的整体性、前瞻性和灵活性假设,研究贝叶斯概率的后验值与贝叶斯概率的关系,得到的贝叶斯概型的赵森烽-克勤概率(BZKP)在数学形式上与古典概型的赵森烽-克勤概率(CZKP)、几何概型的赵森烽-克勤概率(GZKP)和频率型赵森烽-克勤概率(FZKP)完全一致,这一点令人惊讶;它从一个侧面说明了在文献[4, 5, 6]中提出的新的随机摸球试验、新的随机投针试验、新的掷硬币与掷骰子试验,不仅仅是一种客观上的可演示的数学物理实验,其实还是一种如本文所说的智能思维实验的数学物理模型;也不仅仅说明本文给出的人脑思维的整体性、前瞻性和灵活性假设可以有相应的随机试验作为其数学物理背景,有相应的数学模型,也从一个侧面说明了集对分析联系数思想内涵的深刻性。特别要指出的是:人脑思维的整体性、前瞻性和灵活性不是每一个个体人脑所必定具有,一般说来,只有经过特定教育和训练的特殊个体人脑,或者是某个群体的人脑之和才具有;为此,需要引进智脑的概念,不妨定义智脑是同时具有思维整体性、思维前瞻性、思维灵活性以及思维现实性、思维经济性等诸多优良特性的智能脑(intelligent brain,IB),贝叶斯概型的赵森烽-克勤概率BZKP则是智脑IB的一个特征参数;有关赵森烽-克勤概率与智脑思维现实性、经济性等方面的关系,也有待进一步研究。
5)本文把联系数化后的贝叶斯概率定义为赵森烽-克勤概率,而不再简称为联系概率CP,原因之一是为了在形式上与贝叶斯概率BP这个名词术语相对应,但又作明显区别;原因之二是概率论有用新概念(新算法、新定理)提出者命名这个新概念(新算法、新定理)的习惯做法,如贝努利试验、契比雪夫不等式、马尔可夫链、高斯分布、等等(其中馬尔可夫链就是当年的馬尔可夫在硕士论文中自己命名的);原因之三是贝叶斯概率联系化得到的联系概率BZKP与古典概型CP、几何概型GP、频率概型FP联系数化得到的联系概率形式相同但实质内容不同。概而言之,在涉及到古典概型概率CP、几何概型概率GP和频率型概率FP联系化的情况下采用联系概率CP这个称谓,但在把贝叶斯概率联系数化时,采用赵森烽-克勤概率这个称谓较为贴切;在不需要特别说明的情况下,把古典概型联系概率CCP、几何概型联系概率GCP、频率概型联系概率FCP、贝叶斯概型联系概率BCP统称为赵森烽-克勤概率符合概率论的习惯,也便于应用。原因之四是在汉语中,“联系”一般作动词用,但根据“联系概率”的定义,它是一个专用的名词,把联系概率称为赵森烽-克勤概率就自然地避免了上述误解;原因之五也是提出者对于概率论创新可能引起非议的一种担当和承受(历史上,贝叶斯概率在提出时也曾受到人们的批评和非议);由于概率论已有300多年的发展史,概率是概率论中最为基础性的一个概念,但在文献[4, 5, 6, 7]中,基于集对分析理论(SPT)和对一系列新的随机试验结果作客观而深入的思考后引入联系概率CP的概念,无疑是对于概率概念的一个创新,由此引出的一些新概念已为构建一个新的概率论提供了必要的准备。
6)从联系数的角度看,贝叶斯概型的赵森烽-克勤概率BZKP也是一种概率意义下的联系数,这从一个侧面说明了联系数内涵的丰富性,有关联系数方面的知识可以参考文献[14, 15, 16]等。
7)从集对的角度看,贝叶斯概型的赵森烽-克勤概率BZKP是人们已有知识(集)与未知知识(集)组成的一个集对,对于这个概率的全部分析,也因此是一种集对分析,如何把集对分析的已有理论方法应用到赵森烽-克勤概率的计算和分析上,也是一个需要进一步研究的课题。
8)从辩证法和联系科学的角度看,贝叶斯概型的赵森烽-克勤概率BZKP把已知与未知联系,主观与客观联系、确定与不确定联系、历史与未来联系、简单与复杂联系、局部与整体联系、静态与动态联系,因此也是关于事物联系的一种数学模型,是辩证法和联系科学研究的一项内容[17, 18],对此也需要深入研究。
7 结束语本文基于集对分析和联系数理论以及作者已有工作基础上,研究贝叶斯概率与其后验值的关系及其联系数表述,定义了贝叶斯概型的赵森烽-克勤概率BZKP,给出了贝叶斯概率BP向联系概率CP转换定理,举例说明贝叶斯概型的赵森烽-克勤概率(BZKP的实际应用,通过讨论贝叶斯概型的赵森烽-克勤概率BZKP与古典概型联系概率CCP,几何概型联系概率GCP,频率型概率联系概率FCP的形式一致性和内涵差异性,指出了贝叶斯概率联系数化的重要意义不仅把主-客观概率统一起来,更在于给出了人脑从已知推导未知思维的一种数学模型和给出智脑IB的概念:智脑IB是具有思维整体性、思绪前瞻性、思维灵活性、以及思维现实性、思维经济性、等优良特性的智能脑,贝叶斯概型的赵森烽-克勤概率BZKP则是这种智脑的一个特征参数,从而为脑科学研究和人工智能中的贝叶斯推理研究开辟了新的途径……;所有这些工作,都有大量需要进一步研究的问题,我们将在后续论文中继续讨论相关问题,也期待有兴趣的专家学者与我们共同致力于这方面的探索和研究.
| [1] | 赵克勤,宣爱理.集对论--一种新的不确定性理论方法与应用[J].系统工程,1996,14(1):18-23.ZHAO Keqin,XUAN Aili.Set pair theory-a new theory method of non-define and its applications[J].Systems Engineering,1996,14(1):18-23. |
| [2] | 赵克勤.集对分析及其初步应用[M].杭州,浙江科技出版社,2000:44-64. |
| [3] | 赵克勤.集对分析的不确定性理论在AI中的应用[J].智能系统学报,2006,1(2):16-25.ZHAO Keqin.The application of uncertainty systems theory of set pair analysis (SPA) in the artiartificial intelligence[J].CAAI Transactions on Intelligent Systems,2006,1(2):16-25. |
| [4] | 赵森烽,赵克勤.概率联系数化的原理与联系概率在概率推理中的应用[J].智能系统学报,2012,7(3):200-205.ZHAO Senfeng,ZHAO Keqin.The principle of the probability of connection number and application in probabilistic reasoning[J].CAAI Transactions on Intelligent Systems,2012,7(3):200-205. |
| [5] | 赵森烽,赵克勤.几何概型的联系概率与概率的补数定理[J].智能系统学报,2013,8(1):11-15.ZHAO Senfeng,ZHAO Keqin.Contact probability (complex probability) of Geometry probability and probability of the complement number theorem[J].CAAI Transactions on Intelligent Systems,2013,8(1):11-15. |
| [6] | 赵森烽,赵克勤.基于联系概率与随机事件的转化定理[J].智能系统学报,2014,9(1):53-69.ZHAO Senfeing,ZHAO Keqin.Frequency type contact probability and random events transformation theorem[J].CAAI Transactions on Intelligent Systems,2014,9(1):53-69. |
| [7] | 赵森烽,赵克勤.联系概率的由来及其在风险决策中的应用[J].数学的实践与认识,2013,43(4):165-171.ZHAO Senfeng,ZHAO Keqin.The contact probability in risk decision-making medium application[J].Mathematics in Practice and Theory,2013,43(4):165-171. |
| [8] | 赵森烽,赵克勤.基于赵森烽-克勤概率的新型风险决策[M].北京:知识产权出版社,2013:186-192. |
| [9] | 王梓坤.概率论基础及其应用[M].北京:科学出版社,1979:218-219. |
| [10] | 赵秀恒,米立民.概率论与数理统计[M].北京:高等教育出版社,2008:1-28. |
| [11] | 茆诗松,程依明,濮晓龙.概率论与数理统计教程[M].北京:高等教育出版社,2012:49-50. |
| [12] | 李德毅.不确定性人工智能[M].北京:科学出版社,1979:218-219. |
| [13] | 蔡自兴,徐光佑.人工智能及其应用[M].北京:清华大学出版社,2010:114-116. |
| [14] | 赵克勤.二元联系数A+Bi的理论基础与基本算法及在人工智能中的应用[J].智能系统学报,2008,3(6):476-486.ZHAO Keqin.The theoretical basis and basic algorithm of binary connection A+Bi and its application in AI[J].CAAI Transactions on Intelligent Systems,2008,3(6):476-486. |
| [15] | 赵克勤.联系数学的基本原理及应用[J].安阳工学院学报,2009,8(2):107-100.ZHAO Keqin.The basic principle and application of Connection Mathematics[J].Journal of Anyang Institute of Technology,2009,8(2):107-110. |
| [16] | 赵克勤,赵森烽.奇妙的联系数[M].北京:知识产权出版社,2014:1-200. |
| [17] | 赵克勤.自然辩证法有数学模型吗?[N].自然辩证法报,1988-05-10(3).ZHAO Keqin.Dialectics of nature,amathematical model fot it,Report of the dialectics of nature,1988,1988-05-10(3). |
| [18] | 赵克勤.自然辩证法可以称为联系科学吗[J].自然辩证法通讯,2008,53(6):99-101.ZHAO Keqin.Dialectics of nature can be called the connection science?[J].Journal of Dialectics of Nature,2008,53(6):99-101. |



