2. 哈尔滨工业大学 控制理论与制导技术研究中心, 黑龙江 哈尔滨 150001
2. Center for Control Theory and Guidance Technology, Harbin Institute of Technology, Harbin 150001, China
利用巡视车在星球的表面实地考察是我国未来深空探测计划的重要任务,为了保证巡视车能够适应星球的低重力环境保证勘探任务顺利进行,在地球表面模拟低重力效果进而测试巡视车动力性能成为了一项不可缺少的环节[1]。
模拟低重力的传统方法有气浮法、配重法、主动悬吊法等。其中文献[2, 3]提出的气浮法主要应用于二维平面内的模拟,对于巡视车所需要进行的爬坡测试等其模拟效果并不理想。对此文献[4, 5]提出引入配重块抵消重力方法以实现三维空间的测试,但由于系统中缺少主动控制,对于路面颠簸给低重力模拟系统带来的竖直方向干扰,系统的抑制效果不好。对此文献[6, 7, 8, 9]提出了电机与弹簧协同工作的主动悬吊法,为了减少转轴上摩擦力矩影响,该方法采用“内-外环路设计方法”先将力矩电机自身闭环在速度内回路后,利用电机收放绳索的速度对外环的吊索张力进行控制,其中速度回路设计的依据是将带宽提高到力回路的5倍以上,以实现与后续力回路设计的解耦;然而速度回路在力回路中有阻尼作用,速度回路带宽的提高会带来力回路控制精度的下降,平衡内环速度回路的带宽增加了系统设计难度,并且文献[7, 8]均没有考虑等效弹性系数的不确定性和系统延时对于鲁棒稳定性的影响。
本文在主动悬吊法的基础上改变整体的控制方案,采用利用力矩电机直接对力回路进行控制的方式,避免对速度回路的设计,并在滚筒处加装码盘引入位置控制;针对转轴的摩擦转矩及巡视车竖直方向加速度干扰,采用H∞控制方法对系统进行综合,同时解决了系统的参数不确定性与系统延时对于鲁棒稳定性的影响。通过在xPC Target实验平台进行的硬件在环实验,结果表明控制器对于上述问题具有良好的抑制能力,并且低重力模拟系统的控制精度得到了保证。
1 系统数学模型的建立用于为巡视车模拟竖直方向低重力环境的恒张力子系统结构如图1,它主要由缓冲机构与电机部分组成,其中为了方便后续说明,在图1中设缓冲机构的横纵支架的中心轴线分别为ox1与oy1,摆杆所在中心轴线为ox2,o点为3条轴线交点。为了保证巡视车所受低重力环境在巡视车上下颠簸时保持恒定,需要对吊索张力T进行调节,使其稳定在平衡位置θ=0时的吊索张力T0上。文献[7]中已对缓冲机构工作原理做出了详细说明,并推导出缓冲机构与吊索张力T关系为
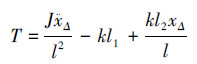
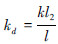 ,等效质量md=
,等效质量md=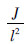 ,设T距离T0的偏差项为ΔT,则有
,设T距离T0的偏差项为ΔT,则有
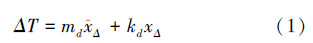
 |
| 图 1 恒张力子系统结构图Fig. 1 The structure diagram of the constant tension subsystem |
令l′为平衡位置距巡视车的吊索长度,xd为巡视车竖直方向的位移,xu为吊索收放长度,由吊索长度关系可得
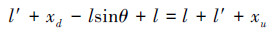
整理得


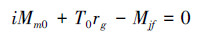
当巡视车出现扰动时电机在Mm0基础上输出力矩为MmΔ,减速器的动摩擦力矩折算到减速器输出轴为Mdf,电机转子、减速器、滚筒三者的转动惯量折算到减速器输出轴为Jd,对减速器输出轴建立转动方程:

由于系统工作时减速器摩擦力矩具有谱宽且动静状态不定的特点,因此将动静摩擦力矩统一用Mf表示,低重力模拟系统为对力的偏差ΔT的调节型系统,可将式(4)中的平衡位置剔除掉得到
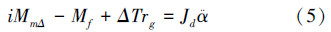
对于式(1)与式(5)体现的缓冲机构和电机对于ΔT控制的耦合问题,可以将式(1)视为对ΔT的观测方程;并将式(1)、式(2)和式(3)代入式(5),将电机对力的控制转化为电机对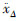 的控制易实现2部分的解耦:
的控制易实现2部分的解耦:
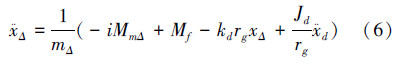

在式(7)中可以得出通过对滚筒转角的测量从而引入位置反馈通道可以提高系统对于巡视车竖直方向干扰以及减速器摩擦力矩干扰的抑制,有助于系统的精确控制。
低重力模拟系统中力矩电机采用为交流伺服电机,由于从其内部结构上推导数学模型较为复杂且本文并不主要研究电机结构,因此可采用实验对其进行参数辨识,利用电机自带的扫频功能,辨识得到电机的等效模型:
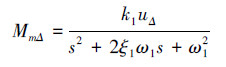
选取状态变量x1=MmΔ,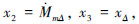
 输出量为y1=ΔT,y2=α,干扰量为
输出量为y1=ΔT,y2=α,干扰量为 、Mf,控制量为uΔ,由上述关系建立系统标称模型为
、Mf,控制量为uΔ,由上述关系建立系统标称模型为
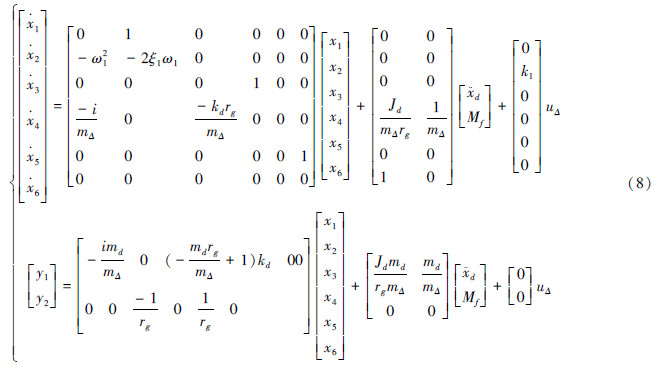
低重力模拟系统工作在平衡位置时弹簧已处于拉伸状态并为吊索张力T0提供平衡拉力,系统正常工作时吊索张力波动量ΔT不超过10 N,这对于本就处于拉伸状态且弹性系数达到数千N/m弹簧来说,此时弹簧的拉力对于ΔT变化做出的微小的伸缩不再严格遵循胡可定律,通过实验测得这种变化会导致等效弹性系数kd有ω0=5%的波动,为了保证系统的鲁棒稳定性,模型建立是需将其不确定性考虑在内。
另一个影响系统鲁棒稳定性的问题是系统存在的延时问题,由于采用串口通信的方式对电机进行控制,而串口通信时的传递位数有限,这会使得系统控制指令约有0.5 ms的延时才能到达电机,并且由于控制器在定时时间为1 ms的定时器中断处理函数内进行控制指令计算,使得相关采集的数据最高可能等待1 ms才能转化为控制指令,再考虑到控制器运算时间及系统的其他未建模特性,因此判断系统延时时间最高为2 ms[11]。为了便于后续控制器设计时对其进行处理,将其建立在系统建模中。
延时问题可理解为控制器的输出在进入对象前存在延时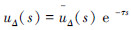 ,由于只知道延时可能的最大时间,采用乘性不确定表达延时问题,设
,由于只知道延时可能的最大时间,采用乘性不确定表达延时问题,设

式(9)左端为乘性不确定性的标准形式[10],其中满足式(9)的L(s)为待求解的不确定性,它在式(9)中的含义可理解为 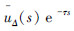 为偏离
为偏离  的相对值,即
的相对值,即
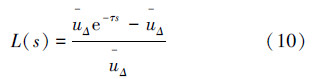
因此接下来需要求解L(s)。令l(s)为 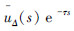 偏离
偏离  的相对值界限,则L(s)=l(s)Δ1,|Δ1|≤1,而当延时取最大值0.002s时,
的相对值界限,则L(s)=l(s)Δ1,|Δ1|≤1,而当延时取最大值0.002s时,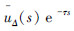 最为偏离
最为偏离  ,此时可以得到l(s),因此将τ=0.002s代入式(10)得到
,此时可以得到l(s),因此将τ=0.002s代入式(10)得到
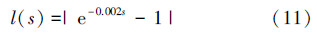
因此结合式(9)、(11),无法准确测得的延时问题转化为
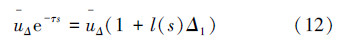
为了减少非线性环节对控制器设计带来的难度,利用e-τs-1泰勒展开一次项将式(11)中的l(s)表示为l(s)=0.002s,式(12)可由图2表示。
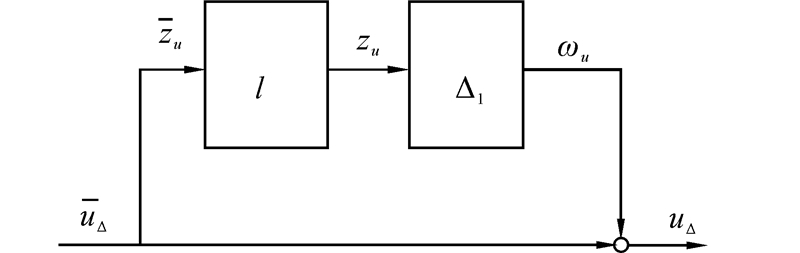 |
| 图 2 乘性不确定性表示延时问题Fig. 2 Multiplicative uncertainty said the delay problem |
 ,|Δ0|≤1代入式(8),并引入
,|Δ0|≤1代入式(8),并引入 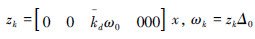 。
为了将不确定性Δ1与标称模型分离,在图2中引入输入项ωu与输出项
。
为了将不确定性Δ1与标称模型分离,在图2中引入输入项ωu与输出项 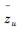 ,将l视为对
,将l视为对 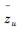 的加权项,将
的加权项,将 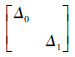 视为Δ,代入系统模型中得到:
视为Δ,代入系统模型中得到:
控制算法需要结合被控对象的特点来设计,考虑低重力模拟系统工作时所受干扰情况以及建模过程中系统本身存在的问题,可以总结低重力模拟系统具有如下特点:
1) 巡视车工作时路面颠簸,通过实验测得系统受到幅值为-0.7~0.7 m/s2,频率最高为5 Hz的巡视车竖直方向加速度 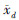 的干扰。
的干扰。
2)由于减速器摩擦力矩Mf数值较高且谱很宽,因此对系统的稳定性及控制精度产生很大影响。
3)系统缓冲机构中存在等效弹性系数参数kd不确定性,系统存在已转化为乘性不确定性的延时问题。
H∞控制算法为鲁棒控制中的一种,它的最大特点以系统的干扰和不确定性为基础来设计控制器,将系统存在干扰及不确定性问题统一转化为系统的被调输入与被调输出,并通过小增益定理保证了被调输入输出间的无穷范数小于1时系统的鲁棒稳定性,因此低重力模拟系统采用H∞控制算法[10]。
为了方便计算H∞控制器,将系统控制结构框图如图3转化为H∞标准结构如图4。
 |
| 图 3 系统控制结构框图Fig. 3 The block diagram of control system |
 |
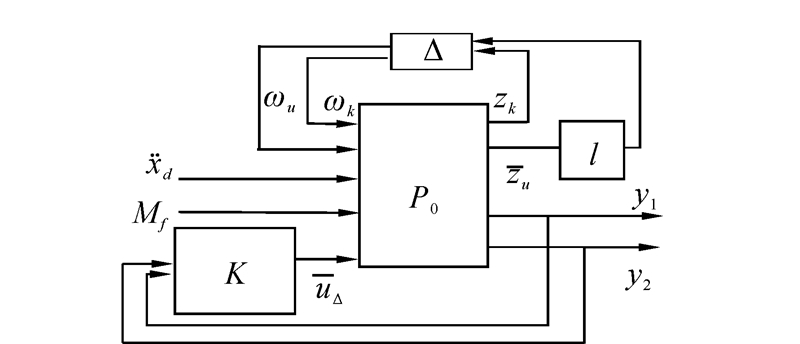
| 图 4 H∞控制的标准形式Fig. 4 The standard structure of the H∞controller |
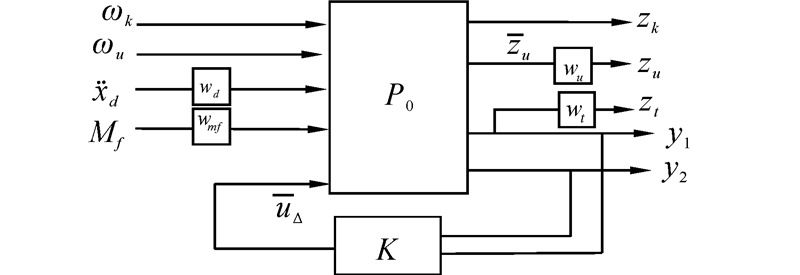
wd、wmf、wt、wu分别为待设计的表述系统特性的加权函数,而zt为系统性能的评价输出。H∞控制算法将基于被调输入 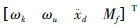 到被调输出
到被调输出  的传递函数的无穷范数来设计控制器。
的传递函数的无穷范数来设计控制器。
首先设计系统加权函数,wd与wmf作为输入加权函数,在H∞控制的标准形式中分别为巡视车竖直方向加速度与减速器的摩擦力矩做加权输入。wd与wmf的作用为调整控制器对于 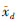 与wmf的抑制力度,因为
与wmf的抑制力度,因为 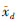 的数值最高为0.7,而wmf的数值最高为3,2个干扰源在数量级上有所差别,为了对不同数量级的干扰做出针对性的抑制,因此设计wd=0.7,wmf=3,使得控制器对干扰的抑制更有针对性。
的数值最高为0.7,而wmf的数值最高为3,2个干扰源在数量级上有所差别,为了对不同数量级的干扰做出针对性的抑制,因此设计wd=0.7,wmf=3,使得控制器对干扰的抑制更有针对性。
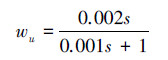
wt为决定控制精度ΔT的加权函数,它的作用是在巡视车工作频率段f≤5Hz,降低巡视车干扰对吊索拉力变化量影响,而对工作频段外幅频特性可能的升高不做限制,因此设计wf为低通滤波器形状传递函数,并将转折频率设为5Hz,而幅值在满足小增益定理的基础上尽量增高以惩罚各干扰因素对ΔT的影响,取幅值为0.6,即
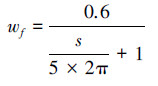
对于H∞控制器求解方法较为繁琐且步骤相对固定,可通过Matlab软件的hinfric函数求解,并且hinfric函数实现在各阶控制器中寻优,所以优化效果较好。代入各变量值i=5,ξ1=0.6,k1=4.373 6×106,ω1=628,kd=1 552 N/m ,rg=0.1 m,md=8.5 kg,Jd=20 kg·m2。通过编程求得此时的控制器如式(14),系统的最优指标为1.016 6,即综合后的系统满足小增益定理,控制器保证了系统的鲁棒稳定。
从ΔT到  传递函数:
传递函数:

 传递函数:
传递函数:

为了验证控制器的有效性,本文采用xPC Target实验平台实现硬件在环实时检测,xPC Target采用了宿主机—目标机的技术途径,宿主机用于运行Simulink及其工具包,目标机则对底层硬件进行操作[12-18]。xPC Target实验平台具有模块化、可靠性高、成本低廉的优势,因此广泛应用于工业生产的测试与产品研发[19-24]。低重力模拟系统在xPC Target实验平台的实现框图如图5。实验目标:在巡视车处于静止、颠簸与越障3种状态下,保持吊索张力为53.5 N来为迷你巡视车提供低重力环境,并检验控制器效果。在图6~8中可以看到对于系统存在参数不确定及延时问题,控制器均保证了低重力模拟系统的鲁棒稳定。
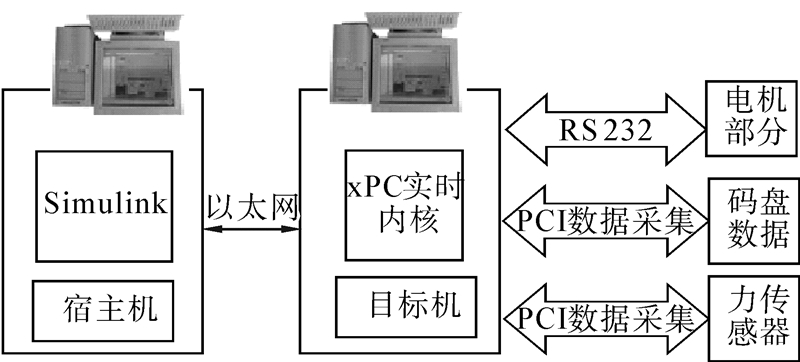 |
| 图 5 xPC Target实验平台的实现框图Fig. 5 The diagram of xPC Target experiment platform |
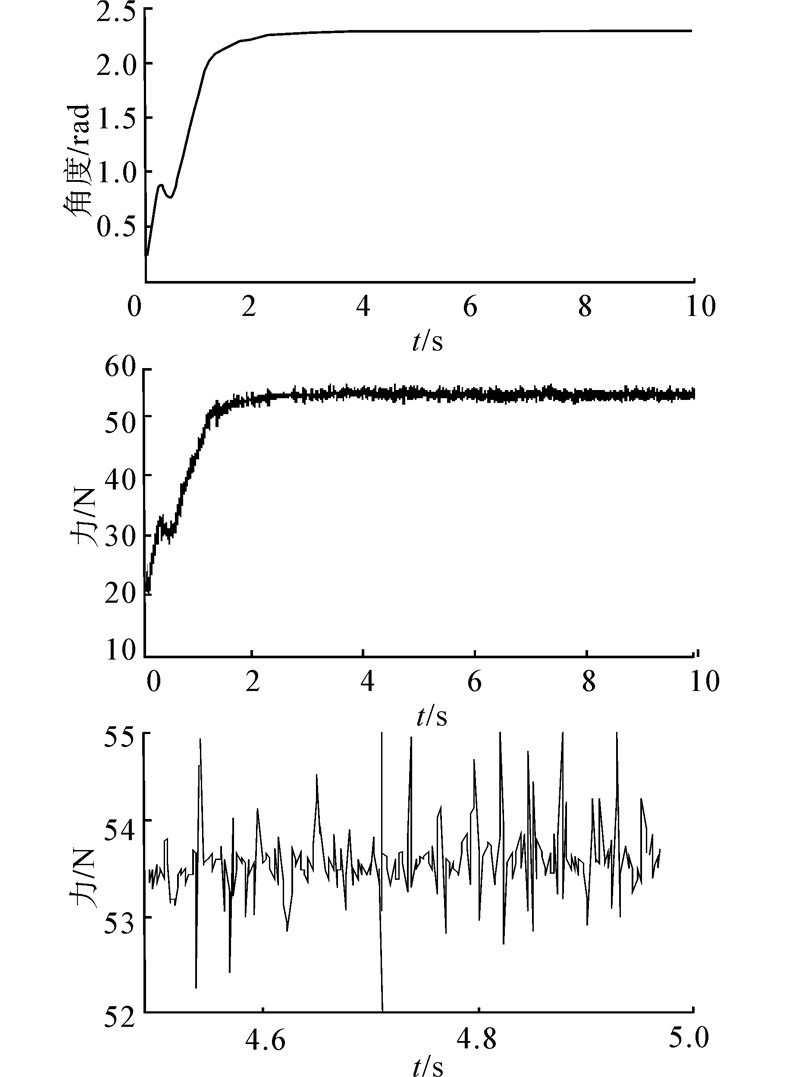 |
| 图 6 巡视车吊起后的静止状态Fig. 6 Stationary state of the lunar rover |
 |
| 图 7 巡视车经过颠簸路面的状态Fig. 7 The state of the lunar rover on the bumpy road |
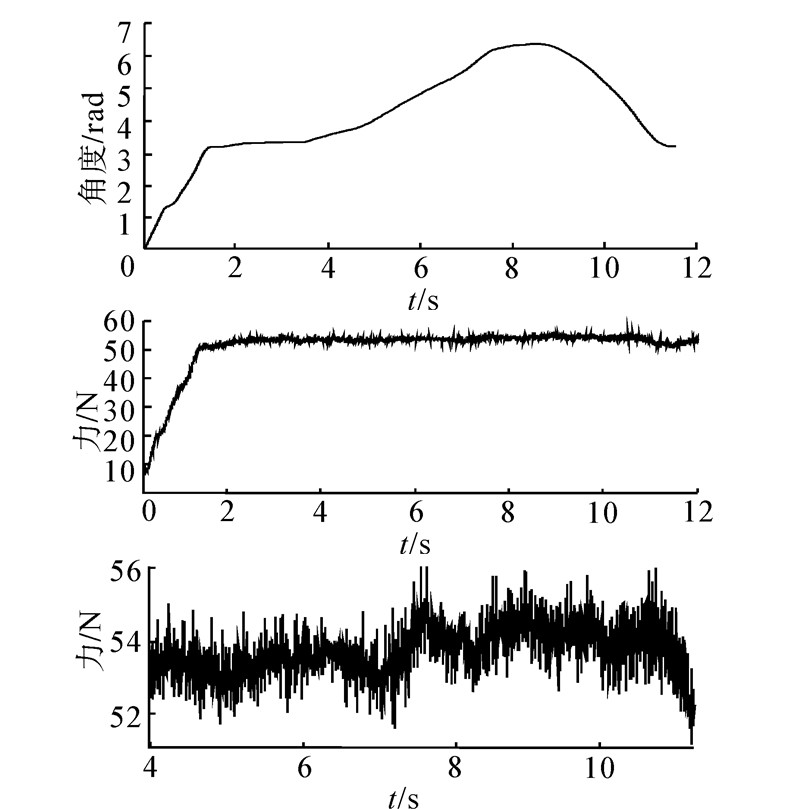 |
| 图 8 巡视车越障的状态Fig. 8 The state of the lunar rover getting over the obstacle |
在图6为巡视车被吊起后处于静止状态。可以看到电机在提起巡视车的过程中,经过3s时达到平衡点;为了保证安全,对电机的控制指令做出了限幅,因此整个吊起巡视车的过程相对平缓,并未出现超调;平衡时吊索张力为53.5±1.5 N,实现了巡视车的低重力状态模拟。
图7为巡视车经过颠簸的路面。由图7(a)可得路面的颠簸幅值约为(2.5-2.4)×0.1=0.01 m,并且在巡视车上下颠簸的频率较高时,吊索张力保持在53.5±3 N。
图8为巡视车跨越障碍。图8(a)中可以判断,障碍高度约为(6.2-3.2)×0.1=0.3 m,上坡时间约为4 s,下坡时间约为3 s;图8(b)中吊索拉力保持在51~56 N,上坡时的吊索拉力误差保持在1.5 N以内,而进入下坡时,在8~10 s内吊索张力变化达到2.5 N,这是由于此时加速度较大导致动态误差增大,随着坡度变缓,巡视车竖直方向加速度减小,因此10~11 s吊索张力误差逐渐减小。
综上,低重力模拟系统的吊索张力最大动态误差为3 N,即吊索张力的精确度达到94.4%,实现低重力模拟系统的精确控制。
4 结束语本文针对巡视车测试时传统主动悬吊方式模拟低重力方法存在的速度回路带宽与力控制精度难以平衡的问题,提出直接对力回路控制并加入位置控制的控制方案;在建立系统数学模型过程中考虑了参数不确定性与转化为乘性不确定性的延时问题,实现了不确定性的分离;根据系统存在巡视车测试时竖直方向干扰、减速器摩擦转矩及系统自身的不确定性设计了H∞控制器。通过xPC实验平台的检验,本文提出的控制方案保证了系统的控制精度,并且有效抑制系统所受到干扰以及自身不确定性与延时问题,为低重力模拟系统的进一步完善提供了理论依据。
| [1] | 肖福根,叶培建.月球探测工程中的月球环境问题[J].航天器环境工程,2006,23(1):1-3.XIAO Fugen,YE Peijian.Issues about lunar environment in lunar exploration project[J].Spacecraft Environment Engineering,2006,23(1):1-3. |
| [2] | ROBERTSON A,INALHAN G,HOW J P.Formation control strategies for a separated spacecraft interferometer[C]//American Control Conference.Palo Alto,America,1999:4142-4147. |
| [3] | XU Y,BROWN B,AOKI S,et al.Mobility and manipulation of a light-weight space robot[J].Robotics and Autonomous Systems,1994,13(1):1-12. |
| [4] | BROWN H,SOLO S.A novel gravity compensation system for space robot[C]//ASCE Specialty Conference on Robotics for Challenging Environments.Albuquerque,USA,2000,5(3):250-253. |
| [5] | SATO Y,EJIRI A,IIDA Y,et al.Micro-G emulation system using constant-tension suspension for a space manipulator[C]//IEEE International Conference on Robotics and Automation.Piscataway,USA,1991:1893-1900. |
| [6] | WHITE G C,XU Y S.An active vertical-direction gravity com-pensation system[J].IEEE Transactions on Instrumentation and Measurement,1994,43(6):786-792. |
| [7] | 王连明.低重力模拟系统控制算法的研究[D].哈尔滨:哈尔滨工业大学,2010:10-30.WANG Lianming.Research on control algorithm of microgravity simulating system[D].Harbin:Harbin Institute of Technology,2010:10-30. |
| [8] | 王乐.低重力模拟器吊索张力控制算法研究[D].哈尔滨:哈尔滨工业大学,2011:11-20.WANG Le.Control algorithm on the sling tension of low-gravity simulating system[D].Harbin:Harbin Institute of Technology,2011:11-20. |
| [9] | 李灏,徐志刚,郭渝萍.月球巡视器吊点张力控制系统的设计[J].机械设计与制造,2012(4):50-52.LI Hao,XU Zhigang,GUO Yuping.Design of suspension point tension control system for lunar rover[J].Machinery Design&Manufacture,2012(4):50-52. |
| [10] | 刘志康,姚郁.线性鲁棒控制[M].北京:科学出版社,2013:267-300. |
| [11] | 刘复华.8xc196kx单片机及其应用系统设计[M].北京:清华大学出版社,2002:173-213. |
| [12] | 谢晗,吴光强,邱绪云.基于xPC目标的实时仿真技术及实现[J].微计算机信息,2006(22):200-202.XIE Han,Wu Guangqiang,QIU Xuyu.Realtime simulation and realization based on xPC target[J].Microcomputer Information,2006(22):200-202. |
| [13] | 李升波,王建强,李克强.硬件在环仿真试验台监控系统的设计与开发[J].系统仿真学报,2007,19(16):3684-3687.LI Shengbo,WANG Jianqiang,LI Keqiang.Development of real-time monitor system for hardware-in-the-loop simulator[J].Journal of System Simulation,2007,19(16):3684-3687. |
| [14] | 杨正贤,孔宪仁,王继河,等.基于xPC的小卫星半物理仿真验证平台[J].系统仿真学报,2009,21(20):6444-6448.YANG Zhengxian,KONG Xianren,WANG Jihe,et al.Hardware-in-loop simulation platform for small based on xPC real-time simulator[J].Satellite Journal of System Simulation,2009,21(20):6444-6448. |
| [15] | 蒋疆,罗宏.气制动ABS调节器性能参数测试系统研究与设计[J].测控技术,2012,31(8):110-113.JIANG Jiang,LUO Hong.Research and design of test system for the performance parameter of pneumatic braking ABS regulator[J].Measurement&Control Technology,2012,31(8):110-113. |
| [16] | 宋彦龙.基于xPC电机台架的综合数据采集系统[D].长春:吉林大学,2014:9-10.SONG Yanlong.Integrated data acquisition system based on xPC Motor Jack Horse[D].Changchun:Jilin University,2014:9-10. |



