2. 解放军电子工程学院 通信对抗工程系, 安徽 合肥230037
2. Department of Communication Countermeasure Engineering, Electronic Engineering Institute, Hefei 230037, China
数字信号调制模式识别能够在未知调制信息或有干扰的条件下,正确识别出通信信号调制的模式,并进一步为解调器选择相应的解调算法提供依据。调制模式识别在军事和民用中有着重要的研究前景和应用价值。在军事领域[1],数字通信信号调制模式识别是敌对双方进行通信侦察和干扰的前提,一旦明确了敌方通信系统的调制模式,就可以解调出敌方信号,获得有用的情报信息,从而为制定侦察与反侦察、干扰与反干扰策略提供有力依据,最终实现通信对抗;在民用领域[2],政府有关部门可以利用调制模式识别进行信号确认、干扰识别和频谱监测等无线电管理工作,以防止用户对无线频谱的非法利用和干扰,保证合法通信的正常进行。
调制模式识别一般采用统计模式识别方法和决策论方法。目前应用较多的为统计模式识别方法[3]。基于统计模式识别的方法可以分成2个部分:特征提取和分类器设计,其中好的特征是决定分类正确率的关键因素。现有的特征提取方法有基于时频分析的方法[4]、基于累积量的方法[5]、基于谱相关法方法[6]等。然而以上很多通用算法都是在信噪比较高时才能对信号进行识别,在信噪比降低到10 dB以下时识别率明显下降,算法有效性会大大降低。王建新等[7]利用星座图的方法得到了识别MASK、MPSK、MQAM信号的特征参数,此方法提取的特征对噪声不敏感,在低信噪比下依然有着很高的识别率,但是识别的信号种类较少。为了满足识别要求,研究抗噪声性能好、识别信号类型多、分类性能优的调制模式自动识别方法将很有意义。
近些年来,随着分形理论研究的深入,分形方法在许多基础的信号和图像处理中取得了目前最好的效果[8]。不同信号的分形维数不同,因此分形维数中包含了一定的分类信息,可以应用于模式识别领域中。吕铁军等[9]通过对信号调制规律的研究,首次提出从信号的分形维数中提取特征参数,并在识别CW、MPSK、MFSK中取得了很好的效果。郭双冰[10]通过对调制信号进行小波变换,利用变换后的小波系数提取了2种分形特征,取得了较高的识别率。但是经典的小波分析是基于傅里叶分析的,因此具有傅里叶分析的不足:一方面只能给出线性情况的解释,另一方面表现在小波基被选定后,必须用它来分析所有数据,因此不具有自适应性。针对通信信号调制模式的特点,本文提出一种新的特征提取方法。该方法首先利用Hilbert-Huang Transform (HHT)提取数字信号的边际谱,利用分形的方法提取特征,最后利用SVM进行调制模式的分类识别。
1 HHT变换和分形原理 1.1 HHT变换1998年N.E. Huang等[11]提出了信号时频分析方法HHT,由于其具有的超自适应性,非常适用于非线性和非平稳信号的处理,因此非常适于处理具有典型非平稳性的数字调制信号。HHT理论中主要是经验模式分解(EMD)和Hilbert变换,具体实现过程如下:
不妨设待识别信号为x(t),首先通过EMD[12]方法将x(t)分解为n个内蕴模式分量IMF 和一个剩余分量之和:
| $x\left( t \right) = \sum\limits_{i = 1}^n {{c_i}\left( t \right) + {r_n}\left( t \right)} $ |
式中:ci(t)是第i个内蕴模式分量,rn(t)为剩余分量。EMD的目的是通过对非线性非平稳信号的分解获得一系列表征信号特征时间尺度的本征模态函数(IMF),使得各个IMF是窄带信号,从而可以进行Hilbert分析。通过式(1) 对每一个分量IMF 进行Hilbert变换:
| ${\hat c_i}\left( t \right) = \frac{1}{\pi }P\int\limits_{ - \infty }^\infty {\frac{{{c_i}\left( t \right)}}{{t - \tau }}} {\text{d}}\tau $ | (1) |
式中:P表示柯西主值。然后通过式(2) 和式(3) 计算每一层信号的瞬时频率ωi(t)和瞬时幅值ai(t)。
| ${a_i}\left( t \right) = \sqrt {{c^2}_i\left( t \right) + {{\hat c}^2}_i\left( t \right)} $ | (2) |
| ${\theta _i}\left( t \right) = \arctan \frac{{{{\hat c}_i}\left( t \right)}}{{{c_i}\left( t \right)}},{\omega _i}\left( t \right) = \frac{{{\text{d}}{\theta _i}\left( t \right)}}{{{\text{d}}t}}$ | (3) |
可见,由Hilbert变换得到的幅值和频率都是时间的函数,把振幅显示在频率-时间的平面上,就可以得到Hilbert幅值谱:
| $H\left( {\omega ,t} \right) = \operatorname{Re} \sum\limits_{i = 1}^n {{a_i}\left( t \right)} {{\text{e}}^{j\int {{\omega _i}\left( t \right){\text{d}}t} }}$ |
H(ω,t)精确地描述了信号的幅值随时间和频率的变化规律。将H(ω,t)对时间积分,就得到Hilbert边际谱:
| $h\left( \omega \right) = \int_0^T {H\left( {\omega ,t} \right)} {\text{d}}t$ |
式中:h(ω)表明单位频率内的幅度分布(或者能量分布),代表着整个数据段幅度概率分布的累加。

|
| 图 1 不同信号的边际谱示意图 Fig. 1 The marginal spectrums of different modulation modes |
如图 1所示,不同的调制模式具有不同的边际谱。因此可以利用分形原理提取目标信号边际谱的分形特征。
1.2 分形原理分形是一门崭新的学科,是一个研究和处理自然与工程中不规则图形的强有力的数学理论工具,为处理非线性的系统问题提供了新思路和新方法。分形维数是分形理论中的重要参数,它有多种定义和计算方法。Hausdorff维数是分形理论中一种最基本的分形维数,但Hausdorff维数难以计算,实际应用中较多采用盒维数和信息维数[13]。
设待测集合A是Rn中的一个非空子集,对于每个正数ε,令N(A,ε)表示能够覆盖A的、边长为ε的最小的盒子数目,定义集合A的上下盒维为
| $${{\bar D}_B}\left( A \right) = \overline {\mathop {\lim }\limits_{\varepsilon \to 0} } \inf {{\ln N\left( {A,\varepsilon } \right)} \over { - \ln \varepsilon }}$$ |
| ${{{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{D}}}_{B}}\left( A \right)=\underset{\varepsilon \bar{\to }0}{\mathop{\underline{\lim }}}\,\sup \frac{\ln N\left( A,\varepsilon \right)}{-\ln \varepsilon }$ |
如果上下盒维相等,则定义A的盒维为
| ${D_B}\left( A \right) = \mathop {\lim }\limits_{\varepsilon \to 0} \frac{{\lg N\left( {A,\varepsilon } \right)}}{{ - \lg \varepsilon }}$ |
实际计算中可以取一系列不同的ε值计算得到对应的N(A,ε)值,通过式(4) 做最小二乘法线性回归,得到直线的斜率为信号的盒维数:
| ${D_B}A = {\text{polyfit}}\left( {{\text{ln}}\varepsilon ,{\text{ln}}N\left( {A,\varepsilon } \right)} \right)$ | (4) |
由定义能够得出,盒维数没有反映出空间上的分布情况,只是体现了集合的尺度问题,而信息维数恰好弥补了这一点。信息维数的定义如下:
设{Aj}(j= 1,2,…,K)是集合A的一个有限ε-格形覆盖,pj的含义是A的元素落在Aj中的概率。那么就有信息熵:
| $I\left( \varepsilon \right) = - \sum\limits_{j = 1}^K {{p_j}\lg {p_j}} $ |
假设信息熵有如下关系:
| $I\left( \varepsilon \right)\sim -\text{lg}{{\varepsilon }^{{{D}_{I}}\left( A \right)}}$ |
计算时,可通过粗视化变换得到信息维数:
| ${D_I}\left( A \right) = \frac{{I\left( \lambda \right) - I\left( {2\lambda } \right)}}{{\lg 2}}$ |
式中:样本间隔λ=1/fs,fs是采样频率。
上述的盒维数和信息维数属于单分形维数。有时面对自然界中复杂的信号,仅用单分形维数是不够的,这时候就必须同时使用多个维数来描述它,才能全面地刻画其特征,因此引入多重分形[14]的概念,对分形参数进行扩展。多重分形弥补了分形理论的不足,下面对多重分形的原理进行讨论。
如果χd表示d维欧氏空间,χd的任何子集都用X来标记。使用数学迭代或者递推的方法来分割X,并将每个部分的测度μ设定为一个不变的值,如果α表示一个与划分相关联的参数,第n次划分之后X的子集用Xnα来表示,如果${X_n} = \mathop {\lim }\limits_{n \to \infty } {X_n}\left( \alpha \right)$表示的是一个分形集,由此给出一个测度空间的二元组定义表示式 (X,μ),那么就能够把(X,μ)的其中一个子集用Xn来表示。如果在上述划分方式下,能够以几个分形子集的并集来代替(X,μ)的分形子集,而且其各自都有属于自己的分维数,那么就能够把这个分形集叫做多重分形。假如把(X,μ)按照一定的尺度δ来进行分割,定义单元测度为μα,那么μα和δ之间的关系为
| ${\mu _\alpha } \sim {\delta ^\alpha }$ |
式中:α是hölder指数。对于概率测度为μα的子集Xα的任何δ-覆盖{Ui}(i∈N),也就是0<diamUi<δ (diam代表直径)有
| $g_\delta ^r\left( {{X_\alpha },{\mu _\alpha }} \right) = \inf \left\{ {\sum {{\left( {\operatorname{diam} {U_i}} \right)}^r}|{{\left\{ {{U_i}} \right\}}_{i \in N}}} \right\}$ |
则Xα,μα的Hausdorff-r维测度定义为
| $g_{\left( {{X_\alpha },{\mu _\alpha }} \right)}^r = \mathop {\lim }\limits_{r \to 0} g_\delta ^r\left( {{X_\alpha },{\mu _\alpha }} \right)$ |
若存在临界指数f(α),使r>f(α)时,gXα,μαr=0;r<f(α)时,gXα,μαr=∞;r=f(α)时,0<gXα,μαr<∞。则称f(α)为多重分形的奇异谱。由Hausdorff维数的定义可知,f(α)就是分形子集Xα的Hausdorff维数,当$x \subset \mathop \cup \limits_{j = 1}^\infty {U_j},0 < {\text{diam}}\left( {{U_j}} \right) \leqslant \delta ,j \in N$时,
| $\eqalign{ & f\left( \alpha \right) = \inf \left\{ {r\left| {\mathop {\lim }\limits_{\delta \to 0} \inf \sum\limits_{j = 1}^\infty {{{\left( {{\text{diam}}{U_j}} \right)}^r} = 0} } \right.} \right\} = \cr & \sup \left\{ {r\left| {\mathop {\lim }\limits_{\delta \to 0} \inf \sum\limits_{j = 1}^\infty {{{\left( {{\text{diam}}{U_j}} \right)}^r} = \infty } } \right.} \right\} \cr} $ |
分析可得,当Uj是尺寸为δ的盒子时,若在[α,α+dα]范围内概率测度为μ的单元个数(即覆盖盒子数)为N(α),则$g_\delta ^r\left( {{X_\alpha },{\mu _\alpha }} \right) = N\left( \alpha \right){\delta ^r}$。因此当N(α)~δ-f(α)时,$g_{\left( {{X_\alpha },{\mu _\alpha }} \right)}^r$有限。由此可以得到
| $f\left( \alpha \right) = - \mathop {\lim }\limits_{\delta \to 0} \frac{{\ln N\left( \alpha \right)}}{{\ln \delta }}$ |
称f(α)为多重分形谱。在α~f(α)坐标系中,f(α)是一单峰图像,一个复杂的分形体,能够看到它是由一组取值不同的α值所代表的子集构成,而f(α)所反映的是这些子集的一些局部的分形特性。
如图 2所示,不同调制方式边际谱的多重分形谱的谱宽Δα=αmax-αmin不同,可以作为调制识别的特征之一。

|
| 图 2 不同调制信号边际谱的多重分形谱 Fig. 2 The multifractal spectrums of different modulation modes |
综上所述,盒维数所体现的是集合的尺度的大小,而信息维数所体现的是分形集的分布情况,多重分形的谱宽能够从局部出发来研究分形集的整体结构和特征,因此特征向量(由信息维数、分形谱以及盒维数三者构成)所体现的特征有频率、相位以及幅度的变动情况,在进行相关分类的时候以上这些特征属于有效特征集。综合上述原因,选取向量T:
| $T=\left[ {{D}_{B}}\left( A \right) {{D}_{I}}\left( A \right) \Delta \alpha \right]$ | (5) |
为了验证算法在特征提取中的有效性,首先利用MATLAB产生了7种最常用数字信号的仿真数据,这7种数字调制信号为:2ASK、4ASK、2FSK、4FSK、2PSK、4PSK、MSK,主要调制参数为:载频fc=10 kHz,采样频率fs=100 kHz,MSK码元速率fb=4×fc/5,其他信号码元速率为fb=2 000 B,频率偏移量△f =2 000 Hz。为了消除信道差异,还必须对仿真产生的数字调制信号进行功率归一化处理。
通过上述步骤产生的仿真数据在使用前,先将连续的长数据分割成便于处理的数据段,每段有2 048个采样数据,这一过程称为分帧。
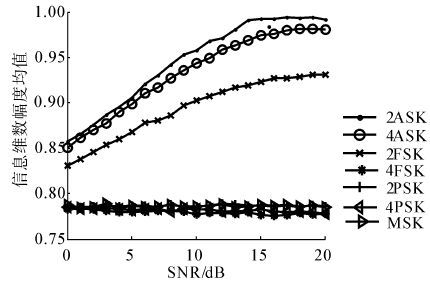
对7种调制信号加入信噪比为0~20 dB的噪声,并且以间隔1 dB变化每种信号,各提取150个特征(50个特征用于后文支持向量机的学习,100个特征用于测试分类正确率),计算特征参数的均值。计算机仿真结果如图 3~5所示:

|
| 图 3 不同调制信号边际谱盒维数均值 Fig. 3 The mean value of box dimensions |
|
| 图 4 不同调制信号边际谱信息维数均值 Fig. 4 The mean value of information dimensions |

|
| 图 5 不同调制信号边际谱多重分形谱谱宽均值 Fig. 5 The mean value of multifractal spectrum widths |
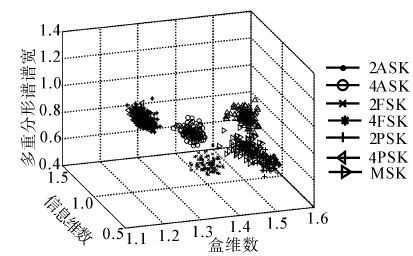
由图 3~5可得,总体上,待识别信号的特征均值向量差别较大(各参数曲线间距离较大),所以提取的分类特征能够实现信号的调制模式识别。为了更直观地说明特征包含各类调制信号的差别信息,将各信号提取的150个特征作如图 6所示的特征空间分布图。
|
| 图 6 不同调制信号特征分布图(SNR=8 dB) Fig. 6 The distribution of the features(SNR=8 dB) |
由图 6可以看出,2ASK和4ASK信号的特征混叠在一起,理论上无法加以区别,这是因为2ASK和4ASK信号的边际谱分布几乎完全相同,但是通过观察及仿真研究,由于MASK信号有相位以及振幅包络的变化,而其他调制信号的波形只有相位的变化,振幅包络是恒定的。因此直接提取数字调制信号的幅度方差:
| ${\sigma ^2} = \frac{1}{{{N_S}}}\left[ {\sum\limits_{i = 1}^{{N_S}} {a_{cn}^2\left( i \right)} } \right] - {\left[ {\frac{1}{{{N_S}}}\sum\limits_{i = 1}^{{N_S}} {{a_{cn}}\left( i \right)} } \right]^2}$ |
式中:${a_{cn}}\left( i \right) = {a_n}\left( i \right) - 1,{a_n}\left( i \right) = \frac{{\sqrt {S\left( i \right)} }}{{{m_a}}},{m_a} = \frac{1}{{{N_S}}}\sum\limits_{i = 1}^{{N_S}} {\sqrt {S\left( i \right)} } $为瞬时幅度的均值,Ns为总采样数。仿真得到150个2ASK样本的幅度方差均值为1.109 8,4ASK的幅度方差均值为1.729 7,所以设定门限TH=1.419 8,当σ2>TH判为4ASK,σ2<TH判为2ASK。得到自动识别模型如图 7所示,首先将2ASK和4ASK看成一种调制类别,利用分形特征进行分类;然后再利用特征σ2进行MASK类内识别。

|
| 图 7 调制识别模型 Fig. 7 The mode of the digital modulation recognition |
除此之外还注意到仅2PSK信号与其他信号的特征略有重叠,其余各类信号特征聚集分界线非常明显,进一步说明了本文算法的有效性。总之,以上提取的特征提供了待识别信号的差别信息,可作为本文原始特征集的元素。在提取上述特征的基础上,可以进一步进行调制模式识别。
3 识别性能分析本文使用支持向量机分类器(support vector machine,SVM)[15]测试算法的有效性。支持向量机是根据统计学习理论提出的一种机器学习方法。它不但结构简单,能够很好地解决神经网络分类器中的传统问题,而且其有着很强的鲁棒性与很好的推广性,能够很好地处理高维模式识别、小样本以及非线性等问题。SVM的本质即为求式(6) 的对偶问题:
| $\left\{ \begin{align} & \max W\left( \lambda \right)=\sum\nolimits_{i=1}^{n}{{{\lambda }_{i}}-} \\ & \sum\nolimits_{i=1}^{n}{\sum\nolimits_{j=1}^{n}{\left( {{\lambda }_{i}}{{\lambda }_{j}}{{y}_{i}}{{y}_{j}}K\left( {{x}_{i}},{{x}_{j}} \right) \right)/2}} \\ & \text{s}\text{.t}\text{.}\sum\nolimits_{j=1}^{n}{{{y}_{i}}{{\lambda }_{i}}=0} \\ & 0\le {{\lambda }_{i}}\le c \\ & i=1,2\cdots ,n \\ \end{align} \right.$ | (6) |
式中:K(xi,xj)为核函数,实现了从输入空间到高维空间的映射。由于径向基支持向量机[16]通用性较好,仿真中使用此类向量机,其核函数表达式为
| $K\left( {{x_i},x} \right) = \exp \left[ { - \sigma {{\left\| {x - {x_i}} \right\|}^2}} \right]$ | (7) |
在实际应用中,需要事先确立2个参数(惩罚因子c和式(7) 中的核参数σ),不同参数值,向量机的分类性能不同。利用粒子群算法[17]寻找最优参数的流程如下:
1) 在搜索空间中产生m个粒子,随机初始化粒子位置和初始速度;
2) 根据不同的参数σ、c,计算各粒子的适应度值,并保存各粒子的个体最优值和粒子群全局最优值;
3) 根据式(8) 计算自适应惯性权重,wmax、wmin表示w的最大值和最小值,tmax表示最大迭代步数。再根据式(9)、(10) 更新粒子的位置和速度:
| $w = {w_{\max }} - \frac{{t\left( {{w_{\max }} - {w_{\min }}} \right)}}{{{t_{\max }}}}$ | (8) |
| $v_{id}^{k + 1} = wv_{id}^k + {c_1}{r_1}\left( {p_{id}^k - x_{id}^k} \right) + {c_2}{r_2}\left( {p_{gd}^k - x_{id}^k} \right)$ | (9) |
| $x_{id}^{k + 1} = x_{id}^k + v_{id}^{k + 1}$ | (10) |
4) 迭代次数加1,判断是否满足最大迭代次数。若满足,算法终止并输出最优参数值和正确率,否则,转向2)。
最后得到最优参数值下信号的正确率如表 1。
| /% | |||||||
| 信号/dB | 2ASK | 4ASK | 2FSK | 4FSK | 2PSK | 4PSK | MSK |
| 0 | 100.00 | 99.00 | 77.00 | 84.00 | 64.00 | 91.00 | 68.00 |
| 1 | 100.00 | 100.00 | 81.00 | 88.00 | 69.00 | 95.00 | 71.00 |
| 2 | 99.00 | 99.00 | 89.00 | 91.00 | 78.50 | 92.00 | 79.00 |
| 3 | 100.00 | 99.00 | 95.00 | 93.00 | 75.00 | 98.00 | 73.00 |
| 4 | 100.00 | 100.00 | 98.00 | 96.00 | 76.00 | 99.00 | 84.00 |
| 5 | 99.00 | 100.00 | 97.00 | 94.00 | 79.00 | 99.00 | 86.00 |
| 6 | 100.00 | 99.00 | 99.00 | 98.00 | 80.00 | 100.00 | 92.00 |
| 7 | 100.00 | 100.00 | 99.00 | 99.00 | 84.00 | 99.00 | 91.00 |
| 8 | 100.00 | 100.00 | 100.00 | 97.00 | 85.00 | 99.00 | 94.00 |
| 9 | 100.00 | 100.00 | 98.00 | 99.00 | 87.00 | 100.00 | 98.00 |
| 10 | 100.00 | 100.00 | 100.00 | 100.00 | 89.00 | 100.00 | 99.00 |
| 11 | 100.00 | 100.00 | 100.00 | 99.00 | 88.00 | 100.00 | 100.00 |
| 12 | 100.00 | 100.00 | 100.00 | 99.00 | 90.00 | 100.00 | 99.00 |
| 13 | 100.00 | 99.00 | 99.00 | 100.00 | 93.00 | 100.00 | 99.00 |
| 14 | 100.00 | 100.00 | 100.00 | 100.00 | 93.00 | 100.00 | 99.00 |
| 15 | 100.00 | 100.00 | 100.00 | 99.00 | 94.00 | 99.00 | 100.00 |
| 16 | 100.00 | 100.00 | 100.00 | 100.00 | 98.00 | 100.00 | 99.00 |
| 17 | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | 99.00 | 100.00 |
| 18 | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 |
| 19 | 100.00 | 100.00 | 100.00 | 99.00 | 100.00 | 100.00 | 99.00 |
| 20 | 100.00 | 100.00 | 100.00 | 100.00 | 99.00 | 100.00 | 100.00 |
如表 1所示,计算机仿真结果表明:无需任何先验知识,在信噪比为0 ~20 dB的情况下,基于边际谱和分形理论的特征识别方法在低信噪比下就能够得到较高的调制模式识别正确率。
由表 1还可以直观地观察到,本文的方法对于高斯白噪声具有很强的抗噪性,其有效性远在传统方法之上,其原因在于通信信号的不规则程度主要取决于调制类型,而噪声对之影响较小,反映到特征上,就是分形特征对噪声不敏感,具有很强的抗噪性[9],使得最后得到的特征参数的鲁棒性得到提高。
4 结束语本文针对7种常用的数字调制信号进行了仿真,仿真结果表明:基于边际谱和分形理论提取的特征值具有更好的特征均值和方差,提高了识别的正确率,充分说明新算法有一定的有效性。但是该算法也有一定的局限性,IMF分量的边界处有些失真,这是分解中使用三次样条插值拟合时,不稳定的端点极值会出现摆动的情况,而且会在分解的过程中影响到其他的数据,进而影响了系统的识别率,这就是EMD方法中的端点效应问题。如何克服端点效应问题也是今后研究的方向之一。HHT还是一种新兴的非平稳信号处理技术,随着研究的深入,会有越来越多的学者加入到这一新兴方向的研究队伍中,新算法也层出不穷,相信以上问题以后会得到解决。
| [1] | 罗吉. 数字调制信号识别算法研究[D]. 成都: 电子科技大学, 2008: 1-2. LUO Ji. The algorithm research of digital modulation recognition[D]. Chengdu: University of Electronic Science and Technology, 2008: 1-2. |
| [2] | 刘娟. 数字通信信号自动调制识别算法研究[D]. 重庆: 重庆大学, 2009: 2-3. LIU Juan. The algorithm research of modulation recognition of digital communication signal[D]. Chongqing: Master Dissertation of Chongqing University, 2009: 2-3. |
| [3] | DOBRE O A, ABDI A, BAR-NESS Y. Blind modulation classification: a concept whose time has come[C]//IEEE Sarnoff Symphosium. Princeton, USA, 2005: 223-228. |
| [4] | HASSAN K, DAYOUB I, HAMOUDA W. Automatic modulation recognition using wavelet transform and neural network[C]//Proceedings of the 9th International Conference on Intelligent Transport Systems Telecommunications. Chicago, USA, 2009: 234-238. |
| [5] | 吕新正, 魏平, 肖先赐. 利用高阶累积量实现数字调制信号的自动识别[J]. 电子对抗技术,2004, 19 (6) : 3 –6. LV Xinzheng, WEI Ping, XIAO Xianci. Automatic identification of digital modulation signals using high order cumulants[J]. Electronic Warfare Technology,2004, 19 (6) : 3 –6. |
| [6] | 郭黎利, 齐琳, 王东凯. 软件无线电中基于谱相关理论的调制模式识别技术[J]. 哈尔滨工程大学学报,2004, 125 (6) : 799 –802. GUO Lili, QI Lin, WANG Dongkai. Modulation recognition technique using spectral correlation approach in software radio[J]. Journal of Harbin Engineering University,2004, 125 (6) : 799 –802. |
| [7] | 王建新, 宋辉. 基于星座图的数字调制方式识别[J]. 通信学报,2004, 25 (6) : 166 –173. WANG Jianxin, SONG Hui. Digital modulation recognition based on constellation diagram[J]. Journal of China Institute of Communications,2004, 25 (6) : 166 –173. |
| [8] | 林俊, 熊刚, 王智学. 基于分形特征提取的调制信号识别[J]. 弹箭与制导学报,2004, 24 (3) : 358 –363. LIN Jun, XIONG Gang, WANG Zhixue. Modulation classification based on fractal features[J]. Journal of Projectiles, Rockets, Missiles and Guidance,2004, 24 (3) : 358 –363. |
| [9] | 吕铁军, 郭双冰, 肖先赐. 调制信号的分形特征研究[J]. 中国科学: E辑,2001, 31 (6) : 508 –513. LV Tiejun, GUO Shuangbin, XIAO Xianci. Modulation signals research based on fractal features[J]. Science in China: Ser E,2001, 31 (6) : 508 –513. |
| [10] | 郭双冰. 基于小波和分形理论的调制信号特征提取方法研究[J]. 信号处理,2005, 21 (3) : 111 –115. GUO Shuangbing. A method of feature extraction for modulated signals based wavelet and fractal theory[J]. Signal Processing,2005, 21 (3) : 111 –115. |
| [11] | HUANG N E, SHEN Z, LONG S R, et al. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis[J]. Proceedings of the Royal Society: Lond A,1998, 454 : 903 –995. |
| [12] | 赵知劲, 尹霆, 郭殿武. 一种基于HHT的数字调制信号识别方法[J]. 微波学报,2006, 22 (3) : 66 –70. ZHAO Zhijin, YIN Ting, GUO Dianwu. A method to Identify digital modulation signals based on the Hilbert-Huang transform[J]. Journal of Microwaves,2006, 22 (3) : 66 –70. |
| [13] | 张旻, 钟子发, 王若冰. 通信电台个体识别技术研究[J]. 电子学报,2009, 37 (10) : 2125 –2129. ZHANG Min, ZHONG Zifa, WANG Ruobing. Research on the technique of individual communication transmitter identification[J]. Acta Electronica Sinica,2009, 37 (10) : 2125 –2129. |
| [14] | 李彤, 商朋见. 多重分形在掌纹识别中的研究[J]. 物理学报,2007, 56 (8) : 4393 –4400. LI Tong, SHANG Pengjian. A multifractal approach to palmprint recognition[J]. Acta Physica Sinica,2007, 56 (8) : 4393 –4400. |
| [15] | 何晓琴, 白勇, 冉启阳. 基于支持向量机的Freegate软件流量检测研究[J]. 计算机科学,2012, 39 (11) : 89 –90. HE Xiaoqin, BAI Yong, RAN Qiyang. Freegate software flow test research based on support vector machine[J]. Computer Science,2012, 39 (11) : 89 –90. |
| [16] | 张翔, 田金文, 肖晓玲, 等. 支持向量机及其在医学图像分类中的应用[J]. 信号处理,2004, 20 (2) : 208 –212. ZHANG Xiang, TIAN Jinwen, XIAO Xiaoling, et al. Support vector machine and its application in medical images classification[J]. Signal Processing,2004, 20 (2) : 208 –212. |
| [17] | KENNEDY J, EBERHART R C. Particle swarm optimization[C]//Proceedings of IEEE International Conference on Neural Networks. Perth, Australia, 1995: 1942-1948. |
| [18] | 易苏军. Hilbert-Huang变换及其在信号处理中的应用[D]. 大连: 大连理工大学, 2006: 9-10. YI Sujun. Hilbert-Huang transform and its application in signal processing[D]. Dalian: Dalian University of Technology, 2006: 9-10. |



