2. 广西混杂计算与集成电路设计分析重点实验室, 广西 南宁 530006
2. Guangxi Key Laboratory of Mixed Computing Integrated Circuit Design and Analysis, Nanning 530006, China
萤火虫算法(firefly algorithm,FA)是在2008年由英国剑桥学者Yang提出的一种启发式智能优化方法[1-2],其基本思想来源于萤火虫成虫利用发光的生物学特性而表现出来的觅食、求偶、警戒等社会性行为。算法提出后,受到国内外许多学者的关注和研究,并且已经成功应用于组合优化[3]、路径规划[4]、图像处理[5]、经济调度[6]等领域。与其他优化算法类似,基本FA算法的随机性较大,且存在收敛速度慢、求解精度不高的问题。为此,国内外学者对该算法进行不少的研究,刘长平[7]通过逻辑自映射函数产生混沌序列,引入到萤火虫算法中对精英个体进行混沌优化,同时动态收缩搜索空间以加快收敛速度;S.M. Farahani [8]在每一次迭代中通过高斯分布使所有萤火虫向全局最优的萤火虫移动来增加算法的收敛速度;X.S. Yang [9]在基本萤火虫算法中加入Levy飞行移动策略,增强了算法的寻优性能;A. Gandomi[10]把12种混沌映射引入到萤火虫算法中,并分析了不同的混沌映射对于标准函数优化的影响;M. Subutic[11]提出了一种求解非约束优化问题的并行萤火虫算法;A. Abdullah[12]提出了一种混合进化萤火虫算法,它把差分进化算法的进化操作融入到萤火虫算法中,改善了算法的搜索精度和萤火虫之间的信息共享;S. Farahani[13]提出了3种改进基本萤火虫的方法:1) 利用学习自动机影响吸收因子和随机化参数,2) 将遗传算法和萤火虫算法混合,3) 根据高斯分布随机移动以保证萤火虫遍布整个搜索空间;冯艳红[14]提出一种基于混沌理论的动态种群萤火虫算法,提高了算法的全局收敛能力。上述改进的算法虽然取得了一定的效果,但算法在收敛性、稳健性方面还有改进的空间。
本文从提高个体的多样性角度出发,通过在萤火虫算法中引入单纯形法的反射、扩张、压缩操作对较差位置的萤火虫作改进,提高个体的多样性,避免其陷入局部最优,以提高算法的求解精度。通过对标准测试函数以及非线性方程组的实验仿真,并与其他算法进行的对比分析表明了文中提出的基于单纯形法的萤火虫算法具有较强的跳出局部极值能力和较高的计算精度。
1 单纯形法的萤火虫算法 1.1 基本萤火虫算法在自然界中,大约存在2 000多种萤火虫,大多数种类都会发出其独特的荧光,目前对萤火虫发光的真实目的还不清楚,一般认为萤火虫利用闪光信号来吸引异性或者是吸引潜在的猎物,实现求偶或觅食的目的。萤火虫算法就是模拟这种发光的生物学特性而表现出来的社会性行为而设计的随机优化算法。在萤火虫算法中存在2个关键的要素:自身亮度和吸引度。自身亮度反映了萤火虫位置的优劣,亮度小的萤火虫会被亮度大的吸引,并向亮度大的萤火虫方向移动,吸引度影响着萤火虫所要移动的距离,通过萤火虫的移动,每个个体自身亮度和吸引度得到不断更新,最终实现目标优化的目的[2]。
在萤火虫算法中[1],萤火虫吸引度的大小和亮度的大小是成正比的,亮度由目标函数决定。一个萤火虫在坐标为X的位置,它的亮度I可以取I(X)=f(X),X的位置越好,它的亮度就越大,它对其他个体的吸引度随着它们之间距离的增加而变小,另外在荧光传输的过程中,会被传播介质吸收一部分,所以吸引度的大小还和介质吸收因子有关。因此,一个萤火虫对距离其r处的亮度I称为相对亮度。
| $I\left( r \right) = {I_0}{e^{ - \gamma {r_{ij}}}}$ | (1) |
式中:I0是萤火虫对距离其r=0处的荧光亮度,γ是介质吸收因子,rij是萤火虫i到萤火虫j的欧式距离。萤火虫的吸引度β被定义为
| $\beta = {\beta _{min}} + ({\beta _0} - {\beta _{min}}){e^{ - \gamma {r^2}}}$ | (2) |
式中:β0为萤火虫对距离r=0处的吸引度,βmin为最小吸引度,βmin=0.2。萤火虫i被萤火虫j吸引的移动公式为
| ${x_i} = {x_i} + \beta ({x_j} - {x_i}) + \alpha (\operatorname{rand} - 1/2)$ | (3) |
式中:xi、xj分别表示萤火虫i和j的位置,α为步长因子,rand表示[0,1]上服从均匀分布的随机因子。为使算法效果更好,在式中用αSk来代替α,其中Sk表示空间规模参数,并使α随着迭代次数的增加逐渐的减小,其更新公式为
| $\alpha = \alpha {({10^ \wedge }\left( { - 4} \right)/{\alpha _0})^ \wedge }(1/N{\text{Gen}})$ |
式中:α0选0.9,NGen表示最大迭代次数。
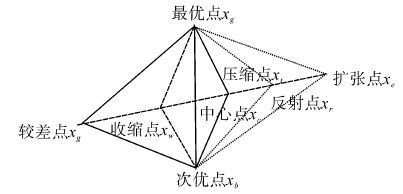
1.2 单纯形法策略为提高萤火虫算法的搜索性能,本文引入传统的单纯形法策略[15-16],在一次迭代完成之后,利用单纯形法搜索策略,选择K个位置较差的萤火虫进行优化。单纯形法是指在一个空间中构造一个多面体,求出多面体各个顶点的适应值并作比较,找出最优点、次优点以及最差点,通过反射、压缩、扩张等操作更新最差点,形成一个新的多面体。它是一种局域的搜索方法,具有简单易用、适用范围广、收敛速度快的特点。假设较差萤火虫的位置为xs,xc为最优位置和次优位置的中心。
反射操作:xr=xc+δ(xc-xs),xr为反射点,反射系数δ通常取1。
扩张操作:xt=xc+φ(xs-xc),xe为扩张点,扩张系数φ通常取2。
压缩操作:xt=xc+φ(xs-xc),xt为压缩点,压缩系数φ通常取0.5。
收缩操作:xw=xc-φ(xs-xc),xw为收缩点,收缩系数与压缩系数相同。
单纯形法的步骤如下:
1) 计算所有搜索点的目标函数值,找到最优点xg,次优点xb,对应的目标函数分别记为f(xg)、f(xb),计算它们的中心位置:xc=(xg+xb)/2。
2) 找出若干个较差萤火虫的位置,取其中一个记为xs,目标函数值记为f(xs)。将xs执行反射操作,得到反射点xr。
3) 如果f(xr)>f(xg),说明反射方向正确,执行扩张操作得到扩张点xe,如果f(xe)>f(xg),则用xe取代xs,否则,用xr取代xs。
4) 如果f(xr)<f(xs),说明反射方向更差,执行压缩操作得到压缩点xt,如果f(xt)>f(xs),则用xt取代xs。
5) 如果f(xs)<f(xr)<f(xg),执行收缩操作得到收缩点xw,如果f(xw)>f(xs),则用xw取代xs,否则,用xr取代xs。
|
| 图 1 单纯形法搜索 Fig. 1 The searching of simplex method |
从上面的分析可以看出,萤火虫算法和其他的算法一样存在步长因子α和吸引度β的确定不易性问题,定得小了,局部搜索的精度提高,但要实现整体区域的搜索所需的时间必定会长;而若定得大了,则搜索精度不高。因此,在萤火虫算法的搜索过程中,通过其他方式增加算法的局部的搜索机制是一个改进算法性能的思考方向。为此,拟结合以单纯形法的局部性能改进萤火虫算法性能。通过在算法过程中,以适当的方式增加单纯形法的局部搜素,提高萤火虫算法的局部性能。
1.4 基于单纯形法的萤火虫算法流程1) 初始化算法的参数,萤火虫数目m,步长因子α0,最大吸引度β0,最小吸引度βmin,介质吸收因子γ,最大迭代次数Tmax;
2) 随机初始化m个萤火虫的位置Xi(i=1,2,...,m),计算各自的目标值作为自己的最大亮度I0;
3) 根据式(1)、(2) 计算各个萤火虫之间的相对亮度I和吸引度β,依照I的大小确定萤火虫的移动方向;
4) 利用式(3) 对萤火虫的位置进行更新,随机扰动处在最好位置的萤火虫;
5) 根据上述单纯形法的步骤来更新较差萤火虫的位置,重新计算更新后萤火虫的亮度;
6) 判断是否满足结束条件,若是,转到7),否则转3),进入下一次搜索;
7) 输出最优位置和最优解。
2 仿真实验本文对14个标准测试函数和2个非线性方程组进行仿真测试来证明SMFA算法的性能。实验仿真在MATLAB 2012a上实现。参数设置:SMFA中,种群规模为N=20,每次用单纯形策略优化的萤火虫个数取K=10,步长因子α0=0.9,最大吸引度β0=1,最小吸引度βmin=0.2,介质吸收因子γ=1,最大迭代次数为200。PSO算法中设置的种群大小为400,GA算法利用的是GATOOL工具箱,设置的交概率为0.95,变异概率为0.05,种群规模为1 000。
2.1 标准函数测试对每个函数独立运行20次,表 1列出了标准测试函数的搜索空间、维数以及最优值等参数;表 2列出了20次实验得到的最好值、最差值、平均值以及标准差,并与GA、FA、PSO进行比较。为了直观地反映出算法的寻优效果,给出了函数的收敛曲线图,如图 2~15。
| 函数 | 取值范围 | 维数 | 最优值 |
| ${f_1}\left( x \right) = \sum\limits_{i = 1}^N {x_i^2} $ | [-100,100] | 30 | 0 |
| ${f_2}\left( x \right) = \max \left\{ {\left| {{x_i}} \right|} \right\}$ | [-10,10] | 30 | 0 |
| ${f_3}\left( x \right) = \sum\limits_{i = 1}^N {\left| {{x_i}} \right|} + \prod\limits_{i = 1}^N {\left| {{x_i}} \right|} $ | [-5,5] | 30 | 0 |
| ${f_4}\left( x \right) = \sum\limits_{i = 1}^N {i \cdot x_i^4} $ | [-100 100] | 30 | 0 |
| ${f_5}\left( x \right) = \frac{1}{{4000}}\sum\limits_{i = 1}^N {x_i^2} - \prod\limits_{i = 1}^N {\cos \left( {\frac{{{x_i}}}{{\sqrt i }}} \right)} + 1$ | [-100,100] | 30 | 0 |
| ${f_6}\left( x \right) = {\sum\limits_{i = 1}^N {\left( {\sum\limits_{j = 1}^i {{x_j}} } \right)} ^2}$ | [-100,100] | 30 | 0 |
| ${f_7}\left( x \right) = \sum\limits_{i = 1}^N {\left( {x_i^2 - 10\cos \left( {2\pi {x_i}} \right) + 10} \right)} $ | [-5.12,5.12] | 30 | 0 |
| ${f_8}\left( x \right) = - 20\exp \left( { - 0.2\sqrt {\frac{1}{N}\sum\limits_{i = 1}^N {x_i^2} } } \right) - \exp \left( {\frac{1}{N}\sum\limits_{i = 1}^N {\cos \left( {2\pi {x_i}} \right)} } \right) + 20 + e$ | [-32,32] | 30 | 0 |
| ${f_9}\left( x \right) = 0.5 + \frac{{{{\sin }^2}\sqrt {{x^2} + {y^2}} - 0.5}}{{{{\left( {1.0 + 0.001\left( {{x^2} + {y^2}} \right)} \right)}^2}}}$ | [-10,10] | 2 | 0 |
| ${f_{10}}\left( x \right) = 4x_1^2 - 21x_1^4 + x_1^6/3 + {x_1}{x_2} - 4x_2^2 + 4x_2^4$ | [-5,5] | 2 | -1.031 628 5 |
| ${f_{11}}\left( x \right) = {\sum\limits_{i = 1}^N {x_i^2 + \left( {0.5 \cdot \sum\limits_{i = 1}^N {i \cdot {x_i}} } \right)} ^2} + {\left( {0.5 \cdot \sum\limits_{i = 1}^N {i \cdot {x_i}} } \right)^4}$ | [-10,10] | 30 | 0 |
| ${f_{12}}\left( x \right) = \left( {\sum\limits_{i = 1}^N {{{\sin }^2}{x_i} - \exp \left( { - \sum\limits_{i = 1}^N {x_i^2} } \right)} } \right) \cdot \exp \left( { - \sum\limits_{i = 1}^N {{{\sin }^2}\sqrt {\left| {{x_i}} \right|} } } \right)$ | [-10,10] | 30 | 0 |
| ${f_{13}}\left( x \right) = \left[ {\sum\limits_{i = 1}^N {i \cdot \cos \left( {i + \left( {i + 1} \right)x} \right)} } \right] \cdot \left[ {\sum\limits_{i = 1}^N {i \cdot \cos \left( {i + \left( {i + 1} \right)y} \right)} } \right]$ | [-10,10] | 30 | -186.730 9 |
| $\eqalign{ & {f_{14}}\left( x \right) = \sum\limits_{i = 1}^N {\left( {\sum\limits_{k = 0}^{20} {\left[ {{{0.5}^k}\cos \left( {2\pi \cdot {3^k} \cdot \left( {{x_i} + 0.5} \right)} \right)} \right]} } \right)} - \cr & N\left( {\sum\limits_{k = 0}^{20} {{{0.5}^k}\cos \left( {2\pi \cdot {3^k} \cdot 0.5} \right)} } \right) \cr} $ | [-0.5,0.5] | 30 | 0 |
| 函数 | 算法 | 最好值 | 最差值 | 平均值 | 标准差 |
| f1(x) | GA | 0.417 | 3.0012 | 1.6196 | 0.6893 |
| PSO | 0.000022044 | 0.0045326 | 0.00090107 | 0.0012 | |
| FA | 0.0021 | 0.0198 | 0.0094 | 0.0047 | |
| SMFA | 0.000060822 | 0.00012023 | 0.000078623 | 0.0000154 | |
| f2(x) | GA | 0.2842 | 0.5066 | 0.3781 | 0.0577 |
| PSO | 0.3414 | 0.9075 | 0.5231 | 0.1368 | |
| FA | 0.0325 | 0.123 | 0.0734 | 0.0259 | |
| SMFA | 0.0003597 | 0.00069269 | 0.00048727 | 0.000091948 | |
| f3(x) | GA | 0.2797 | 0.4677 | 0.3537 | 0.0553 |
| PSO | 0.2323 | 1.1647 | 0.5779 | 0.27 | |
| FA | 0.1275 | 0.615 | 0.2594 | 0.0986 | |
| SMFA | 0.0011 | 0.0017 | 0.0014 | 0.0001366 | |
| f4(x) | GA | 0.4471 | 28.3755 | 5.1217 | 6.9575 |
| PSO | 0.000000034428 | 0.00056015 | 0.000050477 | 0.00012746 | |
| FA | 0.0000043494 | 0.0012 | 0.00032584 | 0.00034666 | |
| SMFA | 0.0000000026442 | 0.0000000186 | 0.0000000088315 | 0.0000000041325 | |
| f5(x) | GA | 0.0405 | 0.1097 | 0.0798 | 0.0159 |
| PSO | 0.00012338 | 0.035 | 0.0134 | 0.0113 | |
| FA | 0.0111 | 0.0598 | 0.035 | 0.0156 | |
| SMFA | 0.000027321 | 0.0198 | 0.0033 | 0.0062 | |
| f6(x) | GA | 680 | 10064 | 4180 | 2529 |
| PSO | 0.0094 | 20.1921 | 1.7123 | 4.6576 | |
| FA | 0.0051 | 1.0781 | 0.2872 | 0.3135 | |
| SMFA | 0.00000040511 | 0.0000062227 | 0.0000016454 | 0.0000013051 | |
| f7(x) | GA | 0.7892 | 2.4461 | 1.6428 | 0.4602 |
| PSO | 21.8891 | 94.5208 | 52.5337 | 16.1777 | |
| FA | 6.3146 | 50.789 | 21.9832 | 10.1794 | |
| SMFA | 9.9496 | 28.8538 | 19.4515 | 5.9037 | |
| f8(x) | GA | 0.391 | 0.9019 | 0.648 | 0.1329 |
| PSO | 2.3168 | 5.7346 | 3.9434 | 0.8761 | |
| FA | 0.0391 | 0.1608 | 0.0949 | 0.0294 | |
| SMFA | 0.0023 | 0.0035 | 0.0028 | 0.00040266 | |
| f9(x) | GA | 0.000010985 | 0.0097215 | 0.0058796 | 0.0048221 |
| PSO | 0 | 0 | 0 | 0 | |
| FA | 0.00040376 | 0.0099 | 0.0092 | 0.0021 | |
| SMFA | 0.000000000156 | 0.0097 | 0.0058 | 0.004 | |
| f10(x) | GA | -1.03162813513 | -1.03109911215 | -1.03154263511 | 0.00011698 |
| PSO | -1.03162845348 | -1.03162845348 | -1.03162845348 | 4.5562E-16 | |
| FA | -1.03162845318 | -1.02993337108 | -1.03154368824 | 0.00037902 | |
| SMFA | -1.03162845344 | -1.03162844885 | -1.03162845231 | 0.0000000012234 | |
| f11(x) | GA | 12.3142 | 76.8738 | 37.7178 | 19.2428 |
| PSO | 0.0019 | 0.4049 | 0.095 | 0.0964 | |
| FA | 8.7363 | 118.488 | 50.7591 | 25.8198 | |
| SMFA | 0.0000020357 | 0.000011976 | 0.0000052737 | 0.0000029126 | |
| f12(x) | GA | 2.3516E-15 | 7.5467E-15 | 4.1634E-15 | 1.3202E-15 |
| PSO | 5.6712E-17 | 0.000000000000017706 | 4.2222E-15 | 4.4641E-15 | |
| FA | 0.000000000000030442 | 0.00000000000028097 | 0.00000000000013763 | 0.000000000000071422 | |
| SMFA | 9.2235E-19 | 1.9669E-18 | 1.407E-18 | 2.8271E-19 | |
| f13(x) | GA | 0.13271736 | 0.13537165 | -186.698521 | 0.059177908 |
| PSO | -186.730908 | -186.730908 | -186.730908 | 5.83201172E-14 | |
| FA | -186.730908 | -123.576767 | -180.547112 | 15.1037764 | |
| SMFA | -186.730908 | -186.730892 | -186.730906 | 0.00000350027904 | |
| f14(x) | GA | 0.7479 | 1.2731 | 1.0328 | 0.1377 |
| PSO | 12.2142 | 17.3382 | 14.7436 | 1.4191 | |
| FA | 4.2064 | 7.1498 | 5.4376 | 0.8514 | |
| SMFA | 0.0436 | 1.0517 | 0.3388 | 0.3852 |
|
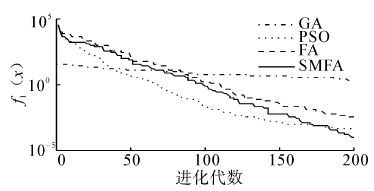
| 图 2 函数f1(x)的收敛曲线图 Fig. 2 Convergence curve of function 1 |
|
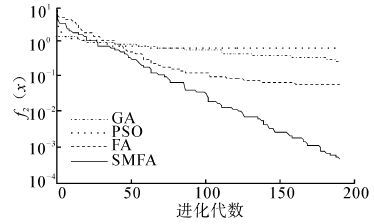
| 图 3 函数f2(x)的收敛曲线图 Fig. 3 Convergence curve of function 2 |
|
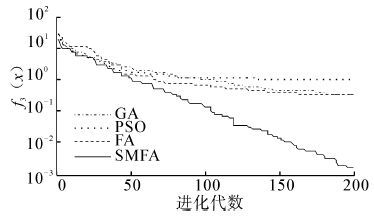
| 图 4 函数f3(x)的收敛曲线图 Fig. 4 Convergence curve of function 3 |
|
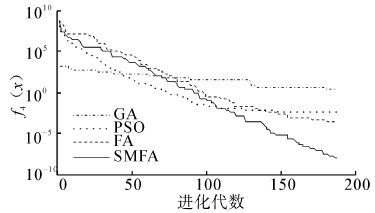
| 图 5 函数f4(x)的收敛曲线图 Fig. 5 Convergence curve of function 4 |
|
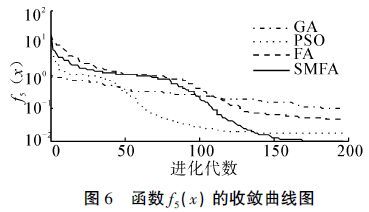
| 图 6 函数f5(x)的收敛曲线图 Fig. 6 Convergence curve of function 5 |
|
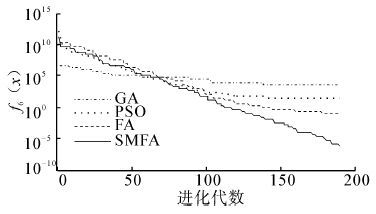
| 图 7 函数f6(x)的收敛曲线图 Fig. 7 Convergence curve of function 6 |
|
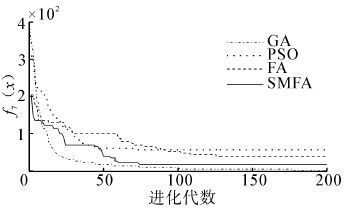
| 图 8 函数f7(x)的收敛曲线图 Fig. 8 Convergence curve of function 7 |
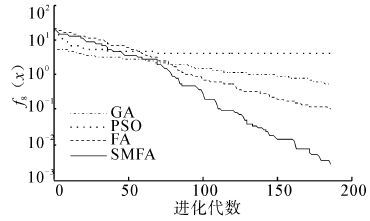
|
| 图 9 函数f8(x)的收敛曲线图 Fig. 9 Convergence curve of function 8 |
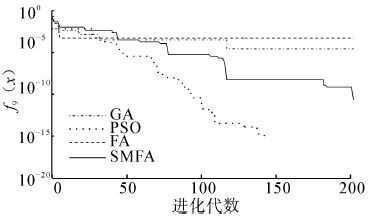
|
| 图 10 函数f9(x)的收敛曲线图 Fig. 10 Convergence curve of function 9 |
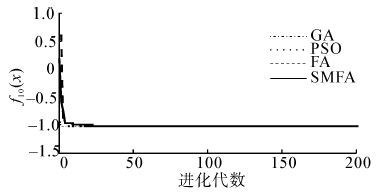
|
| 图 11 函数f10(x)的收敛曲线图 Fig. 11 Convergence curve of function 10 |
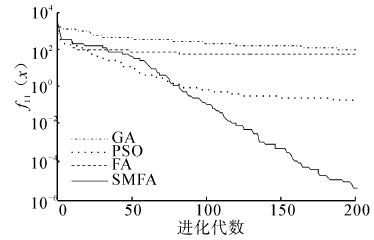
|
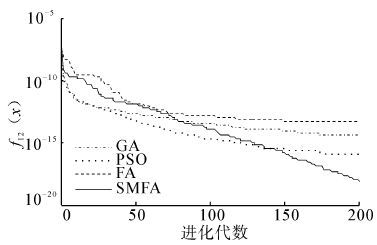
| 图 12 函数f11(x)的收敛曲线图 Fig. 12 Convergence curve of function 11 |
|
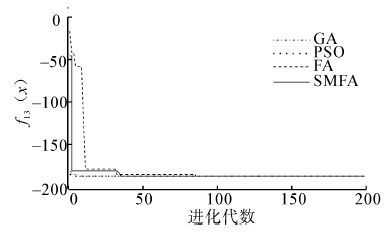
| 图 13 函数f12(x)的收敛曲线图 Fig. 13 Convergence curve of function 12 |
|
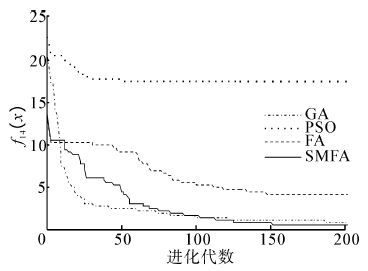
| 图 14 函数f13(x)的收敛曲线图 Fig. 14 Convergence curve of function 13 |
|
| 图 15 函数f14(x)的收敛曲线图 Fig. 15 Convergence curve of function 14 |
从表 2中的结果可以看出,SMFA与GA、PSO、FA相比,SMFA有更好的搜索最优值能力,所得到的结果更加接近标准值。对于单峰函数f1,SMFA的求解精度比FA提高2个数量级。对于函数f2,SMFA的求解精度最高,比GA、PSO高了3个数量级,比FA提高了2个数量级。对于单峰函数f3,SMFA的求解精度最高,平均求解精度比GA、PSO、FA都提高了2个数量级。对于函数f4,GA没能找到理想值,SMFA的求解精度最高,比FA提高了5个数量级,比PSO提高了4个数量级。对于多峰函数f5,SMFA的最优值求解精度达到e-5,平均的求解精度比GA、PSO、FA都提高了一个数量级。对于函数f6,SMFA的最优值求解精度达到e-7,平均求解精度比FA提高了5个数量级,GA和PSO在最大迭代次数内没有找到最优解。对于多峰函数f7,GA的求解效果最好,FA、SMFA、PSO都不能得到理想最优解,相比较而言,SMFA比FA、PSO求解效果要好。对于多峰函数f8,SMFA的求解精度最高,平均求解精度比FA提高一个数量级,比GA提高2个数量级,比PSO提高3个数量级。对于多峰函数f9,它是一个二维函数,PSO求解的最优值为0,其求解精度明显高于SMFA、FA和GA,SMFA、FA和GA的求解精度相同。对于函数f10,SMFA的标准差比FA的标准差提高了5个数量级,说明了SMFA有着更强的鲁棒性和稳定性。对于函数f11,GA和FA无法在迭代次数内找出最优解,SMFA的求解精度达到e-6,比PSO提高4个数量级。对于函数f12,SMFA的求解精度最高,最优值求解精度达到e-19,平均求解精度比FA提高5个数量级,比GA、PSO提高4个数量级。对于函数f13,SMFA的性能明显优于FA,标准差远远高于FA,说明SMFA更稳定。对于函数f14,PSO没有找到理想值,SMFA的最优值求解精度比FA高出2个数量级。从上面的数据也可以看出,SMFA在高维空间的搜索能力比PSO更强。从图 2~15可以直观地看出,SMFA能够跳出局部最优,使得求解的精度更高,它的搜索性能要强于其他算法。
2.2 非线性方程组测试方程组1[15]
| $\left\{ \begin{align} & f\left( x \right)=\exp \left( {{x}_{1}} \right)+{{x}_{1}}{{x}_{2}}-1=0 \\ & f\left( x \right)=\sin \left( {{x}_{1}}{{x}_{2}} \right)+{{x}_{1}}+{{x}_{2}}-1=0 \\ \end{align} \right.$ |
| 算法 | 方程组的解 | 方程组的值 |
| Effati算法 | (0.009 6,0.997 6) | (-0.019 223,0.016 776) |
| 进化算法 | (-0.001 38,1.002 7) | (-0.002 76,-6.37e-05) |
| FA | (-0.000 001 660 189 777,1.000 019 088 722 269) | (-3.320 409 866 724 994e-06,1.576 831 102 423 348e-05) |
| SMFA | (-0.000 000 121 372 643,1.000 002 607 766 152) | (-2.427 455 950 693 158e-07,2.365 020 549 399 688e-06) |
方程组2[47]
| $\left\{ \begin{align} & f\left( x \right)=\cos \left( 2{{x}_{1}} \right)-\cos \left( 2{{x}_{2}} \right)-0.4=0 \\ & f\left( x \right)=2\left( {{x}_{2}}-{{x}_{1}} \right)+\sin \left( 2{{x}_{2}} \right)-\sin \left( 2{{x}_{1}} \right)-1.2=0 \\ \end{align} \right.$ |
| 算法 | 方程组的解 | 方程组的值 |
| 牛顿法 | (0.15,0.49) | (-0.001 68,0.014 97) |
| Effati算法 | (0.157 5,0.497 0) | (-0.005 455,0.007 93) |
| 进化算法 | (0.157 772,0.494 58) | (0.001 264,0.000 969) |
| FA | (0.156 492 455 873 759,0.493 348 303 841 159) | (-2.982 796 363 260 043e-05,2.067 354 706 003 499e-05) |
| SMFA | (0.156 517 641 480 708,0.493 373 274 655 021) | (-3.676 025 453 591 691e-06,-1.405 665 974 729 686e-07) |
从表格3和表格4的结果可以看出,FA和SMFA相比较牛顿法、Effati算法、进化算法来说,求出的结果更接近理论最优值。SMFA比FA有更高的求解精度。
3 结束语本文针对基本萤火虫算法存在易陷入局部最优、求解精度低的不足,提出了一种基于单纯形法的萤火虫算法(SMFA)。算法中通过单纯形搜索策略对较差位置的萤火虫作改进,有效地避免了算法陷入局部最优。通过对标准函数和非线性方程组的仿真实验,证明了SMFA算法的有效性和可行性,在跳出局部最优能力、求解精度以及鲁棒性方面都要优于基本的FA算法。关于算法的收敛性证明以及算法的应用是进一步要做的工作。
| [1] | YANG X S. Nature-inspired metaheuristic algorithms. : Luniver Press[M]. 2008 : 1 -30. |
| [2] | YANG X S. Firefly algorithms for multimodal optimization[C]//Stochastic Algorithms: Foundations and Applications. Sapporo, Japan, 2009, 5792: 169-178. |
| [3] | SAYADI M K, RAMEZANIAN R, GHAFFARI-NASAB N. A discrete firefly meta-heuristic with local search for make span minimization in permutation flow shop scheduling problems[J]. International Journal of Industrial Engineering Computations,2010, 1 (1) : 1 –10. |
| [4] | BANDA M, SRIVASTAVA P R, YANG X S, et al. Optimal test sequence generation using firefly algorithm[J]. Swarm and Evolutionary Computation,2013, 8 : 44 –53. |
| [5] | HORNG M H, LIOU R J. Multilevel minimum cross entropy threshold selection based on the firefly algorithm[J]. Expert Systems with Applications,2011, 38 : 14805 –14811. |
| [6] | 郭丽萍, 李向涛, 谷文祥. 改进的萤火虫算法求解阻塞流水线调度问题[J]. 智能系统学报,2013, 8 (1) : 33 –38. GUO Liping, LI Xiangtao, GU Wenxiang. An improved firefly algorithm for the blocking flow shop scheduling problem[J]. CAAI Transactions on Intelligent Systems,2013, 8 (1) : 33 –38. |
| [7] | 刘长平, 叶春明. 具有混沌搜索策略的萤火虫优化算法[J]. 系统管理学报,2013, 22 (4) : 538 –543. LIU Changping, YE Chunming. Firefle algorithm with chaotic search strategy[J]. Journal of Systems & Management,2013, 22 (4) : 538 –543. |
| [8] | FARAHAN S M, ABSHOURI A, NASIRI B, et al. A Gaussian firefly algorithm[J]. International Journal of Machine Learning and Computing,2011, 1 (5) : 448 –454. |
| [9] | YANG X S. Firefly algorithm, levy flights and global optimization[C]//Research and Development in Intelligent SystemsXXVI. Berlin, Germany, 2010: 209-218. |
| [10] | GANDOMI A, YANG X S, TALATAHARI S, et al. Firefly algorithm with chaos[J]. Communications in Nonlinear Science and Numerical Simulation,2013, 18 (1) : 89 –98. |
| [11] | SUBUTIC M, TUBA M, STANAREVIC N. Parallelization of the firefly algorithm for unconstrained optimization problems[J]. Latest Advances in Information Science and Applications,2012, 22 (3) : 264 –269. |
| [12] | ABDULLAH A, DERIS S, MOHAMAD M, et al. A new hybrid firefly algorithm for complex and nonlinear problem[J]. Distributed Computing and Artificial Intelligence,2012, 14 (4) : 673 –680. |
| [13] | FARAHANI S, ABSHOURI A, NASIRI B, et al. Some hybrid models to improve firefly algorithm performance[J]. International Journal of Artificial Intelligence,2012, 8 (12) : 97 –117. |
| [14] | 冯艳红, 刘建芹, 贺毅朝. 基于混沌理论的动态种群萤火虫算法[J]. 计算机应用,2013, 33 (3) : 796 –805. FENG Yanhong, LIU Janqin, HE Yichao. Chaos-based dynamic population firefly algorithm[J]. Journal of Computer Applications,2013, 33 (3) : 796 –805. |
| [15] | 张红霞, 罗毅, 师瑞峰. 基于单纯形法的改进型人工鱼群算法[J]. 计算机应用,2011, 31 (5) : 1321 –1327. ZHANG Hongxia, LUO Yi, SHI Ruifeng. Artificial fish swarm algorithm based on simplex method[J]. Journal of Computer Applications,2011, 31 (5) : 1321 –1327. |
| [16] | 曲良东, 何登旭, 黄勇. 自适应改进和声—单纯形进化算法研究[J]. 计算机应用研究,2013, 30 (3) : 676 –678. QU Liangdong, HE Dengxu, HUANG Yong. Research on adaptive improved harmony—simplex evolutionary algorithm[J]. Application Research of Computers,2013, 30 (3) : 676 –678. |
| [17] | GROSAN C, ABRAHAM A. A new approach for solving nonlinear equations systems[J]. IEEE Trans Systems and Humans,2008, 38 (3) : 698 –714. |



