社会系统本质上是一个复杂系统,特别是随着现代社会的飞速发展,对资源的需求也越来越大。单项资源已无法支撑整个社会的全面发展,且只有各单项资源互相耦合、互相牵制,才能形成强大的支撑合力。一旦某种或几种资源缺失或失效,社会系统的内在结构及功能会遭到极大的破坏。例如,2003年9月28日发生在意大利的大面积停电事件,最初由于一个供电站的失效致使众多供电站与整个供电网的脱离,随后又致使众多Internet网络节点失效,最终致使整个电力调度系统无法调控,导致了更大规模的停电[1-2]。
随着通信网、电力网、交通网、供水网等复杂动态网络的发展,以及大型高速计算机、巨型数据库以及GPS和基于大数据的社会计算的普及,复杂动态网络特别是多节点不规则连接的有向网络的牵制控制越来越受到关注。如刘彧[3]研究了复杂动态网络节点从任意初态控制到任意终态的完全能控性问题;王文旭[4]提出了一种减少控制节点的方法;Nepusz[5]研究了运用点边互换的思想对网络的边的状态进行控制的问题;严钢[6]研究了控制复杂网络的能量代价问题。
1 网络模型 1.1 模型示例一个复杂动态网络是具有相互耦合和牵制关系的点或网络所组成的网络系统。一般用被线连接起来的点来代表网络。这些点被称为节点,是网络的参与者;线则被称为链路,代表参与者之间的联系。
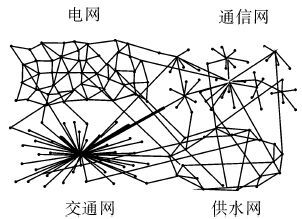
如图 1所示,电网互相传输电力,通信网之间互相传输数据,交通网之间互相运输,供水网之间互相供水,同时电网进行电力传输需要通信网进行控制,通信网之间互相通讯又依赖于电网的供电等。如果这些网络中的一个节点受到攻击而失效,这些牵制关系能使故障在网络之间传播。如图 2所示,一个节点受到攻击后,最初有12个运行节点的网络最后只剩下4个有效节点。
|
| 图 1 网络示例 Fig. 1 A network example |

|
| 图 2 失效的传播 Fig. 2 A propagation of the failure |
近年来,许多实证研究证明,社会系统中的许多网络,都满足幂律分布[7-9],即少数主导节点具有非常大的连接数,大多数节点的连接数甚小,以互联网为例,如图 3所示。

|
| 图 3 全球排名前1 000网站 Fig. 3 The 1 000 most-visited sites on the web |
图 3勾勒了全球排名前1 000的网站,这个网络一共有1 000个网站和2万条有向链接,全球的网站分成了两大阵营。左边这一块的核心是google、youtube、facebook等,右边的核心是百度、优酷、人人网等。
如图 4所示,这1 000个网站度分布是个长尾分布,但有一个明显的截断。这是因为只考虑了排名靠前的网站,这个排名范围以外的网站数据是极度不全的。从分布来看,是一个类幂律分布,斜率大概是0.8,而Barabasi等[2]估计的互联网链接幂律分布指数是2.1。这有2种原因:1) 近年来互联网变得更不平等;2) 只监测了重大流量的链接结构,相当于互联网里的rich club,也就是说网络中的链接是更不平等的。
基于这些实证,牵制控制[11]的本质通过复杂网络中的少数节点影响网络中的其他节点,从而实现整个网络的同步,所需解决的问题包括:
1) 可行性问题:当网络规模很大时,控制理论中已有的判据和算法的计算复杂度往往难以承受,因此需要寻找新的有效算法;
2) 经济性问题:选取受控节点代价的最小化;
3) 鲁棒性问题:大规模复杂网络往往面临由于随机故障或者有意攻击而导致的节点或链路失效。因此,有必要研究控制系统对于随机故障和有意攻击的鲁棒性。特别地,需要能够给出判别大规模网络控制系统中的关键节点和链路的有效算法;
4) 演化性问题:很多实际网络的结构和参数往往是随时间演化的,这给系统的有效分析与控制带来新问题,需要有适合演化网络的判断依据与有效算法。
面对这些问题,很重要的一点就是对网络进行牵制[12],使得其网络的最终状态满足一定要求。但对于大规模的网络,不可能控制其每个节点,仅能对网络中的少数关键节点进行控制,通过节点间的相互耦合,从而达到控制整个网络的目的。
1.2 复杂网络的牵制模型[13]给定时间t和状态空间中的一点x(t),复杂网络动态变化过程可表示为
| $\dot x\left( t \right) = f\left( {t,x\left( t \right),u\left( t \right)} \right),x\left( t \right) \in {R^N}$ | (1) |
考虑一个由N个节点构成的连续动力系统,其中第i个状态节点的线性耦合常微分方程[14]如式(2) 所示。
| $\eqalign{ {{\dot x}_i}\left( t \right) = f\left( {{x_i}\left( t \right),t} \right) & + c\sum\limits_{j = 1,j \ne i}^N {{G_{ij}}\Gamma \left( {{x_j}\left( t \right) - {x_i}\left( t \right)} \right)} \cr i = 1,2, \cdots ,N \cr} $ | (2) |
式中:N>1为网络节点个数;${x_i}\left( t \right) = {\left[ {{x_{i1}}\left( t \right){x_{i2}}\left( t \right) \ldots {x_{in}}\left( t \right)} \right]^T} \in {R^n}$表示i节点的状态向量;常数c>0表示耦合强度;Γ∈Rn×n表示外部耦合矩阵,由于f的线形性,Γ为正定;G=(Gij)N×N表示网络的拓扑结构,其中若存在节点j到节点i(i≠j)的连接,则Gij>0,若存在节点i到节点j(j≠i)的连接,则Gji>0,否则Gij=0。G对角元素定义为式(3)。
| ${G_{ii}} = - \sum\limits_{j = 1,j \ne i}^N {{G_{ij}}} $ | (3) |
从而满足了耗散耦合条件,如式(4) 所示。
| $\sum\limits_{j = 1}^N {{G_{ij}}} = 0$ | (4) |
此时,式(2) 可简化为
| ${\dot x_i}\left( t \right) = f\left( {{x_i}\left( t \right),t} \right) + c\sum\limits_{j = 1}^N {{G_{ij}}\Gamma {x_j}\left( t \right)} ,i = 1,2, \ldots ,N$ |
设不动点s是系统的解,如式(5) 所示。
| $\dot s = f\left( {s,t} \right),s\left( {{t_0}} \right) = {s_0}$ | (5) |
式中:s(t)可以是一个平衡点、周期轨、拟周期轨、混沌轨道,或者是多agent动态网络的虚拟领袖。假设在网络中仅前面l个节点(q1,q2,…,ql)为驱动节点,网络能被描述为式(6)、(7)。
| $\eqalign{ & {{\dot x}_i}\left( t \right) = f\left( {{x_{qi}}\left( t \right),t} \right) + c\sum\limits_{j = 1}^N {{G_{qi,j}}\Gamma {x_j}\left( t \right)} + {u_{qi}} \cr & i = 1,2, \cdots ,l \cr} $ | (6) |
| $\eqalign{ & {{\dot x}_i}\left( t \right) = f\left( {{x_{qi}}\left( t \right),t} \right) + c\sum\limits_{j = 1}^N {{G_{qi,j}}\Gamma {x_j}\left( t \right)} \cr & i = l + 1,l + 2, \cdots ,N \cr} $ | (7) |
式中:$l = \left\lfloor {\delta N} \right\rfloor ,0 < \delta < 1$,其中dqi>0为反馈控制增益,uqi是n维线性反馈控制器。
牵制控制的目标是发现一些合适的uqi以使网络能够达到某个同步状态,其中同步可表示为式(8)。
| $\mathop {\lim }\limits_{t \to \infty } \left\| {{x_i}\left( t \right) - s\left( t \right)} \right\| = 0,i = 1,2, \cdots ,N$ | (8) |
根据式(4)~(7),误差向量如式(9)。
| ${e_i}\left( t \right) = {x_i}\left( t \right) - s\left( t \right),i = 1,2, \cdots ,N$ | (9) |
当i=1,2,…,l,如式(10)、(11) 所示。
| $\eqalign{ & {{\dot e}_i}\left( t \right) = f\left( {{x_i}\left( t \right),t} \right) - f\left( {s\left( t \right),t} \right) + \cr & c\sum\limits_{j = 1}^N {{G_{ij}}\Gamma {e_j}\left( t \right) - c{d_i}\Gamma {e_i}\left( t \right)} \cr} $ | (10) |
| $\eqalign{ & {{\dot e}_i}\left( t \right) = f\left( {{x_i}\left( t \right),t} \right) - f\left( {s\left( t \right),t} \right) + c\sum\limits_{j = 1}^N {{G_{ij}}\Gamma {e_j}\left( t \right)} \cr & i = l + 1,l + 2, \cdots ,N \cr} $ | (11) |
为了获得式(10)、(11) 的收敛条件,选择Lyapunov 函数为
| $V\left( t \right) = \frac{1}{2}\sum\limits_{i = 1}^N {e_i^T{\xi _i}{e_i}\left( t \right)} $ |
设存在K使得(x-y)T(f(x,t)-f(y,t))≤(x-y)TKΓ(x-y)∀x,y∈Rn [15]成立,即满足Lipschitz 条件。根据式(8) 求导得
| $\eqalign{ & \dot V = \sum\limits_{i = 1}^N {e_i^{\text{T}}\left( t \right){\xi _i}} {{\dot e}_i}\left( t \right) = \cr & \sum\limits_{i = 1}^N {e_i^T\left( t \right){\xi _i}} \left[ {f\left( {{x_i}\left( t \right),t} \right) - f\left( {s\left( t \right),t} \right) + c\sum\limits_{j = 1}^N {{G_{ij}}\Gamma {e_j}\left( t \right)} } \right] - \cr & c\sum\limits_{i = 1}^l {{d_i}{\xi _i}e_{_i}^{\text{T}}\left( t \right)\Gamma {e_i}\left( t \right)} \leqslant \cr & \sum\limits_{i = 1}^N {e_i^{\text{T}}\left( t \right){\xi _i}} \left[ {K\Gamma {e_i}\left( t \right) + c\sum\limits_{j = 1}^N {{G_{ij}}\Gamma {e_j}\left( t \right)} } \right] - \cr & c\sum\limits_{i = 1}^l {{d_i}{\xi _i}e_{_i}^{\text{T}}\left( t \right)\Gamma {e_i}\left( t \right)} = \cr & {e^{\text{T}}}\left( t \right)\left[ {\Xi \otimes \left( {KT} \right) + c\left( {\hat G - \Xi D} \right) \otimes \Gamma } \right]e\left( t \right) \cr} $ | (12) |
式中:
| $\begin{align} & e\left( t \right)=\left[ e_{1}^{\text{T}}\left( t \right)e_{2}^{\text{T}}\left( t \right)\cdots e_{N}^{\text{T}}\left( t \right) \right] \\ & \Xi =\text{diag}\left( {{\xi }_{1}},{{\xi }_{2}},\cdots ,{{\xi }_{N}} \right) \\ & D=\text{diag}\left( {{d}_{1}},\cdots {{d}_{l}},0,\cdots ,0 \right) \\ \end{align}$ |
当D=0,表明来自外部的入度很高,无需控制便能达到同步,⊗ 为kronecker积,
| $G = \left( {\Xi G + {G^{\text{T}}}\Xi } \right)/2$ |
设θ=λmax(K+KT)/2 ,由于θ与K的可互换性得:
| $\eqalign{ & {\left( {x - y} \right)^{\text{T}}}\left( {f\left( {x,t} \right) - f\left( {y,t} \right)} \right) \leqslant \cr & \theta {\left( {x - y} \right)^{\text{T}}}\Gamma \left( {x - y} \right)\forall x,y \in {R^n} \cr} $ |
若V≤0,误差逐渐趋向于零,则网络同步,可得式(16)。
| $C = \theta \Xi + c\left( {\hat G - \Xi D} \right) < 0$ | (13) |
式中:${C_{ij}} = c\frac{{{\xi _i}{G_{ij}} + {\xi _j}{G_{ji}}}}{2},\left( {i \ne j} \right)$
${C_{ij}} = \theta {\xi _i} - e{\xi _i}k_l^{in} - c{\xi _i}{d_i},\left( {1 \leqslant i \leqslant l} \right)$
${C_{ij}} = \theta {\xi _i} - e{\xi _i}k_l^{in},\left( {l + 1 \leqslant i \leqslant N} \right)$
根据式(13) 可得
| ${d_i} > \frac{\theta }{c} - k_i^{in},1 \leqslant i \leqslant l$ | (14) |
| $k_i^{in} > \frac{\theta }{c},l + 1 \leqslant i \leqslant N$ | (15) |
| $c > \frac{{{\lambda _{\max }}\left( {\theta \Xi } \right)}}{{\left| {{\lambda _{\max }}\left( {G - \Xi D} \right)} \right|}}$ | (16) |
随着移动技术与社会化媒体的迅速发展,人们越来越多地参与到网络上丰富的社会活动中。人们在享受前所未有的便捷的同时,也拥有了网络这一公共话语平台,但同时个性会自觉的消失而群体的共性便随之显现出来,形成所谓的“网民群体”。网民群体常常表现为非常烦躁、多变和冲动,将选择、判断和处理的权利交给群体领袖。群体领袖对事件的倾向性解读,在暗示和相互传染的推波助澜下,立刻会被网民接受。
给合式(6)~(8),将群体领袖作为生成树的根节点,可得式(17)。
| $\eqalign{ & {{\dot y}_i}\left( t \right) = f\left( {{y_i}\left( t \right),t} \right) + c\sum\limits_{j = 1}^N {{{\tilde G}_{ij}}\Gamma {y_j}\left( t \right)} \cr & i = 1,l + 1,2, \cdots ,N + 1 \cr} $ | (17) |
式中:${y_1} = s,{y_{i + 1}} = {x_i},\tilde G = \left[ {\begin{array}{*{20}{c}} 0&0\\ d&{G - D} \end{array}} \right]$。 由于虚拟领袖不受其他人的影响,因此${\tilde G_1} = 0$,其他节点为${\tilde G_J} = {A_j} + {B_j}$,其中Aj为行和向量为零的矩阵,Bj≤0为对角矩阵。由于式(4),存在向量${\tilde \pi _j} = {\text{diag}}\left( {{\pi _{j1}},{\pi _{j2}}, \cdots ,{\pi _{j{p_j}}}} \right)$使得$\mathop \pi \limits_j^T {A_j} = 0$。
类似式(12) 的推导,网络同步的条件为
| $\theta {\tilde \pi _j} + c\left( {{{\bar A}_j} - {{\tilde \pi }_j}{C_j}{{\bar D}_j}} \right) < 0,j = 2,3, \cdots ,m$ |
式中:${\bar A_j} = \frac{1}{2}\left( {{{\tilde \pi }_j}{A_j} + A_j^{\text{T}}{{\tilde \pi }_j}} \right),{\bar D_j} = {\text{diag}}\left( {\tilde d{,_{{r_{j - 1}} + 1}}, \cdots ,{{\tilde d}_{{r_j}}}} \right),{C_j} = {\text{diag}}\left( {{C_{{j_1}}}, \cdots ,{C_{j{p_j}}}} \right)$
1.3 算法及系统运行界面牵制控制算法具体步骤如下:
1) 系统初始化,设j=2,转到2);
2) 根据式(17) 计算${\bar D_j}$,如果${\bar D_j}$=0,则网络无需控制便可同步,转到6),否则转到3);
3) 如果节点来自外部的入度为零,比如Cj=0,根据式(17),节点必须通过${\bar D_j}$进行控制,转到4),否则转到6);
4) 对于通过j链路连接的i节点,根据式(15),如果入度$k_{{r_{j - 1}} + i}^{in} \leqslant \theta /c$,则节点必须被控制,转到5),否则转到6)
5) 筛选根节点,转到6)
6) 如果j<m,则j=j+1,转到2),否则终止。
系统运行界面如图 5所示。

|
| 图 5 运行界面 Fig. 5 Running interface |
包含10个节点的网络拓扑如图 5所示,可分解为5个部分,其中s为群体领袖,实心圆点为被驱动节点,用于牵制其余部分,空心圆点通过节点间的耦合连接关系被间接地控制。
设$f\left( {{x}_{i}},t \right)=\left\{ \begin{align} & 35\left( {{x}_{{{i}_{2}}}}-{{x}_{{{i}_{1}}}} \right) \\ & -7{{x}_{{{i}_{1}}}}-{{x}_{{{i}_{1}}}}{{x}_{i3}}+28{{x}_{{{i}_{2}}}}\Gamma =\text{diag}\left( 1,2,1 \right),c=12,N=10,\theta =31 \\ & {{x}_{{{i}_{1}}}}{{x}_{{{i}_{2}}}}-3{{x}_{{{i}_{3}}}} \\ \end{align} \right.$。子网2和3子网的外部入度均为0,必须加以控制。
对于子网2,C2=A2-=0 ,根据式(17) 如果${d_1} > \frac{\theta }{c} \approx 2.5833$,子网2能同步;
对于子网3,${C_3} = 0,{\tilde \pi _3} = {\text{diag}}\left( {8,1,3,4} \right)$
| ${\bar A_3} = \left[ {\begin{array}{*{20}{c}} { - 24}&3&9&{12}\\ 3&{ - 6}&3&0\\ 9&3&{ - 24}&{12}\\ {12}&0&{12}&{ - 24} \end{array}} \right]$ |
根据式(17)
| $\left[ {\begin{array}{*{20}{c}} { - 24 + 8\frac{\theta }{c}}&3&9&{12}\\ 3&{ - 6 + \frac{\theta }{c}}&3&0\\ 9&3&{ - 24 + 3\frac{\theta }{c}}&{12}\\ {12}&0&{12}&{ - 24 + 4\frac{\theta }{c}} \end{array}} \right] - {\tilde \pi _3}{\bar D_3} < 0$ |
由于$\left[ {\begin{array}{*{20}{c}} { - 6 + \frac{\theta }{c}}&3&0\\ 3&{ - 24 + 3\frac{\theta }{c}}&{12}\\ 0&{12}&{ - 24 + 4\frac{{\bar \theta }}{c}} \end{array}} \right] < 0$,如果d2<18.266 7,控制子网3中的节点2,子网3能同步;
对于子网4,${\tilde \pi _4} = {I_2},{C_4} = {\rm{diag}}\left( {3,4} \right),{\bar D_4} = 0$,根据式(17),无需控制便能达到同步;
对于子网5,${C_5} = {\rm{diag}}\left( {2,0,3} \right),{\tilde \pi _5} = {\rm{diag}}\left( {2,3,3} \right),{\bar A_5} = \left[ {\begin{array}{*{20}{c}} { - 6}&3&3\\ 3&{ - 6}&3\\ 3&3&{ - 6} \end{array}} \right]$根据式(15)、(17),$k_9^{in} = 2 < \frac{\theta }{c}\left[ {\begin{array}{*{20}{c}} { - 10 + 2\frac{\theta }{c}}&3&3\\ 3&{ - 6 + 3\frac{\theta }{c}}&3\\ 3&3&{ - 15 + 3\frac{\theta }{c}} \end{array}} \right] - {\bar \pi _3}{\bar D_3} < 0$,已知$ - 6 + 3\frac{\theta }{c} > 0$由于$\left[ {\begin{array}{*{20}{c}} { - 10 + 2\frac{\theta }{c}}&3\\ 3&{ - 15 + 3\frac{\theta }{c}} \end{array}} \right] < 0$,可知如果d9>2.665,控制子网5中的节点9,子网5能同步。
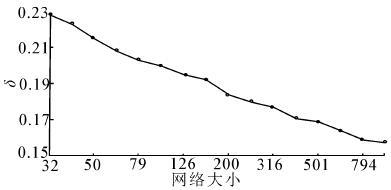
综上所述,实心节点1,2,9的d1>2.583 3,d2>18.266 7,d9>2.665 ,图中的网络可同步。如图 6所示,随着网络规模的扩大,驱动节点的比例减小,即越是稀疏的网络需要越多比例的驱动节点才能实现完全能控。
|
| 图 6 驱动节点比例与网络规模N的关系 Fig. 6 Relation between δ and N |
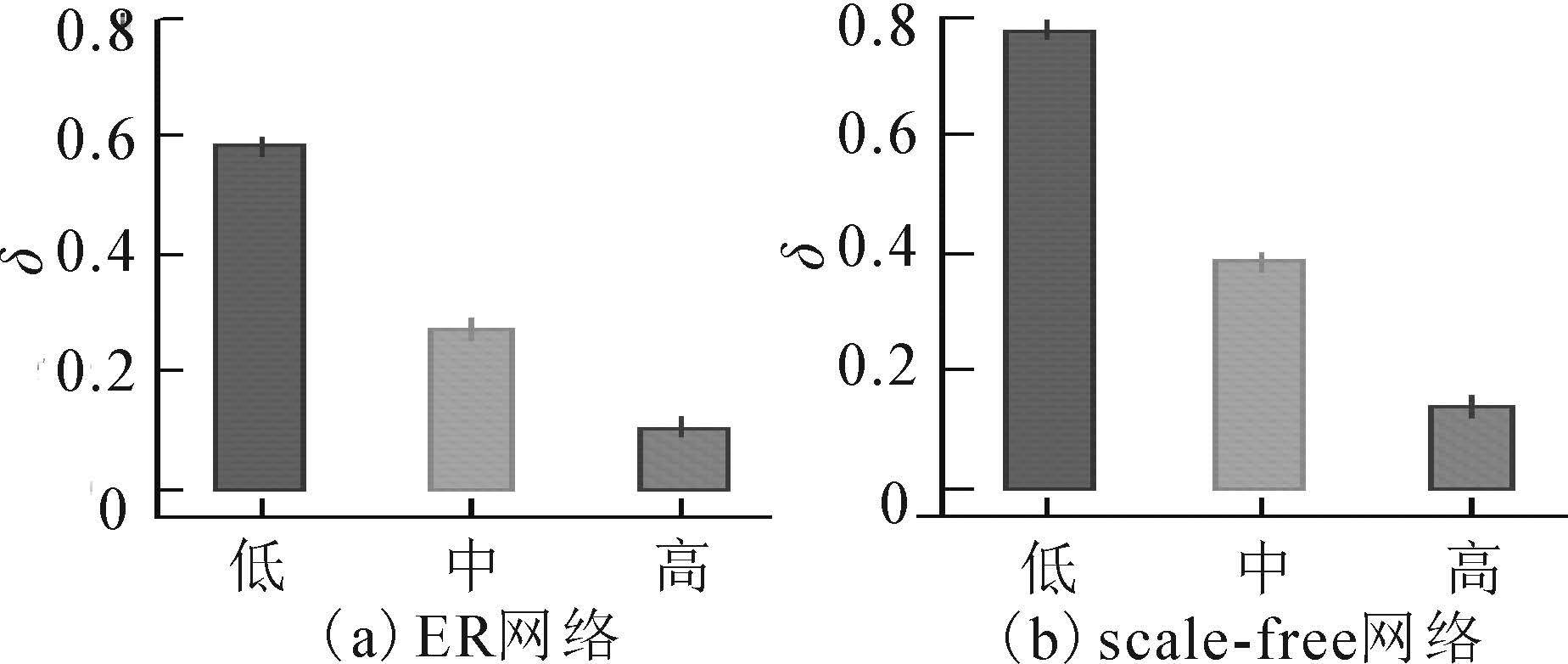
如图 7所示,分别以ER网络和Scale-free网络为例,驱动节点常常都是入度低的节点,这与式(14)、(15) 一致,也与现实情况一致,即入度低的网络控制起来比较困难,入度高的网络可通过驱动少数节点来加以控制。
|
| 图 7 驱动节点比例与其入度的关系 Fig. 7 Relation between δ and in-degree |
本文针对一般复杂网络和包含生成树的复杂网络的优化牵制控制,给出了此2种情况下复杂网络同步的条件,最后通过系统仿真,发现越是稀疏的网络需要越多比例的驱动节点才能实现完全能控,且入度低的节点应首先加以控制。
| [1] | WATTS D J, STROGATZ S H. Collective dynamics of small-world networks[J]. Nature,1998, 393 (6684) : 440 –442. |
| [2] | BARABASI A L, ALBERT R. Emergence of scaling in random networks[J]. Science,1999, 286 (5439) : 509 –512. |
| [3] | LIU Y Y, SLOTINE J J, BARABáS A L. Controllability of complex networks[J]. Nature,2011, 473 : 167 –173. |
| [4] | WANG W X, NI X, LAI Y C. Optimizing controllability of complex networks by minimum structural perturbations[J]. Phys Rev E,2012, 85 (026115) : 1 –5. |
| [5] | NEPUSZ T, VICSEK T. Controlling edge dynamics in complex networks[J]. Nature Physics,2012 (8) : 568 –573. |
| [6] | YAN G, REN J, LAI Y C. Controlling complex networks: how much energy is needed?[J]. Phys Rev Lett,2012, 108 (218703) : 1 –9. |
| [7] | NEWMAN M E J. Networks: an introduction. Oxford: Oxford University Press[M]. 2010 : 1 -20. |
| [8] | CHEN G R, WANG X F, LI X. Introduction to complex networks: models, structures and dynamics. Beijing: High Education Press[M]. 2012 : 1 -10. |
| [9] | ZHOU T, WANG B H. Catastrophes in scale-free networks[J]. Chin Phys Lett,2005, 22 : 1072 –1075. |
| [10] | Google. The 1000 most-visited sites on the web[EB/OL]. USA:Google(2011-07-19)[2012-10-25].http://www.google.com/adplanner/static/top1000. |
| [11] | RAJAPAKSE I, GROUDINE M, MESBAHI M. Dynamics and control of state-dependent networks for probing genomic organization[J]. PNAS,2011, 108 : 257 –262. |
| [12] | 汪小帆, 李翔, 陈关荣. 网络科学导论. 北京: 高等教育出版社[M]. 2012 : 1 -15. WANG Xiaofan, LI Xiang, CHEN Guanrong. Introduction of network science. Beijing: Higher Education Press[M]. 2012 : 1 -15. |
| [13] | CHEN G R, WANG X F, LI X. Introduction to complex networks: models, structures and dynamics. Beijing: High Education Press[M]. 2012 : 167 -256. |
| [14] | YU W, CAO J, LIU J. Global synchronization of linearly hybrid coupled networks with time-varying delay[J]. SIAM J Appl Dyn Syst,2008 (7) : 108 –133. |
| [15] | 柳亭, 楮衍东, 张建刚, 等. 复杂动态网络的牵制同步控制[J]. 燕山大学学报,2010, 34 (5) : 459 –470. LIU Ting, CHU Yandong, ZHANG Jiangang, et al. Pinning controlled synchronization of a complex dynamical network[J]. Journal of Yanshan University,2010, 34 (5) : 459 –470. |




