尺度不变特征变换[1](scale invariant feature transform,SIFT)作为一种稳定性好、鲁棒性强的局部特征点提取算法,在目标识别、三维重建、图像拼接、运动分析等领域得到广泛的应用[2]。然而,由于SIFT算法的时间复杂度较高,制约了该算法在实时性较高场合的应用。近年来,针对SIFT算法时间成本较高的问题,提出了一些改进方法。Bay等[3]提出的SURF(speeded up robust features)算法,Yan等[4-5]提出的PCA-SIFT算法,都在特征点检测和描述方面进行了改进。而SIFT特征点的匹配实质上是高维空间中特征向量的最近邻搜索问题。并且,在很多情况下,搜索某个特征向量的最近邻并不是必须的[6],只要得到它的近似最近邻就可以了。基于此,目前常用于SIFT特征点匹配近似最近邻搜索算法有最优节点优先算法[7](best bin first,BBF)、局部敏感哈希[8-9](locality sensitive hashing,LSH)以及近似最近邻搜索快速算法库[10-11](fast library for approximate nearest neighbors,FLANN)等。
本文在大量SIFT特征点快速匹配算法的研究基础上,基于参考向量夹角和点距离,提出了一种自适应搜索范围的近似最近邻搜索算法—AutoARV & DP(auto angle of reference vector & distance of point)用于SIFT特征点匹配。与BBF算法的对比实验表明,使用AutoARV & DP算法进行SIFT特征点匹配能够获得满意的匹配效果,同时有效地降低了SIFT特征点匹配的时间成本。
1 问题描述使用SIFT作用图像I1(x,y),检测出m个特征点,各特征点对应的特征向量构成向量集合:
| ${F_1} = \left\{ {{V_i}\left| {{V_i} = \left[ {V_i^1V_i^2 \ldots V_i^{128}} \right],i = 1,2, \ldots ,m} \right.} \right\}$ |
各特征向量对应128维空间中的点构成点集合:
| $F_{1}^{'}=\left\{ {{p}_{i}}\left| {{p}_{i}}=\left[ p_{i}^{1}p_{i}^{2}\ldots p_{i}^{128} \right],i=1,2,\ldots ,m \right. \right\}$ |
使用SIFT作用图像I2(x,y),检测出n个特征点,各特征点对应的特征向量构成向量集合:
| ${F_2} = \left\{ {{V_j}\left| {{V_j} = \left[ {V_j^1V_j^2 \ldots V_j^{128}} \right],j = 1,2, \ldots ,m} \right.} \right\}$ |
各特征向量对应128维空间中的点构成点集合:
| $F_{2}^{'}=\left\{ {{p}_{j}}\left| {{p}_{j}}=\left[ p_{j}^{1}p_{j}^{2}\ldots p_{j}^{128} \right],j=1,2,\ldots ,m \right. \right\}$ |
若在图像I1(x,y)与图像I2(x,y)之间进行特征点匹配,即是对Vx∈F1(或者Px∈F1′),从集合F2(或者F2′)中搜索与Vx(或者Px)的最近邻的向量Vx_nearest(或者Px_nearest)。其中,近邻度一般用欧式空间距离来度量。
2 自适应搜索范围的快速匹配算法—AutoARV & DP 2.1 AutoARV & DP算法基本原理对于任一查询向量Vq∈F1,需要在集合F2中搜索Vq的最近邻Vq_nearest。引入一个参考向量Vr∈R128,对于Vi∈F2,i=1,2,…,n,计算其与Vr的夹角并排序保存。求出Vq与参考向量Vr之间的夹角θ,然后在向量集合F2″中搜索,就可能得到Vq的真正最近邻[12]。
| $F_2^{''} = \left\{ {{V_i}\left| \begin{array}{l} {V_i} \in {F_2},\\ \left\langle {{V_{i,}}{V_r}} \right\rangle \in \left[ {\theta - \Delta \theta ,\theta + \Delta \theta } \right],\\ i = 1,2 \ldots ,k,k < n \end{array} \right.} \right\}$ |
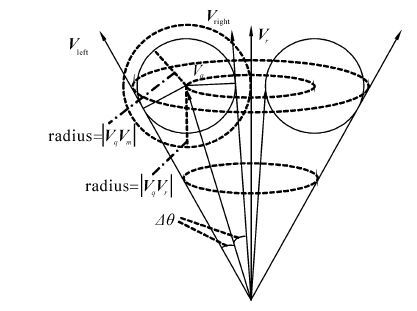
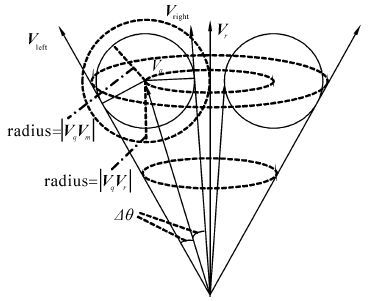
如图1所示的三维欧式空间,只需要在Vr为轴心,顶角为θ-Δθ的圆锥以外和顶角为θ+Δθ的圆锥以内的圆锥环Π空间内搜索,就可能得到向量Vq的真正最近邻。并且随着Δθ的增大,搜索到Vq_nearest的概率也随之增大。
|
| 图 1 邻域内搜索最近邻 Fig. 1 Search in the neighborhood |
由以上分析可知,选取一个合适的搜索范围Δθ是搜索到查询向量Vq最近邻的关键。Δθ太大,导致较多的无效搜索,增加了算法的时间成本,Δθ太小,可能无法找到Vq的真正最近邻。针对此,本文提出了一种自适应搜索范围的搜索方法。参考图1,若集合F2中,Vm与Vr的夹角〈Vr,Vm〉最接近Vq与Vr的夹角〈Vr,Vq〉,则Vq的真实最近邻必定落在以Vq为中心,VqVm为半径的球Ω中,据以上分析可知,若球Ω在圆锥环Π中,则必定能搜索到Vq的真实最近邻。对此,本文分2种情形分析。
1) Vm 落在以Vq为中心,|VqVr|为半径的球中 以向量Vq与Vr构成的平面α截取图1,截面图如图2所示。
|
| 图 2 情形1截面图 Fig. 2 Sectional view of situation |
由图2可知,只要保证搜索范围Δθ=$\arcsin \left( {\frac{{\left| {{V_q}{V_m}} \right|}}{{\left| {{V_q}} \right|}}} \right)$,即集合F″angle中搜索,则必定能搜索到Vq的真实最近邻。
| ${F_{angle}}'' = \left\{ \begin{array}{l} {V_i}\left| {{V_i} \in {F_2}} \right.\\ \left\langle {{V_i},{V_r}} \right\rangle \in \left[ {\theta - \Delta \theta ,\theta + \Delta \theta } \right],\\ i = 1,2 \ldots ,k,k < n \end{array} \right\}$ |
2) Vm落在以Vq为中心,|VqVr|为半径的球外, 以向量Vq与Vr构成的平面α截取图1,截面图如图3所示。

|
| 图 3 情形2截面图 Fig. 3 Sectional view of situation two |
由图3可知,此时,Δθ=arcsin$\left( {\frac{{\left| {{V_q}{V_m}} \right|}}{{\left| {{V_q}} \right|}}} \right)$,已经超过Vq与Vr之间的夹角θ,导致θ-Δθ<0。显然,由于空间的同向性,只需要取θ-Δθ=0,也即保证在集合F″angle中搜索,则一定能搜索到Vq的真实最近邻。
| ${F^{''}}_{angle} = \left\{ {{V_i}} \right.\left| \begin{array}{l} {V_i} \in {F_2},\\ \left\langle {{V_i},{V_r}} \right\rangle \in \left[ {0,\theta + \Delta \theta } \right],\\ i = 1,2, \ldots ,k,k < n \end{array} \right.$ |
经过2.2中的自适应角度筛选后,一般来讲,对于Vq∈F1,都需要对角度筛选后的向量集合F″angle中的所有向量进行比较。然而,由图1可知,Vq的真实最近邻必定落在以Vq为中心,|VqVm|为半径的球Ω中。设点Px为球Ω中的点,则有|OPx|∈[|Vq|-|VqVm|,|Vq+VqVm|],因此,为了进一步减少无效搜索,对于以上角度筛选后的向量集合F″angle,只需要考虑其中模值在上述范围中的向量即可。也即将搜索范围进一步缩小为
| ${F^{''}}_{angle + dist} = \left\{ {{V_x}} \right.\left| \begin{array}{l} {V_x} \in F_{angle}^{''},\left| {{V_x}} \right| \in \left[ \begin{array}{l} \left| {{V_q}} \right| - \left| {{V_q}{V_m}} \right|,\\ \left| {{V_q}} \right| + \left| {{V_q}{V_m}} \right| \end{array} \right]\\ x = 1,2, \ldots ,p,p < k \end{array} \right.$ |
也就是说,只需要在F″angle+dist中搜索,便可以找到Vq的真实最近邻。直观上来看,经过角度和距离筛选后的搜索空间如图4所示,为一个以Vq为中心,VqVm为半径的球在以Vr为法线且经过Vq的平面上绕Vr旋转一周形成的类似于泳圈的空间。

|
| 图 4 距离筛选后的搜索空间 Fig. 4 The search area after distance filtering |
由于对于Vq∈F1,都需要计算查询向量Vq与参考向量Vr时间的夹角〈Vq,Vr〉,并依此为依据在集合F2中搜索Vm,继而搜索Vq的最近邻。因此,参考向量Vr的选取关系到最终的匹配效果。设参考向量Vr与集合F2中所有向量之间构成的夹角构成集合
| ${Q_{angle}} = \{ < {V_r},{V_i} > {V_i} \in {F_2},i = 1,2, \cdots ,n\} $ |
显然,Qangle中的任一元素Qanglei满足Qanglei∈[0,π]。若Qangle中的元素服从[0,π]上均匀分布,即Qangle~U[0,π]。则能避免向量集中搜索增加搜索的时间成本,同时保证以较快的速度和较大的概率搜索到Vq的真实最近邻。基于此,参考向量Vr在128维空间中对应的点Pr128=(xr1,xr2,…,xr128)应该处于F2′的中心,即要求点Pr128到F2′中各点的距离和最小,即要求d最小。
| $\begin{array}{l} d = \sum\limits_{i = 1}^n {\left| {p_r^{128}{p_i}} \right|} = \\ \sum\limits_{i = 1}^n {\sqrt {{{\left( {x_r^1 - x_i^1} \right)}^2} + {{\left( {x_r^2 - x_i^2} \right)}^2} + \ldots + \left( {x_r^{128} - x_i^{128}} \right)} } \end{array}$ |
由于距离均大于零,要最小化d,即
| $\begin{array}{l} \min \left( {\sum\limits_{i = 1}^n {\left| {p_r^{128}{p_i}} \right|} } \right) = \\ \min \left( {\sum\limits_{i = 1}^n \begin{array}{l} \left( - \right)2 + \left( - \right)2\\ + \ldots + \left( {x_r^{128} - x_i^{128}} \right) \end{array} } \right) \end{array}$ |
对上式求导并令其等于零[13],则可解得
| $x_{_r}^j = \frac{1}{n}\sum\limits_{i = 1}^n {x_i^j} ,i = 1,2, \ldots ,n.j = 1,2, \ldots ,128$ |
直观上来看,即当点Pr128的各维取样本各维的均值时,其对应的向量为最佳参考向量Vr。
2.5 算法描述基于以上分析,对于Vq∈F1,在向量集合F2中搜索向量Vq的最近邻的步骤如下:
1) 根据集合F2,计算参考向量Vr。
2) 对于任一属于集合F2中向量Vi,计算其与参考向量Vr之间的夹角,保存于数组Angleri中,并建立Angleri与Vi的映射。然后对Angleri中的元素按照升序(或降序)进行排序得到Angleri_order。
3) 对于Vq∈F1,计算其与Vr之间的夹角θ。然后从Angleri_order中搜索并返回与θ最相近的元素对应的向量Vm。
4) 计算Vq与Vm之间的距离 |VqVm|以及Vq,得到Δθ=arcsin(|VqVm|/|Vq|)。
5) 在Angleri_order中,保留所有夹角在范围[θ-Δθ,θ+Δθ]中的对应向量,得到角度筛选后的向量集合Vangle。
6) 计算集合Vangle中所有向量的模,若模属于范围[|Vq|-|VqVm|,|Vq|+|VqVm|],则保留,否则剔除。得到模筛选后的向量集合Vangle+norm。
7) 使用穷举搜索法在Vangle+norm中搜索待匹配向量Vq的最近邻Vq_nearest。
步骤6) 中,若向量Vx的前i(i∈[1, 128])维的模已经大于|Vq|+|VqVm|,则无需进行后面维度的计算,直接剔除,且Vangle中所有向量的模只需计算一次。7) 中,若向量Vy与Vq的前j(j∈[1, 128])维的欧式距离已经超过上一次比较的最小距离时,直接剔除跳出,进行下一向量的比较。7) 中,为了避免可能由于集合Vangle+norm中特征向量分布过于集中而导致的过多无效搜索,本文设定一个搜索次数上限值Seektimesth
3 基于AutoARV & DP的SIFT特征点快速匹配算法本文的基本思想是首先利用SIFT算法分别提取含有同一目标的2幅图像的特征点,然后使用本文介绍的AutoARV & DP算法进行特征点的匹配。SIFT算法提取的特征点包括极大值点与极小值点2种类型[1],正确匹配的特征点之间具有相同的极值类型,基于此,在进行特征点匹配之前,首先进行特征点类型的判断,如同类型,才进行后续的匹配计算,否则直接跳出进行下一个特征点比较,这可进一步提高匹配的速度。
对于含有同一目标的2幅图像I1(x,y)和I2(x,y),本文介绍的特征点快速匹配算法具体步骤如下所述:
1) 使用SIFT算法提取图像I1(x,y)的特征点,生成的特征向量构成集合F1,提取图像I2(x,y)的特征点,生成的特征向量构成集合F2。
2) 对于Vq∈F1,基于本文描述,使用AutoARV & DP算法在F2中搜索得到Vq的最近邻特征向量Vq_nearest,对应的最近邻距离为distnearest,次近邻特征向量Vq_nearest2,对应的次近邻距离distnearest2,若$\frac{{dis{t_{nearest}}}}{{dis{t_{nearest}}_{_2}}}$小于设定的阈值ratioth,则认为Vq与Vq_nearest正确匹配[1]。
3) 使用随机抽样一致性(RANSAC)算法消除误匹配的特征点。
4 实验及结果分析为了验证本文算法的性能,本文以GitHub上Rob Hess维护的Opensift库(http://robwhess.github.io/opensift/)为基础,修改相应代码并进行实验。实验采用的测试图片部分来自Affine Covariant Features(ACF)测试图片库(http://www.robots.ox.ac.uk/~vgg/research/affine/index.html),部分来自现场拍摄。实验硬件环境:Inter(R) Core(TM)2 Duo CPU T6600,2.20GHz,2.00GB RAM。实验软件环境:Microsoft Windows7 OS,Microsoft Visual Studio 2010 IDE,Opencv2.4机器视觉库,GTK+2.24图形工具包。
为了验证AutoARV & DP算法的有效性,本文进行了AutoARV & DP算法与BBF算法在不同变化环境下的特征匹配对比实验以及两算法在不同规模特征向量集合下的匹配性能对比实验。其中,交叉验证得到两算法的最近邻与次近邻距离阈值比为0.56,且保持不变;AutoARV & DP算法中的最大搜索次数阈值Seektimesth=100;BBF算法中kdtree_bbf_knn函数的参数k=2(最近邻和次近邻),max_nn_chks=200,其他参数保持默认。
4.1 不同变化环境下的特征匹配性能对比实验本实验比较了在不同的变化环境下,AutoARV & DP算法和BBF算法的匹配性能。实验图像采用ACF测试库中的Bike(Blur),Graf(ViewPoint),Boat(Zoom+Rotation),Leuven(Light),Ubc(JPEG Compression)5组图片以及一组现场拍摄的书架图片,每组图片包含6张图片,分别使用BBF算法以及AutoARV & DP算法对每组图片中的img1和img3各进行5次匹配实验,最后使用RANSAC剔除误匹配,分别求取两算法平均每次匹配的正确匹配总数、正确匹配率以及匹配时间3个指标。实验结果如下:
| 图片 | 特征点总数 | td>BBF算法 | AutoARV & DP算法 | |||||
| Img1 | Img3 | 正确匹配总数 | 正确匹配率/% | 匹配时间/s | 正确匹配总数 | 正确匹配率 | 匹配时间/s | |
| Bike | 3 215 | 1 381 | 534 | 93.2 | 0.392 | 426 | 94.5 | 0.316 |
| Graf | 2 821 | 3 595 | 382 | 92.5 | 0.420 | 275 | 93.3 | 0.352 |
| Boat | 7 909 | 5 574 | 1 265 | 94.7 | 1.139 | 1 054 | 94.1 | 0.797 |
| Leuven | 2 218 | 1 600 | 747 | 94.2 | 0.264 | 682 | 94.8 | 0.285 |
| Ubc | 4 563 | 6 833 | 1 586 | 95.8 | 0.717 | 1 248 | 94.6 | 0.688 |
| 书架图 | 6 933 | 7 873 | 650 | 93.4 | 1.170 | 427 | 93.2 | 0.824 |
由表1可知,在正确匹配总数方面, AutoARV & DP算法稍逊于BBF算法,这可以通过适当增大Seektimesth来增加匹配总数;在正确匹配率方面,AutoARV & DP与BBF算法的表现相差无几,前者甚至更加稳定;在匹配时间方面,当特征向量集合规模较小时,AutoARV & DP算法与BBF算法相差不大,随着特征向量集合规模的增大,前者较后者有明显的优势。这是由于AutoARV & DP仅需在较小的空间中搜索有限的近似最近邻,而BBF算法基于kd-tree索引进行优先队列查询,不但受特征向量集合分布的影响,而且需要较多的回溯查询,导致时间成本较高。由此可知,本文所提出的AutoARV & DP算法能够满足不同变化环境下的特征点匹配需求,且当特征向量集合规模较大时,时间成本上由于BBF算法。
4.2 不同规模特征向量集合下的性能对比实验本实验比较了在不同规模特征向量集合下AutoARV & DP算法与BBF算法的时间成本。实验采用实验室现场拍摄图片,共2组,其中,每组20张,10张查询图像,对应10张搜索图像,特征向量集合的大小10k~40k不等。分别使用BBF算法以及AutoARV & DP算法对2组图片进行匹配实验,求取在不同特征向量集合规模N下,平均每次匹配的时间消耗。实验结果如 表2所示。
| 数据规模k | BBF算法 | AutoARV & DP算法 | |||
| 正确匹配率/% | 匹配时间/s | 正确匹配率/% | 匹配时间/s | ||
| 11.6 | 94.8 | 1.91 | 95.1 | 1.13 | |
| 13.5 | 95.2 | 2.27 | 95.0 | 1.31 | |
| 15.8 | 95.0 | 2.82 | 95.3 | 1.53 | |
| 18.3 | 94.7 | 3.19 | 94.8 | 1.74 | |
| 20.7 | 94.3 | 3.71 | 94.6 | 1.94 | |
| 24.1 | 93.8 | 4.39 | 94.5 | 2.17 | |
| 27.7 | 93.7 | 5.22 | 94.6 | 2.38 | |
| 31.2 | 93.4 | 5.92 | 94.2 | 2.54 | |
| 35.6 | 92.8 | 6.80 | 94.0 | 2.70 | |
| 38.6 | 93.0 | 7.53 | 94.3 | 2.78 | |
由表2可知,随着特征向量集合规模N的增大,BBF算法的匹配时间急剧增加,本文的AutoARV & DP算法虽然也有所增加,但其增长速率远低于BBF算法。这是由于本文的AutoARV & DP算法仅需在较小的空间中搜索有限的近似最近邻,随着数据规模的增长,需要求取更多的夹角和距离来建立待匹配样本集,但是,经过AutoARV & DP算法的夹角和距离筛选后,落在该搜索空间的样本并不会急剧增长,从而降低了时间消耗。由此可知,在特征向量集合规模较大的情况下, AutoARV & DP算法在时间成本上优于BBF算法。
5 结束语本文基于参考向量夹角和点距离,提出了一种自适应搜索范围的近似最近邻搜索算法AutoARV & DP用于SIFT特征点匹配。VGG实验室的ACF测试图片库与现场图片的测试结果表明,AutoARV & DP能够适应不同变化环境,取得较好结果的同时,降低时间成本,尤其在数据集规模较大的情况下,时间消耗明显优于经典的BBF算法。此外,若结合数据集的分布特点,搜索空间还有进一步缩小的可能,从而进一步提高算法的性能,这将是后期的研究工作重点。
| [1] | LOWE D G. Distinctive image features from scale-invariant keypoints[J]. International Journal of Computer Vision,2004, 60 (2) : 91 –110. |
| [2] | KRYSTIAN M, CORDELIA S. A performance evaluation of local descriptors[J]. IEEE Trans on Pattern Analysis and Machine Intelligence,2005, 27 (10) : 1615 –1630. |
| [3] | BAY S H, TUYTELAARS T, GOOL L V. SURF: speed up robust features[C]//Proceedings of the European Conference on Computer Vision. Graz, 2006: 404-417. |
| [4] | FARAJ A, DANIJELA R D, AXEL G. VF-SIFT: very fast sift feature matching[C]//Proc of the 32nd DAGM Symposium. Darmstadt, Germany, 2010: 222-231. |
| [5] | FARAJ A, DANIJELA R D, AXEL G. VF-SIFT: very fast sift feature matching[C]//Proc of the 32nd DAGM Symposium. Darmstadt, Germany, 2010: 222-231. |
| [6] | GIONIS A, INDYK P, MOTWANI R. Similarity search in high dimensions via hashing[C]//Proc of the 25th International Conference on Very Large Data Bases. San Francisco, USA, 1999: 518-529. |
| [7] | BEIS J S, LOWE D G. Shape indexing using approximate nearest-neighbor search in high-dimensional spaces[C]//Proceedings of the CVPR. San Juan, 1997: 1000-1006. |
| [8] | SLANEY M, CASEY M. Locality-sensitive hashing for finding nearest neighbors[J]. IEEE Signal Processing Magazine,2008, 25 (2) : 128 –131. |
| [9] | 何周灿, 王庆, 杨恒. 一种面向快速图像匹配的扩展LSH算法[J]. 四川大学学报:自然科学版,2010, 47 (2) : 269 –274. HE Zhoucan, WANG Qin, YANG Heng. An extended local sensitivity hash algorithm for efficient image matching[J]. Journal of Sichuan University: Natural Science Edition,2010, 47 (2) : 269 –274. |
| [10] | MUJA M, LOWE D G. Fast approximate nearest neighbors with automatic algorithm configuration[C]//International Conference on Computer Vision Theory and Applications. 2009: 331-340. |
| [11] | MUJA M, LOWE D G. Fast matching of binary features[C]//Conference on Computer and Robot Vision. : 2012: 404-410. |
| [12] | 吴伟交, 王敏, 等. 基于向量夹角的SIFT特征点匹配算法[J]. 模式识别与人工智能,2013, 26 (1) : 123 –127. WU Weijiao, WANG Min. SIFT feature matching algorithm based on vector angle[J]. Pattern Recognition and Artificial Intelligence(PR & AI),2013, 26 (1) : 123 –127. |
| [13] | 同济大学数学系. 高等数学. 北京: 高等教育出版社[M]. 2007 : 109 -113. |



