粒子滤波(particle filter,PF)算法是一种基于蒙特卡罗模拟和递推贝叶斯估计的滤波方法,随着采样粒子数的增大,逐渐趋向状态的后验概率密度,在处理非高斯、非线性系统的参数估计和状态滤波问题方面有着明显的优势。近年来,在目标跟踪、卫星姿态估计、金融领域数据分析、图像处理、卫星导航动态定位等方面得到广泛的应用[1-5]。对于粒子滤波而言,其主要的缺陷是存在粒子退化现象。采用重采样技术能抑制粒子退化现象,但同时也带来了粒子的多样性丧失、样本枯竭等问题。 文献[6]将卡尔曼滤波与粒子滤波结合提高估计精度。文献[7]将粒子滤波与神经网络结合,可克服神经网络算法易陷于局部极小的缺陷。文献[8]将粒子滤波与自组织模糊神经网络训练算法相结合,利用粒子滤波对参数进行学习,其在结构紧凑性和泛化性能上有所提高。上述这些算法是将粒子滤波用于神经网络算法的改善。
1 基本粒子滤波算法Gordon提出基于蒙特卡罗方法的序贯重要性重采样粒子滤波算法以来,粒子滤波成为非线性非高斯系统状态估计问题的一个研究热点[9]。
假设描述动态系统的状态方程和观测方程为
| ${{X}_{k}}={{f}_{k}}\left( {{X}_{k}}_{-1},{{v}_{k-i}} \right)Zk={{h}_{k}}\left( {{X}_{k}},{{n}_{k}} \right)$ |
式中:Xk为状态向量,Zk为测量向量,fk为状态转移函数,hk为状态向量和观测向量之间的传递函数,vk-1为系统噪声,nk为观测噪声。基本粒子滤波算法的步骤如下所示。
设k-1时刻有一组后验粒子集:
| $\left\{ {{x_{k - 1}}\left( i \right),{\omega _{k - 1}}\left( i \right);i = 1,2, \ldots ,N} \right\}$ |
式中:N为粒子数目,xk-1(i)为k-1时刻的第i个粒子,ωk-1(i)为k-1时刻第i个粒子的权重。
1) 粒子集初始化,k=0。
根据先验概率密度p(X0)抽取随机样本,X0(1),X0(2),…,X0(N)(N为随机样本数)。
2) 当k=1,2,…时,执行以下步骤:
① 状态预测。根据系统的状态方程抽取k时刻的先验粒子:
| $\left\{ {{X}_{k|k-1}}\left( i \right);i=1,2,\ldots ,N \right\}\sim p\left( {{X}_{k}}|{{X}_{k-1}} \right)$ |
② 更新。首先,进行权值更新。在获得测量值之后,根据系统的观测方程计算粒子的权值ωk(j):
| ${\omega _k}^{(j)}:{\omega _k}^{(i)} = {\omega _{k - 1}}^{(i)}p\left( {{Z_k}|{X_k}^{(i)}} \right),i = 1,2, \ldots ,N$ |
归一化权值为
| ${\tilde \omega _k}^{\left( i \right)} = {{{\omega _k}^{\left( i \right)}} \over {\sum\nolimits_{i = 1}^N {{w_k}^{\left( i \right)}} }},\sum\limits_{i = 1}^N {{{\tilde \omega }_k}^{\left( i \right)}} = 1$ |
然后,计算有效粒子数${{\hat N}_{{\rm{eff}}}}$,并与设定的阈值Nthres进行比较;如果${{\hat N}_{{\rm{eff}}}}$<Nthres,则对先验粒子集$\left( {{X_k}{|_k}{{_{ - 1}}^{\left( i \right)}},{{\tilde \omega }_k}^{\left( i \right)}} \right)$进行重采样,得到N个等权值的粒子$\left( {{X_k}{|_k}{{_{ - 1}}^{\left( i \right)}},\frac{1}{N}} \right)$。否则,执行③。
③ 估计。计算当前时刻系统的状态估计值:
| ${{\hat X}_k}{\rm{ = }}\sum\limits_{i = 1}^N {{X_k}{|_k}{{_{ - 1}}^{\left( {\rm{i}} \right)}}} {{\tilde \omega }_k}^{\left( i \right)}$ |
基本粒子滤波算法在k时刻抽样时保持了过去的样本不变,而且重要性权是迭代计算的。但重要性权的方差经过若干次迭代,某个权可能趋于1,其余的权趋于0,造成了权值退化现象。粒子滤波的重采样可以抑制权值的退化,但重采样后也带来粒子不再独立。
2 BP神经网络辅助的粒子滤波算法BP神经网络是一种有教师信号的按误差逆传播算法训练的多层前馈网络。它的学习规则使用最速下降法,通过反向传播来不断调整网络的权值和阈值,使网络的误差平方和最小。BP神经网络模型拓扑结构包括输入层、隐层和输出层,如图 1所示。
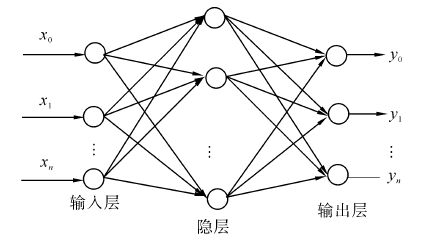
|
| 图 1 BP神经网络结构示意图 Fig. 1 Diagram of BP neural network |
设输入样本为p个:x1,x2,…,xp,与之对应的教师信号为d1,d2,...,dp,实际输出为y1,y2,…,yp,输出误差为
| $E = \frac{1}{2}\mathop \sum \limits_{k = 1}^p {\left( {{d_k} - {y_k}} \right)^2}$ |
采用梯度法对各个层之间的权值进行调整,以使总误差减小,即
| $\Delta {w_{jk}} = - |\eta \frac{{\partial E}}{{\partial {w_{jk}}}}$ |
式中:η为学习步长,wjk为各层之间的权值,Δwjk为权值修改量,通过总误差对权值进行相应地调整。
将BP神经网络与粒子滤波算法结合,改进的粒子滤波在基本粒子滤波的基础上增加了权值分裂和权值调整2个步骤,BP神经网络辅助的重要性权值调整粒子滤波(NNWA-PF)算法详细步骤如下。
1) 粒子集初始化,k=0。
根据先验概率密度p(X0)产生随机样本,X0(1),X0(2),…,X0(N)(N为随机样本数)。
2) 当k=1,2,…时,执行以下步骤:
① 状态预测。根据系统的状态方程抽取k时刻的先验粒子:
| $\left\{ {{X}_{k|k-1}}\left( i \right);i=1,2,\ldots ,N \right\}\sim p\left( {{X}_{k}}|{{X}_{k-1}} \right)$ |
② 进行权值更新。在获得测量值之后,根据系统的观测方程并计算粒子的权值ωk(j):
| ${\omega _k}^{(j)}:{\rm{ }}{\omega _k}^{(i)} = {\omega _{k - 1}}^{(i)}p\left( {{Z_k}|{X_k}^{(i)}} \right),i = 1,2, \ldots ,N$ |
归一化权值为
| ${{{\tilde{\omega }}}_{k}}^{\left( i \right)}=\frac{{{\omega }_{k}}^{\left( i \right)}}{\mathop{\sum }^{}\overset{N}{\mathop{_{i=1}}}\,{{\omega }_{k}}^{\left( i \right)}},\underset{i=1}{\overset{N}{\mathop{\mathop{\sum }^{}}}}\,{{{\tilde{\omega }}}_{k}}^{\left( i \right)}=1$ |
③ 粒子分裂。将粒子矩阵按权值大小排序,分为高权值矩阵和低权值矩阵,将高权值矩阵中q个权值大的粒子分裂为2个小的、权值减半的粒子,同时将低权值矩阵中的q个权值最小的粒子舍弃。
④ 权值调整。将③的粒子权值矩阵进行降序排列,取其中最小的q个粒子,利用BP神经网络调整粒子的权值。
设误差能量定义为
| $\varepsilon = \frac{1}{2}\mathop \sum \limits_{i = 1}^q {\left( {{z_k} - {y_k}} \right)^2}\frac{1}{2}\mathop \sum \limits_{k = 1}^q e\mathop {_k}\limits^2 $ |
式中:q为输入/输出层神经元的数量,zk为教师信号,即系统在该时刻的量测值,yk为神经网络的输出。输入数据为具有较小权值的粒子,其状态值作为BP神经网络的输入,粒子权值作为神经网络的初始权值,样本的学习函数为系统量测方程。
对更新后的粒子的权值进行归一化,
| ${{{\tilde{\omega }}}_{k}}^{\left( i \right)}=\frac{{{\omega }_{k}}^{\left( i \right)}}{\mathop{\sum }^{}\overset{N}{\mathop{_{i=1}}}\,{{\omega }_{k}}^{\left( i \right)}},\underset{i=1}{\overset{N}{\mathop{\mathop{\sum }^{}}}}\,{{{\tilde{\omega }}}_{k}}^{\left( i \right)}=1$ |
⑤ 重采样。计算有效粒子数N^eff,并与设定的有效粒子数阈值Nthresthres进行比较;如果N^eff<Nthres,则进行重采样。将原来的带权样本{x(i)0:k,w(i)k}Ni=1映射为等权样本{x(i)0:k,N-1}Ni=1。否则,执行⑥。
⑥ 估计。计算当前时刻系统的状态估计值:
| ${{{\hat{X}}}_{k}}=\underset{i=1}{\overset{N}{\mathop{\mathop{\sum }^{}}}}\,{{X}_{k|k}}{{_{-1}}^{\left( i \right)}}{{{\tilde{\omega }}}_{k}}^{\left( i \right)}$ |
⑦ 时刻k=k+1,继续计算。
3 实验仿真与结果分析 31 实验模型为了进一步验证算法的有效性,本文引用如下的模型[10],该模型在大量文献中均可看到,是研究比较各种粒子滤波算法性能的典型验证模型之一。
状态模型和观测模型分别为
| ${x_{k + 1}} = 0.5x + \frac{{25x}}{{1 + {x^2}}} + 8\cos 1.2\left( {k - 1} \right) + {w_k}$ |
| ${y_k} = \frac{{{x_k}^2}}{{20}} + {v_k}$ |
式中:k表示状态时刻,xk表示状态量,yk表示观测量,状态初始值为x0=0.1 ,wk 、vk均服从零均值高斯分布,方差分别为Ó2m和Ó2n,状态变量xk为一维变量,初始状态x
依据上述模型中的系统方程与测量方程,设定初始时刻状态值x0和粒子总数,神经网络的学习步长为0.05,神经元个数为6,过程噪声方差Q=1、量测噪声方差R=1时。运行环境为MATLAB R2009a,Intel Core(TM) 2 Duo CPU T6500,2.1 GHz,2 G 内存。为了对比不同粒子数目的实验结果,选取50、100、150个粒子,结果如图 2~7所示。
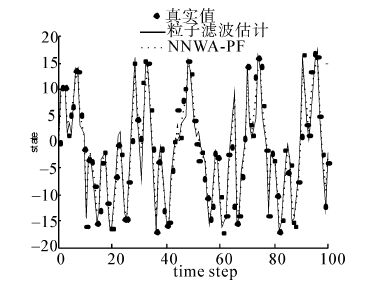
|
| 图 2 粒子数为50时算法结果对比情况 Fig. 2 Comparison of the algorithms under the condition of 50 particles |

|
| 图 3 粒子数为50时误差对比情况 Fig. 3 Error comparison under the condition of 50 particles |

|
| 图 4 粒子数为100时算法结果对比情况 Fig. 4 Comparison of the algorithms under the condition of 100 particles |

|
| 图 5 粒子数为100时误差对比情况 Fig. 5 Error comparison under the condition of 100 particles |
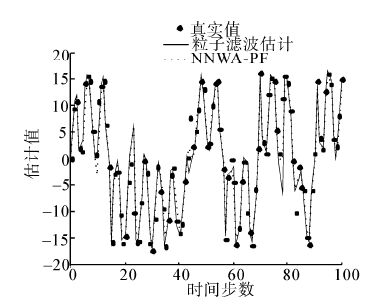
|
| 图 6 粒子数为150时算法结果对比情况 Fig. 6 Comparison of the algorithms under the condition of 150 particles |

|
| 图 7 粒子数为150时误差对比情况 Fig. 7 Error comparison under the condition of 150 particles |
从图中可以看出,BP神经网络辅助的粒子滤波算法比基本粒子滤波算法对状态的估计性能更好。2种算法处理后的不同参数如表 1所示。
| 算法 | 粒子数 | 平均有效样本 | RMSE |
| PF | 50 | 22.865 0 | 3.816 3 |
| NNWA-PF | 50 | 30.415 5 | 3.539 9 |
| PF | 100 | 41.841 4 | 3.517 8 |
| NNWA-PF | 100 | 48.120 9 | 3.175 0 |
| PF | 150 | 64.551 9 | 3.332 1 |
| NNWA-PF | 150 | 71.265 0 | 3.111 8 |
从表 1不难看出,粒子数目为N=50,NNWA-PF滤波算法的RMSE=3.539 9,基本粒子滤波算法的RMSE=3.816 3。此时,NNWA-PF滤波算法的有效样本为30.415 5。粒子数目为N=100时,NNWA-PF滤波算法的RMSE=3.175,基本粒子滤波算法的RMSE=3.517 8。此时,NNWA-PF滤波算法的有效样本为48.1209。粒子数目为N=150时,NNWA-PF滤波算法的RMSE=3.111 8。此时,NNWA-PF滤波的有效样本为71.265 0。从中可以看出引入神经网络后的重要性权值调整粒子滤波算法能有效地抑制样本退化,而且,在同等条件下,有效样本数目增多,方差越小,估计精度越高。
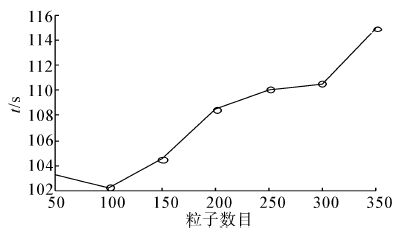
为了验证不同算法复杂度与粒子滤波中粒子个数N的关系,分别选取50,100,…,350个粒子,仿真其运行时间(单位:s),得到的结果如图 8、9所示。
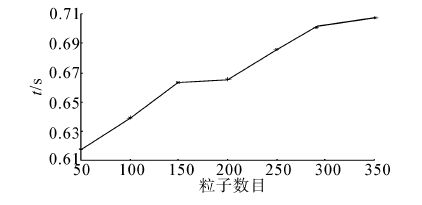
|
| 图 8 粒子滤波算法运行时间与粒子数目的关系 Fig. 8 Relation of PF running time and number of particle |
从图 8和图 9中可看出,基本粒子滤波算法的运行时间随着粒子数目的增加基本成线性增长。NNWA-PF的运行时间随着粒子数目的增加成非线性增长。
|
| 图 9 NNWA-PF算法运行时间与粒子数目的关系 Fig. 9 Relation of NNWA-PF running time and number of particle |
将BP神经网络和基本粒子滤波算法有机结合,通过理论分析和数学仿真,比较了相同粒子数样本条件下,BP神经网络辅助的粒子滤波与基本粒子滤波的有效粒子数目和均方根误差参数,分析了不同粒子数目条件下算法的复杂度。结果表明:神经网络辅助的粒子滤波算法有效地改善了滤波性能,降低了估计方差,同时,粒子滤波器运行时间均与粒子数目呈递增关系,BP算法的引入增加了算法的运行时间。
| [1] | 程水英, 张剑云. 粒子滤波评述[J]. 宇航学报,2008, 29 (4) : 1099 –1111. |
| [2] | LI P, KADIRKAMANATHAN V. Particle filtering based likelihood ratio approach to fault diagnosis in nonlinear stochastic systems[J]. IEEE Trans Syst, Man, Cybern C,2001, 31 (3) : 337 –343. |
| [3] | GUSTAFSSON F, FREDRIK G. Particle filters for positioning, navigation, and tracking[J]. IEEE Transactions on Signal Processing,2002, 50 (2) : 425 –437. |
| [4] | QING Ming, JO K H. A novel particle filter implementation for a multiple-vehicle detection and tracking system using tail light segmentation[J]. International Journal of Control, Automation and Systems,2013, 11 (3) : 577 –585. |
| [5] | CHEN Zhimin, BO Yuming, WU Panlong, et al. Novel particle filter algorithm based on adaptive particle swarm optimization and its application to radar target tracking[J]. Control and Decision,2013, 28 (2) : 193 –200. |
| [6] | 夏楠, 邱天爽, 李景春, 等. 一种卡尔曼滤波与粒子滤波相结合的非线性滤波算法[J]. 电子学报,2013, 41 (1) : 148 –152. |
| [7] | 陈养平, 王来雄, 黄士坦. 基于粒子滤波的神经网络学习算法[J]. 武汉大学学报:工学版,2006, 39 (6) : 86 –88. |
| [8] | 程洪炳, 黄国荣, 倪世宏, 等. 基于粒子滤波的自组织模糊神经网络算法研究[J]. 仪器仪表学报,2011, 32 (3) : 634 –639. |
| [9] | ARULAMPALAM M S, MASKELL S, GORDON N, et al. A tutorial on particle filters for online nonlinear/non-Gaussian Bayesian tracking[J]. IEEE Transactions on Signal Processing,2002, 50 (2) : 174 –188. |
| [10] | 冯驰, 赵娜. 有效粒子数MCMC粒子滤波算法研究[J]. 应用科技,2009, 36 (4) : 19 –22. |



