2. 重庆邮电大学 数理学院, 重庆 400065
2. Department of Mathematics&Physics, Chongqing University of Post&Telecommunications, Chongqing 400065, China
一直以来,多层前馈神经网络都是国内外学者研究的热点。它具有学习能力强、泛化能力强、稳定性高、结构简单且易于实现等优点,是目前应用最广泛的神经网络模型之一。对它的研究目前主要集中在2个方面:学习算法研究和网络结构优化。由于神经网络结构的设计与最终网络的性能关系密切,一直以来都受到业界人士的广泛关注[1-2]。一方面,如果神经网络的规模太小,虽具有较强的泛化能力,却因未能充分学习训练样本,而导致对复杂问题处理能力不够;另一方面,如果网络的规模太大,此时网络学习训练样本性能虽好,却会降低网络的计算效率,且容易产生“过拟合”现象,致使网络泛化能力下降。为了解决神经网络结构优化问题,近年来学者们提出了许多优化方法:1) 试凑法,由网络模型来查找出优化结构,通过训练和比较不同结构的方法来实现网络结构优化的目的,用得较多的方法有:1) 交叉校验[3-4],此法虽简单易行,但需要若干个候选网络,所以过程繁琐费时,且易陷入局部极小值;2) 修剪法[5-6],比较著名的是最优脑外科算法(OBS),通过初始化构造一个有冗余节点的网络,并逐渐除去对网络输出贡献较小的节点,以达到误差精度的要求,此法虽可以降低网络复杂性,提高网络的泛化能力,但它是通过逐个删除具有最小特征值的权值来实现对网络结构的修剪,大大增加了程序计算量和运行时间;3) 遗传进化算法[7-8],通过在解空间的多个点上进行全局搜索,对神经网络的各种群分别实施选择、交叉、变异等相关遗传操作,产生新的子种群并从中选出最优个体组合代表整个网络,具有较强的搜索能力和较强的鲁棒性,不足之处是权重编码长度过长导致搜索效率低下。
针对上述问题,将BP算法、合作型协同进化遗传算法(CCGA)和显著性修剪算法有机结合,提出了基于显著性分析的神经网络混合修剪算法,并将其应用于股票市场的预测上。通过相关实验对比,表明了该结构优化方法的有效性。
1 混合修剪算法遗传算法是一种求解最优化问题的全局搜索算法。它可以优化神经网络权值,但同时优化神经网络的结构和权值效果并不明显。而近年来出现的合作型协同进化遗传算法却能够很好地同时优化神经网络的结构和权值。因此,笔者首先采用合作型协同进化遗传算法优化神经网络的结构和权值,将待优化神经网络进行分割,把一个复杂的神经网络分割为多个相互关联的相对简单的子神经网络,并对分割后的多个子神经网络进行编码,形成多个子种群,各个子种群独立实施遗传操作,如选择、交叉和变异等。在进化过程中,只在进行个体评价时,各个子种群间才有信息交换,因为待优化的神经网络是由来自不同种群的个体共同组成的,各子种群只有相互合作才能共同进化,从而完成相应的优化任务。同时在优化的过程中,利用显著性分析方法和启发式结构优化方法来修剪神经网络,从而降低算法的计算复杂性,并提高收敛速度。
1.1 种群分割假设要优化的神经网络包含p+2层,也就是说有1个输入层、p个隐含层和1个输出层。由于股票市场本身是一个非线性问题,只有2层的神经网络是一种感知器神经网络,它不能用在股票这种非线性问题的预测上。所以,在此把3层的子神经网络做为一个模块,它是一个包含输入层、隐层、输出层的完整的神经网络模型,这种划分方式既保存网络的完整性,又提高了网络的性能。因此,本文对该神经网络进行纵向分割,如图 1所示,从第1层(输入层)到第3层(第2个隐含层)之间的部分为第1个模块,第2层(第1个隐含层)到第4层(第3个隐含层)之间的部分为第2个模块,第p层(第p-1个隐含层)到第p+2层(输出层)之间的部分为第p个模块。对一个模块,采用一个进化子种群优化结构和连接权值,这些进化子种群分别记为P1,P2,...,Pp,因此,共有p个进化子种群,也就是说合作型协同进化遗传算法包含的子种群个数为p。
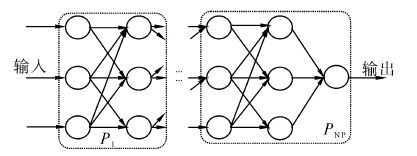
|
| 图 1 种群分割图 Fig. 1 Population segmentation |
不失一般性,现在考虑神经网络的第p个模块,它是第p层到第p+2层之间的部分,由第p个进化子种群优化,为了同步优化网络结构和权值,对其结构采用二进制编码,仅考虑有连接关系的神经元,这样能减小编码长度;连接权值采用实数编码,避免了采用二进制编码对权值表示精度的限制。
1.2.1 结构编码设第p个模块有M个神经元,序号是从1到M排列的输入层(第p层)、隐层(第p+1层)、输出层节点(第p+2层)。将第p个模块的连接关系用矩阵表示,即SM×M。在矩阵中,S(i,j)的元素表示从第i个神经元到第j个神经元的连接关系,“0”表示没有连接,“×”表示没有关联,“1”表示有连接。因此,可以用矩阵SM×M表示第p个模块进化子种群的个体的拓扑结构编码。同时,可以将该矩阵按自左到右、自上而下顺序连接起来,展开成二进制串。下面以图 2所示结构展开说明。

|
| 图 2 神经网络编码图 Fig. 2 Neural network coding |
以图 2为例,则2个子网的结构编码矩阵依次为
| ${S_1} = \left[ {\begin{array}{*{20}{c}} \times & \times & \times & \times & \times & \times & \times \\ \times & \times & \times & \times & \times & \times & \times \\ 1&0& \times & \times & \times & \times & \times \\ 1&1& \times & \times & \times & \times & \times \\ 1&1& \times & \times & \times & \times & \times \\ \times & \times &1&0&1& \times & \times \\ \times & \times &0&1&1& \times & \times \end{array}} \right]$ |
该矩阵等价于结构码串:10 11 11 101 011;
| ${S_2} = \left[ {\begin{array}{*{20}{c}} \times & \times & \times & \times & \times & \times \\ \times & \times & \times & \times & \times & \times \\ \times & \times & \times & \times & \times & \times \\ 1&0&1& \times & \times & \times \\ 0&1&1& \times & \times & \times \\ \times & \times & \times &1&1& \times \end{array}} \right]$ |
该矩阵等价于结构码串:101 011 11。
1.2.2 权值编码如果两节点之间没有连接关系,则其连接权值一定为0。因此,没有必要考虑该连接权值的编码,这样,连接权值受结构编码控制,只有结构编码为1,才考虑连接权值的编码,并且连接权值编码的长度等于结构编码中1的个数。当然,随着结构编码变化,连接权值编码的长度也随着不断变化,这种动态编码方法能够有效地降低算法的计算复杂性。仍以图 2为例,相应的权值编码如下:
| $\begin{array}{l} {S_1} \to - 1,1, - 3, - 2,1,3, - 1, - 2,1,\\ {S_2} \to 3, - 1, - 2,1,1, - 2 \end{array}$ |
由于笔者进化子种群的个体编码包括结构部分和连接权值部分,并且不同部分采用的编码方式不同,因此,需要设计相应的遗传操作。对于结构部分,由于采用二进制编码,利用标准遗传算法中的交叉操作,如单点交叉、多点交叉或一致交叉等;对于连接权值部分,由于采用实数编码,且实数编码的长度等于结构编码中1的个数,因此,实数编码串的交叉点应该依赖于结构部分交叉点的位置。更确切地讲,实数编码交叉点前的串长应该等于相应的结构编码交叉点前1的个数,即所谓的对等交叉。
仍以图 2为例,考虑第2子种群的2个父代个体,它们的编码如图 3(a)。对于结构部分,随机选取第4位作为交叉点,即101 011 11和011 111 01,得到的交叉操作后的子代个体的结构部分为101 001 01和011 111 11;对于连接权值部分,交叉点的选取如图 3(b)所示,得到的交叉操作后的子代个体的连接权值部分为3,-1,-2,-1和2,-3,1,-2,1,1,-2;因此,交叉操作后2个子代的编码如图 3(c)。

|
| 图 3 交叉操作图 Fig. 3 Crossover operation chart |
同样,分别考虑进化个体的结构部分和连接权值部分。对于结构部分,采用标准遗传算法的变异操作,如单点变异、多点变异或一致变异等;对于连接权值部分,由于其编码受结构部分的影响,因此当结构部分某位的编码由1变异为0时,相应的连接权值部分的编码应该删除。反之,当结构部分某位的编码由0变异为1,相应的连接权值部分的编码应在一定范围内随机生成。根据结构部分的变异结果,对调整后的连接权值部分采用非一致变异操作,实现其变异[9]。这样,使该算法具有局部随机搜索能力,同时维持种群多样性。
1.4 基于显著性分析的神经网络结构优化符号说明:λ为拉格朗日乘子;H为Hessian矩阵;w为连接权值;Δw为权值平均值增量;li为除了第i个元素为1以外其他元素均为零的单位向量;wij为与神经元i相连的第j个连接权值;Eav为误差函数。
显著性分析算法是基于误差函数Eav的泰勒级数展开模型,将最小化的性能函数用误差函数Eav(w)表示。在训练过程中,根据误差函数Eav(w)的要求不断调整网络权值w,利用所有与第i个隐层神经元相连接权值的均值来计算其显著性Si大小,除去Si较小的神经元,从而达到修剪网络的目的。
假设神经网络已训练并趋于局部极小,可得:
| $\Delta {E_{{\rm{av}}}}{\rm{ = }}{\left( {\frac{{\partial {E_{{\rm{av}}}}}}{{\partial w}}} \right)^T}\Delta w + \frac{1}{2}\Delta {w^T}H\Delta w + R\left( {{{\left\| {\Delta w} \right\|}^3}} \right)$ | (1) |
因为网络已训练并趋于局部极小点,所以可以将式(1) 的一阶项去掉,并忽略高阶项,得到
| $\Delta {E_{{\rm{av}}}}{\rm{ = }}\frac{1}{2}\Delta {w^T}H\Delta w$ | (2) |
由此,可得到其Hessian矩阵:
| ${H_{i,i}} = \frac{{{\partial ^2}\Delta {E_{{\rm{av}}}}\left( {{w_i}} \right)}}{{{\partial ^2}{w_i}}}$ | (3) |
式(3) 中是对H中的某一连接权值wi进行的,为减少计算量,利用与第i个神经元相连接的所有k个权值平均值wi来进行计算,令${{\bar w}_i} = \sum\limits_{j = 1}^k {{w_{ij}}/k} $,则式(3) 可写成:
| ${H_{i,i}} = {\partial ^2}\Delta {E_{{\rm{av}}}}\left( {{{\bar w}_i}} \right)/{\partial ^2}{{\bar w}_i}$ | (4) |
为了便于分析隐层神经元的显著性,先引入拉格朗日函数:
| $S = \frac{1}{2}\Delta {{\bar w}^T}H\Delta \bar w - \lambda \left( {l_i^T\Delta \bar w + {{\bar w}_i}} \right)$ | (5) |
利用矩阵的逆,求得S关于Δw的导数,权向量w中的最佳变化为
| $\Delta \bar w = \frac{{{{\bar w}_i}}}{{{{\left[ {{H^{ - 1}}} \right]}_{i,i}}}}{H^{ - 1}}{l_i}$ | (6) |
其对应的第i个神经元的显著性可表示为
| ${S_i} = {{\bar w}_i}{}^2/2{\left[ {{H^{ - 1}}} \right]_{i,i}}$ | (7) |
以下是显著性分析修剪算法概要:
1) 训练给定的相对复杂的初始神经网络,使得网络均方误差趋于局部极小值。
2) 计算Hessian矩阵的逆H-1。
3) 计算每个隐层神经元i 的显著性Si,如果Si的值远小于均方误差Eav,那么删去相应的神经元,再转到4);否则,转到5)。
4) 根据式(6) 对网络中所有连接权值进行调整校正,再转到2)。
5) 当网络中不再有可被除去神经元时,终止。
同时,在优化的过程中,可以利用神经网络的知识,降低优化算法的计算量。由于进化个体的结构编码与神经网络的某一模块的连接关系一一对应,而这一结构编码是采用矩阵来表示的。有些矩阵的形式比较特殊,它的某一行可能全部为零,或某一列可能全部为零,或两者皆有。例如考虑类似于图 2所示的神经网络,图 4(a)和(b)是其2个模块编码的矩阵,对应的模块结构分别是图 4(c)和(d)。

|
| 图 4 神经网络结构优化 Fig. 4 Neural network structure optimization |
首先,考虑图 4(a),在矩阵S1中全为0的行对应的第3个节点没有输入,且这一节点在隐含层,这在神经网络中不应该出现,应该删除该节点。再考虑图 4(b),在矩阵S2中全为0的列对应的第5个节点没有输出,且这一节点也在隐含层,这在神经网络中也不应该出现,应该删除该节点。删除这些节点,意味着相应的连接权值也被删除。因此,进化个体编码的长度将会缩短,从而有效地降低算法的复杂性。
在计算某进化子种群的个体的适应度时,首先检查该进化个体的结构部分,如果有为0的行或列,就调整合作团体中相应的代表个体的结构编码。具体地讲,当Sp的第k行(列)为0时,相应的节点应被删除,代表个体Sp+1相应的节点也应该被删除;当Sp结构部分编码变化后,代表个体Sp+1的连接权值部分的编码也应变化,即删除相应的连接权值编码。
与本文工作密切相关的参考文献[6]所提出的感知器神经网络显著性修剪算法,而本文的方法主要是在引入合作型协同进化神经网络的同时,融合了启发式修剪算法。这种混合修剪算法对于神经网络的优化效果更佳。用显著性修剪的多层感知器神经网络,虽是一种具有很好的非线性映射能力的多层前馈神经网络模型,但它采用的是BP算法。因此,网络收敛速度较慢且容易陷入局部极小值。而所引入的合作型协同进化神经网络,它融合了遗传算法和BP算法等方法,优势互补,很好地克服这些不足,且在非线性问题的处理上更显其优势。
1.5 适应度函数及代表个体选择个体适应度值计算公式[10]为
| $f = \frac{1}{{\frac{1}{T}\sum\limits_{p = 1}^T {\sum\limits_{i = 1}^n {{{\left( {{t_{pi}} - {y_{pi}}} \right)}^2}} } + \alpha }}$ | (8) |
式中:tpi和ypi分别表示第p个样本,神经网络的第i个输出单元的期望输出和实际输出;T为样本总数;n为神经网络的输出单元数;α为一个小的正数,它能够保证整个分母不为0,取值可以取α≥10-4。
在合作型协同进化遗传算法中,代表个体的选择非常重要。Potter[11]给出了2种代表个体的选择方法: 1) 直接选择其他进化种群当前代最优个体为代表个体;2) 从其他子种群中选择2个个体作为代表个体,分别为当前代的最优个体和随机选择子种群中的一个个体。其中,前者计算量较小,在子种群相关性不大的问题中适用;而后者适用于子种群相关性较大的问题。由于笔者考虑的神经网络的各个模块之间的输入输出是密切相关的,因此,这里选择后者。
1.6 算法流程笔者提出的基于显著性分析的神经网络混合修剪算法,采用合作型协同进化遗传算法优化神经网络,同时在确定神经网络结构的时候,引入显著性分析方法,对显著性较小的各神经元进行修剪,实现对网络结构的调整,以此简化神经网络结构。基于显著性分析的神经网络混合修剪算法的相应步骤为:
1) 创建一个初始的神经网络,将待优化神经网络分割成p个模块P1,P2,...,Pp。
2) 当t=0时,在每个子种群各自搜索空间里,初始化p个进化子种群P1(t),P2(t),...,Pp(t)。
3) 对每个进化子种群的个体,选择其代表个体,将其组合成一个合作团体,解码后得到相应的神经网络,依式(8) 计算适应度。
4) 按照笔者所述方法,实施交叉和变异操作,优化神经网络的结构,保留最优个体,形成下一代进化子种群。
5) 判定是否满足算法终止条件(即网络误差足够小或达到进化代数)。若满足,进化结束,并输出优化后的神经网络;否则t=t+1,转到3)。
2 票价格预测仿真股影响股票价格预测的因素相当多,比如开盘价、收盘价、成交量等历史基本信息,也有MA5、MA10、KDJ等经过处理后能间接反应出股票走势趋向的信息。本文选取开盘价、最高价、最低价、收盘价、成交量、涨跌幅、MA5、MA10等8个指标作为输入项。选择上证综指(000001) 和中国石化(600028) 作为研究对象,数据来源为大智慧软件收集的2012年7月12日-2013年5月27日之间的210个交易日数据作为原始数据。其中前200组数据作为训练样本,分别用来训练GA-BP神经网络、基于显著性修剪的多感知器神经网络(FOBS)、修剪前的CCGA-BP神经网络、修剪后的CCGA-BP神经网络(HCCGA-BP),后10组数据的收盘价作为预测数据,来验证所训练网络的预测性能。
2.1 数据预处理由于原始数据单位不同,数据大小也有很大差别,同时原始数据中包含有一些不确定的属性值,比如噪声,为了减少这些因素对预测结果的影响,需要先对原始数据进行归一化预处理,其转换公式为
| ${{x'}_i} = \frac{{{x_i} - \min x}}{{\max x - \min x}}$ | (9) |
式中:max x和min x分别表示样本数据中最大值和最小值,xi表示原始数据,x′i表示预处理后范围在[0,1]内的数据。
2.2 性能评价指标为了检验预测结果,需要设定一些评价的标准,在此主要使用均方误差与正确趋势率。
1) 均方误差(MSE)。
假设系统预测值为Yi,对应的实际值为Ti,预测误差为Ei,且Ei=Yi-Ti,则
| ${\rm{MSE}} = \frac{1}{n}\sum\limits_{i = 1}^n {E_i^2} $ | (10) |
2) 正确趋势率(PCD)。
所谓的正确趋势率,是将连续的2次预测值的变化趋势和实际值的变化趋势相比较,若变化方向一致,即都是降价、不变或都是涨价,则变化趋势正确;否则,变化趋势不正确。定义如下:
| ${\rm{PCD}} = \sum\limits_i {{\rm{pc}}{{\rm{d}}_i}/N} $ | (11) |
式中:${\rm{pc}}{{\rm{d}}_i} = \left\{ \begin{array}{l} 1\left( {{Y_{i + 1}} - {Y_i}} \right)\left( {{E_{i + 1}} - {E_i}} \right) > 0\\ 0\left( {{Y_{i + 1}} - {Y_{ii}}} \right)\left( {{E_{i + 1}} - {E_i}} \right) \le 0 \end{array} \right.$。
2.3 实验结果分析选取适当的初始网络,将促使所得网络更加简单、学习速度更快和归纳性更好。相关研究[12]表明:具有S形函数的非线性3层神经网络结构,可以逼近任何的非线性函数,但是,在这种只有单个隐层的神经网络里,各个神经元之间相互影响,不利于函数逼近性的改进;而Blum和Li[13]通过实验证明:拥有2个隐层的神经网络,其全局函数逼近性更好,且更易于改进。因此,在本文中,笔者采用4层的BP神经网络预测模型,输入层有上述的8个节点,输出层只有一个节点,表示的是下一个交易日收盘价。采用的HCCGA算法包含2个种群,分别为输入层——隐层1——隐层2和隐层1——隐层2——输出层。运用MATLAB7.0作仿真实验预测,其中相关参数设置为:种群大小设为10,最大进化代数设为100,交叉概率设为0.4,结构变异概率与权值变异概率分别设为0.002和0.03。
将上述学习后的神经网络应用到上证综指(000001) 和中国石化(600028) 的预测上,下面是结果分析。
2.3.1 HCCGA-BP与FOBS预测结果比较图(5)、图(6)分别是上证综指(000001) 和中国石化(600028) 的预测收盘价格。
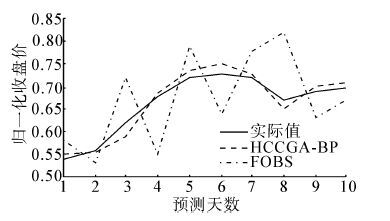
|
| 图 5 上证综指(000001) 预测收盘价格 Fig. 5 SHCOMP (000001) closing price |

|
| 图 6 中国石化(600028) 预测收盘价格 Fig. 6 SINOPEC (600028) closing price |
从预测的结果可以看出,所采用的神经网络结构可以较为理想地逼近上证综指(000001) 和中国石化(600028) 的运行情况,正确趋势率(PCD)均大于 90%,均方误差(MSE)分别从0.007 3减小到0.000 24,从0.013 46减小到0.001 1。由此可见,该神经网络结构对于股票的预测拟和度较高,具有较高的预测精度。同时从表 1和表 2中看到,基于显著性分析的神经网络混合修剪算法极大地提高了系统的收敛速度,同时也明显地提高了预测精度。
| MSE* | PCD/% | 迭代代数 | 计算时间/s | |
| FOBS | 0.007 30 | 62.1 | 7 632 | 86.5 |
| HCCGA-BP | 0.000 24 | 92.1 | 6 421 | 78.2 |
| 注:归一化 | ||||
| MSE* | PCD/% | 迭代代数 | 计算时间/s | |
| FOBS | 0.013 46 | 67.3 | 6 215 | 71.2 |
| HCCGA-BP | 0.001 10 | 90.4 | 5 842 | 62.3 |
| 注:归一化 | ||||

|
| 图 7 上证综指(000001) 预测均方误差对比 Fig. 7 SHCOMP (000001) error comparison |
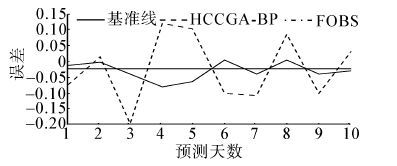
|
| 图 8 中国石化(600028) 预测均方误差对比 Fig. 8 SINOPEC (600028) error comparison |
通过对比实验可知,基于显著性分析的神经网络混合修剪算法比FOBS算法不仅在收敛速度上有明显提高,而且在预测精度和误差上也有明显提高。因此,与基于显著性修剪的多感知器神经网络(FOBS)对于股票的预测相比,HCCGA-BP神经网络在收敛速度、预测精度、误差对比上的优势,都说明该预测模型的有效性。
2.3.2 HCCGA-BP与CCGA-BP、GA-BP预测结果比较图 9、图 10分别是上证综指(000001) 和中国石化(600028) 的预测收盘价格。
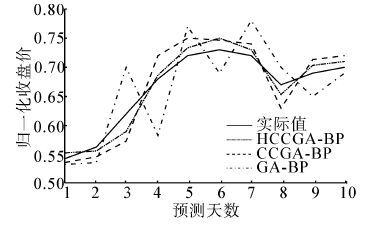
|
| 图 9 上证综指(000001) 预测收盘价格 Fig. 9 SHCOMP (000001) prediction cosing price |

|
| 图 10 中国石化(600028) 预测收盘价格 Fig. 10 SINOPEC (600028) prediction closing price |
从上面的预测图(图 9、图 10)、误差对比图(图 11、图 12)及性能比较表(表 3、表 4)可以看出,所采用的神经网络结构可以较为理想地逼近上证综指(000001) 和中国石化(600028) 的运行情况。

|
| 图 11 上证综指(000001) 预测均方误差对 Fig. 11 SHCOMP (000001)prediction error comparison |

|
| 图 12 中国石化(600028) 预测均方误差对比 Fig. 12 SINOPEC (600028) prediction error comparison |
| MSE* | PCD/% | 迭代代数 | 计算时间/s | |
| GA-BP | 0.002 74 | 69.3 | 8 153 | 93.8 |
| CCGA-BP | 0.000 86 | 87.4 | 7 524 | 82.6 |
| HCCGA-BP | 0.000 24 | 92.1 | 6 421 | 78.2 |
| 注:归一化 | ||||
| MSE* | PCD/% | 迭代代数 | 计算时间/s | |
| GA-BP | 0.006 3 | 71.9 | 6 843 | 74.6 |
| CCGA-BP | 0.001 9 | 86.2 | 6 216 | 68.2 |
| HCCGA-BP | 0.001 1 | 90.4 | 5 842 | 62.3 |
| 注:归一化 | ||||
相比之下,修剪后的HCCGA-BP神经网络的均方误差(MSE)比修剪前的CCGA-BP神经网络、GA-BP神经网络的均方误差(MSE)要小得多;正确趋势率较高;迭代代数和计算时间也相对较少。
实验结果表明,神经网络经过大量和充分的训练之后,确实在外部形式上拟和了数据,在股市数据内部总结出了所蕴藏的变化规律。与CCGA-BP神经网络、GA-BP神经网络相比,基于显著性分析的神经网络混合修剪算法模型对于股票的预测,无论是在收敛速度,还是在预测精度以及误差对比上,都说明混合修剪算法预测模型的有效性。
3 结束语笔者针对神经网络结构问题,提出了基于显著性修剪的合作型神经网络,并将其应用到股票预测上。通过实验结果比较可知,该模型很适合解决股票市场这样的非线性问题。与传统遗传神经网络模型相比,避免传统遗传神经网络编码方案过长、结构优化不明显、计算量大等不足;相比之下,该算法对股票预测结果更为精确。由此证明了该算法模型的有效性,有一定的实用价值。然而,股票本身是一个非常复杂的动态非线性系统,影响因素众多,比如国家经济政策、市场本身的影响等都会对其走势产生一定的影响,而且所选取的输入数据很多都是主观确定的,缺乏股票预测理论的指导;同时,该算法也一定的局限性,如对实际优化问题的决策变量进行了人为的分解、代表个体的选择等,这些方面都需要一定程度上的改进。虽然改进模型提高了预测精度,但也只能给投资者提供一些参考意见。
| [1] | YONG Mingjing, HUA Yingdong. Study on characteristic of fractional master-slave neural network[C]//Fifth International Symposium on Computational Intelligence and Design. Hangzhou, China, 2012: 498-501. |
| [2] | 乔俊飞, 张颖. 一种多层前馈神经网络的快速修剪算法[J]. 智能系统学报,2008, 3 (2) : 622 –627. QIAO Junfei, ZHANG Ying. Fast unit pruning algorithm for feed forward neural network design[J]. CAAI Transactions on Intelligent Systems,2008, 3 (2) : 622 –627. |
| [3] | MOOD Y J. Prediction risk and architecture selection for neural networks[C]//Statistics to Neural Networks: Theory and Pattern Recognition Applications, NATO ASI Series F. New York, 1994: 288-290. |
| [4] | LIU Yong. Create stable neural networks by cross-validation[C]//International Joint Conference on IJCNN'06 Neural Networks. Vancouver, Canada, 2006: 3925-3928. |
| [5] | DU Juan, ER Mengjoo. A fast pruning algorithm for an efficient adaptive fuzzy neural network[C]//Eighth IEEE International Conference on Control and Automation. Xiamen, China, 2010: 1030-1035. |
| [6] | 乔俊飞, 韩红桂. 前馈神经网络分析与设计. 北京:科学出版社[M]. 2013 : 107 -158. |
| [7] | EUGENE S, MARIA S. A self-configuring genetic programming algorithm with modified uniform crossover[C]//WCCI 2012 IEEE World Congress on Computational Intelligence. Brisbane, Australia, 2012: 1984-1990. |
| [8] | 吴鹏. 基于语法引导的遗传编程在神经树中的应用[D]. 济南: 济南大学, 2007: 69-102. WU Peng. The application of genetic programming in the neural tree based on grammar guide[D]. Jinan: University of Jinan, 2007: 69-102. |
| [9] | 周明, 孙树栋. 遗传算法原理及应用. 北京:国防工业出版社[M]. 1999 : 1 -26. |
| [10] | 巩敦卫, 孙晓燕. 基于合作式协同进化算法的神经网络优化[J]. 中国矿业大学学报,2006, 35 (1) : 114 –119. GONG Dunwei, SUN Xiaoyan. Optimization of neural network based on cooperative co-evolutionary algorithm[J]. Journal of China University of Mining&Technology,2006, 35 (1) : 114 –119. |
| [11] | POTTER M A. The design and analysis of a computational model of cooperative co-evolution [D]. Fairfax: George Mason University, 1997: 21-66. |
| [12] | HETCHT N R. Theory of the back propagation neural network[C]//Proceedings of the International Joint Conference on Neural Networks. New York: IEEE Press, 1989: 593-611. |
| [13] | BLUM E K, LI L K. Approximation theory and feed forward networks[J]. Neural Net,1991, 2 (3) : 511 –515. |



