随着公共交通的大力发展,综合交通枢纽已成为城市交通系统中的重要节点,人们对城市交通枢纽活动空间的舒适、便捷、高效等有了更高的需求。在我国的大型综合交通枢纽中,乘客流密度高、流动性大,交织冲突明显,在这种空间下,极易造成枢纽内乘客的拥挤、滞留,增加了踩踏事故发生的机率。因此,及时、准确地掌握客流信息,正确评价乘客流的状态,实现实时信息发布和动态诱导,不但可以使相关管理部门掌握乘客流的真实状况,有针对性地组织预警,更好地解决乘客流拥挤问题,而且可以使乘客了解枢纽内的拥挤状况,自觉规避拥挤和风险,从而有效地改善枢纽内的乘车环境,提高乘客在枢纽中的通行速度,缓解大客流带来的运输组织压力,保障乘客的出行安全。因此,对城市公共交通枢纽内乘客流状态评价的研究有着重要的现实意义。
根据国内外学者对客流运行状态评价方法[1-3]研究以及对机动车交通状态评价方法[4-6]研究可知,行人的微观特性、排队长度、行程时间等直观行人交通参数,使用目前的检测技术不能达到精度要求;数据包络分析法(DEA)以及应用熵理论的综合评价方法等复杂算法中部分指标难以实现实时的计算,不适合对客流运行状态的动态评价。本文提出了一种客流拥挤指数的指标来评价枢纽内客流状态,并基于行人密度和单位宽度流率建立综合模糊评价模型获得客流拥挤指数,通过针对北京某一枢纽站内的客流状况的仿真,所得结论与《行人交通》标准评价结果相吻合。
1 客流拥挤指数枢纽内客流状况的评价一般包括以下几个步骤:首先确定评价目标,本文以城市公共交通枢纽客流运行状况为评价目标;其次,建立评价指标,要在众多影响、反映客流运行状况的变量中选取具有代表性、相对独立的因素,来综合建立科学的评价指标;然后确定综合评价方法,根据各指标的特性及其对总目标的影响来选择最佳方法;最后,依据所选定的方法确定相应评价指标,本文中选定拥挤指数作为评价枢纽内客流运行状况的评价指标。
本文所提出的客流拥挤指数,类似“空气污染指数”和“交通拥堵指数”,是一种能够综合反映枢纽运行状态定量化的相对数,是一种反映特定时刻、特定区域的拥挤程度和差别量化的相对数,是一种把复杂现象简单化的相对数[7]。其本质上呈现了在较长时间内枢纽客流运行的拥挤程度、趋势和规律,主要用来评价枢纽内的运行状态。
枢纽内客流运行状态可分为畅通和拥挤2种状态。根据拥挤程度又可以分为轻度拥挤、中度拥挤和严重拥挤,畅通可分为畅通和基本畅通。
1) 畅通状态:有足够的空间可供行人自由选择行走速度及赶超其他行人的机会;
2) 基本畅通状态:行走速度可自由选择,但赶超其他行人受到轻微的限制,反向人流和横向穿越时会造成一些冲突;
3) 轻度拥挤状态:行走速度不能自由选择,赶超其他行人受到限制,反向人流和横向穿越时会造成显著冲突;
4) 中度拥挤状态:所有行人的速度和赶超其他行人的可能性均受到限制,前进速度缓慢,反向行走和横向穿越极其困难;
5) 严重拥挤状态:行走速度严重受限,与其他行人经常不可避免地发生冲突,几乎不可能反向行走和横向穿越,人流是不间断、不稳定的。
针对上面5种客流状态,本文用一种[0,10]的量化数据——枢纽客流拥挤指数来表征当前枢纽的客流状态,分为5个等级。其中0~2、2~4、4~6、6~8、8~10分别对应“畅通”、“基本畅通”、“轻度拥挤”、“中度拥挤”、“严重拥挤”5个级别。
2 客流运行状态评价指标建立客流状态评价指标是对枢纽内运行状态进行分析的基础,是对枢纽内客流拥挤程度评价的前提。评价指标选择的原则就是以尽量少的指标,能够较为全面地反映出枢纽内客流运行状态,并且对客流运行状态变化反应敏感,容易获取且准确率高。一般枢纽内客流运行状态是通过将步行通道、楼梯、排队等候区三大区域的客流运行状态综合反映的。
在运行过程中,乘客流比乘客个体表现出更为复杂的特点,受乘客之间、出行目的和周围环境等影响。要得到全面的客流运行状态,需要通过对客流运行的顺畅程度、稳定程度和空间利用程度三方面进行综合分析[3]。参考针对我国国情的《行人交通》及进一步研究发现,在众多的指标如行人密度、单位宽度流率、速度和负荷度中,行人密度和单位宽度流率能够较为全面地表征步行通道、楼梯和进出站口的客流状态;而对于排队区和候车区用行人密度即可反映出其当前的客流状态。本文以楼梯通道的行人流状况为例进行了较为详细地分析、建模评价和仿真。枢纽内其他区域客流状况的分析、评价方法与此相同,不再赘述。
行人密度是指在道路或排队区域内单位面积的平均行人数量,一般用区域人数和区域面积的比值表示。计算公式如下所示:
| $K = \frac{Q}{{LW}}$ | (1) |
式中:K为行人密度:人/m2;L*W为区域Y的面积;L为区域长度;W为区域宽度;Q为区域Y内的行人数量。
单位宽度流率是指人行道单位有效宽度平均通过的行人数量,计算公式为
| $P = \frac{Q}{{TW}}$ | (2) |
式中:P为单位宽度流率:人/(m·min);W为区域的宽度;Q为T时间内通过区域Y内某一断面的行人数量。
行人密度与行人占据空间互为倒数。据统计,我国成年人静止时垂直投影面积约为0.18 m2。由心理学家所做的人类缓冲区域测量实验可知,行人与行人或设施之间需要保持一定距离的缓冲空间,其最低要求范围为0.22~0.26 m2;行人在楼梯通道内行走时需要0.7 m2的活动空间,当行人占据空间在0.4 m2时,行走速度严重受到限制,当行人占据空间在0.9 m2以上时,行人以正常速度在楼梯内行走;当行人占据空间在1.4 m2以上时,行人可按自己意愿去行走;当行人占据空间在1.9 m2以上时,行人可以赶超其他行人。按照不同的占用空间对行人有不同的约束,行人对楼梯通道空间需求可以分为: 静态最低需求区域、行动受限区域、行动基本区域、正常行动区域、自由选择速度区域和赶超他人区域6个等级,如表 1所示。
| 类别 | 静态身体 垂直投影 | 静态最低 需求区域 | 行动受 限区域 | 行动基 本区域 | 正常行 动区域 | 自由选择 速度区域 | 赶超他 人区域 |
| 行人占据空间/(m2·人-1) | 0.18 | 0.22 | 0.40 | 0.70 | 0.90 | 1.40 | 1.90 |
| 行人密度 /(人·m-2) | 5.60 | 4.50 | 2.50 | 1.43 | 1.11 | 0.71 | 0.53 |
VISSIM行人仿真模块中,对不同区域内设置不同的输入量,输入量随着时间的增加而不断地增加。通过一段时间的仿真,得到的相似的仿真结果,在12 600 s的仿真时长里,以60 s为一周期,通过3个采集点采集了630组行人交通数据,即行人密度和单位宽度流率。行人密度在2.5 人/ m2左右时,单位宽度流率达到最高。行人密度小于此值时,单位宽度流率随着行人密度的增加而增加,但行人密度高于此单位宽度流率随着行人密度的增加而减少。得出的行人密度与单位宽度流率关系,如图 1所示。
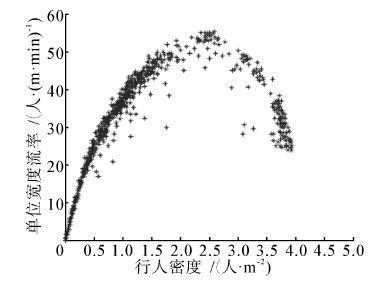
|
| 图 1 行人密度与单位宽度流率关系曲线图 Fig. 1 Relation between pedestrian density and pedestrian flow |
由此可以表明,在行人密度一定时,若P值相对较小,则说明行人流移动缓慢,行人个体或外界干扰因素对行人流的影响大,处理干扰因素带来的影响反应时间短;若P值相对较大,则说明行人流移动相对较流畅,行人与构成的行人流一致性高,行人个体或外界干扰因素对行人流的影响相对较小,处理干扰因素带来的影响反应时间长,可能导致人流停滞。
因此,行人密度和单位宽度流率的大小反映了乘客流在运行过程中对区域空间利用程度、顺畅程度和稳定程度。故本文选用行人流密度和单位宽度流率这2个指标的综合效果来表征枢纽客流运行的顺畅程度、稳定程度、分布均衡程度。
客流在枢纽内各服务设施的各项数据指标,主要参考了反映我国国情的《行人交通》,并综合了美国交通运输研究委员会编写的主要针对公共交通设施服务水平的《Transit Capacity and Quality of Service Manual--2nd Ed》,通过行人密度和单位宽度流率在楼梯通道和步行通道服务水平的阈值来定义的客流拥挤指数。如表 2所示。
| 客流拥挤指数 | 楼梯通道服务水平 | 步行通道(进出站口)服务水平 | 排队和候车区 | ||||
| 行人密度/(人·m-2) | 单位宽度流率/(人·m-1·min) | 行人密度/(人·m-2) | 单位宽度流率/(人·m-1·min) | 行人密度 /(人·m-2) | |||
| A(0~2) | ≤0.71 | ≤23 | ≤0.43 | ≤33 | ≤1.11 | ||
| B(2~4) | 0.71~1.11 | 23~33 | 0.43~0.71 | 33~49 | 1.11~1.43 | ||
| C(4~6) | 1.11~1.43 | 33~43 | 0.71~1.11 | 49~66 | 1.43~3.33 | ||
| D(6~8) | 1.43~2.50 | 43~56 | 1.11~2.00 | 66~82 | 3.33~5.00 | ||
| E(8~10) | >2.50 | Variable | >2.00 | Variable | >5.00 |
3 客流运行状态模糊评价模型
客流拥挤程度是一个模糊的概念,而模糊推理是一种将定性与定量、主观与客观、模糊与清晰相结合的有效评价方法。因此,本文采用模糊推理的方法对枢纽客流运行状态进行评价。
在这里,利用模糊推理的方法就是根据平均行人流密度、平均单位宽度流率和客流拥挤状态之间的关系组成模糊规则矩阵,然后利用平均行人流密度、平均单位宽度流率的实测数据作为输入,通过一系列的模糊运算推断出客流拥挤状态,输出客流拥挤指数。
1) 评判因素集。
楼梯服务水平的评价因素集为:U={ST_K,ST_P},其中,ST_K为行人流密度,ST_P为平均单位宽度流率。
把行人流密度和平均单位宽度流率2个模糊集合的论域定义为
| $\begin{array}{l} {\rm{ST}}\_K = {\rm{ST}}\_P = \left\{ {{\rm 很小},{\rm 小},{\rm 中},{\rm 大},{\rm 很大}} \right\} = \\ \left\{ {{\rm{VS,S,M,L,VL}}} \right\} \end{array}$ | (3) |
2) 评价集。
由于将客流拥挤指数划分了5个等级,故把拥挤状态模糊评价集的论域定义为
| $\begin{array}{l} V = \left\{ {{\rm 畅通},{\rm 基本畅通},{\rm 轻度拥挤},} \right.\\ \left. {{\rm 中度拥挤},{\rm 严重拥挤}} \right\} = \left\{ {A,B,C,D,E} \right\} \end{array}$ | (4) |
3) 隶属函数。
结合设施服务水平及各因素之间的关系及表 1,行人密度隶属函数考虑以下因素进行确定:
当行人密度为0.53 人/m2时,行人可以自由选择速度赶超他人,客流运行状态属于畅通状态,因此小于等于此行人密度值,客流状态就认为是处于畅通状态,隶属度为常值1;
当行人密度在0.71~1.11 人/m2,行人处在自由选择速度区域和正常行动区域之间,客流运行状态属于基本畅通状态,其中点位置的密度0.91,隶属于基本畅通状态的程度最大为1;
当行人密度在1.11~1.43 人/m2,行人处在正常行动区域和行动基本区域,客流运行状态属于轻度拥挤状态,其中点位置的密度1.27,隶属于轻度拥挤状态的程度最大为1;
当行人密度在1.43~2.50 人/m2,行人处在行动基本区域和行动受限区域,客流运行状态属于中度拥挤状态,其中点位置的密度1.96,隶属于中度拥挤状态的程度最大为1;
行人密度大于等于4.5人/m2时,达到了楼梯单位面积可容纳行人的最大值,此时已处于严重拥挤程度状态。因此只要达到这一范围的行人密度值,客流状态就认为是处于严重拥挤状态,隶属度为常值1。
综上,在行人密度低于0.53或大于4.5时,隶属于畅通或严重拥挤特征显著,分别取固定隶属函数为常数1,当行人密度处于这期间的值时,隶属函数分别取不同三角函数,因此,本文采用梯形和三角形相结合的隶属度函数,更符合实际的客流运行状态,如下图 2所示。并根据图 1和表 2行人密度和单位宽度流率之间的关系,确定单位宽度流率的隶属函数。
|
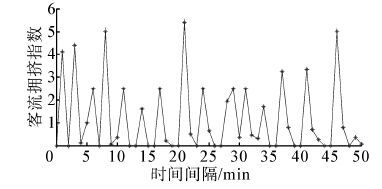
| 图 2 复兴门地铁站客流状态模糊评价结果图 Fig. 2 Fuzzy evaluation result of passenger flow state in Fuxingmen subway station |
行人密度隶属函数如下:
| ${\mu _{{\rm{ST\_K}}}} = \left\{ {\begin{array}{*{20}{l}} {{\mu _{{\rm{K\_VS}}}}\left( x \right) = \left\{ \begin{array}{l} 1,x \le 0.53\\ - 2.63\left( {x - 0.91} \right),0.53 < x \le 0.91 \end{array} \right.}\\ {{\mu _{{\rm{K\_S}}}}\left( x \right) = \left\{ \begin{array}{l} 2.63\left( {x - 0.53} \right),0.53 < x \le 0.91\\ - 2.78\left( {x - 1.27} \right),0.91 < x \le 1.27 \end{array} \right.}\\ {{\mu _{{\rm{K\_M}}}}\left( x \right) = \left\{ \begin{array}{l} 2.78\left( {x - 0.91} \right),0.91 < x \le 1.27\\ - 1.45\left( {x - 1.96} \right),1.27 < x \le 1.96 \end{array} \right.}\\ {{\mu _{{\rm{K\_L}}}}\left( x \right) = \left\{ \begin{array}{l} 1.45\left( {x - 1.27} \right),1.27 < x \le 1.96\\ - 0.39\left( {x - 4.5} \right),1.96 < x \le 4.50 \end{array} \right.}\\ {{\mu _{{\rm{K\_VL}}}}\left( x \right) = \left\{ \begin{array}{l} 0.39\left( {x - 4.5} \right),1.96 < x \le 4.50\\ 1,x > 4.50 \end{array} \right.} \end{array}} \right.$ | (5) |
单位宽度流率隶属函数如下:
| ${\mu _{{\rm{ST\_P}}}} = \left\{ {\begin{array}{*{20}{l}} {{\mu _{{\rm{P\_VS}}}}\left( y \right) = \left\{ \begin{array}{l} 1,y \le 18\\ - 0.1\left( {y - 28} \right),18 < y \le 28 \end{array} \right.}\\ {{\mu _{{\rm{P\_S}}}}\left( y \right) = \left\{ \begin{array}{l} 0.1\left( {y - 8} \right),18 < y \le 28\\ - 0.1\left( {y - 38} \right),28 < y \le 38 \end{array} \right.}\\ {{\mu _{{\rm{P\_M}}}}\left( y \right) = \left\{ \begin{array}{l} 0.1\left( {y - 28} \right),28 < y \le 38\\ - 0.1\left( {y - 48} \right),38 < y \le 48 \end{array} \right.}\\ {{\mu _{{\rm{P\_L}}}}\left( y \right) = \left\{ \begin{array}{l} 0.1\left( {y - 38} \right),38 < y \le 48\\ - 0.1\left( {y - 58} \right),48 < y \le 58 \end{array} \right.}\\ {{\mu _{{\rm{P\_VL}}}}\left( y \right) = \left\{ \begin{array}{l} 0.1\left( {y - 48} \right),48 < y \le 58\\ 1,y > 58 \end{array} \right.} \end{array}} \right.$ | (6) |
4) 模糊规则表。
对模糊评价集(3) 中行人流密度和平均单位宽度流率之间的关系进行分析:
当K是VS时,若P是VS,S和M之一时,行人有足够的空间来选择速度或赶超慢速行人,此时处于畅通状态;若P处于L或VL时,通过区域的客流量很大,但仍有足够的空间,此时属于基本畅通状态。
当K是S时,若P是VS,此时属于畅通状态;若P是S、M、L和VL之一时,行人步行的可用空间充裕,步行速度仍然可自由选择,超越慢速行人受到轻微影响,属于基本畅通状态。
当K是M时,行人可用步行空间开始压缩,赶超慢速行人受到限制,此时属于轻度拥挤状态;若P是VL,此时通过的客流量很大,属于基本畅通状态;当P是VS时,区域的客流通过量很少,属于中度拥挤状态。
当K是L时,此时的行人流速度受到限制,中途停顿时有发生,此时属于中度拥挤状态;若P是VL时,但通过区域的客流量大,属于轻度拥挤状态;若P是VS,此时的行人流的速度很小,行人的步行可用空间受限,通过的客流量很少,属于严重拥挤状态。
当K是VL时,行人流缓慢移动,速度趋于零,基本停滞,此时属于严重拥挤状态。
通过以上对行人流密度和平均单位宽度流率之间的关系分析,可得表 3。
| 行人密度 | 单位宽度流率 | ||||
| VS_P | S_P | M_P | L_P | VL_P | |
| VS_K | A | A | A | B | B |
| S_K | A | B | B | B | B |
| M_K | D | C | C | C | B |
| L_K | E | D | D | D | C |
| VL_K | E | E | E | E | E |
5) 反模糊化方法。
将模糊量转换为精确量的过程,叫做反模糊化,它是模糊化的逆过程。常用的反模糊化方法有:最大隶属度法、面积等分法和重心法。根据反模糊化结果与评价指标的分析对比,采用最大隶属度可以更好地表征二者之间内在联系且计算简便。因此,本文选用最大隶属度平均值法进行模糊评判。
选取推理结果的模糊集合中隶属度最大的元素作为输出值客流拥挤指数,即I=xo=max(μx(x)),x∈V如果输出论域V中,其最大隶属度对应的输出值多于一个,则取所有具有隶属度输出的平均值,即
| $I = {x_o} = \frac{1}{N}\sum\limits_{i = 1}^N {{x_i}} ,{x_i} = \mathop {\max }\limits_{x \in V} \left( {\mu \left( x \right)} \right)$ | (7) |
通过反模糊化得到客流拥挤指数,精确地反映出了区域内的拥挤状况。指数越大说明枢纽内客流运行状态越拥挤,指数越小说明枢纽内客流运行状态越畅通。
4 评价方法及效果仿真验证本实验以实际采集的行人交通数据和以VISSIM仿真采集的行人交通数据分别进行了基于以上提出的模糊客流状况评价方法,对客流状况进行了仿真评价。
1) 基于枢纽内实际采集的客流数据所做的客流状态仿真评价。以北京市复兴门地铁换乘下行楼梯的客流状况为研究对象,通过安装在楼梯处的高清摄像头采集楼梯每分钟的行人交通数据。本实验以2013年1月18日9时20分-10时10分的连续50 min的行人交通数据为基础。
利用MATLAB模糊工具箱,在Simulink里建立以楼梯的行人流密度和平均单位宽度流率作为输入,客流拥挤指数为输出的仿真模型。北京复兴门地铁站的行人交通流数据及评价结果,行人流交通数据(9:21-10:10 1min数据),如表 4,北京复兴门地铁站客流状态模糊评价结果如图 2。
| 时刻 | 客流数据 | 模糊评价结果 | 时刻 | 客流数据 | 模糊评价结果 | ||||||
| 平均 密度 | 单位宽 度人流 | 客流拥 挤指数 | 客流 状态 | 手册等 级对照 | 平均 密度 | 单位宽 度人流 | 客流拥 挤指数 | 客流 状态 | 手册等 级对照 | ||
| 9:21 | 0.11 | 4.12 | 0.00 | 畅通 | A | 9:46 | 0.58 | 15.29 | 0.65 | 畅通 | A |
| 9:22 | 1.13 | 36.86 | 4.10 | 轻度拥挤 | C | 9:47 | 0.07 | 3.14 | 0.00 | 畅通 | A |
| 9:23 | 0.21 | 4.12 | 0.00 | 畅通 | A | 9:48 | 0.30 | 8.82 | 0.00 | 畅通 | A |
| 9:24 | 1.16 | 37.06 | 4.40 | 轻度拥挤 | C | 9:49 | 0.76 | 27.45 | 1.95 | 基本畅通 | B |
| 9:25 | 0.35 | 7.06 | 0.10 | 畅通 | A | 9:50 | 1.08 | 29.61 | 2.50 | 基本畅通 | B |
| 9:26 | 0.62 | 20.78 | 1.00 | 畅通 | A | 9:51 | 0.38 | 14.31 | 0.35 | 畅通 | A |
| 9:27 | 0.92 | 26.47 | 2.50 | 基本畅通 | B | 9:52 | 0.86 | 28.04 | 2.50 | 基本畅通 | B |
| 9:28 | 0.28 | 8.24 | 0.00 | 畅通 | A | 9:53 | 0.49 | 11.76 | 0.45 | 畅通 | A |
| 9:29 | 1.26 | 37.45 | 5.00 | 轻度拥挤 | C | 9:54 | 0.39 | 13.73 | 0.30 | 畅通 | A |
| 9:30 | 0.31 | 7.45 | 0.05 | 畅通 | A | 9:55 | 0.83 | 23.14 | 1.70 | 基本畅通 | B |
| 9:31 | 0.43 | 14.51 | 0.35 | 畅通 | A | 9:56 | 0.02 | 0.59 | 0.00 | 畅通 | A |
| 9:32 | 0.96 | 27.84 | 2.50 | 基本畅通 | B | 9:57 | 0.06 | 0.78 | 0.00 | 畅通 | A |
| 9:33 | 0.20 | 7.84 | 0.00 | 畅通 | A | 9:58 | 1.04 | 32.94 | 3.25 | 基本畅通 | B |
| 9:34 | 0.21 | 8.82 | 0.00 | 畅通 | A | 9:59 | 0.80 | 20.00 | 0.80 | 畅通 | A |
| 9:35 | 0.77 | 22.75 | 1.60 | 基本畅通 | B | 10:00 | 0.23 | 5.88 | 0.00 | 畅通 | A |
| 9:36 | 0.20 | 5.10 | 0.00 | 畅通 | A | 10:01 | 0.25 | 5.69 | 0.00 | 畅通 | A |
| 9:37 | 0.20 | 5.88 | 0.00 | 畅通 | A | 10:02 | 1.07 | 34.12 | 3.35 | 基本畅通 | B |
| 9:38 | 0.99 | 33.73 | 2.50 | 基本畅通 | B | 10:03 | 0.71 | 19.22 | 0.70 | 畅通 | A |
| 9:39 | 0.37 | 11.96 | 0.20 | 畅通 | A | 10:04 | 0.35 | 12.94 | 0.25 | 畅通 | A |
| 9:40 | 0.17 | 3.53 | 0.00 | 畅通 | A | 10:05 | 0.07 | 1.37 | 0.00 | 畅通 | A |
| 9:41 | 0.12 | 9.02 | 0.00 | 畅通 | A | 10:06 | 0.20 | 8.24 | 0.00 | 畅通 | A |
| 9:42 | 1.34 | 41.76 | 5.40 | 轻度拥挤 | C | 10:07 | 1.30 | 42.75 | 5.00 | 轻度拥挤 | C |
| 9:43 | 0.51 | 14.31 | 0.50 | 畅通 | A | 10:08 | 0.65 | 14.90 | 0.80 | 畅通 | A |
| 9:44 | 0.03 | 0.78 | 0.00 | 畅通 | A | 10:09 | 0.06 | 2.35 | 0.00 | 畅通 | A |
| 9:45 | 0.86 | 31.37 | 2.50 | 基本畅通 | B | 10:10 | 0.35 | 13.92 | 0.35 | 畅通 | A |
从实际交通流数据评价结果可知,在50 min内有34个时刻是畅通状态,11个时刻是基本畅通状态,5个时刻是轻度拥挤状态。如在9:39时刻时,行人密度是0.37 人/m2,单位宽度流率是11.96 人/(m·min-1),客流拥挤指数为0.5。对视频处理和分析可以得到,通过的行人数量是61 人,此时行人平均占有空间是2.7 m2,行人可用空间较大,行人速度可自由选择,乘客之间影响较小,可以任意赶超其他行人,处于畅通状态;在9:42时刻,行人密度是1.34人/m2,单位宽度流率是41.76 /(m·min-1),客流拥挤指数为5.6。从视频分析得到,通过的行人数量是213人,此时行人平均占有空间是0.75 m2,行人可用空间较小,行人速度选择受到限制,乘客之间有一定的影响,赶超其他行人受到限制,处于轻度拥挤状态。在9:22,9:24,9:29,9:42和10:07这5个时刻,客流突然增多,客流拥挤指数正确评价客流运行状态,为轻度拥挤,在4~6之间。
2) 基于VISSIM行人客流状态的仿真评价。
VISSIM是一款微观仿真工具。在VISSIM行人模块中,行人行为的仿真主要建立在社会力模型之上 。它是从社会力的角度、心理和物理上产生的影响共同构成对行人行为的推动力。这些影响行人行为的力可以是行人对目的的驱动力、周围行人对其的影响以及障碍物对其的干扰。在VISSIM中构建1:1的仿真模型,如图 3所示。

|
| 图 3 VISSIM构建地铁复兴门示意图 Fig. 3 Schematic diagram of construction of the Fuxingmen subway station using VISSIM |
VISSIM仿真软件可以建立地铁复兴门站仿真模型,构造出其轨道、通道、障碍、行人交通特性等因素,模拟其中行人的运行状态及其随时空变化的过程。通过对复兴门站进行实地考察与尺寸测量,如车辆间隔时间、行人路径和障碍物等方面。
通过采集地铁1号线上和地铁2号线站台某一区域由VISSIM生成的行人交通数据(采样周期为1min)得出2号线换乘1号线楼梯上的行人密度和行人流量。并可从中推算出行人流密度和平均单位宽度流率,以此作为输入,采用本文提出的客流运行状态模糊评价模型,通过MATLAB仿真获得了相应的客流拥挤指数。由于篇幅所限,在大量的实验数据中随机截取了40组仿真数据,如表 5所示。
| 时刻 | 客流数据 | 模糊评价结果 | 时刻 | 客流数据 | 模糊评价结果 | ||||||
| 平均 密度 | 单位宽 度人流 | 客流拥 挤指数 | 客流 状态 | 手册等 级对照 | 平均 密度 | 单位宽 度人流 | 客流拥 挤指数 | 客流 状态 | 手册等 级对照 | ||
| 1 | 1.27 | 41.90 | 5.00 | 轻度拥挤 | C | 21 | 2.60 | 53.80 | 6.00 | 中度拥挤 | D |
| 2 | 1.33 | 42.75 | 5.70 | 轻度拥挤 | C | 22 | 2.77 | 52.48 | 8.45 | 严重拥挤 | E |
| 3 | 1.35 | 42.01 | 5.65 | 轻度拥挤 | C | 23 | 2.84 | 49.31 | 8.40 | 严重拥挤 | E |
| 4 | 1.36 | 43.14 | 5.80 | 轻度拥挤 | C | 24 | 3.00 | 50.23 | 8.50 | 严重拥挤 | E |
| 5 | 1.41 | 43.85 | 5.80 | 轻度拥挤 | C | 25 | 3.09 | 47.28 | 8.60 | 严重拥挤 | E |
| 6 | 1.46 | 45.85 | 5.70 | 轻度拥挤 | C | 26 | 3.11 | 48.77 | 8.60 | 严重拥挤 | E |
| 7 | 1.48 | 44.37 | 5.85 | 轻度拥挤 | C | 27 | 3.16 | 47.99 | 8.70 | 严重拥挤 | E |
| 8 | 1.51 | 46.87 | 5.90 | 轻度拥挤 | C | 28 | 3.21 | 48.17 | 8.70 | 严重拥挤 | E |
| 9 | 1.53 | 47.37 | 5.90 | 轻度拥挤 | D | 29 | 3.28 | 44.82 | 8.80 | 严重拥挤 | E |
| 10 | 1.56 | 46.11 | 6.00 | 中度拥挤 | D | 30 | 3.33 | 47.03 | 8.90 | 严重拥挤 | E |
| 11 | 1.60 | 47.97 | 6.20 | 中度拥挤 | D | 31 | 3.38 | 43.63 | 8.90 | 严重拥挤 | E |
| 12 | 1.62 | 46.31 | 6.30 | 中度拥挤 | D | 32 | 3.40 | 45.34 | 8.90 | 严重拥挤 | E |
| 13 | 1.70 | 49.86 | 6.60 | 中度拥挤 | D | 33 | 3.45 | 41.30 | 9.00 | 严重拥挤 | E |
| 14 | 1.93 | 51.66 | 6.60 | 中度拥挤 | D | 34 | 3.50 | 42.79 | 8.95 | 严重拥挤 | E |
| 15 | 2.20 | 53.76 | 6.10 | 中度拥挤 | D | 35 | 3.60 | 36.97 | 9.10 | 严重拥挤 | E |
| 16 | 2.35 | 52.99 | 6.30 | 中度拥挤 | D | 36 | 3.66 | 34.51 | 9.10 | 严重拥挤 | E |
| 17 | 2.42 | 55.03 | 5.70 | 中度拥挤 | D | 37 | 3.70 | 30.99 | 9.20 | 严重拥挤 | E |
| 18 | 2.47 | 54.82 | 5.80 | 中度拥挤 | D | 38 | 3.74 | 28.52 | 9.30 | 严重拥挤 | E |
| 19 | 2.50 | 54.23 | 5.90 | 中度拥挤 | D | 39 | 3.80 | 26.06 | 9.30 | 严重拥挤 | E |
| 20 | 2.56 | 54.83 | 5.80 | 中度拥挤 | D | 40 | 3.82 | 23.94 | 9.15 | 严重拥挤 | E |
VISSIM行人仿真客流状态模糊评价结果如图 4所示。

|
| 图 4 VISSIM行人仿真客流状态模糊评价结果图 Fig. 4 Result of fuzzy evaluation of passenger flow state using VISSIM pedestrian simulation |
在仿真交通流数据和评价结果可以显示,11个连续中度拥挤状态,19个连续严重拥挤状态,有7个客流拥挤指数大于9的严重拥挤状态。实时发布的信息和动态诱导,使管理者有针对性地采取人员诱导和限流等措施,可以实现了对大客流进的预警组织,从而更好地解决乘客流拥挤问题;而乘客看到发布的枢纽客流状态信息,自觉规避拥挤和危险,保障乘客的出行安全。
以上结果与《运输能力与服务质量手册》评价等级一致。由此可以看出,客流在缓慢变化的时候能够准确评价,而且在客流变化较为剧烈时也能够准确地评价乘客流的运行状态。通过视频采集的行人区域内没有连续超过5个是拥挤状态,故其处于畅通、安全运行状态;而VISSIM仿真的行人区域内出现连续严重拥挤状态,故其应采取必要措施,缓解拥挤状态。
由此可以得出,客流拥挤指数较好地反映了枢纽内客流运行状态,评价结果与人的主观感受一致,符合《行人交通》楼梯处的服务水平。通过模糊推理得到的客流拥挤指数具有一定的客观性、科学性、稳定性和可信度,简洁明了的告知管理者和乘客枢纽内各服务设施的运行状态。同时,通过实时发布各服务设施的客流拥挤指数信息,能够使管理者和乘客提前预警,避免乘客流拥挤、紊乱的发生,消除乘客流拥挤带来的安全隐患,实现交通枢纽站内的安全、高效、便捷运行。
5 结束语本文基于综合模糊评价模型提出了枢纽内客流运行状态评价指标,并通过地铁枢纽内楼梯处运行状况进行了客流状态仿真评价分析与验证。文中所提出的客流拥挤指数客观地反映了枢纽内各服务设施的客流运行状态,其不仅可以从宏观上简单、明了地表明当前枢纽内各服务设施的状态—拥挤或者不拥挤,定量地表示出拥挤到何种程度,而且管理者和社会公众也可以通过客流拥挤指数掌握枢纽内各服务设施客流运行的拥挤程度、趋势和规律,便予诱导客流是否出行或以什么方式出行,为枢纽内管理部门及乘客提供有益参考。
| [1] | 王会会.综合客运交通枢纽内部客流拥堵机理研究[D]. 北京: 北京交通大学, 2011: 23-25. WANG Huihui. Passenger congestion mechanism analysis in comprehensive passenger transportation terminal [D]. Beijing: Beijing Jiaotong University, 2011: 23-25. |
| [2] | 房霄虹, 周磊山, 周勃. 基于可排序DEA的城市综合交通枢纽评价方法研究[J]. 交通运输系统工程与信息,2008, 8 (2) : 108 –113. FANG Xiaohong, ZHOU Leishan, ZHOU Bo. Evaluation method of city comprehensive transportation hub based on permutable DEA model[J]. Journal of Transportation Systems Engineering and Information Technoloy,2008, 8 (2) : 108 –113. |
| [3] | 马莉.城市轨道交通枢纽乘客交通流状态分析与评价[D]. 北京:北京交通大学,2009:15-25. MA Li. Analysis and evaluation of passenger flow operation state in urban railway transit hub[D]. Beijing: Beijing Jiaotong University, 2009: 15-25. |
| [4] | 於毅.城市道路交通状态判别方法研究[D]. 北京:北京交通大学, 2007: 15-17. YU Yi. Research on the identification method of urban road traffic conditions[D]. Beijing: Beijing Jiaotong University, 2007 : 15-17. |
| [5] | 杨兆升, 张茂雷. 基于模糊综合评判的道路交通状态分析模型[J]. 公路交通科技,2010, 27 (9) : 121 –126. YANG Zhaosheng, ZHANG Maolei. A model for road traffic state analys based on fuzzy comprehensive evaluation[J]. Journal of Highway and Transportation Research and Development,2010, 27 (9) : 121 –126. |
| [6] | 孙超.城市道路交通状态评价分析研究[D]. 广州:华南理工大学, 2010: 25-31. SUN Chao. Research on urban traffic network state evaluation and analysis[D]. Guangzhou: South China University of Technology, 2010: 25-31. |
| [7] | 陈艳艳, 李平普, 张广厚, 等. 综合交通枢纽客流拥挤实时评价方法[J]. 公路交通科技,2012, 29 : 75 –80. CHEN Yanyan, LI Pingpu, ZHANG Guanghou, et al. Real-ime evaluation method of passenger crowding in integrated transport hub[J]. Journal of Highway and Transportation Research and Development,2012, 29 : 75 –80. |



