2. 中国科学院大学, 北京 100049
2. University of the Chinese Academy of Sciences, Beijing 100049, China
输电线巡检机器人研究始于20世纪80年代,近年来成为机器人领域的研究热点[1-5]。轮臂复合结构的输电线巡检机器人是当前巡检机器人中的常见类型,这种机器人通过轮臂复合机构实现机器人在架空输电线上行走及跨越线路障碍。机器人在跨越障碍时需要在单臂挂线状态下调节各关节运动使脱线手臂跨越障碍物。机器人跨越障碍时的姿态变化使得机器人的质量分布发生变化,从而造成倾斜,导致机器人承受附加倾覆力矩而处于不稳定状态,尽管挂线手臂通过夹线机构能够提供一定的夹紧力,但是过大的夹紧力容易损坏挂线处的输电线路。由于机械结构限制,机器人倾斜还容易使脱线手臂与线路发生干涉。因此保持机器人越障时处于动态稳定状态是实现机器人越障的关键。机器人的动态稳定状态是指在机器人单臂挂线运动时通过实时调整机器人质心位置而保持机器人处于水平姿态的状态。文献[6]中通过模型计算,规划配重块的位置以调整机器人质心实现机器人的稳定运动,这种方法对建模精度要求很高;文献[7]提出一种通过控制配重块位置调整质心的方法,利用静力矩平衡方程初步估计配重块位置,当配重块到达估计位置后再利用倾角传感器的输出调整配重块位置使机器人稳定在水平姿态,这种方法可以保证机器人最终在稳定状态,但是无法保证运动过程中机器人始终处于稳定状态,即无法保证机器人质心的动态稳定。本文针对一种双臂巡检机器人越障过程中的动态稳定问题,提出一种质心调整策略。分析了机器人越障过程中的动力学模型,以过渡时间最短为目标规划机器人的关节运动轨迹。为了确认机器人是否水平,在机器人箱体位置安装了倾角传感器,实时反馈机器人倾角。根据机器人倾角设计了状态反馈H∞控制器,利用机器人倾角和关节位移实时调节各关节运动,通过控制调整机器人质心位置实现机器人越障时的稳定运动。
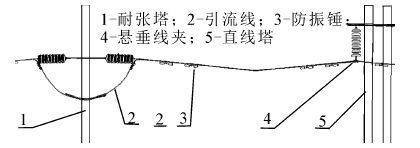
1 巡检机器人及其越障过程 1.1 巡检机器人结构巡检机器人沿输电导线行走,并携带检测设备对输电导线进行检测,输电导线的障碍物环境如图 1所示。巡检机器人沿输电导线以滚动的方式运动,遇到安装在导线上的防振锤、线夹和引流线等障碍物时,机器人采取尺蠖或双臂交错的方式跨越障碍物。
|
| 图 1 输电线的障碍物环境 Fig. 1 Obstacle environment on power transmission line |
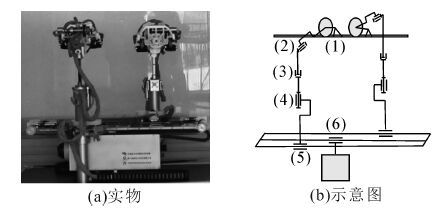
巡检机器人由行走越障机构、质心调整机构和控制箱体组成,图 2所示。机器人行走越障机构由两个轮-爪-臂复合手臂组成,每个手臂分别有行走关节(图 2(1))、腕关节(图 2(2))、伸缩关节(图 2(3))和旋转关节(图 2(4)),手臂末端安装夹爪,可以抓握导线。机器人质心调节机构由双臂导轨和控制箱导轨组成,分别由3个移动关节驱动(图 2(5)和图 2(6)),可以实现两臂和控制箱沿导轨水平运动;控制箱体装有机器人控制系统及电源等,同时具有机器人质心配重块的作用。
|
| 图 2 巡检机器人结构 Fig. 2 Structure of the robot |
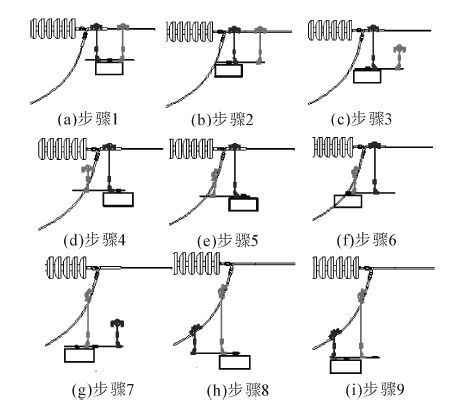
机器人以双臂交错方式跨越障碍物或通过引流线时,经常需要在单臂挂线状态下调节各关节运动。以跨越耐张线夹为例,越障流程如图 3所示。
|
| 图 3 巡检机器人越障流程(耐张线夹) Fig. 3 The obstacle negotiating process of the robot |
1) 机器人正常在架空导线上行使时,其质心在两臂中间,两臂间距为Δ;
2) 当机器人遇到线夹后,停止运动,移动双臂和控制箱在导轨上的位置,将机器人质心调整至前臂下;
3) 后臂伸长脱线,并旋转90°以避让导线,后臂收缩或前臂伸长使后臂轮爪降至线下;
4) 保持机器人在水平状态,驱动双臂导轨和控制箱的移动关节使两臂间距由Δ调整至-Δ;
5) 后臂抬高至线上并回转-90°;
6) 后臂收缩落线,调整质心至后臂;
7)-8) 前臂依同样方式跨越线夹;
9) 前臂落线完成后调整质心至两臂中间,完成双臂交错跨越。
分析上述越障过程,机器人质心调整主要发生在以下3种情况:
1) 机器人双臂挂线,通过改变机器人手臂和控制箱在导轨上的位置使质心在两臂中间、前臂下、后臂下之间相互转换,如过程(b)、(f)、(i);
2) 机器人单臂挂线,保持稳定状态(即机器人在水平姿态)将两臂间距由Δ变化至Δnew,如过程(d);
3) 机器人单臂挂线,手臂伸缩或旋转时保持机器人在稳定状态,如过程(c)、(e)、(f)。
这3种情况以第2种最为复杂和关键,整个过程中应保持机器人在动态稳定状态。当机器人在运动中产生倾斜时,抓线手臂对输电线俯仰方向的作用力将对输电线产生危害。机器人倾斜影响脱线手臂与输电线的相对关系,同时影响机器人的力学特性,使得机器人处于不安全状态。因此,保持机器人在稳定状态是机器人越障的关键。
本文以机器人后臂挂线,保持机器人处于稳定状态调整两臂间距由Δ至Δnew为研究对象,通过调节双臂导轨和控制箱移动关节的运动控制机器人质心位置,从而保证机器人在运行过程中始终在稳定状态。
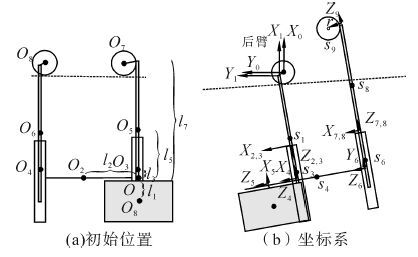
2 机器人单臂挂线的动力学模型机器人单臂挂线运动时,一只手臂悬挂在输电线上,通过悬挂手臂的夹爪将机器人的行走轮固定在输电线上,另一手臂在空间运动。以后臂挂线运动为例,忽略输电线振动和变形对机器人的影响,在后臂悬挂点中心建立基坐标X0Y0Z0,假设该基坐标固定。机器人有9个运动关节,设mi(i=0,1,...,9) 为各连杆的质量,si为各连杆的质心在本连杆坐标系中的位置,li为机器人在初始位置时各质心之间的连接长度,如图 4(a)所示。θ为机器人水平倾斜角度,D为导轨总长。在此基础上,建立机器人各连杆的D-H坐标系,如图 4(b)所示。
|
| 图 4 机器人初始位置及坐标系 Fig. 4 Coordinates of the robot |
采用牛顿-欧拉迭代算法建立机器人的动力学模型,各连杆的速度和加速度迭代方程表示为
若关节i+1为转动关节
| $\left\{ {\begin{array}{*{20}{l}} {^{i + 1}{\omega _{i + 1}} = {}_i^{i + 1}{R^i}{\omega _i} + {{\dot \theta }_{i + 1}}^{i + 1}{Z_{i + 1}}}\\ {^{i + 1}{{\dot \omega }_{i + 1}} = {}_i^{i + 1}{R^i}{{\dot \omega }_i} + {}_i^{i + 1}{{\dot R}^i}{\omega _i} \times {{\dot \theta }_{i + 1}}^{i + 1}{{\hat Z}_{i + 1}} + {{\ddot \theta }_{i + 1}}^{i + 1}{{\hat Z}_{i + 1}}}\\ {^{i + 1}{{\dot \upsilon }_{i + 1}} = {}_i^{i + 1}R\left( {^i{{\dot \omega }_i} \times {}^i{P_{i + 1}}{ + ^i}{\omega _i} \times \left( {^i{\omega _i} \times {}^i{P_{i + 1}}} \right){ + ^i}{{\dot \upsilon }_i}} \right)}\\ {^{i + 1}{F_{i + 1}} = {m_{i + 1}}\left( {^{i + 1}{{\dot \omega }_{i + 1}} \times {s_{i + 1}}{ + ^{i + 1}}{\omega _{i + 1}} \times \left( {^{i + 1}{\omega _{i + 1}} \times {s_{i + 1}}} \right){ + ^{i + 1}}{{\dot \upsilon }_{i + 1}}} \right)}\\ {^{i + 1}{N_{i + 1}} = {I_{i + 1}}^{i + 1}{{\dot \omega }_{i + 1}}{ + ^{i + 1}}{\omega _{i + 1}} \times {I_{i + 1}}^{i + 1}{\omega _{i + 1}}} \end{array}} \right.$ | (1) |
若关节i+1为移动关节
| ${\begin{array}{*{20}{l}} {^{i + 1}{\omega _{i + 1}} = {}_i^{i + 1}{R^i}{\omega _i}}\\ {^{i + 1}{{\dot \omega }_{i + 1}} = {}_i^{i + 1}{R^i}{{\dot \omega }_i}}\\ \begin{array}{l} ^{i + 1}{{\dot v}_{i + 1}} = {}_i^{i + 1}R\left( {^i{{\dot \omega }_i} \times {}^i{P_{i + 1}}{ + ^i}{\omega _i} \times \left( {^i{\omega _i} \times {}^i{P_{i + 1}}} \right){ + ^i}{{\dot v}_i}} \right) + \\ {2^{i + 1}}{\omega _{i + 1}} \times {{\dot d}_{i + 1}}^{i + 1}{{\hat Z}_{i + 1}} + {{\ddot d}_{i + 1}}^{i + 1}{{\hat Z}_{i + 1}} \end{array}\\ {^{i + 1}{F_{i + 1}} = {m_{i + 1}}\left( {^{i + 1}{{\dot \omega }_{i + 1}} \times {s_{i + 1}}{ + ^{i + 1}}{\omega _{i + 1}} \times \left( {^{i + 1}{\omega _{i + 1}} \times {s_{i + 1}}} \right){ + ^{i + 1}}{{\dot v}_{i + 1}}} \right)}\\ {^{i + 1}{N_{i + 1}} = {I_{i + 1}}^{i + 1}{{\dot \omega }_{i + 1}}{ + ^{i + 1}}{\omega _{i + 1}} \times {I_{i + 1}}^{i + 1}{\omega _{i + 1}}} \end{array}}$ | (2) |
式中:i+1iR表示坐标系i在坐标系i+1中的旋转变化关系,iPi+1为坐标系i+1在坐标系i中的平移变化关系,iωi、$^i{{\dot \omega }_i}$、ivi和$^i{{\dot v}_i}$表示连杆i的角速度、角加速度、线速度和线加速度矢量,iFi和iNi表示连杆i质心处所受的惯性力和惯性力矩,θi和di表示关节i的关节变量,Ii表示连杆i的惯性矩阵。
忽略各关节之间的摩擦力,则作用在关节i的力和力矩由下列迭代算法给出:
| $\left\{ {\begin{array}{*{20}{l}} {^i{f_i} = {}_{i + 1}^i{R^{i + 1}}{f_{i + 1}}{ + ^i}{F_i}}\\ {^i{{\dot n}_i}{ = ^i}{N_i} + {}_{i + 1}^i{R^{i + 1}}{n_{i + 1}} + {s_i}{ \times ^i}{F_i} + {}^i{P_{i + 1}} \times {}_{i + 1}^i{R^{i + 1}}{f_{i + 1}}} \end{array}} \right.$ | (3) |
机器人在后臂挂线状态下运动时,后臂腕关节(关节1) 电机处于自由状态。由式(1)~(3) 求的施加在关节1处的力矩为
| ${\tau _1} = {}^1{{\hat Z}_1}{}^1{n_1}$ | (4) |
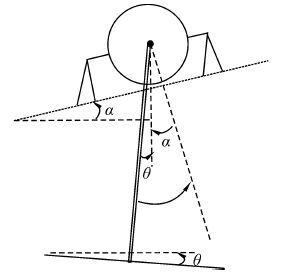
式中:τ1由后臂俯仰关节被动机构提供的阻尼决定。阻尼所提供的力矩与后臂俯仰角度θ-α成反比,其中α为输电导线与水平面的夹角,k为阻尼系数,如图 5所示。则
| ${\tau _1} = - k\left( {\theta - \alpha } \right)$ | (5) |
|
| 图 5 后臂悬挂的几何关系 Fig. 5 Geometrical relationship |
由(1)~(5) 得机器人绕关节1的z轴的力矩平衡方程为
| $ - k\left( {\theta - \alpha } \right) = {}^1{{\hat Z}_1}{}^1{n_1}$ | (6) |
机器人后臂挂线,调整两臂间距时,一般只需调节关节4、关节5和关节6位置,关节1被动适应,其他关节保持不变,即d2=d20,θ3=θ30,θ7=θ70,d8=d80,θ9=θ90。机器人在运动过程中,倾斜角度θ一般不会过大,设-10°≤θ≤10°,故可近似cos θ≈1,sin θ≈θ,将(6) 整理得:
| $J\ddot \theta - \left( {{g_u} + k} \right)\theta = {f_1}\ddot u + {f_2}u + {f_3}$ | (7) |
式中:
| $\begin{array}{*{20}{c}} {J = \sum {\left( {{m_i}{{\left| {{}^0{s_i}} \right|}^2} + {I_i}} \right)} }\\ {{g_u} = g\left[ { - \begin{array}{*{20}{c}} {{m_5}}&{{m_6}}&{{m_3}}&{{m_8}}&{{m_1}}&{{m_9}} \end{array}} \right] \cdot }\\ {{{\left[ {\begin{array}{*{20}{c}} {{l_1}}&{{l_3}}&{{l_4}}&{{l_5}}&{{l_6}}&{{l_7}} \end{array}} \right]}^{\rm{T}}} + g\left[ {\begin{array}{*{20}{c}} {{m_{89}}}&{{m_1}} \end{array}} \right]{{\left[ {\begin{array}{*{20}{c}} {{d_8}}&{{d_2}} \end{array}} \right]}^{\rm{T}}}}\\ {{f_1} = \left[ {\begin{array}{*{20}{c}} {{m_5}{l_{17}}}&{{m_{6789}}{l_{17}}}&{{m_{456789}}{l_{17}}} \end{array}} \right]}\\ {{f_2} = \left[ {\begin{array}{*{20}{c}} {{m_5}}&{{m_{6789}}}&{{m_{456789}}} \end{array}} \right]}\\ {{f_3} = {m_3}g{l_2} - D{m_{46789}}g - {m_9}grs{\theta _7} + k\alpha }\\ {u = {{\left[ {\begin{array}{*{20}{c}} {{d_5}}&{{d_4}}&{{d_6}} \end{array}} \right]}^{\rm{T}}}} \end{array}$ |
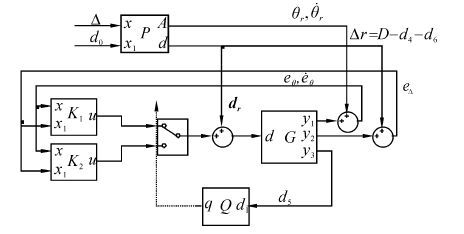
设计质心调整控制器结构如图 6所示。
|
| 图 6 质心调整控制器结构 Fig. 6 Framework of centroid adjustment controller |
在质心调整过程中,如控制箱体(d5)可调,由控制器Kc1调节,通过实时调节d5保持机器人平稳,并通过协调d4、d6使两臂间距Δ按规划运动;当控制箱体d5不可调时切换至控制器Kc2,通过协调两臂运动(d4,d6)保持机器人平稳,且使两臂间距Δ按规划运动。控制器切换由Q触发,P为规划器。
| $Q = \left\{ {\begin{array}{*{20}{l}} {{K_{c1}},0 < {d_5} < {d_{5\max }}}\\ {{K_{c2}},其他} \end{array}} \right.$ | (8) |
机器人静止时,满足静力矩平衡方程:
| $ - k\left( {\theta - \alpha } \right) - \sum {{m_i}g\left( {{}^0{s_i}{}^0{{\hat Y}_0}} \right)} = 0$ | (9) |
整理得:
| $\begin{array}{l} {m_5}g\left( {c\theta c{\theta _3}\left( {{d_4} - {d_5}} \right) + rc\theta s{\theta _3} - s\theta \left( {{l_1} + {d_2} + {l_7}} \right)} \right) + \\ {m_4}g\left( {c\theta c{\theta _3}\left( {{l_2} + {d_4} - D} \right) + rc\theta s{\theta _3} - s\theta \left( {{d_2} + {l_7}} \right)} \right) + \\ {m_6}g\left( {c\theta c{\theta _3}\left( {{d_6} + {d_4} - D} \right) + 2rc\theta s{\theta _3} + s\theta \left( {{l_3} - {d_2} - {l_7}} \right)} \right) + \\ {m_3}gs\theta \left( {{l_3} - {d_2} - {d_8}} \right) + {m_1}gs\theta \left( {{l_5} - {l_7}} \right) + {m_8}g\\ \left( {c\theta c{\theta _3}\left( {{d_6} + {d_4} - D} \right) + 2rc\theta s{\theta _3} - s\theta \left( {{l_7} - {l_5} - {d_8} + {d_2}} \right)} \right) + \\ {m_9}g\left( {c\theta c{\theta _3}\left( {{d_6} + {d_4} - D} \right) + 2rc\theta s{\theta _3} + s\theta \left( {{d_8} - } \right.} \right.\\ \left. {{d_2}} \right) - rc\theta c{\theta _3}s{\theta _7} - rc\theta s{\theta _3}c{\theta _7} = - k\left( {\theta - \alpha } \right) \end{array}$ |
以巡检机器人后臂悬挂在输电线上,保持机器人在稳定状态调整两臂间距由Δ0至Δ为研究对象。机器人通过双臂导轨和控制箱移动关节相互配合实现由初始位置θ10,d20,θ30,d40,d50,d60,θ70,d80,θ90保持θ=0调整两臂间距至Δ。关节变量的期望值为θ1,d2,θ3,d4,d5,d6,θ7,d8,θ9,调整过程中保持d2=d20,θ3=θ30,θ7=θ70,d8=d80,θ9=θ90。关节变量的期望值满足式(9),整理得:
| $\left\{ {\begin{array}{*{20}{l}} {a_1^0d_5^0 + a_2^0d_6^0 + a_3^0d_4^0 = {b^0}\left( {{\theta ^0}} \right)}\\ {a_1^0{d_5} + a_2^0{d_6} + a_3^0{d_4} = {b^0}\left( {{\theta ^0}} \right)} \end{array}} \right.$ | (10) |
式中:a10,a20,d30,b0(θ0)和b0(θ)是与机器人参数、关节变量初始值θ10,d20,θ30,d40,d50,d60,θ70,d80,θ90以及θ、θ0和α有关的参数。
由于机器人3个水平移动关节最大速度相同,则机器人调整时间最短即3个水平移动关节的最大位移最小。3个水平移动关节的期望值d5,d4,d6应满足:
| $\left\{ {\begin{array}{*{20}{l}} {a_1^0\left( {{d_5} - d_5^0} \right) + a_2^0\left( {{d_6} - d_6^0} \right) + a_3^0\left( {{d_4} - d_4^0} \right) = }\\ {{b^0}\left( \theta \right) - {b^0}\left( {{\theta ^0}} \right)}\\ {{d_6} - d_6^0 + {d_4} - d_4^0 = {\Delta _0} - \Delta }\\ {0 \le {d_4},{d_5},{d_6} \le d}\\ {\min \left( {\max \left( {\left| {{d_4} - d_4^0} \right|,\left| {{d_5} - d_5^0} \right|,\left| {{d_6} - d_6^0} \right|} \right)} \right)} \end{array}} \right.$ | (11) |
采取遍历变量的方法解式(11) 得满足调整时间最短的机器人期望关节变量。
3.2 d5可调,设计控制器Kc1令d=dr-Δd,则eΔ=Δr-Δ=-Δd6-Δd4 。代入式(7) 得
| ${J_t}\ddot \theta = \left( {{g_u} + k} \right)\theta - {m_5}g\Delta {d_5} + h$ |
其中:$h = {f_2}{u_r} + {f_1}\ddot u + {f_3} + {m_{6789}}g{e_\Delta } - {m_{45}}g\Delta {d_4}$
令e=θr-θ,则
| $ - {J_t}\ddot e = - {g_u}e - {m_1}g\Delta {d_5} + h - {J_t}{\theta _r} + {g_u}{\theta _r}$ | (12) |
将式(12) 转化为
| $\begin{array}{*{20}{l}} {\dot x = Ax + {B_2}u + {B_1}w}\\ {z = Cx + {D_2}u + {D_1}w} \end{array}$ |
式中:$\begin{array}{l} x = {\left[ {\begin{array}{*{20}{l}} e&{\dot e} \end{array}} \right]^{\rm{T}}},u = {\left[ {\begin{array}{*{20}{l}} {\Delta {d_5}}&{\Delta {d_6}} \end{array}} \right]^{\rm{T}}},A = \left[ {\begin{array}{*{20}{c}} 0&1\\ {\frac{{{g_u}}}{{{J_t}}}}&0 \end{array}} \right],\\ {B_2} = \left[ {\begin{array}{*{20}{c}} 0\\ {\frac{{{m_1}g}}{{{J_t}}}} \end{array}} \right],{B_1} = \left[ {\begin{array}{*{20}{c}} 0\\ 1 \end{array}} \right],C = \left[ {\begin{array}{*{20}{c}} 1&0 \end{array}} \right],{D_1} = {D_2} = 0,\\ w = h - {J_t}{\theta _r} + {g_u}{\theta _r} \end{array}$。
设计H∞最优状态反馈控制器u=W(X)-1x[8-9],即$\Delta {d_1} = \left[ {\begin{array}{*{20}{c}} {{k_{11}}}&{{k_{12}}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} e\\ {\dot e} \end{array}} \right]$。又Δd4=-eΔ-Δd6,得
| $\left[ {\begin{array}{*{20}{c}} {\Delta {d_5}}\\ {\Delta {d_6}}\\ {\Delta {d_4}} \end{array}} \right] = {K_{c1}}\left[ {\begin{array}{*{20}{c}} e\\ {\dot e}\\ {{e_\Delta }} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {{k_{11}}}&{{k_{12}}}&0\\ 0&0&{ - 1/2}\\ 0&0&{ - 1/2} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} e\\ {\dot e}\\ {{e_\Delta }} \end{array}} \right]$ |
将eΔ=-Δd6-Δd4 。代入式(7) 得
| ${J_t}\ddot \theta = \left( {{g_u} + k} \right)\theta - \left( {{m_{6789}}} \right){m_{456789}}g\Delta {d_6} + h$ |
式中:$h = {f_2}{u_r} + {f_1}\ddot u + {f_3} + {m_{6789}}g{e_\Delta } - {m_5}g\Delta {d_5}$
设计H∞最优状态反馈控制器u=W(X)-1x,即$\Delta {d_3} = \left[ {\begin{array}{*{20}{c}} {{k_{21}}}&{{k_{22}}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} e\\ {\dot e} \end{array}} \right]$。又$\Delta {d_4} = - {e_\Delta } - \Delta {d_6} = - {e_\Delta } - {k_{21}}e - {k_{22}}\dot e$,得
| $\left[ {\begin{array}{*{20}{c}} {\Delta {d_5}}\\ {\Delta {d_6}}\\ {\Delta {d_4}} \end{array}} \right] = {K_{c2}}\left[ {\begin{array}{*{20}{c}} e\\ {\dot e}\\ {{e_\Delta }} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} 0&0&0\\ {{k_{21}}}&{{k_{22}}}&0\\ { - {k_{21}}}&{ - {k_{22}}}&{ - 1} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} e\\ {\dot e}\\ {{e_\Delta }} \end{array}} \right]$ |
仿真中使用的巡检机器人模型参数为:D=0.78,J≈1,gu=-19.168,f1=[1.02 0.6 -2.04],f2=[17 10.01 34.01],f3=-24。由于建模误差的存在,实际机器人参数与模型存在偏差,假设实际机器人参数为:f1=[1.2 0.66 -2.1],f2=[20 11 35],其他参数相同。设计控制器:
| $\begin{array}{l} {K_{c1}} = \left[ {\begin{array}{*{20}{c}} {1.6412}&{ - 0.1669}&0\\ 0&0&{ - 1/2}\\ 0&0&{ - 1/2} \end{array}} \right]\\ {K_{c2}} = \left[ {\begin{array}{*{20}{c}} 0&0&0\\ { - 1.2832}&{ - 0.1236}&0\\ {1.2832}&{0.1236}&{ - 1} \end{array}} \right] \end{array}$ |
机器人的初始条件为初始位置$\begin{array}{l} \left[ {\begin{array}{*{20}{c}} {\theta _1^0}&{d_2^0}&{\theta _3^0}&{d_4^0}&{d_5^0}&{d_6^0}&{\theta _7^0}&{d_8^0}&{\theta _9^0} \end{array}} \right] = \\ \left[ {\begin{array}{*{20}{c}} 0&0&0&{0.36}&{0.5036}&{0.32}&0&{0.2}&0 \end{array}} \right] \end{array}$两臂间距Δ0=0.1,初始偏角θ0=0.098。调整后机器人状态为两臂间距Δ=0.3,偏角θ=0。解规划器P,即机器人期望位置:$\begin{array}{l} \left[ {\begin{array}{*{20}{c}} {\theta _1^0}&{d_2^0}&{\theta _3^0}&{d_4^0}&{d_5^0}&{d_6^0}&{\theta _7^0}&{d_8^0}&{\theta _9^0} \end{array}} \right] = \\ \left[ {\begin{array}{*{20}{c}} 0&0&0&{0.2605}&{0.5266}&{0.21}&0&{0.2}&0 \end{array}} \right] \end{array}$两臂间距Δ=0.3,偏角θ=0。
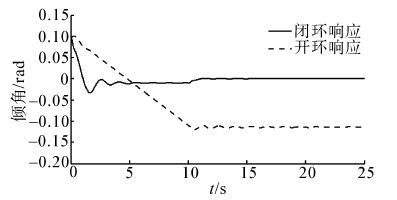
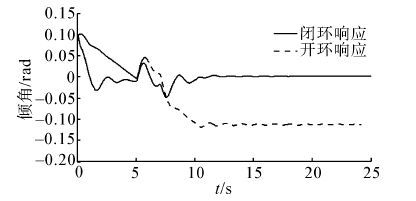
图 7是存在建模误差情况下,机器人的开环和闭环响应曲线。结果表明所设计的控制器可以保证机器人系统的稳定性,能在建模误差存在的情况下,将机器人倾角偏差调节到能够接受的范围内,从而保证了机器人在调整质心过程中保持稳定状态。图 8是在运动过程中,机器人同时受到风载外力矩干扰和关节速度响应干扰时,机器人的响应曲线对比,结果表明控制器能抑制干扰对倾角的影响,使机器人平稳并保持两臂间距按规划值变化。其中虚线为不加控制作用时的开环响应曲线,实线为有控制作用时的闭环响应曲线。
|
| 图 7 机器人倾角的开环和闭环响应 Fig. 7 Open and closed loop response of the robot |
|
| 图 8 加入干扰后倾角的开环和闭环响应 Fig. 8 Open and closed loop response of the robot with disturbances |
在实验室模拟的输电线路上进行巡检机器人质心调节实验,如图 9所示。实验内容为:后臂行走轮落在导线上,前臂抬起,将两臂间距由300 mm调整至-300 m,机器人初始的倾角为-5.2°,机器人倾角的开环和闭环响应曲线如图 10所示。实验表明在两臂间距调整过程中机器人两手臂和控制箱沿导轨协调运动,机器人倾角稳定在设定值0°。

|
| 图 9 质心调节实验 Fig. 9 Centroid adjustment experiment |

|
| 图 10 试验中机器人倾角的开环和闭环响应 Fig. 10 Open and closed loop response of the robot in experiment |
巡检机器人单臂悬挂运动是实现机器人越障的关键环节,针对巡检机器人单臂悬挂运动时的机器人的动态稳定问题,本文提出了一种能够实时保持机器人在稳定状态的质心调整策略。实验表明所提出的策略能够在存在建模误差和干扰的情况下,使机器人在双臂交错运动时保持稳定状态。本文在研究过程中忽略了输电导线柔性特性的影响,将机器人挂线手臂的行走轮固定在了刚性导线上。在实际中,受导线柔性的影响,机器人和导线构成了一个强耦合的动力学系统[12]。特别是在机器人通过引流线时,大垂度引流线的振动和变形对机器人质心调整有很大影响,该问题还在进一步研究中。
| [1] | KATRASNIK J, PERNUS F, LIKAR B. A survey of mobile robots for distribution power line inspection[J]. IEEE Transactions on Power Delivery,2010, 25 (1) : 485 –493. |
| [2] | POULIOT N, RICHARD P L, MONTAMBAULT S. LineScout power line robot: Characterization of a UTM-30LX LIDAR system for obstacle detection[C]//Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems. Vilamoura, Algarve, Portugal, 2012: 4327-4334. |
| [3] | HIGUCHI M, MAEDA Y, TSUTANI S, et al. Development of a mobile inspection robot for power transmission lines[J]. Journal of the Robotics Society of Japan,1991, 9 (4) : 457 –463. |
| [4] | MARIO F M C, ALEXANDRE Q B, GUILHERME A S P, et al. A mobile manipulator for installation and removal of aircraft warning spheres on aerial power transmission lines[C]//Proceedings of the IEEE International Conference on Robotics and Automation. Piscataway, USA: 2002: 3559-3564. |
| [5] | WANG H, ZHANG F, JIANG Y, et al. Development of an inspection robot for 500 kV EHV power transmission lines[C]//Proceedings of the 2010 IEEE/RSJ International Conference on Intelligent Robots and Systems. Taipei, China, 2010: 5107-5112. |
| [6] | 邬大为, 阮毅, 任志斌. 基于产生式系统和轨迹优化的巡线机器人控制[J]. 计算机工程与设计,2008, 29 (11) : 2868 –2870. WU Dawei, RUAN Yi, REN Zhibin. Inspection robot control system of power transmission line based on production system and trajectory optimization[J]. Computer Engineering and Design,2008, 29 (11) : 2868 –2870. |
| [7] | 朱兴龙, 王洪光, 房立金, 等. 自主越障巡检机器人质心调节控制[J]. 机器人,2006, 28 (4) : 385 –388. ZHU Xinglong, WANG Hongguang, FANG Lijin, et al. Centroid adjustment control on autonomous obstacle negotiating inspection robot[J]. Robot,2006, 28 (4) : 385 –388. |
| [8] | 喻向阳, 送鹏云, 张长胜. 状态反馈H∞控制器设计的线性矩阵不等式方法[J]. 昆明理工大学学报:理工版,2006, 31 (2) : 82 –85. YU Xiangyang, SONG Pengyun, ZHANG Changsheng. State feedback H∞ controller design via LM I approach[J]. Journal of Kunming University of Science and Technology: Science and Technology,2006, 31 (2) : 82 –85. |
| [9] | 周景雷. 机器人系统中的状态反馈控制器设计[J]. 菏泽学院学报,2009, 31 (5) : 52 –57. ZHOU Jinglei. State feedback control design in robotic systems[J]. Journal of Heze University,2009, 31 (5) : 52 –57. |
| [10] | 房立金. 架空线移动机器人主被动混合控制[J]. 华中科技大学学报: 自然科学版,2011, 39 . FANG Lijin. A passive-active hybrid control of wire-suspended mobile robot[J]. Journal of Huazhong University of Science and Technology: Natural Science Edition,2011, 39 . |
| [11] | 郭伟斌, 王洪光, 姜勇, 等. 一种输电线巡检机器人的自主抓线视觉伺服控制[J]. 机器人,2012, 34 (5) : 620 –627. GUO Weibin, WANG Hongguang, JIANG Yong, et al. Visual servo control for automatic line-grasping of a power transmission line inspection robot[J]. Robot,2012, 34 (5) : 620 –627. |
| [12] | 张廷羽, 张国贤, 金健, 等. 高压线巡检机器人动力学建模及分析[J]. 系统仿真学报,2008, 20 (18) : 4982 –4986. ZHANG Tingyu, ZHANG Guoxian, JIN Jian, et al. Dynamics modeling and analysis for power lines inspection robot[J]. Journal of System Simulation,2008, 20 (18) : 4982 –4986. |



