2. Department of Computer Science and Engineering, University at Buffalo
随着电子商务近年来突飞猛进的发展,物流配送逐渐成为电子商务的核心要素。由于需要协调与调度的资源数量和种类众多,给仓储物流中心的运作管理带来了前所未有的挑战。根据相关调查,传统模式的仓库中工人有60%~70%的时间都耗费在取货上[1]。在当前的电子商务中,物流配送具有发货单位小型化的特点,品种多、批量小、批次多、周期短,传统的人工操作、传送带式亦或AGV式的仓储物流方式已经难以适应电子商务的发展需求,以亚马逊的Kiva Systems为代表的基于移动机器人的自动化仓储正在兴起。
将自主移动机器人引入仓储空间中,代替人工搬运货物,可以有效地减少工人的劳动强度,降低维护成本,提高运行效率,并且对仓储空间的布局具有良好的可重构性。移动机器人在仓储空间中的定位,可以通过二维码、RFID、室内GPS等技术来解决。移动机器人集群与中心控制系统之间的通信,可以通过无线网络实现。在此基础上,要实现一个机器人化的自动化仓储环境,机器人集群需要解决的关键问题主要有:1) 在订单任务到达之后,移动机器人的智能调度;2) 在移动机器人集群运行的仓储环境中,机器人移动路径的规划和碰撞的预测、检测、防止;3) 在给定仓储空间和订单任务密度后,机器人配置数量的优化。
1 仓储空间结构和物流任务分析建立一个机器人化的自动化仓储空间的模型如图 1所示。主要考虑停放位置(空闲或货架占用)、入货口、出货口、纵向道路和横向道路。每个被2条纵向道路和2条横向道路围起来的区域内,有2排停放位置。
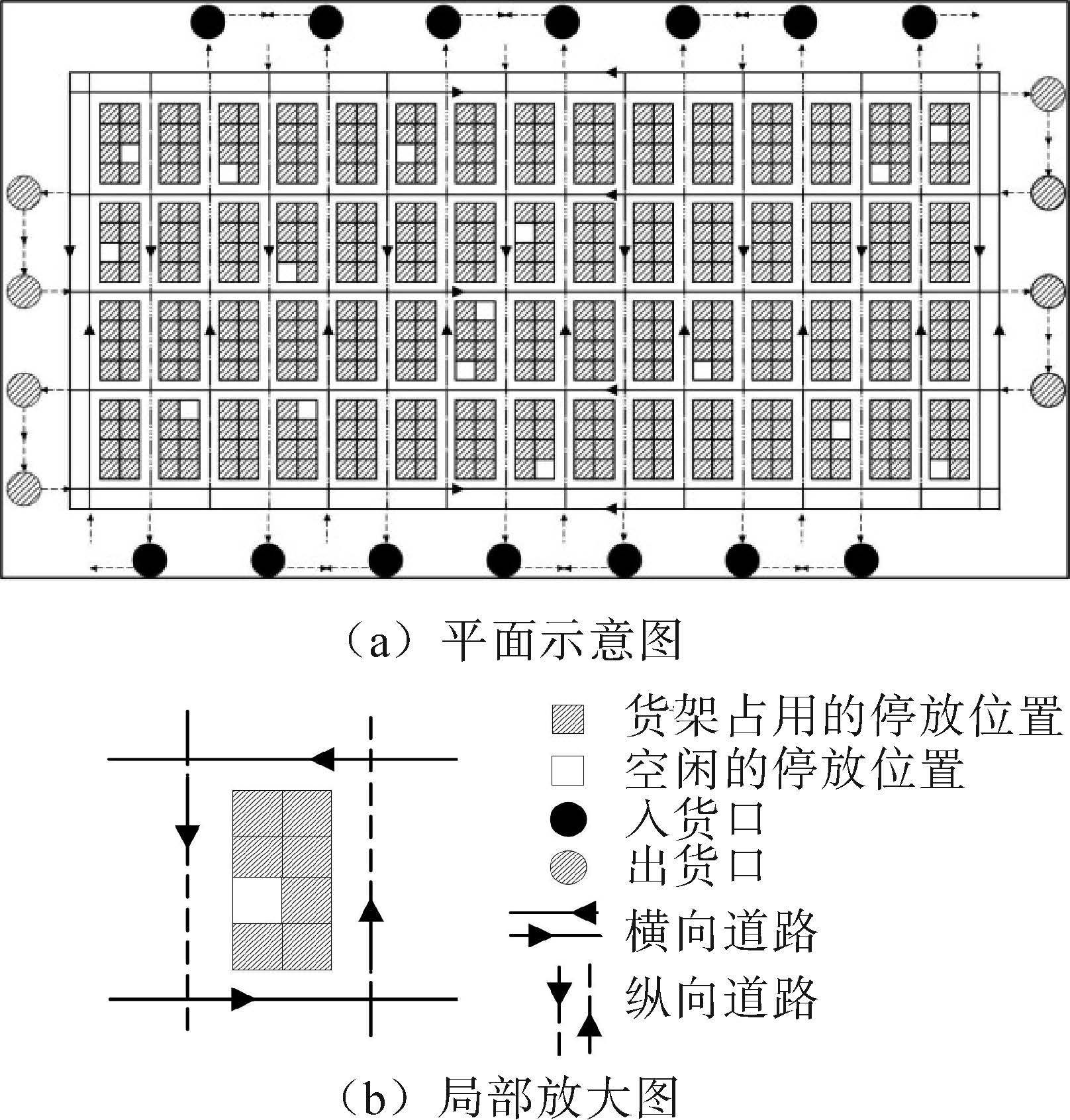
|
| 图 1 仓储空间全局平面示意图 Fig. 1 Warehouse floor plan overview |
这个仓储模型具有良好的可重构性,仓储空间的长度宽度、货架和道路的数量和密度、入货口出货口的数量和位置、订单的数量和密度等参数,都可以根据具体需要灵活设定。
在此仓储空间中,多个移动机器人同时运行,为了避免碰撞冲突、简化机器人的运行规则、提高系统安全运行的鲁棒性,设定货架区域间的横向、纵向道路均为单行道。
对于建立的仓储空间模型,物流任务的形式是运送某一货架从停放位置n1到某个入货口/出货口位置n2,待入货/出货任务完成后,再搬运回货架区域位置n3,如图 2所示。
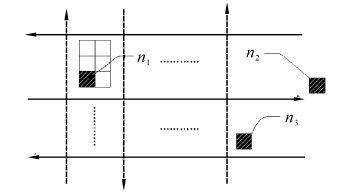
|
| 图 2 任务形式 Fig. 2 Task form |
物流任务可以分解成如图 3所示的3个步骤。其中,第1个和第3个步骤可以通过任务的分配调度进行优化,减少所花费的时间;第2个步骤可以采用路径规划方法对机器人的路径进行优化。

|
| 图 3 一个任务的流程图 Fig. 3 Task flow chart |
针对前述物流任务的第1个步骤进行优化,应使承担任务的机器人能尽早地运行到对应货架处。因此根据一个评价函数对所有可能执行任务的机器人进行评价,从中选取最合适的机器人[2]。
总的评价函数为
| ${g_n} = w \times {t_{{n_1}}} + {t_{{n_2}}}$ | (1) |
式(1) 表示第n个机器人执行此任务的总代价,tn1表示第n个机器人完成当前正在运行的任务预计要耗费的时间(若当前为空闲状态则此项为0)。w表示拥塞系数,用来反映系统的拥塞程度。设置w>1可以反映完成当前任务耗费的实际时间要多于预计的时间。tn2表示第n个机器人运行到任务要求货架处花费的时间。
根据评价函数,将所有的机器人分成2类,1) 正在执行当前任务;2) 处于空闲状态。分别计算等待代价和路径代价,再根据两者之和对所有的机器人进行评价,选取总代价gn最小的机器人承担任务。
针对前述物流任务的第3个步骤进行优化,应使机器人搬运的货架尽快停放在空闲区域内,从而使得机器人可以继续执行下一个任务。因此,选取距离起点(机器人的当前位置)最近的一个空闲位置停放。使用曼哈顿距离估计代价:
| ${g_n} = {\rm{abs}}\left( {{\rm{cur}}.x - n.x} \right) + {\rm{abs}}\left( {{\rm{cur}}.y - n.y} \right)$ | (2) |
式中:gn表示停放到第n个存放位置的代价。cur.x 表示当前点的横坐标,cur.y 表示当前点的纵坐标。n.x表示第n个存放位置的横坐标,n.y表示第n个存放位置的纵坐标。abs表示求绝对值的函数。
2.2 特殊规则约束下基于A*算法的路径规划在设计的仓储空间结构中,目前,应用于多机器人系统运动规划的方法有人工势场法[3-4]、神经网络[5-6]、模糊逻辑[7-8]、A*等算法。其中,A*算法已经得到了广泛地应用,而且能够保证找到最优的求解路径[9-10]。考虑仓储空间结构中道路单向运行的约束,在A*算法的基础上进行修正和改进。
A*算法的基本流程是从起始点开始,根据估计代价选择性地扩展节点,直到将目标点扩展进来。关键是选择合适的评价函数:
| $f\left( n \right) = g\left( n \right) + h\left( n \right)$ | (3) |
式中:f(n)代表从起始点经过节点n到达目标点的预估代价。g(n)代表从起始点到节点n的真实代价。f(n)代表从节点n到目标点的估计代价。
考虑到仓库环境中所有的道路均为单行线,在单行线上扩展节点是单向且有序的,如图 4所示,沿纵向道路L1从n1扩展的后继节点依次是n2、n3、n4、n5、n6、n7。 而其中n2、n3以及n5、n6是顺次扩展的固定流程,关键只在于在n4、n6节点处是否转向到横向道路H2、H3。为简化步骤,将A*算法中以网格为节点扩展路径修改成以道路为节点扩展路径。由此,一条完整路径可以表示为起始点-道路1-道路2…道路n-目标点。如图 4所示,沿纵向道路L1从n1扩展的后继节点依次是n2、n3,代表横向道路H2、H3。
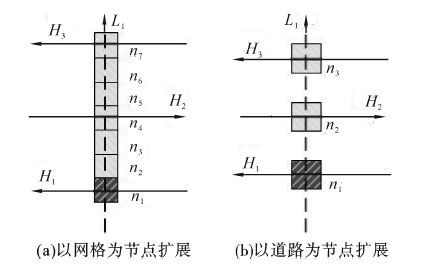
|
| 图 4 A*算法路径规划的节点拓展 Fig. 4 Node expansion of A* path planning |
以道路为节点减少了扩展次数,节省了时间。但是,路径的起点和终点不一定是道路,还有可能是货架所在的存放空间。所以,需要加入特殊情况处理,将节点扩展分为3种情况:道路扩展道路、起点扩展道路、道路扩展终点。
当前节点是货架(起点),则可扩展的节点为相邻道路上的相邻位置。如图 5(a)所示,黑色方块为货架n1,浅色方块为可扩展的后续节点,节点n2即纵向道路L1,节点n3即横向道路H1。当前节点是道路,则可扩展的节点为与此道路交叉的且在道路前方的所有道路。如图 5(b)所示,黑色方块为节点n1,即纵向道路L1。浅色方块为可以扩展的节点,包括节点n2,横向道路H2;节点n3,横向道路H3;节点n4,横向道路H4。
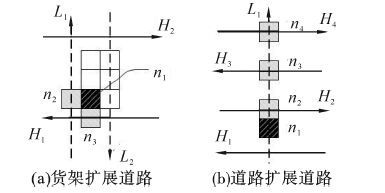
|
| 图 5 从货架和道路扩展到道路 Fig. 5 Expansion from shelf or road to road |
当前节点所在的道路与目标点相邻,则扩展当前点时可以加入目标点。如图 6所示,当前点n1扩展后继节点n2,即纵向道路L1。纵向道路L1与黑色方块目标点相邻。因此,n2可以扩展目标点n3。
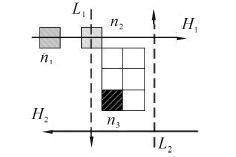
|
| 图 6 扩展目标点 Fig. 6 Expand destination |
以道路为基本节点,评价函数需要相应的调整。除了基本的曼哈顿距离,还需要根据道路的方向加上相应的转向代价,如图 7所示。
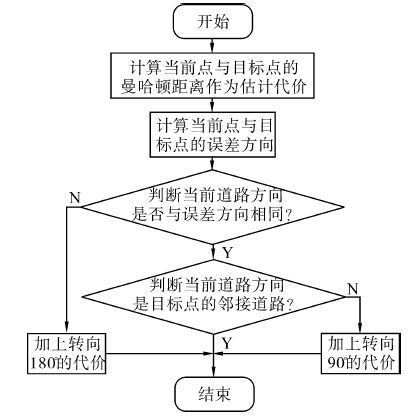
|
| 图 7 估价函数h(n) Fig. 7 Cost function h(n) |
如果预先知道每个时刻各机器人的具体位置,就可以在路径规划时预测并避免可能发生的道路冲突。为此,可以设置“时空运行地图”,记录下每个机器人随时间运行的轨迹,把规划出的机器人轨迹记录下来形成一张“横-纵-时间”的三维地图,作为轨迹规划的参考。仍然基于A*算法进行规划,但是将F、G、H的路径代价替换为时间代价。同时,在考虑运动到某个位置的路程的基础上,进一步加入因防止碰撞而增加的等待时间代价。由此,在路径规划中考虑了冲突延时,可以减少规划出的路径产生冲突。
由于道路的单向性,规划的先后顺序并不能够保证运行时的优先级。如果后规划的任务插入到先规划的任务道路前方,那么也只能由在道路后方的先规划的任务等待。这样就导致实际的轨迹跟原有的规划不完全符合。在这种情况下,任务仍然能够根据规划出来的路径完成,只是时间可能不合拍。如果继续根据有时间偏差的时空运行地图去规划新的任务,误差会积累,虽然任务仍然能够完成,但是路径不是最优。为此,修正路径规划方法,在每一次非规划的避让发生之后及时修正时空运行地图,使得地图与实际相符。
2.4 碰撞预防已经为了避免可能发生的碰撞,设置独占点。在某个时刻某个位置只能由一个移动机器人独自占用。同一时刻的其他机器人想要进入此位置必须等待。在实际系统中,这可以由安装在机器人上的超声波或红外传感器实现。在检测到与其他机器人距离小于警戒值的情况下,紧急刹车,防止碰撞。
3 仿真实验通过仿真实验,检验智能调度和路径规划方法是否有效,并进一步研究机器人的数量配置对任务执行效率的影响。仿真程序和结果都在 MATLAB 2013a (Math Works Corporation,USA) 上完成。
3.1 任务生成和实验设定为保证仿真实验结果的客观性,要避免受到任务本身特点可能带来的的影响。为此:
1) 采用随机算法产生任务。货架与机器人的初始位置也随机产生。任务调用的货架编号和入货口/出货口符合随机高斯分布。
2) 任务数量设为1 000,随机产生10组任务。移动机器人的数量分别设定为10、20、30、40和50共5种情况。每种情况下,利用智能调度算法和2种路径规划算法完成给定的10组任务。总共进行了100次实验。
3.2 实验结果在进行的100次实验中,所有任务都顺利完成,验证了仓储空间架构设计、智能调度和路径规划方法的可行性和有效性。
表 1中,利用双因子方差分析评价机器人数量和路径规划算法对于完成物流任务所运行总里程、耗费时间以及抢路冲突的影响(置信度p=0.05)。机器人的数量配置对于运行总里程、耗费时间和抢路冲突具有显著的影响,而2种路径规划算法在运行总里程和耗费时间这两方面没有体现出显著差别,但是在抢路冲突方面表现出了明显的差别。
| p | 运行总里程 | 耗费时间 | 抢路冲突 |
| 机器人数量 | <10-4 | <10-4 | <10-4 |
| 路径规划算法 | 0.969 0 | 0.919 9 | 0.000 3 |
图 8给出了不同数量配置的机器人集群在2种路径规划算法下完成1 000个任务所运行总里程的10次实验平均值。随着机器人数量的增加,机器人集群完成设定任务所运行的总里程逐渐降低。增加的机器人为系统的调度提供了更大的灵活度,可以选择与任务货架距离更近的机器人承担物流任务。
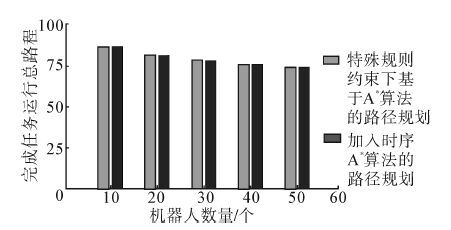
|
| 图 8 完成设定任务运行总里程随机器人数量的增加而减少 Fig. 8 The total pathway decreases as robot number increases |
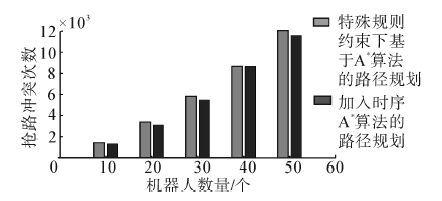
图 9给出了不同数量配置的机器人在2种路径规划算法下完成1 000个任务耗费时间的10次实验平均值。随着机器人数量的增加,完成设定任务所耗费的总时间明显降低。但是同时,所需要协调的抢路冲突也明显增加,如图 10所示。
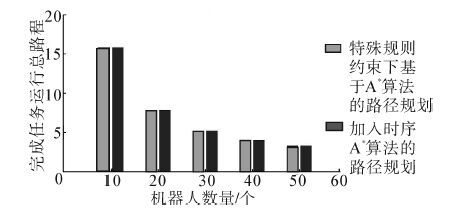
|
| 图 9 完成设定任务耗费时间随机器人数量的增加而降低 Fig. 9 Running time decreases as robot number increases |
|
| 图 10 运行中发生的抢路冲突随机器人数量的增加而增加 Fig. 10 Conflicts increases as robot number increases |
由图 8和图 9可以直观看出,在特殊道路规则的约束下,基于修正的A*算法和加入时序的A*算法这2种路径规划方法在完成任务运行总路程和耗费时间2个方面,表现接近。加入了时序的路径规划算法,降低了运行中发生的抢路次数,如图 10所示。但是,在仓储空间中道路单向运行设定的约束下,加入时序的A*算法无法全部避免抢路冲突,冲突次数随着机器人数量的增加而明显上升。
4 结束语电子商务的迅猛发展为仓储物流带来了新的需求和挑战,本文对应用移动机器人技术发展新一代的智能仓储物流进行了探索。建立了一个灵活可重构的仓储空间模型,制订了执行物流任务的移动机器人集群的运行规则,对智能调度和路径规划进行了方法研究和仿真验证。由此表明,基于移动机器人集群的自动化仓储技术有望在电子商务物流中起到颠覆性的关键作用。
本文中,订单是按照时间顺序发送给机器人中心控制系统的。将来,可以对订单分批优化之后再释放,能够更加有效地对机器人进行调度和规划。
| [1] | 邹爽心. 仓储机器人的应用现状与发展战略探讨[J]. 物流工程与管理,2013, 35 (6) : 171 –172. ZOU Shuangxin. The present and future of warehouse robot[J]. Logistics Engineering and Management,2013, 35 (6) : 171 –172. |
| [2] | 曹宝文. 自动化仓库中多AGV系统路径规划研究[D]. 天津: 南开大学, 2012: 21-23. CAO Baowen. Path planning of multi-AGV system in automatic warehouse[D]. Tianjin: Nankai University, 2012: 21-23. |
| [3] | 张建英, 赵志萍, 刘暾. 基于人工势场法的机器人路径规划[J]. 哈尔滨工业大学学报,2006, 38 (8) : 1306 –1309. ZHANG Jianying, ZHAO Zhiping, LIU Tun. A path planning method for mobile robot based on artificial potential field[J]. Journal of Harbin Institute of Technology,2006, 38 (8) : 1306 –1309. |
| [4] | 于振中, 闫继宏, 赵杰, 等. 改进人工势场法的移动机器人路径规划[J]. 哈尔滨工业大学学报,2011, 43 (1) : 50 –55. YU Zhenzhong, YAN Jihong, ZHAO Jie, et al. Mobile robot path planning based on improved artificial potential field method[J]. Journal of Harbin Institute of Technology,2011, 43 (1) : 50 –55. |
| [5] | 黄磊. 基于神经网络的移动机器人路径规划研究[D]. 武汉: 武汉理工大学, 2008: 17-27. HUANG Lei. Research on path planning of mobile robots based on neural networks[D]. Wuhan: Wuhan University of Technology, 2008: 17-27. |
| [6] | 陈华志, 谢存禧, 曾德怀. 基于神经网络的移动机器人路径规划算法的仿真[J]. 华南理工大学学报:自然科学版,2003, 31 (6) : 56 –59. CHEN Huazhi, XIE Cunxi, ZENG Dehuai. Simulation of path planning algorithm of mobile robots based on neural networks[J]. Journal of South China University of Technology: Natural Science,2003, 31 (6) : 56 –59. |
| [7] | 苏治宝, 陆际联. 用模糊逻辑法对移动机器人进行路径规划的研究[J]. 北京理工大学学报,2003, 23 (3) : 290 –293. SU Zhibao, LU Jilian. A study on the path planning of mobile robot with the fuzzy logic method[J]. Transactions of Beijing Institute of Technology,2003, 23 (3) : 290 –293. |
| [8] | 卓睿, 陈宗海, 陈春林. 基于强化学习和模糊逻辑的移动机器人导航[J]. 计算机仿真,2005, 22 (8) : 157 –162. ZHUO Rui, CHEN Zonghai, CHEN Chunlin. Navigation for mobile robots using reinforcement learning and fuzzy logic[J]. Computer Simulation,2005, 22 (8) : 157 –162. |
| [9] | HART P E, NILSSON N J, RAPHAEL B. A formal basis for the heuristic determination of minimum cost paths[J]. IEEE Transactions on Systems Science and Cybernetics,1968, 4 (2) : 100 –107. |
| [10] | 王勇. 智能仓库系统多移动机器人路劲规划研究[D]. 哈尔滨: 哈尔滨工业大学, 2010: 19-30. WANG Yong. Research about path planning of multiple mobile robots in intelligent warehouse system[D]. Harbin: Harbin Institute of Technology, 2010: 19-30. |



