4 正反命题与谓词演算系统 4.1 正反命题演算系统Lα
在经典系统L上引入“正反集对偶变换公理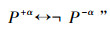
1)初始符号(略);
2)命题的形成规则(略);
3)定义(略);
4)公理。
(1)正集公理
 |
(2)正反集对偶变换公理
L0:
(3)反集公理
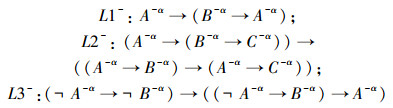 |
5)演绎推理规则
分离规则:若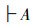
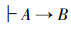

定义1 系统Lα
由以上1)~5)几个部分组成的公理系统,可以叫做系统Lα。
定理1 经典逻辑的定理封闭域上的有效性
在系统Lα中,相同集+α,-α中的命题演算,所有经典逻辑的定理与演算模式都是有效的。
证明 略。
定理2 正、反集上的等价替换
系统Lα中,设F(M,N)表示含有变项M、N的命题公式,则如果在相同集中的经典命题
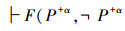


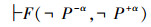
证明 略。
系统Lα的语义很简单,用二值真值表定义为
定义2 单一正集上的真值表
| A+α | ¬A+α |
| 1 | 0 |
| 0 | 1 |
| A+α | B+α | A+α→B+α |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
| 0 | 0 | 1 |
| 0 | 1 | 1 |
| A-α | ¬A-α |
| 1 | 0 |
| 0 | 1 |
| A-α | B-α | A-α→B-α |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
| 0 | 0 | 1 |
| 0 | 1 | 1 |
定义4 跨正反集上的真值表(如表 5)。
| P+α | P-α |
| 1 | 0 |
| 0 | 1 |
在表中可以看出经典二值真值表定义仍然不变,增加了一个跨正反集上的真值表定义。
在系统Lα中,利用以上“真值表”可以证明,下列公式是不可证的。
公式P+α,

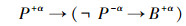

1)基本符号(略)
2)定义(略)
3)公理
(1)正集公理
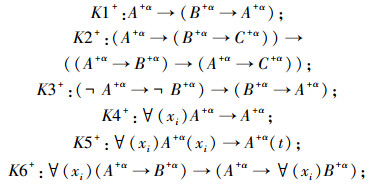 |
(2)正反集对偶变换公理
K0:
(3)反集公理
 |
4)系统内推理规则
R1 分离规则:若

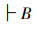
R2 概括规则:若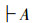

定义5 系统Kα
由以上1)~4)几个部分组成的公理系统,叫做系统Kα。
在系统Kα中,具有与Lα类似的定理(证明与Lα相同),即:
定理3 经典逻辑的定理封闭域上的有效性
在系统Kα中,相同集+α,-α中的命题演算,所有经典逻辑的定理与演算模式都是有效的。
定理4 正、反集上的等价替换
系统Kα中,设F(M,N)表示含有变项M、N的命题公式,则如果在相同集中的经典命题F(Pα,¬Pα)成立(即F(P+α,¬P+α)且F(P-α,¬P-α)成立),则在不同集中F(P+α,P-α),且├F(¬P-α,¬P+α)也成立。
在不同集中,含有量词的公式,可以用下列公式转换:
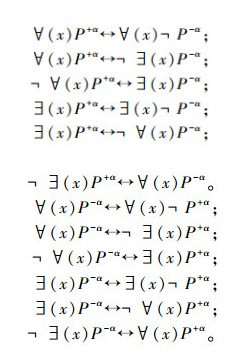 |
Kα的语义解释(略)[3]
4.3 系统Lα、Kα的完全性与不可判定命题根据“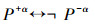

注记1 Pe是U外不动项命题,是未定义命题,不参与演算。
定理5 Lα等价系统
系统Lα在+α与-α中的全部公式可以翻译成经典命题演算系统L的公式,即系统Lα在+α与-α中与经典命题演算系统L等价。
证明 略
定理6 Kα等价系统
系统Kα中全部公式可翻译成经典谓词演算系统的公式,即系统Kα与经典谓词演算系统K等价。
证明 略
由于系统Kα与经典谓词演算系统K等价,所以经典逻辑的元定理在系统Kα仍然成立,根据“定理5、6”很容易证明以下定理。证明方法同经典谓词逻辑系统方法,这里不再给出。
系统L的一致性、可判定性、完全性等元定理,在系统Lα中都是有效的;
系统K的一致性、不可判定性、完全性等元定理,在系统Kα中都是有效的;
定理7 Pe是域外命题
命题Pe在系统Lα中是未定义命题,是域外命题;
证明设P是U的一个完全划分,
在命题演算Lα中,若+α=-α=e(P是+α,-α的一个完全划分),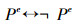
因此,在命题演算Lα中,若+α=-α=e,则Pe是不动命题,e,Pe在U上无定义;
未定义命题与其他命题的混合演算,如
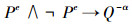
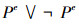
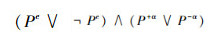
定理8 系统Lα完全性定理
在系统Lα中,若

证明 因为Lα⇔L,而系统L是完全的,即:
若
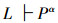
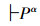
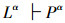
所以,系统Lα也是完全的。
定理9 Pe是不可判定命题
命题Pe在系统Lα中是不可判定命题(证明略,因为不动命题是不可判定命题)。
注记2 悖论Pe不参与系统演算
1)虽然系统Lα中出现了悖论Pe,但是,Pe是未定义命题,不参与系统演算,不会导致系统Lα演算崩溃,系统Lα仍然是有效的。
2)虽然系统Lα中出现了不可判定Pe,但是,Pe与系统完全性无关,系统Lα仍然是完全的,系统Lα的定理集合是可判定的。
定理10 P(xP)是域外命题
命题P(xP)在系统Kα中是未定义命题;
证明同上,在谓词演算中,若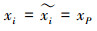
与系统Lα一样,未定义命题P(xP)与其他命题的混合演算,如

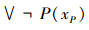
定理11 系统Kα完全性定理
系统Kα中,若

证明 因为Kα⇔K,而系统K是完全的,即
若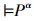
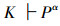
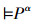

所以,系统Kα也是完全的。
定理12 P(xP)是不可判定命题
命题P(xP)在系统Kα中是不可判定命题(证明略,因为不动命题是不可判定命题)。
注记3 悖论P(xP)不参与系统演算
1)虽然系统Kα中出现了悖论P(xP),但是,P(xP)是未定义命题,不参与系统演算,不会导致系统Kα演算崩溃,系统Kα仍然是有效的。
2)虽然系统Kα中出现了不可判定P(xP),但是,P(xP)与系统完全性无关,系统Kα仍是完全的。
4.4 经典逻辑定理的适用范围定义6 超协调逻辑系统
正反命题演算系统“Lα”与正反谓词系统“Kα”也称超协调逻辑系统。
在超协调系统中,可以发现经典逻辑是定义在一个已知集合U上的,不能无限制地使用到U外,经典逻辑的推理有一个使用范围。
定理13 经典逻辑的适用范围
U=x1,x2,x3,…,xn,…是一个已经定义集合,经典逻辑的所有定理只适用于已经定义的集合U上。
证明 设U=+α∪-α是一个已定义集合;
假设在这个已定义集合外,可以适用经典逻辑的所有定理,根据U外不动项定理,
那么,有矛盾命题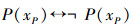
根据邓—斯各特定理(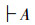


所以,经典逻辑的所有定理只适用于已经定义的集合U上。
定理14 “反证法”的适用范围
U=x1,x2,x3,…,xn,…是一个已经定义集合,“反证法”只适用于已经定义的集合U上。
证明 因为,反证法是经典逻辑的一条定理,即:如果
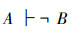

根据定理13,“反证法”只适用于已经定义的集合U上。
定理15 不动项矛盾用于“反证法”的限制
U=x1,x2,x3,…,xn,…是一个已经定义集合,不动项矛盾不能作为“反证法”在已定义的集合U上的推理依据。
证明 因为根据U外不动项定理,不动项矛盾是已定义集合外的矛盾;
假设不动项矛盾能作为“反证法”在已定义的集合上的推理依据。
那么,有矛盾命题
根据邓—斯各特定理(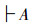

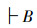
如果不动项矛盾能作为“反证法”在已定义的集合U上的推理依据,将建立不起来任何足道的系统;
所以,不动项矛盾不能作为“反证法”在已定义的集合U上的推理依据。
在 逻 辑 系 统 Lα、Kα中,若U=x1,x2,x3,…,xn,…是已定义集合,P是U上的任意一个有定义的性质,若xi∈U,则P(xi)、

推论1 构造悖论,不能作为“反证法”在已定义的集合U上的推理依据。
例1 构造悖论的错误证明方法
举出一个具体的例子,U为全体整数集合U=J,假设在n=n中,任意n∈J;把U=J分成偶数集合与奇数集合:
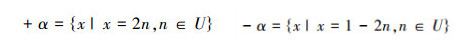 |
P(x)代表谓词“x是偶数”,¬P(x)代表谓词“x是奇数”;n∈+α,或者n∈-α;定义一个新数T=1-n;自指代T=n,n=1-n,n是偶数↔n是奇数;产生悖论,不可判定命题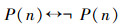
 |
根据反证法得到,
例2 相对无意义的命题
设U为全体整数集合,P(x):表示x是偶数;则P(0),P(2),P(7),…等都是有定义、有意义的命题;
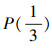
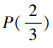
U=x1,x2,x3,…,xn,…是一个已经定义集合,如果

注记5 “反证法”的正确推理形式
一般地,设U=+α∪-α是一个已定义集合,xi∈U,K(xi)是U内的任意一个命题,根据U外不动项定理,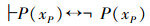
1)U外不动项所产生的矛盾,使用“反证法”只能得出xP∉U。即把xP∈U看成假设时,可以使用“反证法”进行推理,正确的推理形式是:
 |
2)U外不动项所产生的矛盾,不能作为任何“U内演算的推理依据”即把xP∈U看成真命题时,使用“反证法”是错误的。不正确的推理形式是:
 |
3)一般使用“自指代”所产生的矛盾,都是域外矛盾,不能作为反证法的依据。
可以回顾一下,历史上“直觉主义”者,也认识到无限制地使用“反证法”会有问题,他们转向完全的“构造数学”,他们也看到一些问题,但是,没有把问题完全搞清。这里真正看到“反证法”的使用范围。
5 无穷集合的幂集中的不可判定命题集合论的创立者Cantor证明:无穷集合的幂集合不能与原来的集合建立一一对应关系。可以回顾一下其证明过程,使用Cantor的对角线方法。
如果PM为M的幂集,且M~PM(M与PM之间可以建立一一对应关系,即双射关系),则存在T,T⊆M,且T∉PM。
对于一个M子集而言,如果能够决定M的元素中哪些属于该子集,那么M的子集就确定了。可以给出一个一般准则,由它可以对M的任何元素x,决定该元素是否属于该子集。
在假设M~PM中,任意x∈M对应一个y∈PM,即:x∈M↔y∈PM,
y是M的子集之一,y⊆M,
x∈y,或者x∉y;规定:x∈y↔x∉T;x∉y↔x∈T;
假定T∈PM,M~PM,存在
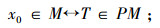 |
按规定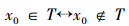
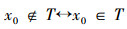
矛盾,所以,T∉PM。
注:这证明在很多“数理逻辑”书中都可以见到,如《元数学导论》[7]。
5.1 无穷集合演算中的不动项在以上证明过程中,构造的集合T,如果按照正反集合分析法,实际上是一个不动项,证明如下。
定理16 无穷集合演算中存在不动项
如果无穷集合与它的幂集合之间能建立一一映射,那么,幂集合演算中存在一个不动项。
证明 首先把以上证明过程,整理如下:
假设在双射关系F:M~PM中,任意x∈M对应一个F(x)∈PM,
即:

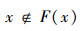
规定:

假定

按规定: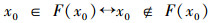
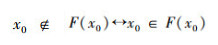
 |
按规定:

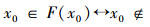

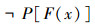

命题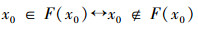

如 果 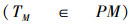
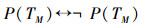
这是“Cantor的对角线方法”证明,在这个证明中,他把TM看成是一个已知项TM∈U,实际上TM∈U未必成立,他只证明了以下结果:
如果双射关系F:M~PM成立,且TM∈U,那么,
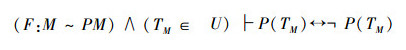
上面命题中出现了两个假设,到底是哪个假设引起的矛盾,还要分析。
这个定理和下面的定理等价,下面证明“Cantor的对角线方法”表现更清晰。
定理17 自然数集合演算中存在不动项
如果自然数集合与它的幂集合之间能建立一一映射,那么,它的幂集合演算中存在一个不动项。
证明 这个定理可以看成定理16的特例,证明过程与定理16相同。
双射关系F:ω~P(ω),ω是自然数集合,P(ω)是ω的幂集合。
假设在F:ω~P(ω)中,任意n∈ω对应一个
即: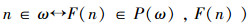
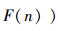

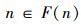
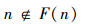
按规定: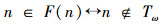
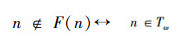
假定


按规定:
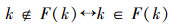
再把P(ω)分为正反集合,设:
 |
按规定: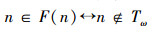
自我指代:Tω=F(k);
即

P[F(n)]表示n∈F(n);则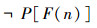

命题


如果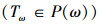

即如果双射关系
同样以上证明有两个假设,可以表示为
如果双射关系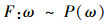
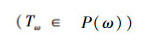

即: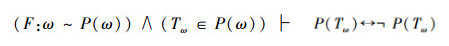
注记6 “Cantor的对角线方法”
假设自然数和它的幂集合有一一对应关系,即
F(1)=1,∗,3,4,∗,…,该集合包含1,3,4,不包含2,5,(空缺的用“∗”标注);
F(2)=1,∗,3,∗,∗,…,该集合包含1,3,不包含2,4,5;
F(3)=1,∗,3,∗,5,…,该集合包含,1,3,5,不包含2,4;
F(4)=1,2,3,∗,5,…,该集合包含1,2,3,5,不包含,4;
F(5)=∗,2,3,∗,5,…,该集合包含2,3,5,不包含1,4;
…

定义一个新集合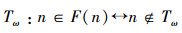

显然集合Tω=∗,2,∗,4,∗,…是上面集合序列对角线元素的集合在ω上的补集;
Tω也是ω的子集,Tω∈P(ω),它也在上表中,设它对应F(k),Tω=F(k);
得到矛盾:
注记7 Cantor的两个定理
1)自然数集合的任意一个子集都可以与一个0与1的序列建立一一映射关系。
证明 用一个函数来表示某自然数的集值域,在属于该集的自然数处它取值0,在不属于该集的自然数处它取值1。某自然数集合代表的函数值的序列便是由0与1组成的无穷序列。为表示方便把自 然 数 集 合 中 的 0 排 除,仅为ω=1,2,3,4,5,6,…,P(ω)为ω的幂集合。
例:A1=1,∗,3,4,∗,…该集合包含1,3,4,不包含2,5,(空缺的用“∗”标注)该序列为F(A1)=01001…;
A2=1,∗,3,∗,∗,…该集合包含1,3,不包含2,4,5,该序列为F(A2)=01011…;
A3=1,∗,3,∗,5,…该集合包含,1,3,5,不包含2,4,该序列为F(A3)=01010…;
A4=1,2,3,∗,5,…该集合包含1,2,3,5,不包含,4,该序列为F(A4)=00010…;
A5=∗,2,3,∗,5,…该集合包含2,3,5,不包含1,4,该序列为F(A5)=10010…;
…
所以,自然数集合的任意一个子集都可以表示成一个0与1的序列,即自然数集合的任意一个子集都可以与一个0与1的序列建立一一映射关系。
2)全体实数与全体自然数集合的子集具有一一映射关系。
以上两个定理已经被Cantor等证明,自然数集合的任意一个子集都可以表示成一个0与1的序列,任意实数都可以表示二进制0与1的序列,它们之间具有一一映射关系[7]。
定理18 实数集合演算中存在不动项
如果自然数集合与实数集合之间能建立一一映射,那么,实数集合演算中存在一个不动项。
证明 由于全体实数都可以化成二进制形式,只用0,1两个数字表示,注记7构造的F(Ai)序列实际上可以看成与实数之间有一个一一对应关系,用xi表示这些实数,用Cantor对角线法构造的不动项,也可以看成实数领域的不动项。
把这些序列列成无穷方阵:
F(A1)=x1=01001…
F(A2)=x2=01011…
F(A3)=x3=01010…
F(A4)=x4=x00010…
F(A5)=x5=x10010…
…
用对角线法在上面方阵中构造一个对角线数:01010…,把这个对角线数0与1互相交换得TR,TR=10101…,TR和上表中任何一个都不同。
用Tn表示TR的第n个数字,xnn表示xn的第n行,第n个数字,则TR的定义可以表示为
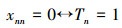
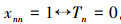
如果TR也是实数,TR∈R,设它排列在第k行,现在考查TR是序列xk中第k位Tk,按定义得到以下矛盾:

设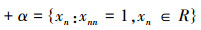

按规定
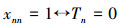
自我指代:xk=TR,xkk=Tk,(Tk是TR的第k项);
即: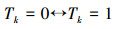

P(xk):xkk=1(xk的第k项为1);
如果TR∈R,则有“TR的第k项为1”⇔“TR的第k项为0”;
即有
即如果TR∈R,则有悖论:
所以,如果自然数集合与实数集合之间能建立一一映射,那么,实数集合演算中存在一个不动项。
同样以上证明有两个假设,可以表示为:
如果双射关系F:ω~R成立,且TR∈R,那么,
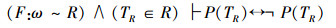 |
运用这种对角线方法,在有理数集合上,同样可以构造出不动项矛盾。
因为不动项命题都是不可判定命题,所以,以下推论成立。
推论2 如果双射关系F:M~PM成立,且TM∈PM,那么,P(TM)是不可判定命题。
推论3 如果双射关系F:ω~P(ω)成立,且Tω∈P(ω),那么,P(Tω)是不可判定命题。
推论4 如果双射关系F:ω~R成立,且TR∈R,那么,P(TR)是不可判定命题。
5.2 “对角线方法”的逻辑分析Cantor对角线方法是经典集合论、证明论、模型论、递归论中的一个重要方法,如:实数不可数、图灵机不可判定、存在非递归函数等很多定理的证明都是使用这种方法。然而,以下的证明表明,对角线方法产生的是U外不动项,这说明使用对角线方法证明的定理的证明是错误的。
定理19 广义U外不动项定理
设全集U=x1,x2,…,xi,…是一个已经定义的集合,P是定义在U上的一个性质,命题P是关于+α、-α的一个划分,即:
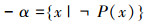
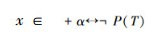
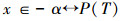
证明 
假设
同理,
假设
因为,
所以,假设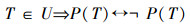
所以,
“广义U外不动项定理”可以简化为:
P、T在U上可定义,
T∈U,
在以上定理中,如果+α,-α之间存在双射关系,即f:+α~-α,
则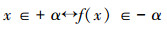
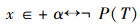

所以,
即为“U外不动项定理”,可以看出“广义U外不动项定理”是“U外不动项定理”的推广形式,“U外不动项定理”是它的特例。
例3 “广义U外不动项定理”的具体例子
以上定理16~18中,“Cantor对角线证明方法”可以看成把U分成对称的+α,-α,定义新项“T”满足

定理16规定:
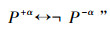
定理17规定:

定理18规定: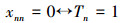

以上构造项TM、Tω、TR都满足:
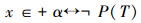

所以,TM、Tω、TR都是U外不动项。
“对角线方法”还可以看成一种非对称的分类方法,也是“广义U外不动项定理”的特例。
定理20 “对角线证明方法”的非对称分类
如果集U上的演算是一致的,+α=U,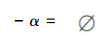
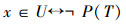
证明 在以上“广义U外不动项定理”中假设+α=U,则

1)假设
2) 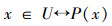
3) 
4) 
5)假设T∈U——问T∈U吗?假设T∈U成立,那么存在某个x,x=T。
6) 
根据“广义U外不动项定理”的形式:P、T在U上可定义,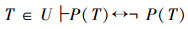
“P、T在U上可定义”,即“U上元素上可列表”,即双射关系F:ω~U成立。
“对角线证明方法”可以简化为
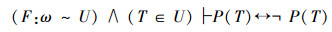
注记8 “对角线证明方法”的二元谓词表示法
设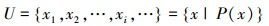
表中的第i个元素xi的第n项记为P(xi,n),可以把按对角线方法排列如下:
 |
定义一个新的项T,满足T的第n项,不同于xn的第n项,
即: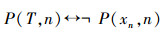
问T∈U吗?假设T∈U成立,那么存在某个xk,xk=T,
即:

对角线方法使用全集(补集合为空集非对称分类方法),所有“对角线方法”都是一个类型,它们都是“广义U外不动项定理”的特例。所以,“Cantor对角线方法”构造的实数也是“广义U外不动项定理”的特例。
推论5如果实数集R上的演算是一致的,那么,“康托的对角线方法”所构造的项T满足: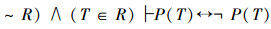
定理21 “对角线证明方法”的3个结论
设U=x1,x2,…,xi,…,如果U内演算是一致的,“对角线证明方法”可以得到以下3个结论:
(A)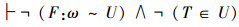
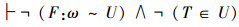
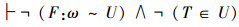
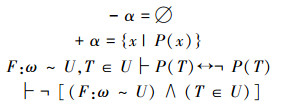 |
(1) |
由于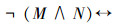
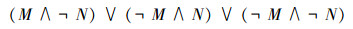 |
由式(1)可以得到以下3个结论:
(A)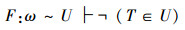
 |
(B)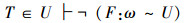
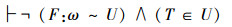 |
(C) 
注记9 Cantor的断定
在“对角线证明方法”A、B、C 3个结论中,如果T∈U成立,那么,双射关系F:ω~U一定不成立,这就是Cantor的断定,即B结论正确;
另外一种情况是:如果T∉U,那么,双射关系F:ω~U可能成立,也可能不成立,即:A、C都可能正确,这说明矛盾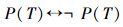
下面的证明表明:矛盾恰恰是由T∈U引起的,Cantor的断定是错误的。
定理22 不动项矛盾与双射关系无关
设U=x1,x2,…,xi,…,如果U内演算是一致的,则Cantor“对角线证明方法”F:ω~U,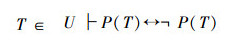
即:
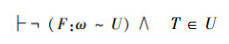
证明 只要否定“结论(B) 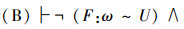
1)假设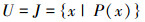
2) 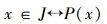
3) 
把U=J分成偶数集合与奇数集合:
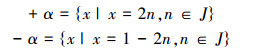 |
x∈J,即:x∈+α,或者x∈-α定义一个新数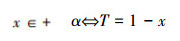
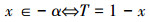
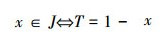
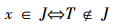

4) 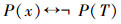
5)假设T∈J——问T∈J吗?假设T∈J成立,那么存在某个x,x=T。
6) 
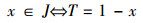

7) 

由于T=1-T,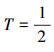
所以: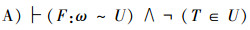
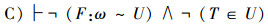
即:不动项矛盾的存在与双射关系:F:ω~U无关。
根据不动项的性质,以下推论都成立:
推论6 如果集U上的演算是一致的,“对角线方法构造项T”一定在U外,T∉U。
推论7 如果集U上的演算是一致的,“对角线方法构造项T”是未定义项。
推论8 如果集U上的演算是一致的,“对角线方法构造项T”,P(T)是不可判定命题。
推论9 如果集U上的演算是一致的,“对角线方法构造项T”,P(T)的不可判定与U内项是否可以判定无关。
推论10 如果集U上的演算是一致的,“对角线方法构造项T”,
推论11 如果集U上的演算是一致的,“对角线方法构造项T”不能作为任何“U内演算的推理依据”。
推论12 如果集U上的演算是一致的,那么,满足对角线方法的构造项T,断定T∈U的所有“对角线方法”证明错误。
注记10 广义域外不动项定理解释
1)在以上定理证明过程中,根据“反证法的使用规则”,把xP∈U看成假设时,可以使用“反证法”进行推理,只能得出xP∉U;把xP∈U看成真命题时,使用“反证法”是错误的。
2)“U外不动项定理”与“广义U外不动项定理”都是用二分法把全集U分成两类性质集合,命题P是关于U的一个划分,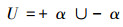
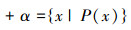

3)“U外不动项定理”与“广义U外不动项定理”的本质是:一个U中已经定义的项与其否定项不能自指代。如果自指代,就会变异成一个新项“T”,这个新项“T”不再是U的元素,即:T∉U。
4)“U外不动项定理”与“广义U外不动项定理”的区别是:“U外不动项定理”要求+α,-α之间存在双射关系,即:f:+α~-α;“广义U外不动项定理”没有这个要求。
5)“Cantor对角线方法”可以看成是U上的一个特殊的分类。从“U外不动项定理”的分类看,使用自然数标号与它对应的第n项分类,这个分类恰与双射关系U~ω联系在一起;从“广义U外不动项定理”的分类看,+α=R,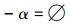
还可以举出一个具体的例子:
例4 有理数集合上的对角线方法
假设在没有发现无理数之前,不知道有无理数,只知道所有的数都为有理数。按照Cantor对角线方法,同样可以证明:有理数集合是不可数的。
假设把有理数区间[0,1]里的所有数按照某种顺序排列起来,那么总能找到至少一个0到1之间的有理数不在列表里。把列表上的数全写成0到1之间的小数:
a1=0.0143634628…
a2=0.3794907237…
a3=0.2334343423…
a4=0.0005948211…
a5=0.9590129145…
…
那么就构造这么一个小数T,小数点后第1位不等于a1的第1位,小数点后第2位不等于a2的第2位,总之小数点后第i位不等于ai的第i位。这个数属于有理数区间[0,1],但它显然不在你的列表里。这样,就证明了有理数集合是不可数的。
也许你会说,你构造的这个数T已经不是有理数,是一个和有理数具有不同性质的新的数。当然,现在知道有理数外还有无理数,即(T∉Q)。
即ω是自然数集合,Q全体正有理数集合,假设双射关系F:ω~Q成立。
按照对角线方法,同样可以找到一个数T,导致矛盾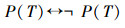
即
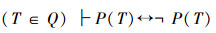

在证明实数不可数时,ω是自然数集合,R为全体实数集合,假设双射关系F:ω~R成立,按照对角线方法,同样可以找到一个数TR,导致矛盾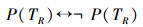

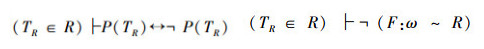

对比这2个推理过程
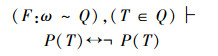 |
(1) |
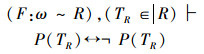 |
(2) |
在前一个矛盾(1)中否定了T∈Q,没有否定F:ω~Q;而后一个矛盾(2)中却否定了F:ω~R,而没有否定TR∈R。
对角线证明方法具有统一的形式,矛盾只能有一个统一的产生根源,实际上,前一个否定是正确的,后一个否定是错误的。
即矛盾是由TR∈R引起的,并不是双射关系F:ω~R产生的,这说明“如果实数域演算是一致的,那么TR∉R。
例5 有理数集合上的域外不动项
U为全体正有理数集合U=Q,假设双射关系F:ω~Q成立,ω是自然数集合,Q为全体正有理数集合。
假设在F:ω~Q中,任意n∈ω对应一个F(n)∈Q,即:
把U=Q分成正反集合,
正集:平方大于2的有理数集合,即:
反集:平方小于2的有理数集合,即: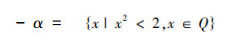
F(n)∈+α,或者F(n)∈-α;
定义一个新数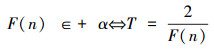
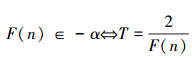
因为F:ω~Q成立,
所以,存在
按规定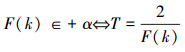
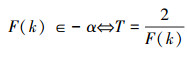
自指代,让T=F(k),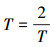
产生悖论,不可判定命题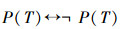
由于这个矛盾的产生,就责怪双射关系F:ω~Q不能成立,这显然是错误的。其实,
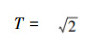

例6 实数集合上的域外不动项
仿照Cantor的对角线方法,
U为不为0的全体实数集合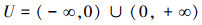
假设双射关系F:ω~U成立,ω是自然数集合。
假设在F:ω~U中,任意n∈ω对应一个F(n)∈U,即: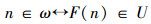
把U分成正数集合与负数集合:
 |
F(n)∈+α,或者F(n)∈-α
定义一个新数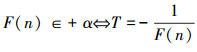
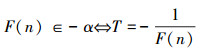
因为F:ω~U成立,所以,存在:
 |
按规定
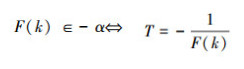
自指代T=F(k),
产生悖论,不可判定命题
由于这个矛盾的产生,就责怪双射关系F:ω~U不能成立,这显然是错误的。其实,

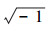
以上证明表明,即使一一对应关系成立,矛盾仍然存在,Cantor的对角线方法也是一样,以下将证明:产生矛盾的根源是不动项xP∈U,而不是那个假设的双射关系。在以上Cantor证明的3个关系,可以总结如下:
1) 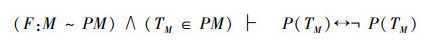
2) 
3) 
在以上Cantor证明的3个关系中,Cantor误认为TM∈PM,Tω∈P(ω),TR∈R都是真命题,这样他误认为证明了以下3个命题:
4) 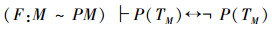
5) 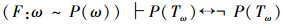
6) 
进而把矛盾产生的根源当成“假设双射关系”引起的,所以,否定双射关系,得到以下结论:
7) 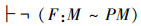
8) 
9) 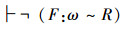
产生矛盾的根源Cantor误认为是(F:M~PM),(F:ω~P(ω)),(F:ω~R)引起的。
所以,Cantor证明的3个关系
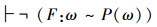

使用正反集合分析,以上证明满足正反集合的条件,正反集合上的不动项,都是U外不动项,产生矛盾的根源实际上是TM∈PM,Tω∈P(ω),TR∈R引起的。所以,在以上推理中,Cantor实际上只证明了以下3个关系:
10) 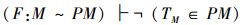
11) 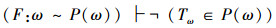
12) 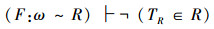
由以上分析可以得到以下推论:
推论13 如果无穷集合演算是一致的,则
推论14 如果自然数集合演算是一致的,则
推论15 如果实数集合演算是一致的,则
注记11 实数不可数”证明错误
1)不动项命题矛盾的存在,不影响集合之间元素的一一对应关系,所以,Cantor对角线法关于无穷集合的幂集不可数证明;自然数的幂集不可数证明;实数不可数的证明都是错误。
2)如果能够构造出实数与自然数的一一映射关系,那么,实数就是一个可数集合,Cantor没有找到这种一一映射关系,并不代表这种对应关系就不存在。前面的证明中,已经知道,不动项TR是一个U外不动项,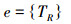
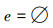
推论16 如果无穷集合、自然数集合、实数集合演算是一致的,则Cantor关于“无穷集合的幂集不可数,自然数的幂集不可数,实数不可数”等命题的证明是错误。
6 递归论中的一些定理的错误证明 6.1 N上存在非递归函数证明错误我们知道,Cantor使用对角线方法,证明“系统N是不完全”的Gödel定理,自然数的幂集合是不可数集合,实数集合是不可数集合。因为“Cantor对角线方法”是数学证明中的一个重要方法,与此相关的重要定理还有“存在非递归集合”、“存在非递归函数”、Tuing机“停机问题”不可判定定理。而对角线方法产生的项是域外不动项,这些定理的证明都是错误的。
定理23 设全部的一元递归函数集合:
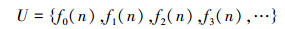
则存在不动项函数h(k),h(k)∉U。
证明 一元函数集合,定义域、值域都是可数集合:
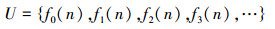
全部函数的枚举如下:
 |
取对角线值的序列,并加1,改为别的值,h(n)=fn(n)+1,
假设h(n)=fn(n)+1,在这个序列之中,得到如下矛盾,h(k)=fk(k)=fk(k)+1。
以上证明是“对角线构造方法”,根据定理,h(k)是不动项函数,h(k)∉U。
根据以上定理,以下推论成立。
推论17 不动项函数h(k)定在U外,h(k)∉U。
推论18 不动项函数h(k)是未定义项。
推论19 不动项函数h(k)是否递归函数,是不可判定命题。
推论20 不动项函数h(k)是否递归函数的不可判定与U内项是否可以判定无关。
推论21 不动项函数h(k)矛盾来源于U外。
推论22 不动项函数h(k)不能作为任何“U内演算的推理依据”。
注记12 ω上存在非递归函数,是“对角线证明方法”,证明错误。
1)递归函数集合是可数的,考察一元递归函数的一个枚举f0,f1,f2,…,定义一个函数
h(k)=fk(k)=g(k,k)+1=fk(k)+1,矛盾,所以,g(m,n)=fm(n)不是递归函数[3]。
2)不存在一元递归函数的能行可枚举,是“对角线证明方法”。
假设存在一元递归函数的能行可枚举,设f0,f1,f2,…,是所有一元递归函数的能行枚举,考察下列算法:给定n∈ω,的枚举f0,f1,f2,…,直到找到fn,计算fn(n)
h(n)=fn(n)+1,n∈ω是递归的,
h(k)=fk(k)=fk(k)+1,矛盾,所以,不存在一元递归函数的能行可枚举[3]。
3)以下定理是“对角线证明方法”,证明错误:
设D(x,y)是一元原始递归函数的通用函数,则D(x,y)不是二元原始递归函数。
证明 D(x,y)是一元原始递归函数的通用函数,所以,全体一元原始递归函数都包含在函数序列D(x,0),D(x,1),D(x,2),D(x,3),…中,可以做以下无穷列表:
| x | y | ||||
| 0 | 1 | 2 | 3 | … | |
| 0 | D(0,0) | D(0,1) | D(0,2) | D(0,3) | … |
| 1 | D(1,0) | D(1,1) | D(1,2) | D(1,3) | … |
| 2 | D(2,0) | D(2,1) | D(2,2) | D(2,3) | … |
| 3 | D(3,0) | D(3,1) | D(3,2) | D(3,3) | … |
| … | … | … | … | … | … |
定义一个一元函数g(x)=D(x,x)+1,如果D(x,y)是二元原始递归函数,g(x)也是一元原始递归函数,设g(x)=D(x,n),n∈ω是递归的,令
x=n,g(n)=D(n,n)
g(n)=D(n,n)=D(n,n)+1,矛盾,所以,D(x,y)
不是二元原始递归函数[6]。
推论23 ω上存在非递归函数的证明错误。
推论24 不存在一元递归函数的能行可枚举,证明错误。
6.2 Turing机“停机问题”证明错误Turing证明,Turing机“停机问题”是不可判定的,即:不存在算法对以下问题类提供答案,{Turing机Tm在输入n后是否会停机| m,n∈N}。
回顾一下图灵机“停机问题”的证明过程。
按照哥德尔编码,给Turing机指定一个编码,按编码的大小,把所有的Turing机一个不漏的枚举如下:T0,T1,T2,…,Tm,…。
定义一个一元函数:
 |
Turing机Tm在输入n后是否会停机的各种情况排列如表 7(表中的所有情况与二进制表示的实数等价)。
| T0 | T1 | T2 | T3 | T4 | … | |
| f(0) | 0 | 1 | 0 | 0 | 1 | … |
| f(1) | 0 | 1 | 0 | 1 | 1 | … |
| f(2) | 0 | 1 | 0 | 1 | 0 | … |
| f(3) | 0 | 0 | 0 | 1 | 0 | … |
| f(4) | 1 | 0 | 0 | 1 | 0 | … |
| … | … | … | … | … | … | … |
假设f(n)是Turing可计算函数,那么存在某个Turing机T来计算f(n)的值,即
对任意n∈ω,f(n)=0⇔T输入n后输出0;f(n)=1⇔T输入n后输出1。
把上表对角线上的元素挑出来。就可以得到一个序列:0,1,0,1,0,…,而根据这个序列完全可以构造这样一个反序列:1,0,1,0,1,…利用反序列,构造一个新的Turing机Tg。
T输入n后输出1⇔Tg输入n后会停机。
Tg是一个新的图灵机,Tg必然出现在T0,T1,T2,…,Tm,…中,设Tg=Tk。
Tk输入k后会停机⇔T输入k后输出1⇔f(k)=1⇔Tk输入k后不停机。
得出矛盾,所以f(n)是Turing不可计算函数。
即:不存在算法对问题类{Turing机Tm在输入n后是否会停机| m,n∈N}提供答案[10]。
以上证明,与“自然数幂集合不可数”,“实数不可数”的证明是一样的。通过分析,可以知道,构造的矛盾是不动项矛盾。
定理24 设U={T0,T1,T2,…,Tm,…},Turing机Tg是不动项。
证明 P是定义在U上的一个性质,命题P是关于正集+α、反集-α的一个二项划分,
P(Tn)⇔Tn在输入n后会停机;
即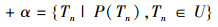

建立映射关系:
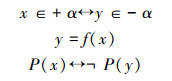 |
当xP满足x=f(x),
以上构造的Tg满足
还可以从“广义U外不动项定理”考虑:
构造项Tg满足以下关系,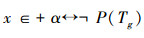

根据“广义U外不动项定理”,Turing机Tg是不动项。
也可以从以下构造的二元项考虑:
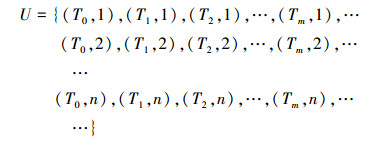 |
U是所有Turing机对所有输入后的状态,这些状态可分为正反两个集合。
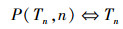

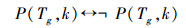
根据U外不动项的一般性质,以下推论成立:
推论25 Turing机不动项Tg一定在U外,Tg∉U。
推论26 Turing机Tg是未定义项。
推论27 Turing机Tg是不可判定命题。
推论28 Turing机Tg的不可判定与U内项是否可以判定无关。
推论29 Turing机Tg矛盾来源于U外。
推论30 Turing机Tg不能作为任何“U内演算的推理依据”。
根据以上推论,Turing机Tg的不可判定与U内项是否可以判定无关,Tg不能作为任何“U内演算的推理依据”,即:Tg矛盾使用“反证法”不成立。故Turing机“停机问题”不可判定证明是错误的。
6.3 一批错误结论及其根源我们知道经典逻辑定理只能在一个封闭的域上使用,由于U外不动项矛盾的存在,“反证法”不能无限制使用。
如果命题P,P(xi)是系统Lα或Kα的一个推论,即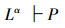

任何一个推理都存在一个已经定义集合:
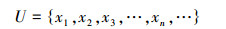 |
在这个集合中使用自指代运算产生悖论是必然的,即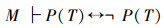
这个悖论不足以否定这个集合内的任何前提,即不能得到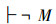
这个悖论只能得到“U上的演算不是封闭的”,即
之所以会产生如此“反证法”错误,因为“项T”原来在U中并没有出现,是在自指代运算中不知不觉就跑出了U的范围,特别是一些高度抽象的项(命题项、函数项),从表面上不能鉴别它是否在U中,只能通过逻辑推理来判断,当“项T”在演算中跑出了U的范围,经典逻辑的定理“反证法”就不成立了,“悖论证明方法、对角线证明方法”就是这种错误。
从经典逻辑封闭性要求看,如果写成:
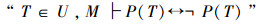
从而得到:
但是,由于“项T”事先并不存在,很难开始就在前提中加入这个条件。
由于经典逻辑的缺陷,Russell、Cantor、Gödel,Turing实际上发现了U外不一致性,发现了U外矛盾不动项,即构造了一个悖论,但是他们没有认识到,他们误以为悖论可以用于“反证法”,证明了“实数不可数”,“不完全定理”,“停机问题不可判定”。
“不动项定理”表明,形形色色排除悖论的努力都是徒劳的,只要有“自指代”,就可能产生悖论。命题逻辑系统L,谓词演算系统K,只要使用“自指代”,同样会有悖论,集合论ZF系统中也没有禁止“自指代”,ZF系统根本防止不了悖论,同样会产生悖论。
“不动项定理”表明,解释清晰后的“悖论”,不但无害,反而有益。无害是因为,悖论是U外项命题,不会对原有的集合U上的演算产生破坏;有益是因为,悖论命题是U外的一种未定义命题,可能是U外的一种新知,这给科学发现指明了一种探求方向。
“不动项定理”还表明,经典逻辑只适用于已经定义的集合,不动项矛盾(悖论)不能作为“反证法”在已定义的集合上的推理依据。可以检查一下,以往的数学证明中,哪些“反证法”证明使用了不动项矛盾,这些证明都是错误的,这里我检查了一些证明,把一些错误的证明结果列表如下:
1)(Gödel不完全定理)如果系统N是ω一致的,那么,存在公式μ不是N的定理,且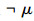
2)任何充分丰富一致的系统,如果系统公理的哥德尔数集合是递归集合,那么它是不完全的。特别地,如果ZF一致的,那么它是不完全的[2]。
3)停机问题是不可判定的,即:不存在算法对以下问题类提供答案:
{Turing机Tm在输入n后是否会停机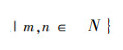
4)不存在所有单变元递归函数的能行枚举[2]。
5)自然数集合上存在非递归集合。
6)自然数集合上存在非递归函数。
7)自然数集合上存在半递归谓词(存在递归可枚举集合)。
8)(Cantor定理)如果PM为M的幂集,且M~PM,则存在T,T⊆M,且T∉PM。无穷集合的幂集不可数[3]。
9)自然数集合与它的幂集合不可能建立一一映射关系。即:自然数集合的幂集不可数[3]。
10)自然数集合与实数集合不可能建立一一映射关系。即:实数集合不可数[3]。
11)对任何集合M,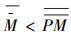
12)(Cantor连续统假设)在
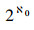
13)(Gödel-Rosser定理) N的任何递归无矛盾扩张N*都不完备。即:如果N*是系统N一致的扩充,并且N*系统公理的哥德尔数集合是递归集合,那么N*是不完全的[4]。
14)设从N可证的公式Gödel数全体构成的集合记为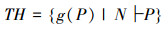
15)所有N中的恒真公式Gödel数全体构成的集合记为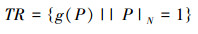
16)(Tarski定理)TR不是算术集合[4]。
…
《数理逻辑》中以此定理为基础的演绎理论都是错误的。
除此以外,以往的数学证明中,还存在大量“反证法”证明使用了不动项矛盾,或者使用对角线证明方法。这值得认真梳理与清理,这将包括哲学、递归论、模型论、证明论、计算机理论、实变函数论等众多科学领域,也许,大家难以相信,这些证明都是错误的。
注 论文(Ⅰ)、(Ⅱ)有大量省略,原稿有更详细论证,需要请与作者联系。
| [1] | 陈汝栋. 不动点理论及应用[M]. 北京: 国防工业出版社, 2012 : 1 -4. |
| [2] | 戴牧民, 陈海燕. 公理集合论导引[M]. 北京: 科学出版社, 2011 : 15 -17. |
| [3] | 张金成. 容纳矛盾的逻辑系统与悖论[J]. 系统智能学报 , 2012, 7 (3) : 208-209 |
| [4] | HAMILTON A G. Logic for Mathematicians[D]. Cambridge: University of Cambridge,1978:29-40,82-92. |
| [5] | 李未. 数理逻辑[M]. 北京: 科学出版社, 2008 : 105 -110. |
| [6] | 张立昂. 可计算性与计算的复杂性[M]. 北京: 北京大学出版社, 2011 : 80 -85. |
| [7] | 克林S C.元数学导论[M].莫绍揆,译.北京:科学出版社,1984:4-12. |
| [8] | 何华灿. 泛逻辑学原理[M]. 北京: 科学出版社, 2001 : 1 -15. |
| [9] | Boolos. 可计算性与数理逻辑[M]. 北京: 电子工业出版社, 2002 : 152 -160. |
| [10] | 汪芳庭. 数理逻辑[M]. 北京: 科学出版社, 2001 : 159 -163. |



