粗糙集理论[1]是由波兰数学家Pawlak于1982年提出的,它是经典集合论的一种推广。这一理论受到数学、计算机与人工智能等方面的研究者的广泛关注。模糊集理论[2]是由Zadeh于1965年建立的,它已成功应用于国民经济的几乎全部领域,之后又被推广到多种广义形式,如直觉模糊集[3]和区间直觉模糊集[4]等。粗糙集和模糊集在处理不确定性和不精确性问题方面都推广了经典集合论,它们都可以用来描述知识的不确定性和不完全性,研究这两种理论之间的关系与融合在理论及应用方面都有重要意义。因此许多学者对此进行了拓展研究,提出了各种广义的粗糙模糊集或模糊粗糙集[5,6],直觉模糊粗糙集和区间直觉模糊(IVIF)粗糙集[7-9]就是其中之一。
1948年,美国工程师Shannon给出了信息度量的数学公式,为研究各种系统不确定性提供了深刻的数学理论与方法。利用Shannon给出的熵公式,Zadeh定义了模糊集合的模糊熵。后来,许多学者提出了多种形式的广义模糊熵度量[10-15]。然而,由于Shannon熵不是一种模糊熵,因此不适合用来度量模糊事件的模糊性。为此,Liang等[16]在Pawlak粗糙集模型中提出了一种新的度量,比较客观地描述了粗糙集中的不确定性问题。
但对区间直觉模糊粗糙集的不确定性度量,目前研究的相对较少,所以本文试图对区间直觉模糊粗糙集的不确定性度量问题进行研究。文献[9]在区间直觉模糊近似空间中,定义了一对区间直觉模糊上、下近似算子,并讨论了算子的一些性质。但由于那里定义的上、下近似算子不具有对称性,因而难以给出其不确定性度量。为此,首先定义新的具有对称性的区间直觉模糊粗糙集模型和区间直觉模糊粗糙集的粗糙隶属函数,然后再利用现有的区间直觉模糊熵公式,给出区间直觉模糊粗糙集的不确定性度量。
1 区间直觉模糊粗糙集的基本理论定义1[4](IVIF集)设U是一个非空经典集合,称U上形如A={〈x,μA(x),υA(x)|x∈U}的三元组为U上的一个IVIF集。
为方便,将IVIF集记为:A={〈x,[μAL(x),μAU(x)],[υAL(x),υAU(x)]x∈U}.
U上所有IVIF集构成的集合为IVIF(U).
定义2 [18]设ai∈[0,1],i∈J,J={1,2,...,m},定义
[a1,b1]=[a2,b2] iff a1=a2,b1=b2;
[a1,b1]≤[a2,b2] iff a1≤a2,b1≤b2;
[a1,b1]〈[a2,b2] iff [a1,b1]≤[a2,b2]且[a1,b1]≠[a2,b2].
定义3 [18]设U是一个非空经典集合,A,B∈IVIF(U),∀x∈U规定序及运算如下:
1)
2)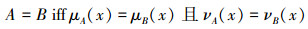
3)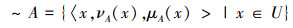
本文均假定U是非空有限论域,且U={x1,x2,…,xn}.
定义4 [19](IVIF关系)设U和W是非空有限论域。定义在直积空间U×W上的IVIF子集为从U到W之间的二元IVIF关系。记为
 |
定义5 设(U,R)是IVIF近似空间,即R是U上的任一IVIF关系。∀A∈IVIF(U),则A在近似空间(U,R)的下近似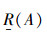
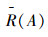
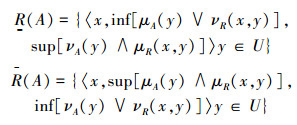 |
(1) |
序对
根据定义5可以直接验证近似算子(1)具有下述性质。
定理1 设(U,R)是IVIF近似空间,对任意的A,B∈IVIF(U),有
1)
2)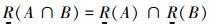
3)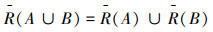
4)
5)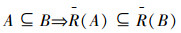
6)
7)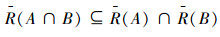
定义6 设(U,R)是IVIF近似空间,对∀A∈IVIF(U),x∈U,x关于A的粗糙隶属函数R(A):IVIF(U)→F(U)定义为
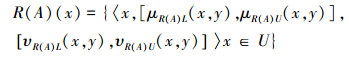 |
式中:
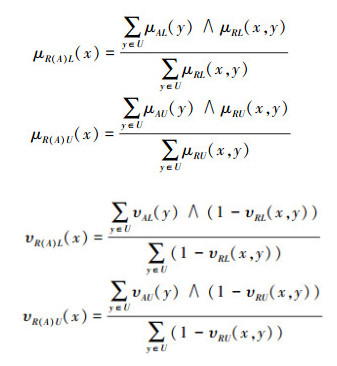 |
(2) |
定理2 设(U,R)是IVIF近似空间,粗糙隶属函数具有性质:
1)∀A,B∈IVIF(U),若A⊆B,则
R(A)⊆R(B)
2)若A∈P(U),则R(~A)=~R(A)。
证明 1)∀A,B∈IVIF(U),若A⊆B,即对∀x∈U有
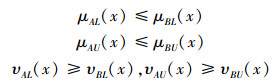 |
则显然有R(A)(x)≤R(B)(x),因此R(A)⊆R(B)。
2)若A∈P(U),则
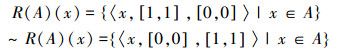 |
又因 ~A=([0,0],[1,1])故 R(~A)(x)={〈x,[0,0],[1,1]〉|x∈A}可得R(~A)=~R(A)。
当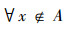

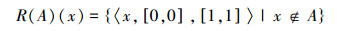
此时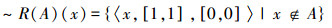
又因
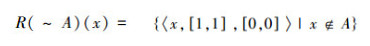
定义7[10] 称映射E:IVIF(U)→[0,1]为区间直觉模糊集的一个区间直觉模糊熵。对∀A∈IVIF(U),如果E满足如下条件:
条件1 E(A)=0,当且仅当A为分明集;
条件2 E(A)=1,当且仅当
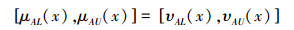 |
条件3 对
条件4 对于任意A,B∈IVIF(U),∀x∈U,当

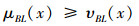
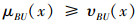
定理3[20] 对
 |
(3) |
则E(A)为A的区间直觉模糊熵。
4 区间直觉模糊粗糙集不确定性度量定义8 设(U,R)是IVIF近似空间,A∈IVIF(U),则IVIF粗糙集
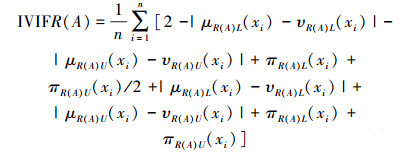 |
(4) |
定理4 设U是非空有限论域,R是U上自反区间直觉模糊关系,即对∀x∈U,有μR(x,x)=[1,1],υR(x,x)=[0,0],A∈IVIF(U),则IVIFR(A)=0当且仅当A是经典集合且是可定义的。
证明 (⇐)设A是经典集合且是可定义的,则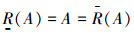
1)对∀x∈A,有


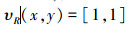
 |
同理可知
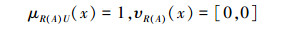 |
2)对

即对∀y∈A,应有υR(x,y)=[1,1],则μR(x,y)=[0,0],所以由式(2)得
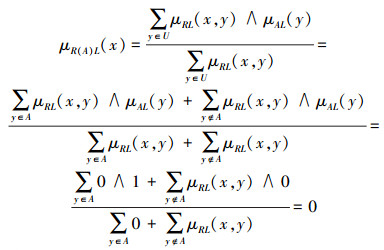 |
同理可得
 |
由1)、2)可知,当A退化为经典集合时:
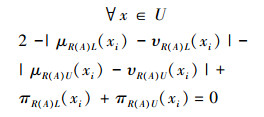 |
故IVIFR(A)=0。
(⇒)设IVIFR(A)=0,由定义8可知,对∀x∈U,应有
 |
亦即
 |
故可得,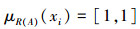
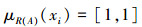
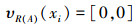
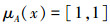
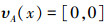
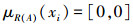
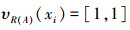
可知,A是经典集合。
由以上证明可知,当IVIFR(A)=0时,A是经典集合。所以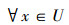
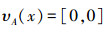
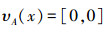
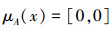
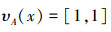
3)若x∈A,即μA(x)=[1,1],υA(x)=[0,0],由式(2)可知:
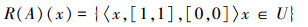 |
则对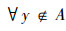


又因为
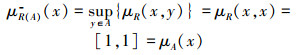 |
于是有
 |
因此,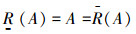
4)若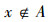
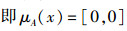
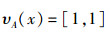
则
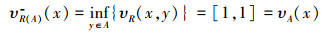 |
于是有
又因为由式(2)可知,R(A)(x)={〈x,[0,0],[1,1]〉x∈U}。
因

从而
因此,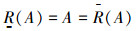
由3)、4)可知,A是可定义的。
定理5 设(U,R)是IVIF近似空间,则A∈P(U),有IVIFR(~A)=IVIFR(A).即
证明 由定理2可知,∀A∈P(U),则R(~A)=~R(A).即
 |
再由定义8的公式直接可得IVIFR(~A)=IVIFR(A).
定理4和定理5说明了什么样的IVIF粗糙集是“确定的”,什么样的集合和它的余集的IVIF粗糙性度量是相等的。
5 结束语区间直觉模糊粗糙集的不确定性不仅来自近似空间,也来自被近似的集合的模糊性。建立一个区间直觉模糊粗糙集模型以后,如何对其不确定性进行度量是一个重要课题。本文通过将区间直觉模糊粗糙集的隶属函数定义为一个区间直觉模糊集,从而可以利用现有文献的区间直觉模糊熵公式,实现了区间直觉模糊粗糙集的不确定性度量,它在不确定性分析方面具有应用价值,值得进一步研究。
| [1] | PAWLAK Z. Rough sets[J]. Theoretional Journal of Computer and Information Sciences , 1982 (11) : 341-356 |
| [2] | ZADEH L A. Fuzzy sets[J]. Information and Control , 1965 (8) : 338-353 |
| [3] | ATANASSOV K. Intuitionistic fuzzy sets[J]. Fuzzy Sets and Systems , 1986, 20 (2) : 87-96 |
| [4] | ATANASSOV K, GARGOV G. Interval-valued intuitionistic fuzzy sets[J]. Fuzzy Sets and Systems , 1989, 31 (3) : 343-349 DOI:10.1016/0165-0114(89)90205-4 |
| [5] | 张文修, 吴伟志, 梁吉业, 等. 粗糙集理论与方法[M]. 北京: 科学出版社, 2001 : 55 -73. |
| [6] | 张文修, 姚一豫, 梁怡. 粗糙集与概念格[M]. 西安: 西安交通大学出版社, 2006 : 61 -84. |
| [7] | ZHANG Z M. An interval-valued rough intuitionistic fuzzy set model[J]. International Journal of General Systems , 2010, 39 (2) : 135-164 DOI:10.1080/03081070903393832 |
| [8] | 张瑜, 王艳平. 直觉模糊粗糙集模型[J]. 辽宁工业大学学报:自然科学版 , 2008, 28 (6) : 414-420 ZHANG Yu, WANG Yanpng. Intuitionistic fuzzy rough sets[J]. Journal of Liaoning University of Technology :Natural Science Edition , 2008, 28 (6) : 414-420 |
| [9] | 王艳平, 孙静, 陈美薇, 区间直觉模糊粗糙集模型[J]. 计算机工程与应用,2011,47 (24):37-42[J]. 辽宁工业大学学报 , 2011, 47 (24) : 37-42 WANG Yanping, SUN Jing, CHEN Meiwei. Interval-valued intuitionistic fuzzy rough sets[J]. Computer Engineering and Applications , 2011, 47 (24) : 37-42 |
| [10] | 魏翠萍, 高志海, 郭婷婷. 一个基于三角函数的直觉模糊熵公式[J]. 控制与决策 , 2012, 27 (4) : 571-574 WEI Cuiping, GAO Zhihai, GUO Tingting. An intuitionistic fuzzy entropy measure based on trigonometric function[J]. Control and Decision , 2012, 27 (4) : 571-574 |
| [11] | BURILLO P, BUSTINCE H. Entropy on intuitionistic fuzzy sets and on interval-valued fuzzy sets[J]. Fuzzy Sets and Systems , 2001, 118 (3) : 305-316 |
| [12] | SZMIDT E, KACPRZYK J. Entropy for intuitionistic fuzzy sets[J]. Fuzzy Sets and Systems , 2001, 118 (3) : 467-477 DOI:10.1016/S0165-0114(98)00402-3 |
| [13] | 郭效之.模糊不确定性度量的探讨及扩展[D].西安:西北大学,2004: 48-50. GUO X Z. The discussion and extension of fuzzy uncertainty measure[D]. Xi′an: northwestern university,2004: 48-50. |
| [14] | 屈克, 汤磊, 荣文静. 区间直觉模糊集熵的构造及其基本性质[J]. 重庆文理学院学报:自然科学版 , 2010, 29 (3) : 21-24 QU K, TANG L, RONG W J. The construction and basic properties of entropy of interval-valued intuitionistic fuzzy sets[J]. Journal of Chongqing University of Arts and Sciences : Natural Science Edition , 2010, 29 (3) : 21-24 |
| [15] | YE J. Two effective measures of intuitionstic fuzzy entropy[J]. Computing , 2010, 87 (1/2) : 55-62 |
| [16] | LIANG J Y, CHIN K S, DANG C Y, et al. A new method for measuring uncertainty and fuzziness in rough set theory[J]. International Journal of General Systems , 2002, 31 (4) : 331-342 DOI:10.1080/0308107021000013635 |
| [17] | ATANASSOVK. Operators over interval valued intuitionistic fuzzy sets[J]. Fuzzy Sets and Systems , 1994, 64 : 159-174 |
| [18] | GONG Z T, SUN B Z, CHEN D G. Rough set theory for interval-valued fuzzy information systems[J]. Information Sciences , 2008, 178 : 1968-1985 DOI:10.1016/j.ins.2007.12.005 |
| [19] | 彭振文, 王周敏. 区间直觉模糊关系及其性质[J]. 海南师范大学学报:自然科学版 , 2008, 21 (4) : 412-415 PENG Z W, WANG Z J. The Interval-valued intuitionistic fuzzy relations and their properties[J]. Journal of Hainan Normal University : Natural Science Edition , 2008, 21 (4) : 412-415 |
| [20] | 王培, 魏翠萍. 一种区间直觉模糊熵的构造方法[J]. 计算机工程与应用 , 2011, 47 (2) : 43-45 WANG P, WEI C P. Constructing method of interval-valued intuitionistic fuzzy entropy[J]. Computer Engineering and Applications , 2011, 47 (2) : 43-45 |



