线性二次最优控制(linearquadraticregulator,LQR)[1]在现在的控制理论中是一种非常重要的最优控制算法,这主要是由于LQR是其他控制方法的基础并且能够很容易地应用到工程控制问题中。目前,LQR控制方法已经广泛应用于异步电动机控制、车辆驱动轴控制和结构振动控制等方面。
在实际应用中,在进行LQR控制器的设计时,关键问题是对权矩阵Q和R的调整,Q和R的选取往往和所设计的控制器有关,并且没有好的方法确定Q和R。设计者往往凭经验采用多次试探法来确定一种相对较好的Q和R,但是,试探法往往得到的是局部最优控制方法。为此,Kalman首先提出一种加权矩阵选择法[2]。文献[3]对加权矩阵选择法进行了进一步的改进。近年来,研究者采用遗传算法[4-7]、粒子群算法[8]和蚁群算法[9]等群智能算法进行LQR控制器的优化并取得不错效果。但是,还是存在优化用时长、获得全局最优解成功率低等问题[10-11],本文提出一种改进的教与学优化算法进行LQR控制器的优化。
1 LQR控制算法假设受控线性不变系统的状态方程模型为
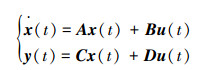 |
(1) |
式中:x(t)是状态向量,u(t)是控制向量,y(t)是输出向量,A是系数矩阵,B是输入矩阵,C是输出矩阵,D是传递矩阵。
定义控制系统的二次型性能泛函为
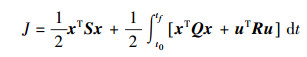 |
(2) |
式中:Q为状态变量的加权矩阵,是半正定矩阵;R为输入变量的加权矩阵,是正定矩阵。
该系统最优控制的目标是寻求最优控制u(t),使得系统趋近于初始化状态,并使J取得最小值。由线性二次型最优控制理论可知,如果要使得J最小,则控制向量应该为
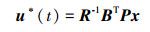 |
(3) |
式中:P为对称矩阵,该矩阵满足:
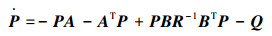 |
(4) |
考虑在稳态的情况下,系统状态逐渐趋近于0,可将式(4)简化为Riccati代数方程:
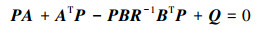 |
(5) |
显然,上述最优控制系统的性能指标主要取决于对称矩阵P,而P主要由矩阵A、B、Q和R确定。A和B是参数矩阵,因此,系统性能主要由矩阵Q和R来决定。然而,Q和R怎样选取没有具体的求解方法,常常依赖于设计者的主观经验进行实验调整,直至获得相对可接受的满意解。
本文采用一种新型改进快速智能优化算法进行LQR控制器的优化设计。通过汽车主动悬架作为被控对象,将提出的一种新的“教与学”优化算法应用于LQR控制器的设计中,并将结果与遗传算法、粒子群优化算法和标准的“教与学”优化算法在LQR控制器优化中的性能进行比较。
2 教与学优化算法“教与学”优化(TLBO)算法[12-18]是一种新型的群体智能优化算法,通过模拟人类的学习过程:“教”和“学”。通过两个阶段的学习,从而促进每个个体的学习水平。
在标准的TLBO算法中,“班级”是个体的集合,每个个体相当于一个学员,每个学员所学的某一科目相当于一个决策变量。水平最高的学员被称为“教师”。每个学员通过“教师”的“教”和向其他学员“学习”来提高自身水平。
1)“教”阶段。
在“教”阶段,班级中每个学员Xj(j=1,2,…,NP)根据Xteacher和班级中学员平均水平值 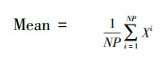
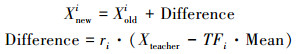 |
式中: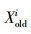
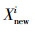
2)“学”阶段
在“学”阶段,学员Xi(i=1,2,…,NP)从班级中随机选取一个学员Xj(j=1,2,…,NP,j≠i)作为学习对象,Xi分析和比较自己和学员Xj之间的差异,然后进行学习。学习过程如下:
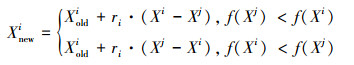 |
式中,ri=U(0,1)表示第i个学员的学习因子(学习步长)。
3)学习结果更新,学员在经过学习后要进行更新操作。更新方法如下:
 |
基本TLBO算法的流程如图1所示。
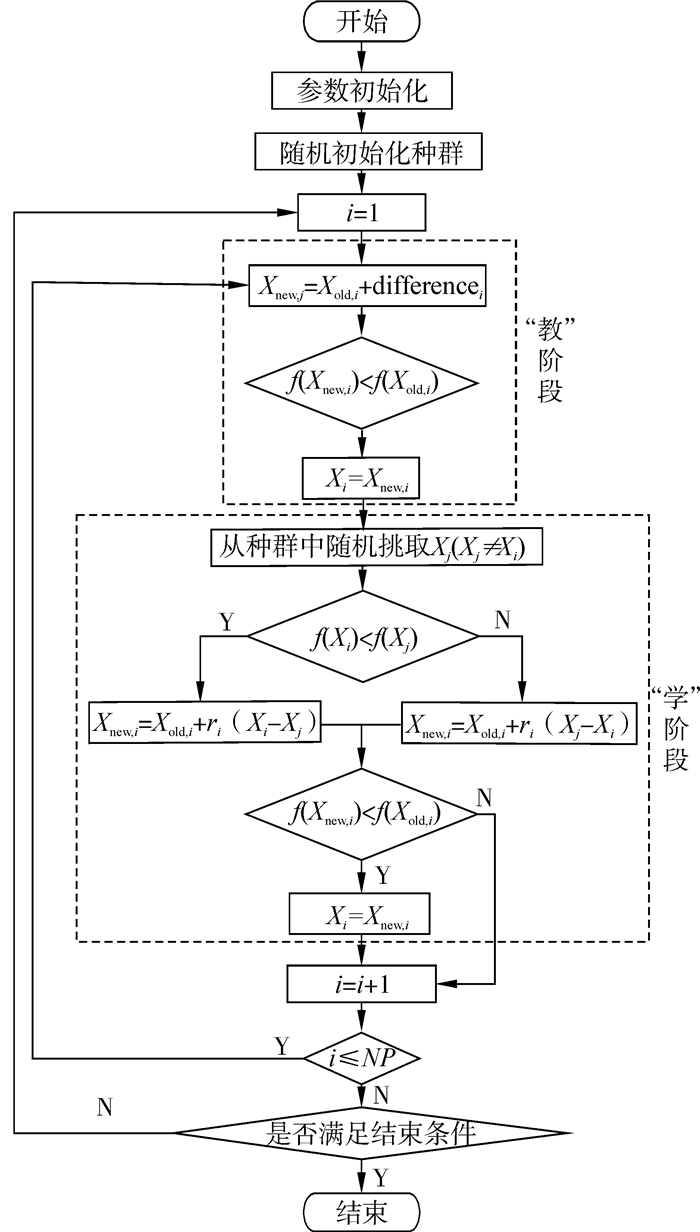
|
| 图 1 TLBO算法流程图 Fig. 1 Flow chart of TLBO algorithm |
在标准的TLBO算法中,所有学员的的水平提高,完全依赖老师的“教”和学员之间的交流“学习”,从而使得学员在学习过程中对他人的过度依赖。我们知道,每个人的学习主要是靠自身的努力和探索,个人的创新能力是最重要的[19-20]。因此,为了发挥群体中每个学员的创新能力,本文提出一种具有自我学习能力的教与学优化算法(motifiedteaching-learning-basedoptimization,MTLBO),算法借鉴和声搜索算法思想进行个体的自我学习和自我探索创新能力挖掘,用于加强每个个体的局部搜索能力,从而增强种群的全局最优解的求解能力。
3.1 “教”(Teaching)学阶段的改进本文中对Mean进行改进,使的原来的Mean=(Xworst+Xi)/2,这样计算的好处是每个个体Xi在教学过程中Mean值都不同,从而保证种群的多样性,避免算法过早收敛,具体如下:
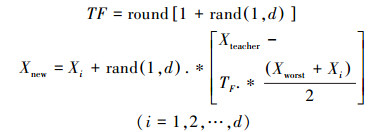 |
TLBO算法在相互“学习”阶段,每个学员Xi(i=1,2,…,N)每次学习时随机选取一个学习对象Xj(j=1,2,…,N,j≠i)进行学习,学习较为单一。本文算法要求每个学员在进行“相互学习”是,每次从班级中随机选取2个学习对象Xr1和Xr2(r1=1,2,…,N;r2=1,2,…,N;r1≠r2)进行学习,学习过程伪代码如下:
 |
rand(1,d)表示在[0,1]区间随机生成一个d维的行向量。
3.3 “自我”学习(self-learning)阶段本文算法提出一种类似于和声搜索算法的自我学习策略。每个个体通过自我调整进行优化学习。由于每个学员可能同时学习多门课程(多个决策变量),在进行“自我”学习时只是对部分科目进行调整学习,保持优势学科,增强劣势科目。采用3种自我调整策略进行学习:
1)向“某一科”较为优秀的同学学习,增强单科水平。学习概率为LoP。
2)自我调整,以概率SRP进行科目调整,调整步长为Step。
3)以概率ILP进行创新学习。
“自我”学习阶段的具体算法如下:
 |
其中,
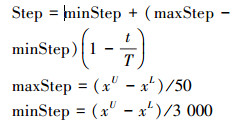 |
t是当且迭代次数,T是允许最大迭代次数。
4 MTLBO算法主动悬架LQR控制器优化 4.1 车辆主动悬架LQR控制器模型本文以单轮车辆模型作为研究对象,如图2。具体系统运动方程和状态方程请参阅文献[11-21]。图2中,xb表示车身垂向位移,xg表示路面垂向位移,xw表示车轮垂向位移,Ks表示悬架刚度,Kt表示车胎刚度,Ua表示控制力。

|
| 图 2 单轮车辆控制模型 Fig. 2 Control model of single wheel vehicle |
LQR控制器的性能评价指标为 
 |
式中:mb是簧载质量。
最优控制力Ua=-Kx(t),其中,K是反馈增益矩阵,通过调用MATLAB中的线性二次最优控制设计函数LQR(A,B,Q,R,N)可得到。
由于,该控制器的最优控制性能主要决定于加权系数为X(q1,q2,q3),本文采用改进的教与学优化(MTLBO)算法进行优化。根据车辆主动悬架的性能评价指标:车身垂直加速度BA,悬挂动行程SWS和轮胎动位移DTD。因此,可将控制问题可表示为多目标优化问题[10]:
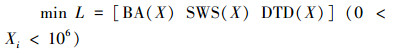 |
本文将其转化为单目标优化问题:
 |
式中:α、β、γ表示3个目标的权重(α+β+γ=1)。BApas、SWSpas和DTDpas表示3个目标的在被动悬架的性能。这样转换的目的是更公平的对3个目标进行优化。单轮车辆主动悬架LQR控制模型的Simulink图形如图3。
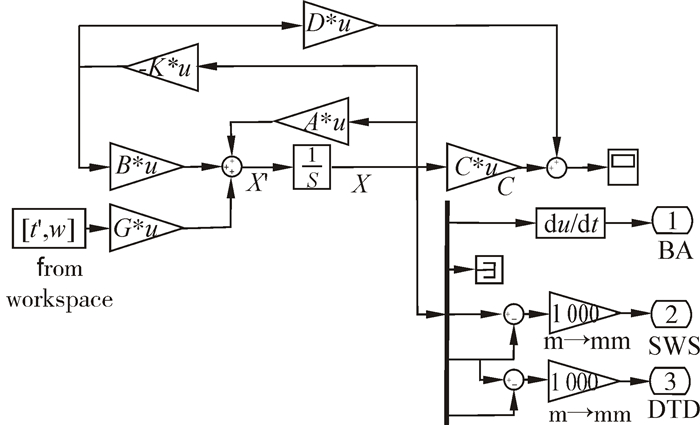
|
| 图 3 主动悬架LQR控制模型 Fig. 3 LQR control model of active suspension |
采用改进的教与学算法进行LQR控制器优化算法流程如下:1)参数初始化。2)在可行域随机产生班级学员。3)根据LQR控制器输出反馈增益矩阵K,运行主动悬架模型,计算每个学员的适应值。4)选定老师,对每个学员进行“教”后,根据第5)步重新计算学员的适应值,如果有进步则更新。5)学员之间相互学习,重新计算适应值并更新。6)自我学习调整。7)是否满足终止条件,如果满足则结束,否则转至4)继续。算法具体流程如图4所示。

|
| 图 4 MTLBO算法流程图 Fig. 4 Flow chart of MTLBO algorithm |
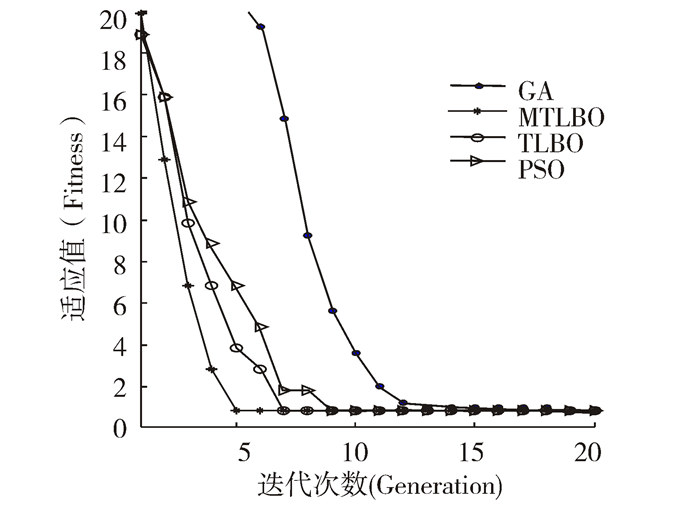
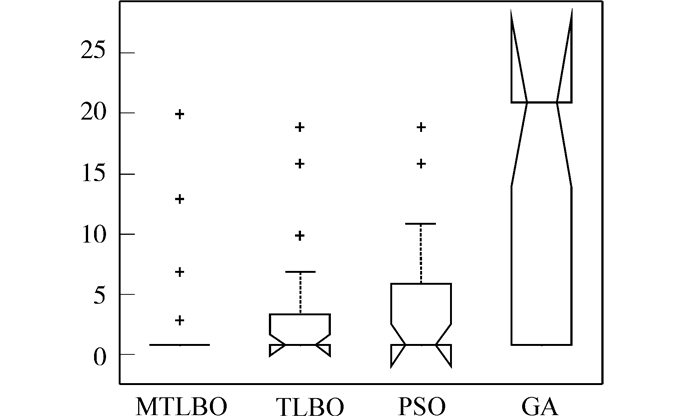
为测试算法性能,将其和基本TLBO算法、粒子群优化(PSO)算法和遗传算法进行比较。在测试中,主动悬架参数设置和文献[11]中一致:mb=320kg,mw=40kg,Ks=20000N/m,G0=5×10-6m3/cycle.参数α=0.35,β=0.25,γ=0.4。使用微机硬件环境为戴尔工作站:IntelXeon(R)2.4GHzCPU,8GB内存;软件是在MATLAB2009(a)软件平台上进行编程实现。各种优化算法参数设置如表1。对每种算法都进行20次独立运行,记录了运行所获的最优解、最差解,并计算出20个最优解的平均值和标准差,结果如表2。图5中绘制了4种算法在20次运行中的平均优化曲线,图6采用盒图统计了20次实验的最优解分布.由图5可以看出,本文算法(MTLBO)的收敛速度最快且求解精度最高。图6显示,本文算法在20次运行中最为稳定,并且平均最优解最小。说明本文算法具有收敛速度快、求解精度高和稳定性好等优势。
| 算法 | 允许最大迭代次数 | 种群大小(NP) | 其他参数 |
| PSO | 40 | 20 | w=0.6,c1=c2=2;Vmax=1,Vmin=-1 |
| GA | 100 | 100 | 交叉概率cp=0.4;精英个数为10,采用分散交叉函数 |
| TLBO | 20 | 20 | — |
| MTLBO | 20 | 20 | TOP=0.55,SRP=0.3,ILP=0.1 |
| 算法 | Best | mean | Worst | Std |
| MTLBO | 0.855229 | 0.855229 | 0.855237 | 1.93E-06 |
| TLBO | 0.85523 | 0.855241 | 0.855272 | 1.2E-05 |
| PSO | 0.855229 | 0.855237 | 0.855298 | 1.65E-05 |
| GA | 0.856105 | 13.8722 | 20.90828 | 9.545736 |
| 算法 | 性能指标 | 目标函数 适应值 |
q1 | q2 | q3 | ||
| 车身加速度 BA/(m·s-2) |
悬挂动行程 SWS/mm |
车胎动位移 DTD/mm |
|||||
| 被动悬架 | 6.2526 | 1.7816 | 17.1284 | — | |||
| MTLBO | 5.53696 | 1.7035 | 12.025 | 0.85522 | 102204.44306 | 11672.867716 | 208888.16755 |
| TLBO | 5.53760 | 1.7017 | 12.0534 | 0.8552 | 98951.349826 | 11948.859186 | 138294.09773 |
| PSO | 5.56520 | 1.6864 | 12.1408 | 0.8552 | 96559.031114 | 12161.725204 | 1000000 |
| GA | 5.46775 | 1.7203 | 12.0725 | 0.8554 | 117683.10992 | 10323.858400 | 992496.42946 |
|
| 图 5 4种算法的优化过程曲线 Fig. 5 The convergent curves of four algorithms |
|
| 图 6 20次独立运行中4种算法的最优解分布 Fig. 6 Distribution of the optimal solutions of four al-gorithms after 20 independent runs |
通过分析LQR控制器加权系数选择较难这一问题,给出了优化设计的基本思路。并提出一种改进的教与学优化算法(MTLBO),该算法模拟人类学习的基本过程(老师教、学生之间相互学和自学)进行设计。文中将改进的算法用于单轮车辆模型作为研究对象,建立主动悬架评价模型,采用MTLBO算法进行LQR控制器的优化,通过仿真实验证明本文算法在LQR控制优化方面是有效可行的。
| [1] | RAO P, CROW M L, YANG Z. STATCOM control for pow-er system voltage control applications[J]. IEEE Trans Power Electron , 2000, 15 (4) : 1315-1317 |
| [2] | KALMAN R E. When is a linear control system optimal[J]. J Basci Eng Trans , 1964, 86 (1) : 51-56 DOI:10.1115/1.3653115 |
| [3] | WANG Yaoqing. The determination of weighting matrices in LQ optimal control system[J]. Acta Automatic Sinica , 1992 |
| [4] | SUNG Gheng chung,CHEN Gong.Optimal control systems design associated with genetic algorithm[C]//Proceedings of 2006 CACS Automatic Control Conference St. Taiwan, China, 2006: 10-11. |
| [5] | BOTTURA C P.Rule based decision making unit for Eigen structure assignment via parallel genetic algorithm and LQR design[C]//Proceedings of the American Control Confer-ence. Chicago, Illinois, 2000: 467-471. |
| [6] | BOTTURA C P. Parallel eigen structure assignment via LQR design and genetic algorithms[C]//Proceedings of the American Control Conference. San Diego, 1999: 2295-2299. |
| [7] | HASSANZADEH I, MOBAYEN S, HARIFI A. Input-output feedback linearization cascade controller using genetic algo-rithm for rotary inverted pendulum[J]. American Journal of Applied Sciences , 2008, 5 (10) : 1322-1328 DOI:10.3844/ajassp.2008.1322.1328 |
| [8] | HAMIDI J. Control system design using particle swarm opti-mization[J]. International Journal of Soft Computing and En-gineering , 2012, 1 (6) : 2231-2307 |
| [9] | 刘璐, 任开春, 武明亮. 基于网格划分策略的自适应ACO算法优化LQR控制器权值[J]. 西南科技大学学报 , 2012, 25 (3) : 82-88 LIU Lu, REN Kaichun, WU Mingliang. LQR Controller weight matrices optimized by adaptive ant colony algorithms based on meshing strategy[J]. Journal of Southwest Univer-sity of Science and Technology , 2012, 25 (3) : 82-88 |
| [10] | 史峰, 王辉. MATLAB智能算法30个案例分析[M]. 北京: 北京航空航天大学出版社, 2011 : 255 -300. |
| [11] | 郭一峰, 徐赵东, 涂青, 等. 基于遗传算法的LQR算法中权矩阵的优化分析[J]. 振动与冲击 , 2010, 29 (11) : 217-221 GUO Yifeng, XU Zhaodong, TU Qing, et al. Optimized a-nalysis of weight matrix in LQR algorithm based on genetic algorithm[J]. Journal of Vibration and Shock , 2010, 29 (11) : 217-221 |
| [12] | RAO R V, SAVSANI V J, VAKHARIA D P. Teaching-learning-based optimization: anovel method for constrained mechanical design optimization problems[J]. Computer-Aided Design , 2011 |
| [13] | RAO R V, SAVSANI V J, VAKHARIA D P. Teaching-learning-based optimization: an optimization method for continuous non-linear large scale problems[J]. Information Sciences , 2012 : 1-15 |
| [14] | 拓守恒, 雍龙泉, 邓方安. "教与学"优化算法研究综述[J]. 计算机应用研究 , 2013 (7) : 1933-1938 TUO Shouheng, YONG Longquan, DENG Fang'an. Survey of teaching-learning-based optimization algorithms[J]. Ap-plication Research of Computers , 2013 (7) : 1933-1938 |
| [15] | 何红, 拓守恒. 教与学优化算法在梯级水库优化调度中的应用[J]. 计算机与数字工程 , 2013, 7 (7) : 1057-1059 HE Hong, TUO Shouheng. Application of teaching-learning-based optimization in optimal dispatching of cascade reservoirs[J]. Computer &Digital Engineering , 2013, 7 (7) : 1057-1059 |
| [16] | 拓守恒. 一种优化神经网络的教与学优化算法[J]. 智能系统学报 , 2013, 8 (4) : 327-332 TUO Shouheng. A modified teaching-learning-based optimization algorithm and application in neural networks[J]. CAAI Transactions on intelligent systems , 2013, 8 (4) : 327-332 |
| [17] | 拓守恒. 改进的教与学优化算法[C]//第32届中国控制会议论文集(E卷). 西安, 中国, 2013: 7976-7981. TUO Shouheng. Modified teaching-learning-based optimiza tion algorithm[C]//2013 32nd Chinese Control Conference, Xi′an, China, 2013: 7976-7981. |
| [18] | 拓守恒. 利用教与学优化策略改进的和声搜索算法[C]//第32届中国控制会议论文集(E卷). 西安, 中国, 2013: 6-10. TUO Shouheng. An improved harmony search algorithm based on teaching-learning strategy[C]. 2013 32nd Chinese Control Conference, 2013: 6-10. |
| [19] | EK M C, LIU S H, MERNIK L. A note on teaching-learning-based optimization algorithm[J]. Information Sciences , 2012 : 79-93 |
| [20] | RAO R V, PATEL V. An elitist teaching-learning-based optimization algorithm for solving complex constrained opti-mization problems[J]. International Journal of Industrial Engineering Computations , 2012 (3) : 535-560 |
| [21] | 胡斐, 赵治国. 主动悬架LQR控制加权系数多目标遗传算法优化[J]. 机械与电子 , 2011 (2) : 28-31 HU Fei, ZHAO Zhiguo. Optimization of weighting factors for LQR controller of active suspension based on multi-ob-jective genetic algorithm[J]. Machinery & Electronics , 2011 (2) : 28-31 |



