云模型是我国学者李德毅教授在结合概率论和模糊数学理论的基础上,通过赋予样本点随机确定度来统一刻画概念中的随机性、模糊性及其相互关联性。[1]它利用期望、熵、超熵3个数字特征描述一个定性概念,通过相应的算法形成用数字特征表示的定性概念与其相对应的定量表示之间的不确定性转化模型,主要体现了这一概念的随机性与模糊性,并把二者完全集中在一起,构成定性概念(概念内涵)和定量数据(概念外延)相互转换,深刻揭示了客观现象具有的随机性和模糊性[2]。
在云理论中,正向云发生器是由特定的算法实现概念的内涵向其外延的转换,就是由定性概念的数字特征生成一定数量的数据。由于逆向云生成算法是把一定数量的样本数据转换成数字特征表示的定性概念,也就是一个定性概念数字特征的还原[3-6]。在这一个过程中误差是不可避免的,因此算法的关键是构造一个相对准确的逆向云发生器。其中文献[7]中提出了基本的逆向云发生器,但这种算法的误差较大[7]。罗自强等提出了曲线拟合的逆向云发生器,结果的精度有所提高,但是拟合初值的选取影响结果的稳定性[8]。本文针对曲线拟合逆向云算法中参数不规律跳变、误差较大的现象,提出了一种优化设计方案,并通过仿真验证其有效性。
1 云模型理论设U是一个用精确数值表示的定量论域,C是U上的定性概念,若定量值x∈U,且x是定性概念C的一次随机实现,x对C的确定度μ(x)∈[0, 1]是有稳定倾向的随机数,则x在论域U上的分布称为云,每一个x称为一个云滴。
云模型的数字特征:期望Ex、熵En和超熵He,这3个数字反映了定性概念的定量特征。
期望Ex:最能够表示定性概念的某些点。与Ex距离越近,云滴集中性越好,反映人们对定性概念的认知比较统一;与Ex距离越远,云滴相对分散,反映人们对概念认知越不稳定,不统一。
熵En:定性概念不确定性的度量。En表达定性概念的亦此亦彼性,反映了云滴在论域空间被接受的区域范围,也就是模糊度量;En还反映云滴出现的随机性,代表云滴的离散度;同时熵也反映模糊性和随机性之间关联性。一般来说,熵的取值越大,表示概念越宏观,模糊性和随机性也就越大,对概念的确定性表达就比较困难。
超熵He:定性概念熵的不确定性表示,即熵的熵。由熵的模糊性和随机性共同决定。
由以上定义可知,论域中的值表示的定性概念的确定度不是恒定不变的,而是在细小变化着的。但这种细小的变化并不影响云模型的整体特征,对云来说,重点在于研究云的整体形状反映出的不确定性概念的特征,以及云滴大量出现时确定度值呈现的规律性[9-10]。
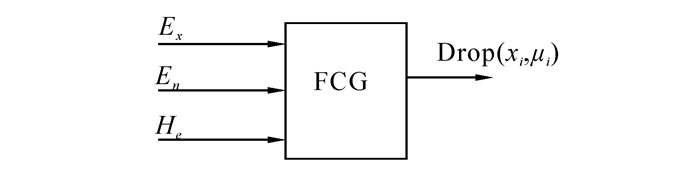
云模型中最重要的算法是正向云发生器和逆向云发生器。由数字特征C(Ex, En, He)生成特定定量数据的算法,称为正向云发生器(forward cloud generator),用FCG表示,如图 1。云模型既不是一条清晰的隶属度曲线,也不是一个确定的概率密度函数。而云模型是由两次串接的正态发生器生成的许多云滴所组成,不仅是一对多的泛正态数学映射图像,而且是一朵可以伸缩、无确定边缘的云图,并具有定量和定性之间的转换的功能。
|
| 图 1 正向云发生器 Fig. 1 Forward cloud generator |
正向云发生器的算法描述如下。
输入:定性概念A~的数字特征Ex, En, He以及云滴个数N。
输出:N个云滴的定量数值和云滴的确定度。
算法步骤:
1)以En为期望,He为标准差生成一正态随机数En′;
2)以期望为Ex,标准差为En′生成一正态随机数x;
3)计算: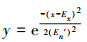
4)x就称为一个云滴,表达定性概念A~的一次具体量化;y称作x属于定性概念A~的确定度;
5)重复1)~4),直至生成N个云滴。
逆向云发生器将一定量的样本转换为用数字特征表示的定性概念,也就是一个定性概念数字特征的还原过程,在这个过程中不可避免地会有误差产生,因此人类认知过程的关键在于构造一个相对准确的逆向云发生器[11-13]。
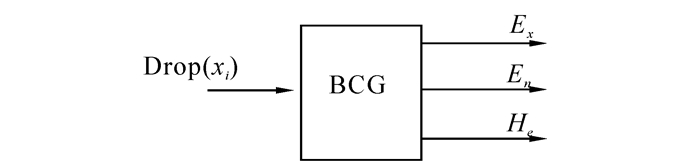
2 基于曲线拟合的逆向云改进算法逆向云发生器(backward cloud generator,BCG)是从定量到定性的映射,它将一定数量的精确数值有效转换为以数字特征C(Ex, En, He)表示的定性概念,实现定量数值与定性概念之间不确定性的转换和定性概念的外延到内涵转换的过程。逆向云发生器如图 2所示。
|
| 图 2 逆向云发生器 Fig. 2 Backward cloud generator |
依据统计原理,如果给定的样本点越多,则逆向云算法得到的参数估计误差越小。无论采用什么算法,在样本点数量有限的情况下,误差不可避免。
下面讨论正态云(X, Y)的期望特性曲线。
当xi是一维时,正态云(X, Y)是二维随机变量,其联合概率密度函数为
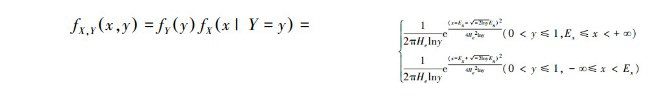 |
由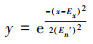
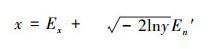
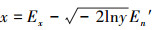
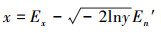
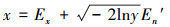
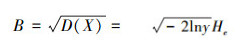
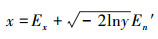
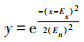
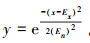
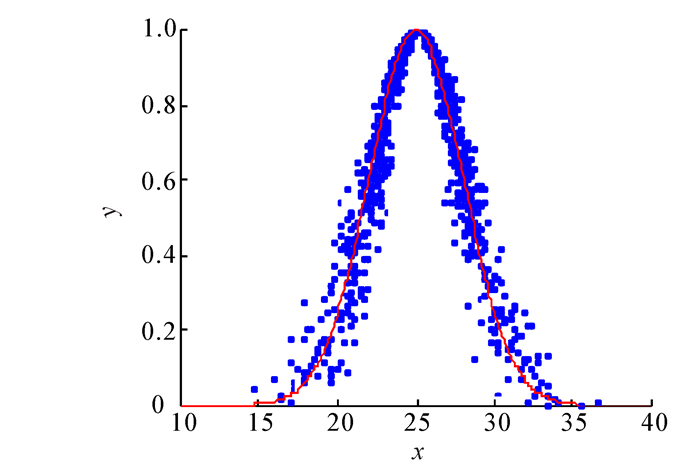
正态云期望曲线如图 3所示,其几何形状具有明显的特点,反映了正态云模型的理想曲线。期望曲线用来表示数据集合在空间分布的统计规律。期望曲线是一条光滑、连续的曲线,刻画了云模型的整体特性, 是云滴的总体轮廓。He反映了所有云滴围绕期望曲线做随机波动的程度。这里的总体轮廓不是几何意义下的中间部分,而是概率意义下的期望。
|
| 图 3 正态云模型的期望曲线 Fig. 3 Expectation curve of normal cloud model |
图 3中离散的点表示云滴,光滑曲线表示的是云模型的期望曲线。
在基本逆向云生成算法中,N个云滴的定量值x1, x2, …xi(i=0~N)作为输入,输出为定性概念A~的期望,熵以及超熵的估计值Êx、Ên、Ĥe。首先计算这些数据的均值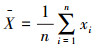
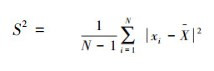
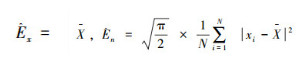
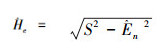
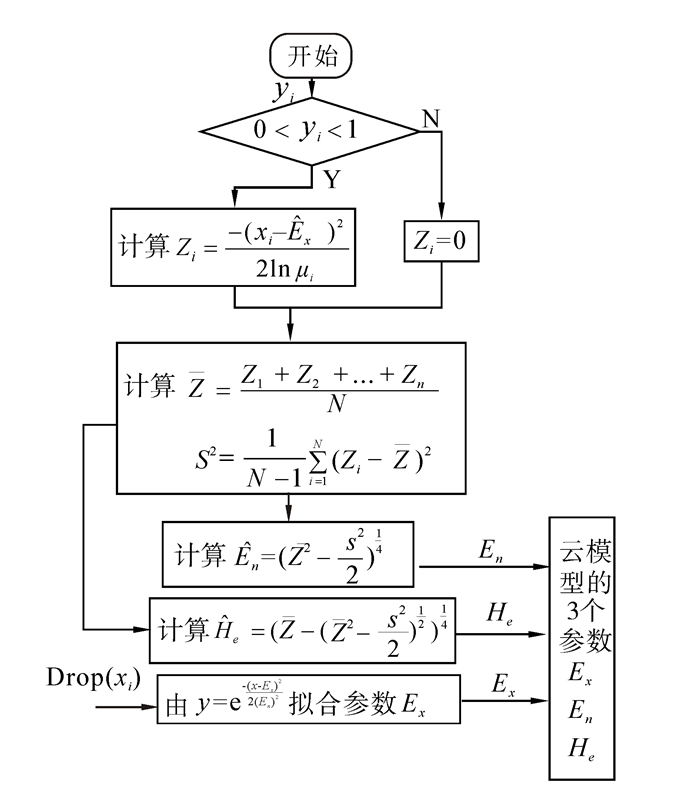
基本逆向云算法会产生较大的误差。基于曲线拟合的逆向云生成算法如图 4所示。从流程图可知曲线拟合的初始值在选取的时候是随机选取的,这样会造成结果的不稳定。针对这一问题,考虑优化拟合参数的初值对算法进行改进[14]。
|
| 图 4 曲线拟合逆向云算法流程图 Fig. 4 The flowchart of curve fiting backward cloud algorithm |
根据正态云模型的期望曲线编写M函数文件“ni”。
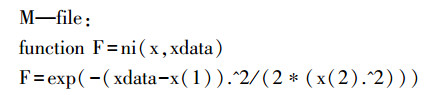 |
利用非线性数据拟合函数lsqcurvefit进行曲线拟合。[x, resnorm]=lsqcurvefit(@ni, x0, xdata, ydata)
其中:ni为拟合的M函数文件名,x0为初始向量,xdata、ydata为曲线拟合的实验数据。在实际应用中,x0的选取对实验结果的影响比较大,在此算法中把xdata的均值作为拟合的初始值进行拟合。函数返回值[x, resnorm]为非线性函数“ni”的拟合系数,即期望和熵。改进后的算法输入为N个云滴的定量值x1, x2, …, xi(i=0~N)以及每个云滴的确定度,输出为定性概念A~的期望Ex、熵En和超熵He的估计值Êx、Ên、Ĥe[15]。
1)根据xi计算这组数据的样本均值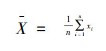
2)用X作为拟合曲线方程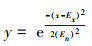
3)若0 < μi < 1,计算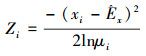
4)计算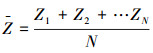
5)计算He的估计值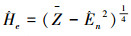
MATLAB实现关键代码如下:
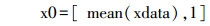 ;
; |
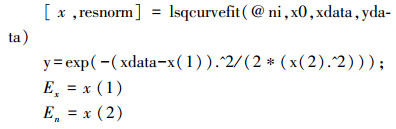 |
将上述的3种逆向云生成算法利用MATLAB进行仿真。选取的3个参数为Ex=25,En=3,He=0.1,先由正向云生成算法生成云滴,云滴数由1000开始,一次增加2 000,原曲线拟合逆向云生成算法中选取拟合初值x0=[1,1]进行拟合,改进的曲线拟合逆向云生成算法中用x0=[mean(xdata), 1]作为拟合初值进行曲线拟合。实验仿真结果对比如表 1~3所示。
| 云滴数 | 基本逆向云 | 曲线拟合 | 改进曲线拟合 |
| 1000 | 24.9281 | 24.0030 | 24.9968 |
| 3000 | 25.0329 | -73.5728 | 25.0003 |
| 5000 | 24.9881 | 24.9989 | 25.0012 |
| 7000 | 25.0078 | -383.2262 | 24.9999 |
| 9000 | 25.0022 | 25.0021 | 25.0008 |
| 10000 | 25.0017 | 25.0000 | 25.0000 |
由表 1可知随着云滴数的增加,期望Ex的值越来越接近实际值。由统计学理论知,样本点数给定的愈多,逆向云生成算法得到的参数估计误差就愈小。在样本点有限的情况下,无论采用什么算法,误差都是不可避免的。但是曲线拟合逆向云生成算法中期望Ex的值明显比基本的逆向云生成算法的期望值要精确,但出现了结果远远偏离实际值的不稳定现象。由此可知,在曲线拟合的过程中初值的选取是非常关键的,初值选取不当会造成较大的误差,且结果很不稳定。而改进的算法中结果相对来说比较稳定,精度也比基本的逆向云生成算法高。基本逆向云算法中只利用N个样本值,而没有考虑样本发生的概率,以此参数的估计值误差相对于改进算法要大至少一个数量级。
由表 2知,这3种逆向云生成算法中,原逆向云生成算法中熵的结果相对比较稳定,但是精度不是很高。曲线拟合算法中也出现了超熵远远大于其他值的现象,结果很不稳定。在改进的逆向云生成算法中精度较高,每一次的实现结果相差不大,在千分之一范围内变化。可见期望值的精度很大程度上影响了熵的精度,因此得到一个相对精确的期望值对熵的计算值有较大的提高。
| 云滴数 | 基本逆向云 | 曲线拟合 | 改进曲线拟合 |
| 1000 | 2.9872 | 3.0014 | 3.0089 |
| 3000 | 2.9814 | 118.5922 | 3.0036 |
| 5000 | 3.0410 | 2.9988 | 3.0019 |
| 7000 | 2.9419 | 495.3311 | 3.0003 |
| 9000 | 2.9566 | 3.0001 | 3.0008 |
| 10000 | 3.0092 | 2.9973 | 3.0011 |
由表 3可以看出,基本的逆向云生成算法中超熵He的值与实际值相比有比较大的出入,而且实验的波动性比较大。曲线拟合逆向云生成算法中的有些值比较接近实际值,但是不稳定,出现较大误差的现象,改进的曲线拟合逆向云生成算法的结果稳定性比较好,而且接近实际值,效果比较理想。
| 云滴数 | 基本逆向云 | 曲线拟合 | 改进曲线拟合 |
| 1000 | 0.5431 | 0.0986 | 0.1018 |
| 3000 | 0.2759 | 648.5920 | 0.1026 |
| 5000 | 0.2068 | 0.1008 | 0.1009 |
| 7000 | 0.1571 | 2.9207e+003 | 0.1014 |
| 9000 | 0.3618 | 0.1012 | 0.1002 |
| 10000 | 0.3379 | 0.0999 | 0.0999 |
5 结束语
本文对曲线拟合逆向云生成算法的初值进行优化选取,用数据的均值作为拟合初值进行曲线拟合,分析比较了3种生成算法的期望Ex、熵En和超熵He,得出曲线拟合算法逆向云生成算法比基本的逆向云生成算法的精度要高得多,而改进的曲线拟合算法对超熵的不稳定现象得到极大的改善,为云模型在定性评价以及数据挖掘等方面提供了更精确的理论依据。但是,逆向云生成的过程中不可避免地会有误差产生,关键在于构造一个相对准确的逆向云发生器,因此,在后续的研究中要利用更有效的方法生成更加精确的逆向云生成算法。
| [1] | 李德毅, 刘常昱. 论正态云模型的普适性[J]. 中国工程科学 , 2004, 6 (8) : 28-34 LI Deyi, LIU Changyu. Study on the universality of the normal cloud model[J]. Engineering Sciences , 2004, 6 (8) : 28-34 |
| [2] | 龙炜哲.基于云理论的遥感云图分类研究[D].南宁:广西大学, 2009: 18-35. LONG Weizhe. Remote sensing image cloud classification research based on cloud model theory[D]. Nanning: Guangxi University, 2009: 18-35. |
| [3] | 刘桂花, 宋承祥, 刘弘. 云发生器的软件实现[J]. 计算机应用研究 , 2007, 24 (1) : 46-48 LIU Guihua, SONG Chengxiang, LIU Hong. Software implementation of cloud generators[J]. Application of Computers , 2007, 24 (1) : 46-48 |
| [4] | 崔天宝.基于云模型的短期电价预测的研究[D].保定:华北电力大学, 2008: 10-18. CUI Tianbao. Short-term electricity price forecasting research based on cloud model[D]. Baoding: North China Electric Power University, 2008: 10-18. |
| [5] | 刘常昱, 冯芒, 戴晓军, 等. 基于云信息的逆向云新算法[J]. 系统仿真学报 , 2004 (11) : 2417-2420 LIU Changyu, FENG Mang, DAI Xiaojun, et al. A new algorithm of backword cloud[J]. Journal of Systerm Simulation , 2004 (11) : 2417-2420 |
| [6] | 张仕斌, 许春香. 基于云模型的信任评估方法研究[J]. 计算机学报 , 2013, 36 (2) ZHANG Shibin, XU Chunxiang. Study of trust evaluation approach based on cloud model[J]. Journal of Computer , 2013, 36 (2) |
| [7] | 李德毅, 孟海军, 史雪梅, 等. 隶属云和隶属云发生器[J]. 计算机研究和发展 , 1995 (13) : 16-21 LI Deyi, MENG Haijun, SHI Xuemei, et al. Membership cloud and membership cloud generator[J]. Journal of Computer Research and Development , 1995 (13) : 16-21 |
| [8] | 罗自强, 张光卫. 一种新的逆向云算法[J]. 计算机科学与技术 , 2007, 1 (2) : 234-240 LUO Ziqiang, ZHANG Guangwei. A new algorithm of backward cloud[J]. Journal of Frontiers of Computer Science and Technology , 2007, 1 (2) : 234-240 |
| [9] | 吕辉军, 王晔, 李德毅. 逆向云在定性评价中的应用[J]. 计算机学报 , 2003, 26 (8) : 1009-1014 LYU Huijun, WANG Ye, LI Deyi. The application of backward cloud in qualitative evaluation[J]. Journal of Computers , 2003, 26 (8) : 1009-1014 |
| [10] | 刘常昱, 李德毅, 杜鹢. 正态云模型的统计分析[J]. 信息与控制 , 2005, 34 (2) : 236-239 LIU Changyu, LI Deyi, DU Yi, et al. Some statistical analysis of the normal cloud model[J]. Information and Control , 2005, 34 (2) : 236-239 |
| [11] | 王辉, 于立君, 王科俊, 等. 一种可变模糊匹配阴性选择算法[J]. 智能系统学报 , 2011, 6 (2) : 178-184 WANG Hui, YU Lijun, WANG Kejun, et al. An adjustable fuzzy matching negative selection algorithm[J]. CAAI Transactions on Intelligent Systems , 2011, 6 (2) : 178-184 |
| [12] | 李众, 刘艳. 一维正态云模型单规则推理映射研究[J]. 系统仿真学报 , 2008, 20 (3) : 702-705 LI Zhong, LIU Yan. Research on one-dimension normal cloud model single rule reasoning[J]. Journal of System Simulation , 2008, 20 (3) : 702-705 |
| [13] | 王辉, 王科俊, 于立君. 基于模糊思想生成最有效检测器集的变阈值免疫算法[J]. 系统仿真学报 , 2008, 20 (17) : 4596-4600 WANG Hui, WANG Kejun, YU Lijun. Adjustable threshold immune algorithm of creating most effective detector set based on fuzzy idea[J]. Journal of System Simulation , 2008, 20 (17) : 4596-4600 |
| [14] | 刘衍民, 赵庆祯, 邵增珍. 基于正态云的粒子群优化算法及其应用[J]. 计算机工程与应用 , 2011, 37 (17) : 161-162 LIU Yanmin, ZHAO Qingzhen, SHAO Zengzhen. Particle swarm optimization algorithm based on normal cloud and its application[J]. Computer Engineering , 2011, 37 (17) : 161-162 |
| [15] | 李德毅, 杜鷁. 不确定性人工智能[M]. 北京: 国防工业出版社, 2005 : 271 -284. |



