2. 哈尔滨工程大学 自动化学院,黑龙江 哈尔滨 150001
2. College of Automation, Harbin Engineering University, Harbin 150001, China
图像分割是医学图像处理的重要内容之一,对医学图像中感兴趣的组织或器官进行精确地分割是对病变部位进行定性或定量分析的基础,也是对病变组织进行精确三维重建的重要前提。模糊聚类算法(fuzzy C-means,FCM)是一种非监督的聚类算法,已经被成功地应用到图像分割[1-6]中,但有两个缺点:1)由于FCM算法仅仅考虑了图像的灰度信息,没有对图像提供的空间邻域信息加以利用,使得医学图像分割无法取得令人满意的效果;2)FCM算法采用迭代的方式对定义的目标函数进行最小化,使得算法的运行效率低下。针对这些问题,许多研究者对传统的FCM算法进行了改进[7-13],如利用图像的统计信息提高算法效率,或者把像素的邻域信息考虑到图像的分割过程等,然而这些改进算法始终无法很好地平衡分割的效果与算法的运行效率。基于此,提出峰值检测的FCM算法,并将其应用于医学图像分割进行实验。
1 峰值检测的FCM算法 1.1 经典的FCM算法作为一种经典的聚类算法,FCM已经被广泛地运用到模式识别、目标检测等领域。FCM算法可以看作是对K-均值算法(K-means)的改进[13-14],其本质是用软处理代替传统的硬处理方式。在FCM算法中,目标函数定义为
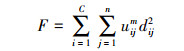 |
(1) |
式中:C是预先设置的聚类数目,n是图像中像素数目,m>1是模糊因子,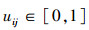

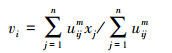 |
(2) |
应用FCM算法对图像进行分割就是最小化式中目标函数的过程,其目的是使所有的像素尽可能靠近相应的聚类中心,从而达到图像分割的目的。在FCM算法中,通常采用拉格朗日算子法最小化目标函数,即构造如下的函数:
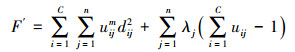 |
(3) |
通过
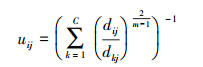 |
(4) |
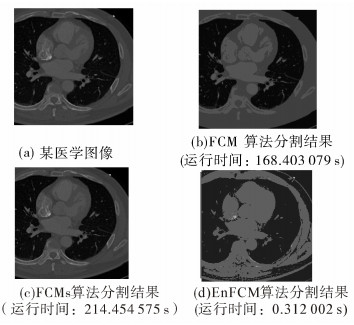
针对FCM算法的缺点,研究者相继提出了空间约束的FCM算法(FCMs)[7]和改进的FCM算法(EnFCM)[9]等相关算法。其中,FCMs算法对图像邻域信息的利用是在目标函数中加入邻域项,而EnFCM算法对算法效率的改进主要是借助图像的直方图进行。然而,在这些相关的改进算法中,始终无法很好地平衡分割的效果与算法的运行效率。以图 1中所示的医学图像分割结果为例加以说明。从图 1可以看出,FCM算法和FCMs算法的分割效果明显好于EnFCM算法,而EnFCM算法的运行效率又明显好于前两个算法。因此,如何有效地平衡算法的分割效果与运行效率,一直是FCM算法的研究热点,这也是本文的出发点。本文认为,FCM算法对图像中提供的信息远没有充分利用,以图 1(a)的直方图加以说明,如图 2所示。
|
| 图 1 几种算法对某医学图像的分割结果 Fig. 1 A medical image segmentation results of several algorithms |
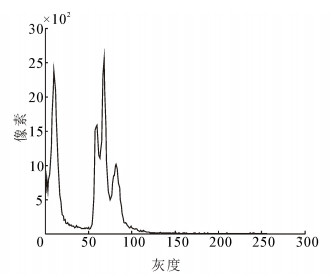
从图 2可以看出,该直方图具有4个明显的波峰,对应的灰度值分别是10、58、67和81,而运用FCM算法求得的最终聚类中心分别为10.223 7、57.590 0、68.671 2和86.451 6。可以发现,这4个峰值比较接近最终的聚类中心。如果初始化时能够使算法的聚类中心接近最终的聚类中心,则在迭代过程中必定可以有效减少算法的迭代次数,提高算法的运行效率。而在FCM、FCMs以及EnFCM等相关改进算法中,并没有考虑这一点,它们的初始聚类中心是在随机化产生隶属度的基础上计算的,通常情况下比较集中,因而导致了算法的运行效率低下。针对这个问题,提出了一种逼近策略,在获取到峰值的基础上计算相应的区间,利用区间信息初始化相应的聚类中心。算法的具体步骤如下:
|
| 图 2 图 1(a)的直方图 Fig. 2 Histogram of Fig.1(a) |
1)计算给定图像的直方图H;
2)计算直方图H上所有峰值的集合P,即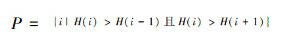
3)如果|P|≤C,转6),否则转4);
4)根据像素灰度值与峰值的距离,计算每个峰值i关联的像素数目,即
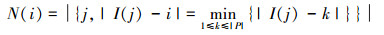 |
(5) |
5)删除关联像素数目最少的峰值,并将与其关联的像素与相邻的两个峰值重新关联,转3);
6)根据获取的峰值初始化聚类中心;
7)根据式(4)初始化像素的隶属度uij;
8)根据式(1)计算目标函数的值F;
9)根据式(2)计算聚类中心;
10)根据式(4)更新像素的隶属度;
11)根据式(1)计算目标函数的值F′;
12)如果F-F′<threshold,算法结束;否则,令F=F′,转9)。
1.3 聚类中心的初始化峰值检测的FCM算法的关键在于聚类中心的初始化,本部分将就这个问题进行讨论。初始化策略分为两步:
1)基于获取的C个峰值将直方图分割为C个区间,具体如下:
(1)第一个区间下界l1=0,上界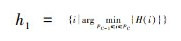
(2)最后一个区间上界hC=255,下界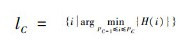
(3)其他区间下界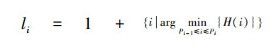

2)在所获取的C个区间上,初始化算法的聚类中心,如式(6):
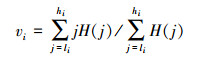 |
(6) |
与FCM及FCMs算法相比,本文算法有效地利用了图像的统计信息,因而可以有效地提高算法的运行效率;与EnFCM算法相比,算法在图像直方图的基础上进行了进一步的处理,本文算法利用峰值检测技术来指导聚类中心的计算,可以避免传统EnFCM算法中随机化产生隶属度的情况,保证最终的分割效果。
2 实验分析本部分将以图 3中的医学图像为例,将本文的算法与FCM、FCMs和EnFCM进行比较。需要说明的是,实验选取的医学图像是真实的医学图像,其尺寸为512×512。
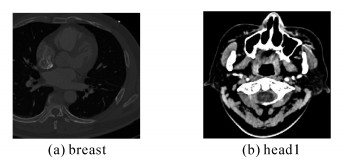
|
| 图 3 实验选取的医学图像 Fig. 3 Experimental images |
本部分对FCM、FCMs、EnFCM以及本文提出的峰值检测的初始化策略的分割结果进行视觉效果比较。实验过程中相关参数的设置如下:预设的聚类数目C=4,允许迭代的最大次数为100,m=1.75,α=2.0。同时,为了便于表示,将本文初始化聚类中心的策略表示为IntFCM。对图 3中4幅图像运用4种算法分割的结果如图 4所示。从图 4的breast分割结果中可以看出,FCM算法和FCMs算法由于在隶属度初始化时采取了随机产生的策略,因而无法很好地区分breast图像的主要成分,而EnFCM算法则对图像的细节部分无法很好地分辨,分割结果中小而碎的区域较多。而本文提出的峰值检测FCM算法则可以较好地分辨出图像的主要成份,这在图 2中的直方图中非常明显。换句话说,FCM和FCMs算法在最小化目标函数的过程中,将灰度值为58和67的峰值判定为同一类,而本文算法则可以有效地将二者分辨出来。同时,FCMs算法由于考虑了像素的邻域信息,因而分割后结果中的“琐碎区域”明显少于FCM算法的分割结果,分割的整体性较好。比较其余图像,得到本文的算法在上述4幅医学图像的分割结果较好,明显优于传统的模糊C均值算法(FCM)、基于空间约束的FCM算法(FCMs)和改进的FCM算法(EnFCM)的分割效果。
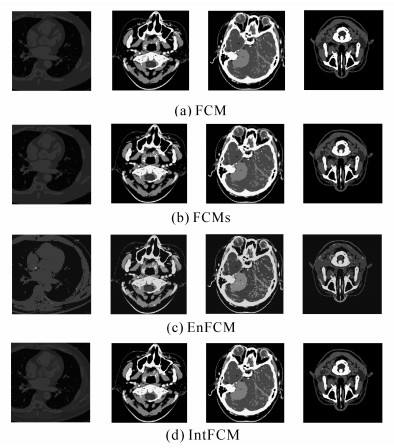
|
| 图 4 不同算法的分割结果 Fig. 4 The results of different image segmentation algorithms |
对于图像分割结果的质量比较,存在各种各样的标准,本部分将从聚类算法的角度出发,从中选择了4个标准,对涉及的4个算法进行比较。选择的相关标准如下所示。
1)第1个量化评价标准称为Bezdek划分系数[15],其定义如下:
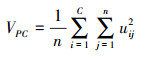 |
(7) |
从VPC的定义来看,一个好的聚类应使图像中像素属于某一类的隶属度尽可能大,而属于其他类的隶属度尽可能小。因此,一个好的聚类的VPC值应尽可能大。
2)本文选用的第2个量化标准是VXB,具体定义如下[16]:
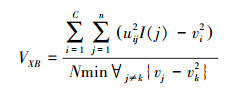 |
(8) |
从VXB的描述可以看出,VXB的值反映的是聚类内部的一种距离度量。由于在图像分割时希望聚类内部更紧致一些,因此,对一个好的聚类而言,其VXB值应稍小一些。
3)Liu在进行多分辨率彩色图像分割时,提出了一种Liu系数,用以描述分割后图像与原图像的差别[17],本文对其中的距离进行了修正,使其可以运用在灰度图像的分割效果评价上,定义如下:
 |
(9) |
式中:Ai是第i类中像素的数目,
从式(9)中F(I)的定义可以看出,一个好的聚类应该会使分割后图像与分割前图像的差距越小越好,即它对应着较小的F(I)值。
4)重构错误率(reconstruct error)是由Pedrycz提出的,指的是利用分割后的图像对原图像进行重构后,与原图像之间的差别[18-20],具体定义如下:
 |
(10) |
式中:I″(i)表示重构后图像中第i个像素的灰度值,定义如下:
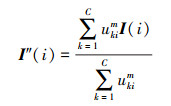 |
(11) |
从式(10)重构错误率的定义可以看出,对分割后的图像进行重构后,当然希望所得到的图像与原图像尽可能地相似,因此,一个好的图像分割算法应具有较小的重构错误率。
实验从上述4方面进行了比较,结果如表 1所示。从表 1可以看出,从Bezdek划分系数进行比较时,本文算法和FCM算法在这4种算法中表现较好,FCMs算法和EnFCM算法表现较差;从聚类内部的距离来看,本文算法要略好于FCM和FCMs算法,明显好于EnFCM算法,这说明本文算法的区域同质性更强;从Liu系数进行比较时,本文算法和FCM算法较好,FCMs算法由于考虑了邻域信息,所以其值比FCM稍大,EnFCM算法表现较差;在重构错误率方面,本文算法要略好于FCM和FCMs算法,明显好于EnFCM算法,这说明本文算法重构的图像更接近于原图像。
| 标准 | 算法 | breast | head1 | tumor | head2 |
| VPC | FCM | 0.908256 | 0.937925 | 0.920705 | 0.943104 |
| FCMs | 0.890121 | 0.910757 | 0.891943 | 0.923302 | |
| EnFCM | 0.780815 | 0.880399 | 0.856142 | 0.875697 | |
| IntFCM | 0.887940 | 0.937925 | 0.920705 | 0.943104 | |
| VXB | FCM | 1.708753 | 1.528459 | 3.980954 | 1.269151 |
| FCMs | 1.721053 | 1.529560 | 1.575088 | 6.249228 | |
| EnFCM | 1.705063 | 3.370459 | 1.704269 | 1.702875 | |
| IntFCM | 2.086202 | 1.528461 | 1.574369 | 1.269151 | |
| F(I) | FCM | 0.375072 | 1.785398 | 1.611865 | 1.164947 |
| FCMs | 0.383582 | 2.034325 | 1.77718 | 1.298093 | |
| EnFCM | 3.054808 | 4.162635 | 4.45105 | 4.353452 | |
| IntFCM | 0.373781 | 1.785398 | 1.611865 | 1.164947 | |
| VRE | FCM | 39.986882 | 96.725345 | 106.032120 | 61.193914 |
| FCMs | 40.237596 | 105.220373 | 114.231665 | 67.188700 | |
| EnFCM | 288.00562 | 630.001101 | 542.438503 | 686.889253 | |
| IntFCM | 37.937884 | 96.725322 | 106.032094 | 61.193855 |
从对聚类算法的4个衡量标准综合来看,本文提出的基于区间计算的聚类中心初始方案由于充分考虑了区间提供的信息,其结果可以与FCM算法相媲美,明显优于FCMs算法和EnFCM算法。
2.3 运行时间比较考虑到本文最初的出发点是在保证分割结果的前提下提高FCM算法的效率,因此,需要对算法的运行时间进行比较,结果如表 2所示。需要说明的是,4个算法均运行在相同的计算机软硬件环境,编程环境采用MATLAB 2010b。
| 算法 | breast | head1 | tumor | head2 |
| FCM | 197.921 875 | 163.937 5 | 212.390 625 | 177.875 000 |
| FCMs | 427.046 875 | 365.687 5 | 561.609 375 | 304.640 625 |
| EnFCM | 0.453 125 | 0.453 125 | 0.484 375 | 0.453 125 |
| IntFCM | 102.687 5 | 114.718 75 | 119.578 125 | 151.312 500 |
从表 2可以看出,虽然文中算法在运行效率上明显不如EnFCM算法,但较FCM算法和FCMs算法有明显地提高,满足了本文最初的要求。
3 结束语FCM算法用于医学图像分割时存在低效率问题,其相关改进算法在效率与分割效果方面又很难取得平衡,针对这个问题,本文提出了基于峰值检测的FCM算法,其本质是在FCM算法进行初始化时使初始化的聚类中心逼近最终的聚类中心,以提高算法的效率。在医学图像上的实验表明,本文算法在视觉效果、图像分割质量方面,要优于FCM及其相关改进算法;相比于FCM和FCMs算法,其运行效率有所提高,但与EnFCM算法仍有较大的差距。在接下来的工作里,将继续研究如何保证分割效果的前提下进一步提高算法的运行效率,使其与EnFCM在运行效率上可以相媲美。
| [1] | 徐少平, 刘小平, 李春泉, 等. 基于区域特征分析的快速FCM图像分割改进算法[J]. 模式识别与人工智能 , 2012, 25 (6) : 987-995 XU Shaoping, LIU Xiaoping, LI Chunquan, et al. An improved fast FCM image segmentation algorithm based on region feature analysis[J]. Pattem Recognition and Aitificial Intelligence , 2012, 25 (6) : 987-995 |
| [2] | HE Lianghua, WEN Ying, WAN Meng, et al. Multi-channel features based automated segmentation of diffusion tensor imaging using an improved FCM with spatial constraints[J]. Neurocomputing , 2014, 137 : 107-114 DOI:10.1016/j.neucom.2013.09.051 |
| [3] | 唐利明, 田学全, 黄大荣, 等. 结合FCMS与变分水平集的图像分割模型[J]. 自动化学报 , 2014, 40 (6) : 1233-1248 TANG Liming, TIAN Xuequan, HUANG Darong, et al. Image segmentation model combined with FCMS and variational level set[J]. Acta Automatica Sinica , 2014, 40 (6) : 1233-1248 |
| [4] | CAO H B, DENG H W, WANG Y P. Segmentation of M-FISH images for improved classification of chromosomes with an adaptive fuzzy C-means clustering algorithm[J]. IEEE Transactions on Fuzzy Systems , 2012, 20 (1) : 1-8 DOI:10.1109/TFUZZ.2011.2160025 |
| [5] | 张小峰.基于模糊聚类算法的医学图像分割技术研究[D].济南:山东大学, 2014: 7-20. ZHANG Xiaofeng. Research of medical image segmentation based on fuzzy clustering algorithm [D].Jinan: Shandong University, 2014: 7-20. |
| [6] | KANNAN S R, RAMATHILAGAM S, SATHYA A, et al. Effective fuzzy C-means based kernel function in segmenting medical images[J]. Computers in Biology and Medicine , 2010, 40 (6) : 572-579 DOI:10.1016/j.compbiomed.2010.04.001 |
| [7] | AHMED M N, YAMANY S M, MOHAMED N, et al. A modified fuzzy c-means algorithm for bias field estimation and segmentation of MRI data[J]. IEEE Trans Med Imaging , 2002, 21 (3) : 193-199 DOI:10.1109/42.996338 |
| [8] | CHUANG K S, TZENG H L, CHEN S, et al. Fuzzy C-means clustering with spatial information for image segmentation[J]. Computerized Medical Imaging and Graphics , 2006, 30 (1) : 9-15 DOI:10.1016/j.compmedimag.2005.10.001 |
| [9] | SZILAGYI L, BENYO Z, SZILAGYI S M, et al. MR brain image segmentation using an enhanced fuzzy c-means algorithm[C]. //Proceedings of 25th Annual International Conference of IEEE EMBS. Cancun, Mexico, 2003: 17-21. |
| [10] | 张保威, 钱慎一, 宋宝卫. 改进FCM在医学图像分割中的应用[J]. 计算机工程 , 2012, 38 (14) : 193-195 ZHANG Baowei, QIAN Shenyi, SONG Baowei. Application of improved FCM in medical image segmentation[J]. Computer Engineering , 2012, 38 (14) : 193-195 |
| [11] | 吴林, 郭大勇, 施克仁, 等. 改进的FCM在人脑MR图像分割中的应用[J]. 清华大学学报:自然科学版 , 2004, 44 (2) : 157-159 WU Lin, GUO Dayong, SHI Keren, et al. Modified fuzzy c-means algorithm for image segmentation in brain magnetic resonance images[J]. Journal Tsinghua University:Sci & Tech , 2004, 44 (2) : 157-159 |
| [12] | MILIND M, MUSHIRIF, AJOY K. A-IFS histon based multithresholding algorithm for color image segmentation[J]. IEEE Signal Processing Letters , 2009, 16 (3) : 168-171 DOI:10.1109/LSP.2008.2010820 |
| [13] | LI Yang, YU Fusheng. A new validity function for fuzzy clustering[C]//Proceedings of the 2009 International Conference on Computational Intelligence and Natural Computing. Park City, USA, 2009: 462-465. |
| [14] | ZHANG Daoqiang, CHEN Songcan. A novel kernelized fuzzy C-means algorithm with application in medical image segmentation[J]. Artificial Intelligence in Medicine , 2004, 32 (1) : 37-50 DOI:10.1016/j.artmed.2004.01.012 |
| [15] | BEZDEK J C. Cluster validity with fuzzy sets[J]. Cybernetics , 1974, 3 (3) : 58-73 |
| [16] | XIE X L, BENIi G. A validity measure for fuzzy clustering[J]. IEEE Trans Pattern Anal Mach Intell , 1991, 13 (8) : 841-847 DOI:10.1109/34.85677 |
| [17] | LIU J Q, YANG Y H. Multi-resolution color image segmentation[J]. IEEE Trans Pattern Anal Mach Intell , 1994, 16 (7) : 689-700 DOI:10.1109/34.297949 |
| [18] | WITOLD P. Knowledge-based clustering[M]. Wiley-Interscience, 2005 : 46 -66. |
| [19] | GRAVES D, PEDRYCZ W. Kernel-based fuzzy clustering and fuzzy clustering: a comparative experimental study[J]. Fuzzy Sets and Systems , 2010, 161 (4) : 522-543 DOI:10.1016/j.fss.2009.10.021 |
| [20] | 贾旭, 崔建江, 薛定宇, 等. 基于感兴趣区域函数优化的静脉图像分割算法[J]. 模式识别与人工智能 , 2012, 25 (3) : 475-480 JIA Xu, CUI Jianjiang, XUE Dingyu, et al. Vein image segmentation algorithm based on function optimization in regions of interest[J]. Pattem Recognition and Aitificial Intelligence , 2012, 25 (3) : 475-480 |


