2. 肇庆学院 计算机学院,广东 肇庆 526061
2. School of Computer Science, Zhaoqing University, Zhaoqing 526061, China
全向移动机器人运动灵活,凭借着不改变位姿就可以向任意方向移动的独特运动优势,已经被广泛应用于人类的生产、生活实践中[1]。由于四轮全向移动机器人是一个结构复杂、强耦合、非线性的机械系统,各个轮子驱动电机间存在耦合现象,对其中任一电机的控制都会引起其他3个电机状态的变化,因此对各个电机进行解耦控制是十分迫切和必要的[2],目前国内外关于四轮全向移动机器人的电机解耦控制方面的研究报告仍比较少见[3-5]。
四轮全向移动机器人电机控制系统是一个典型的MIMO系统,对于多变量系统的解耦问题,通常均采用参考模型控制的方法进行,而关于这类解耦方法的研究目前已经有很多[6]。文献[7]对具有4个操作轮的小车控制系统,通过测量反馈和动力学模型,提出一种基于状态反馈的参考模型解耦控制方法;文献[8]针对具有参数跳变的多变量系统, 提出一种基于分层递阶结构的多模型自适应前馈解耦控制器;R. Suzuki等把模型参考与内模原理结合, 构造了一种基于内模的参考模型解耦控制方法[9];文献[10]通过将滑模变结构理论与模型参考方法融合, 设计了一种滑模模型参考控制方法;文献[11]把神经网络理论与模型参考方法结合, 提出基于多标量模型的感应电机神经网络逆控制结构, 实现感应电机系统的自适应解耦线性化;文献[12]将模糊控制引入感应电动机解耦变结构系统可以有效地抑制抖振,从而提出了采用模糊控制的感应电动机模型参考解耦控制系统。这些方法都是通过设计参考模型对控制器的参数进行调整,控制和解耦功能均由同一个控制器实现,难以同时兼顾控制与解耦的性能,而且设计原理和方法都较复杂,因此在工程实践中,寻求简单易行的有效解耦方法是目前普遍关注的问题。文献[13]提出了一种基于控制量一致思想的参考模型解耦方法,通过设计合理的解耦控制器,实现了耦合关系已知的双通道耦合模型的动静态解耦。然而却没有考虑更加复杂的多通道耦合系统及耦合关系不确定或未知的情况。
为此,提出一种基于动力学解析的四轮驱动机器人电机解耦控制方法。首先,通过动力学解析获得各轮驱动电机输入输出量之间的耦合关系式,然后基于控制量一致思想,设计了四轮机器人电机控制系统的解耦控制器,实现了控制功能与解耦功能的分离,且控制器结构简单,便于实际应用。仿真结果表明,针对不同的输入情况,四路电机都能够很好地跟踪各自的控制目标,实现了控制系统的动静态解耦。
1 各电机输入输出量间的耦合关系 1.1 四轮全向移动机器人的动力学模型目前,在全向移动机器人轮系分布系统设计中,主要有三轮均衡分布及四轮均衡分布2种类型。由于本实验室所用比赛足球机器人的射门机构的增加,导致4个全向轮不是对称分布,而是如图 1所示[14],前两轮夹角为120°,后两轮为90°。
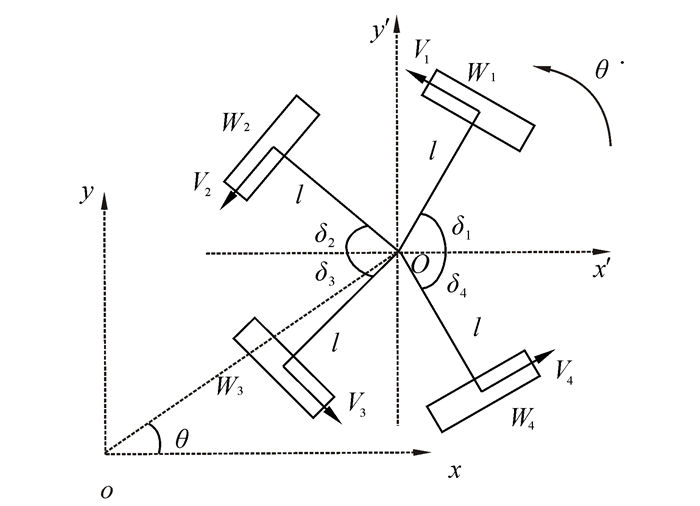
|
| 图 1 四轮全向机器人的结构 Fig. 1 Structure of the robot |
设机器人任一时刻质心的位姿为[x y θ)]T,φ1、φ2、φ3、φ4为4个车轮的角位移,取机器人广义位姿q=[x y θ φ1 φ2 φ3φ4]T,各轮转速为
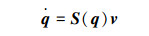 |
(1) |
式中:S(q)为转换矩阵,其表达式为
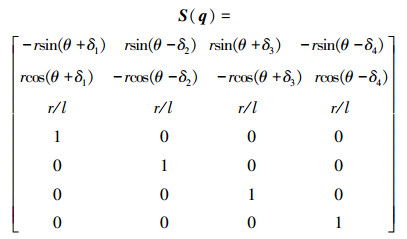 |
(2) |
式中,θ为机器人的运动方向,l为机器人质心到各轮子的距离,r为轮子的半径。
取机器人的质量为m,绕质心的转动惯量为J,机器人4个轮子受到的阻力分别为F1、F2、F3、F4,各个轮子的输出力矩为T1、T2、T3、T4,各个轮子的转动惯量分别为J1、J2、J3、J4,由牛顿第二定律可得动力学方程如下:
 |
(3) |
进一步整理为拉格朗日标准形式有
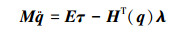 |
(4) |
式中:
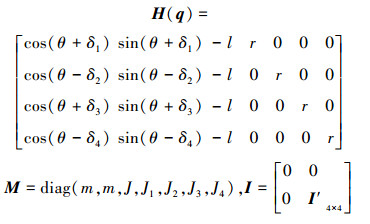 |
I'为单位对角方阵,
式(4)两端乘以ST(q),且由式(1)、(3)可得图 1所示的移动机器人动力学模型:
 |
(5) |
对式(1)两端求导,并将式(5)代入可得
 |
(6) |
取4×4的方阵Z和M分别为
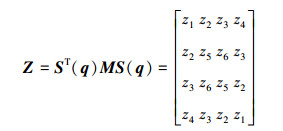 |
(7) |
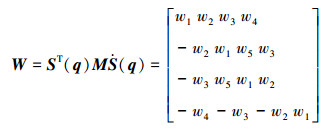 |
(8) |
其中矩阵Z中各元素的表达式为
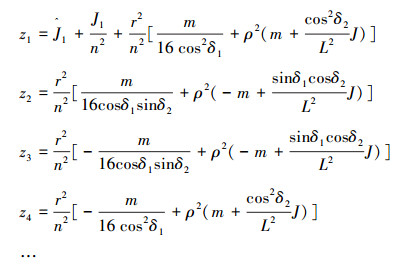 |
矩阵W中各元素的表达式为
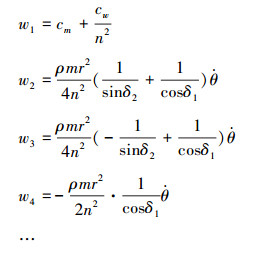 |
限于篇幅,其他系数未列出,其中Ĵi(i=1, 2, 3, 4)为折算到各个驱动电机的转动惯量,cm和cw分别为各个驱动电机和对应轮子的阻尼系数,n为电机齿轮减速比,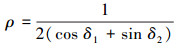
令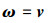
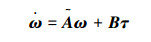 |
(9) |
式中:状态矩阵Ã和B为4×4的方阵,且
 |
(10) |
由式(8)和(10)可知,系统状态矩阵Ã是关于各轮转速的非线性矩阵,因此本文在实际计算中,用其在平衡点附近的近似线性化矩阵A来代替,从而有
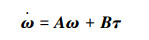 |
(11) |
由式(11)可知,四轮驱动机器人的电机控制系统是一个4输入4输出的耦合系统,需要进行解耦以达到对4个电机的独立控制。假设系统的输出方程为
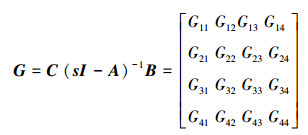 |
(12) |
通过式(12)就可求得各个电机输入量和输出量之间的耦合关系。
2 控制量一致解耦控制器设计 2.1 控制量一致解耦控制系统设计控制量一致解耦控制器设计如图 2所示。
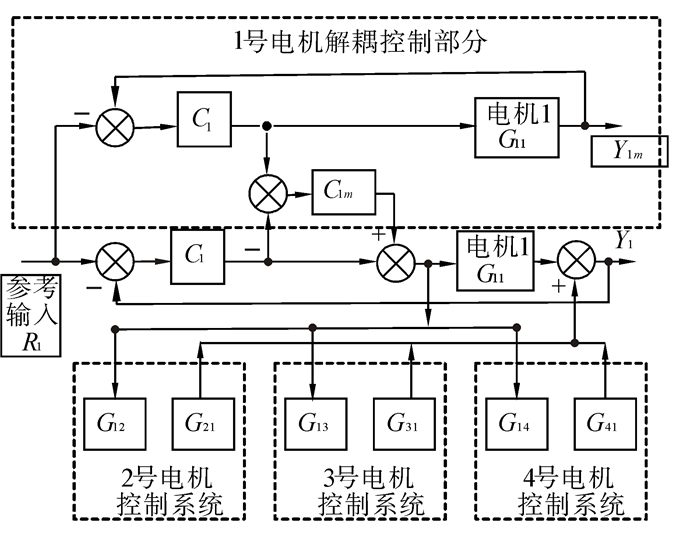
|
| 图 2 控制量一致解耦控制系统结构 Fig. 2 Structure of control system based on consistency controller outputs decoupling |
图 2中, 1号电机控制系统虚线内部分即为其解耦控制部分。主回路控制器C1, 是在不考虑耦合作用的条件下, 由要求的控制性能指标根据被控对象设计得到。在主回路控制器C1设计好后, 以系统实际输出Y1逼近参考模型输出Y1m为目的, 设计解耦控制器C1m,实现解耦控制。而由于基于控制量一致的原理进行解耦设计,使得解耦控制器只需调节一个增益系数就能实现系统解耦功能,因此大大简化了解耦控制器的设计。
从图 2中可知, 解耦回路与相应的主回路的控制器参数及传递函数完全相同, 这样当解耦控制实现解耦时,就不再需要调节主控制器的参数, 从而实现了控制和解耦功能的分离。
2.2 理论分析取1号电机在无耦合,单独独立控制时的输出为Y1m,G12、G13、G14分别为1号电机对其他3个电机的耦合作用,G21、G31、G41分别为其他3个电机对1号电机的耦合作用,这些量可由式(12)计算得到。取各个电机的传递函数分别为G11、G22、G33和G44,由图 2分析,列出系统的输出方程组得
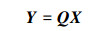 |
(13) |
式中:
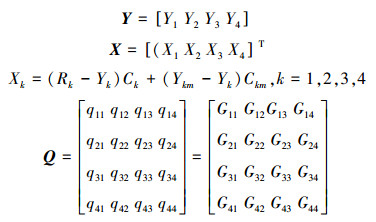 |
令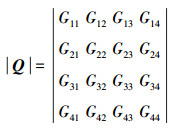
则对1号电机回路有
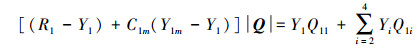 |
(14) |
整理得
 |
(15) |
又有
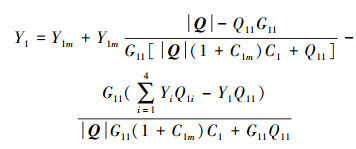 |
(16) |
由式(16)可知,如果传递函数矩阵行列式
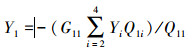
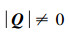
由于系统的控制器C1已经提前设计好,因此解耦控制器C1m只需要设计为一个大的增益比例系数就能满足系统控制要求,从而大大简化了解耦控制的设计,易于应用和实现。当系统完全解耦时,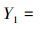
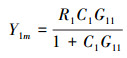
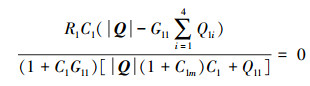 |
(17) |
因为C1、G11、Q、R1等均已知或者已经设计好,因此可以依据式(17), 按照解耦性能指标, 采用时域或者频域法,进行设计解耦控制器C1m。
3 仿真实验及分析为验证本文提出的控制方法的有效性,对机器人各个电机的速度响应进行仿真实验。所用到的机器人的具体参数与文献[14]相同,则由式(9)和(10)计算得到式(11)中2个状态矩阵及输出矩阵分别为
 |
仿真实验中C1为PID控制器,其3个参数分别取为10、0.01、0.5;解耦控制器C1m为一个比例增益系数,其值取为60。仿真实验分以下4种情况进行,仿真时间为5 s,因为4个电机情况相似,文中只给出1号电机和2号电机的响应曲线。图中,Y1m、Y2m分别表示没有耦合作用下1号电机和2号电机的理想输出,Y1c、Y2c分别表示未解耦时2个电机的输出响应曲线,Y1d、Y2d分别表示解耦以后两个电机的输出响应曲线。
情况1 1号电机的参考输入为单位阶跃信号,其他电机无输入信号时,所得的响应曲线如图 3。

|
| 图 3 情况1时的响应曲线 Fig. 3 Response curves of case 1 |
由图 3可以看出,未进行解耦控制时,由于其他电机耦合作用的影响,使得2号电机的输出不为0,而是一个幅值小于1 m/s的响应值,同时由于其他电机对1号电机的耦合作用,导致1号电机的输出响应的幅值也小于1 m/s,且存在一定的超调;当对各个电机的控制回路进行解耦以后,其他电机对2号电机的耦合作用被大大减小,2号电机的输出基本为0,同样其他电机对1号的耦合作用也被大大减小,1号电机能够很好地跟踪给定的阶跃输入。从而说明情况1时,本文方法能够很好地实现各个电机的解耦控制。
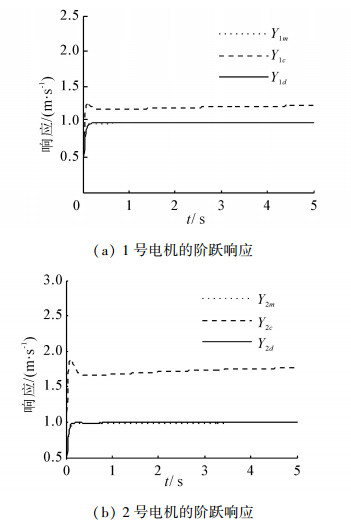
情况2 4个电机的输入信号均为单位阶跃信号时,所得的响应曲线如图 4所示,从图 4可以看出,未进行解耦控制时,由于其他电机对2号电机耦合作用的影响,使得2号电机的输出幅值大于1 m/s,同时由于耦合作用,导致1号电机的输出响应也不为1 m/s;进行解耦以后,各个电机间的相互耦合作用被大大削弱,各个电机均能很好地跟踪给定的阶跃输入,但是存在一定的静态误差。因此情况2时,本文方法能够很好地完成对整个电机控制系统的解耦控制。
|
| 图 4 情况2时的响应曲线 Fig. 4 Response curves of case 2 |
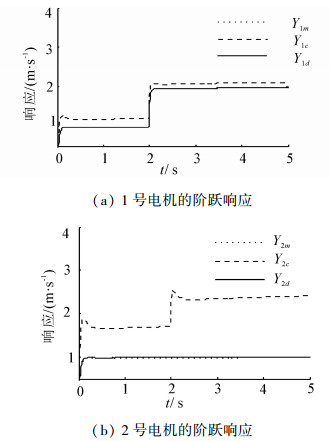
情况3 情况2中1号电机阶跃输入信号幅值在2s时由1 m/s突变为2 m/s,响应曲线如图 5。
|
| 图 5 情况3时的响应曲线 Fig. 5 Response curves of case 3 |
由图 5可以看出,未进行解耦控制时,在t=2s1号电机的输入发生了变化,从而导致2号电机的输出也在该时刻产生了跳变,由于耦合作用的影响,使得各个电机均不能跟踪指定的输入;进行解耦以后,1号电机和2号电机均能很好地跟踪既定输入,同时1号电机在t=2s的响应非常平稳,整个响应过程具有良好的动态性能。从而说明情况3时,当输入信号存在一定的变化时,本文方法也能够很好地实现各个电机的解耦控制。
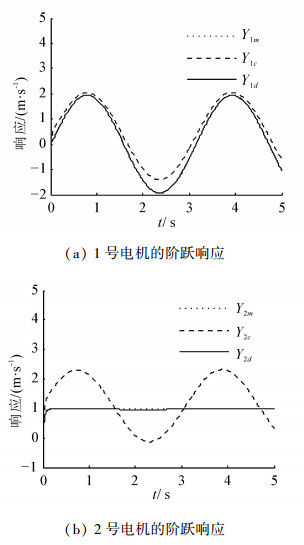
情况4 1号电机的输入为正弦信号R1=2sin(4πt),其他电机为单位阶跃信号时,所得的响应曲线如图 6所示。
|
| 图 6 情况4时的响应曲线 Fig. 6 Response curves of case 4 |
由图 6可以看出,未进行解耦控制时,1号电机的输入由于时刻在变化,从而导致2号电机的输出不是恒值而是正弦曲线,同时由于耦合作用的影响,1号电机也不能很好地跟踪指定的输入,存在很大的偏差;进行解耦以后,1号电机和2号电机均能很好地跟踪各自的既定输入,同时整个响应过程具有良好的动态性能。从而说明情况4时,即使输入信号在时刻变化,本文方法依然能够很好地实现各个电机的解耦控制。
同时为了进一步说明解耦的性能,定义
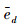
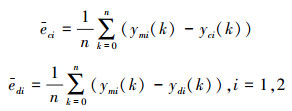 |
(18) |
式中:n为总的采样数,i为电机的编号。
表 1为4种不同情况下的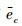
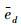
| 仿真情况 | 电机1ec/ed | 电机2ec/ed |
| 情况1 | 0.106 2/0.001 3 | 0.612 9/0.005 5 |
| 情况2 | 0.214 6/0.001 9 | 0.711 8/0.006 4 |
| 情况3 | 0.161 3/0.001 3 | 1.061 5/0.010 3 |
| 情况4 | 0.272 9/0.002 4 | 0.328 4/0.003 0 |
由图 3~6以及表 1可知,在各电机控制系统相互耦合的情况下,解耦控制器可以保证各个电机在一定的误差范围内,完成对期望输入的跟踪,解耦以后的误差约为解耦前的10-2,从而跟踪精度大大增加。但是这个静态误差却不能消除,这是因为受系统稳定性和实际条件的限制,解耦控制器的增益不能达到无限大值。尽管如此,解耦控制器仍能有效减小耦合因素的影响,基本实现了系统的动态和静态解耦。
由以上分析可知,若要达到满意的解耦效果,需要保证控制器(1+C1m)C1的动态和静态增益远大于被控对象G11,因此为了进一步降低静态误差,可在满足系统稳定性的前提下,适当提高原回路控制C1的动态和静态增益;同时对于C1m的设计,可通过引入积分环节修正为PI或者PID控制,而不是本文采用的较大比例系数的P控制。
4 结束语针对四轮全向移动机器人电机控制系统中存在的强耦合问题,通过动力学解析方法推导获得各个电机输入量和输出量之间的耦合关系,在此基础上,采用控制量一致思想设计了解耦控制器,实现了控制器的控制功能和解耦功能的有效分离,解决了传统参考模型解耦方法中控制器不能同时兼顾控制性能和解耦性能的问题,在一定误差允许范围内,实现了系统的动态和静态解耦。同时该控制器只需调整一个增益系数即可完成控制系统的解耦,结构简单,易于设计,便于实现和应用。
| [1] | JEFRI E M S, MOHAMED R, SAZALI Y. Designing omni-directional mobile robot with mecanum wheel[J]. American Journal of Applied Sciences , 2006, 3 (5) : 1831-1835 DOI:10.3844/ajassp.2006.1831.1835 |
| [2] | KIM C H, KIM B K. Minimum-energy translational trajectory generation for differential-driven wheeled mobile robots[J]. Intelligent and Robotic Systems , 2007, 49 (4) : 367-383 DOI:10.1007/s10846-007-9142-0 |
| [3] | 熊蓉, 张翮, 褚健, 等. 四轮全方位移动机器人的建模和最优控制[J]. 控制理论与应用 , 2006, 23 (1) : 96-98 XIONG Rong, ZHANG He, CHU Jian, et al. Modeling and optimal control of omni-derectional mobile robots[J]. Control Theory & Applications , 2006, 23 (1) : 96-98 |
| [4] | 刘开周, 董再励, 孙茂相. 一类全方位移动机器人的不确定扰动数学模型[J]. 机器人 , 2003, 25 (5) : 399-403 LIU Kaizhou, DONG Zaili, SUN Maoxiang. Mathematical model with uncertainty for a class of omni-direction mobile robot[J]. Robot , 2003, 25 (5) : 399-403 |
| [5] | 宋海涛, 张国良, 王仕成, 等. 全向移动机器人最短时间控制[J]. 电机与控制学报 , 2008, 12 (3) : 337-342 SONG Haitao, ZHANG Guoliang, WANG Shicheng, et al. Minimum time control for omni-directional mobile robot[J]. Electric Machines and Control , 2008, 12 (3) : 337-342 |
| [6] | 刘成, 赵福宇, 侯素霞, 等. 一种新的多变量参考模型解耦控制的方法[J]. 控制工程 , 2009, 16 (1) : 12-15 LIU Cheng, ZHAO Fuyu, HOU Suxia, et al. A reference model decoupling method for multivariable systems[J]. Control Engineering of China , 2009, 16 (1) : 12-15 |
| [7] | MARINO R, CINILI F. Input-output decoupling control by measurement feedback in four-wheel-active-steering vehicles[C]//Proceedings of the 45th IEEE Conference on Decision and Control. San Diego, USA, 2006: 1715-1720. |
| [8] | 王昕, 李少远. 多模型分层递阶自适应前馈解耦控制器[J]. 控制与决策 , 2005, 20 (1) : 17-22 WANG Xin, LI Shaoyuan. Hierarchical multiple model adaptive feedforward decoupling controller[J]. Control and Decision , 2005, 20 (1) : 17-22 |
| [9] | SUZUKI R, TORITA T, KOBAYASHI N, et al. Internal model control scheme for sensorless force control and its application to rubbing machines[C]//Proceedings of the IEEE Conference on Industrial Electronic and Applications, Singapore, 2006: 1-6. |
| [10] | EL-SOUSY F F M. An intelligent model-following sliding-mode position controller for PMSM servo drives[C]//Proceedings of the 4th IEEE International Conference on Mechatronics. Kumamoto, Japan, 2007: 1-6. |
| [11] | 王新. 基于多标量模型的感应电机神经网络逆控制[J]. 电气传动 , 2010, 40 (12) : 43-47 WANG Xin. Neural network inverse control of induction motor based on multiscalar model[J]. Electric Drive , 2010, 40 (12) : 43-47 |
| [12] | 邱焕耀, 毛宗源. 采用模糊控制的感应电动机解耦变结构控制系统的研究[J]. 自动化学报 , 1998, 24 (3) : 391-394 QIU Huanyao, MAO Zongyuan. The study of decoupling-variable structure system with fuzzy control[J]. Acta Automatica Sinica , 1998, 24 (3) : 391-394 |
| [13] | 刘成, 赵福宇, 侯素霞, 等. 一种基于控制量一致的参考模型解耦方法[J]. 控制工程 , 2009, 16 (5) : 571-574 LIU Cheng, ZHAO Fuyu, HOU Suxia, et al. A reference model decoupling method based on consistency controller outputs[J]. Control Engineering of China , 2009, 16 (5) : 571-574 |
| [14] | CHEN J P, WANG J B, YANG Y M. A motion control method of four-wheel drive omni-directional mobile robots based on multi points preview control[J]. Journal of Theoretical and Applied Information Technology , 2012, 45 (1) : 278-284 |


