理论与实践是密切相关的,计算理论为实际工作者提供了在计算机工程中使用的理性工具[1]。计算复杂性是计算理论的重要分支,它告诉人们问题求解需要多少资源(时间或空间)。它所涉及到的一些典型的难解问题包括旅行商问题[2]、SAT问题(可满足性问题,它涉及芯片测试、计算机设计、软件工程等应用领域[2])、电路复杂性问题[3]、博弈问题[1]等。通过对计算复杂性的研究,可以更深入地了解计算机的能力及局限性。研究问题的复杂性可以了解该问题求解的难易程度,如果它被证明是难解的,就不必将大量精力花费在寻找有效的求解算法上[1],从而在实际工作中做出理性的抉择。本文介绍了与计算复杂性相关的基本概念,同时综述了目前的研究状况,通过例子分析了各个计算复杂性类的特点及其证明的方法。并对各个计算复杂性类之间的关系作了详细的分析。
1 计算复杂性计算复杂性是计算理论的一个分支,它用于衡量问题被求解所需资源(比如时间或空间)的多少[1],在介绍时间复杂性和空间复杂性之前,先来了解计算理论中的一些基本概念。
1.1 可判定问题可判定问题是指该问题在算法上是可解的,即该问题在计算模型(如有穷自动机或图灵机)上执行,能够进入接受或拒绝状态而终止计算(即停机状态[4])。不可判定问题是指该问题在算法上是不可解的,即该问题在计算模型上执行不能进入停机状态,即不停机[4]。
1.2 确定型图灵机及非确定型图灵机 1.2.1 确定型图灵机图灵机(deterministic Turing machine, DTM)(见图 1)是一种通用的计算模型[5],该模型由图灵(Alan Turing)在1936年提出[1],能模拟实际计算机的所有计算行为。它用一个无限长的带子作为它的无限存储,有一个读写头,能在带子上读、写符号和左右移动。初始时,带子上只有输入串,其他地方都是空的,如果需要保存信息,它可能将这个信息写在带子上,为了读已经写下的信息,它可将读写头往回移动到这个信息所在的位置。机器持续地计算,直到产生输出为止。机器预置了接受和拒绝2种状态,如果进入这2种状态,就产生输出接受或拒绝。如果不能进入任何接受或拒绝状态,就继续执行下去,永不停止。
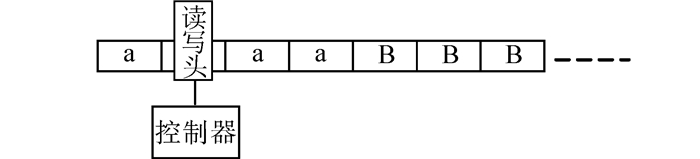
|
| 图 1 图灵机示意 Fig. 1 The diagram of Turing machine |
由于它具有无限的存储带,带上可读也可写,读写头可在带上左右移动等特点,所以相对于另外2种计算模型——有穷自动机[1](它的存储资源是有限的)和下推自动机[1](其栈内信息“先进后出”),它具有更强的描述求解某问题的算法的能力。例如:确定型图灵机可以判定语言A(即,所有由0组成、长度为2的方幂的字符串),A={02n|n≥0}。该语言(语言是对问题的形式化描述[5])的算法描述[1]DTM M2如下:
对于输入字符串w:
1)从左往右扫描整个带子,隔一个字符消去一个0;
2)如果在第1)步之后,带子上只剩下唯一的一个0,则接受;
3)如果在第1)步之后,带子上包含不止一个0,并且0的个数是奇数,则拒绝;
4)读写头返回至带子的最左端;
5)转到第1)步。
第1)步每重复一次,就会消去带子上一半的0。如果执行一次第1)步后,带子上的0的个数是大于1的奇数,说明带子上原有的0的个数不可能是2的方幂,因此拒绝[1]。显然该算法M2判定该语言。对于存储资源有限的有穷自动机是无法描述该算法的,而对于下推自动机,虽然具有无限存储的栈,但由于栈的“先进后出”的特点,无法实现隔一个字符消去一个0,由此可见图灵机具有更强的描述问题的能力。
1.2.2 非确定型图灵机确定型图灵机在计算过程中,下一步动作只有一种可能;而非确定型图灵机[5](nondeterministic Turing machine, NTM)是指在计算过程中,机器可以在多种可能性动作中选择一种继续进行,其计算是一棵树,不同分支对应机器不同的可能性[5]。如果计算的某个分支导致接受状态,则机器接受该输入。
非确定型图灵机并不对应任何实际的计算设备,它是一种假想的机器[7]。但它是一个有用的数学定义,有些问题更适于采用非确定型图灵机来描述,如计算机博弈问题,某走棋方在走棋时有多种走法可选择,这与非确定型图灵机的计算过程相同。
每个非确定型图灵机都等价于一个确定型图灵机[1]。也就是说这2种图灵机在能力上是等价的。文献[7]中给出如下定理:如果一个确定型图灵机去模拟一个t(n)时间的非确定型图灵机,则所需时间为2O(t(n))。
1.3 映射可归约性概念 问题A是映射可归约到问题B的,如果存在可计算函数f,使得对每个w,w∈A⇔f(w)∈B,记做A≤mB。称f为A到B的归约[1]。
作用 它旨在将一个问题转化为另一个问题,且使得可以用第2个问题的解来解第1个问题。如果问题A可归约到问题B,就可用B的解来解决问题A[3]。例如:在一个城市认路,可以借助于城市地图,这样就将城市认路问题归约到城市地图问题。
2 时间复杂性时间复杂性是指求解一个问题所需多少时间。对于固定规模的问题,其所需时间是一个常量;对于任意规模的问题,一般采用渐近记法[1],衡量其求解的复杂程度。如:函数f(n)=n3+n2+1,利用渐近记法,则该函数的时间复杂性为O(n3)(其中O表示一个常数),因为最高次项的影响占主导地位。另外,也可以通过证明,给一些问题的时间复杂性分类来说明该问题求解的难易程度。
2.1 确定型多项式时间复杂性确定型多项式时间复杂性(deterministic polynomial time,P)是指可以在确定型图灵机上以多项式时间解决的问题的集合[6]。一般认为多项式时间算法已经足够快了,而指数时间的算法很少采用[1]。属于P复杂性类的问题,被认为是容易求解的[8]。属于P类的例子:2个数是否是互素的问题,即RELPRIME={〈a, b〉| a与b互素}[1];如果1是同时整除2个数的最大整数,则称这2个数是互素的。如9和10就是互素的。一种快速地判断2个数是否互素的方法是采用欧几里德算法(Euclidean algorithm)[9]来计算2个自然数a和b的最大公因子,记为gcd(x, y)[10],它是能够整除2个自然数的最大整数,如:gcd(12, 15)=3。显然若gcd(x, y)=1,说明x和y是互素的。欧几里德算法用伪代码描述[9]如下:
function gcd(a, b)
while b≠0
t←b(“←”表示赋值)
b←a mod b(“mod”表示求余运算)
a←t
return a
该算法输出的值就是a和b的最大公因子。
算法R以gcd(a, b)为子程序求解RELPRIME[1]。
R=“对输入〈a, b〉,a和b是自然数:
1)运行子程序gcd(a, b)。
2)若结果为1,就接受;否则,就拒绝。”
算法R的复杂性分析:显然,算法R的复杂性由欧几里德算法的复杂性决定。欧几里德算法的复杂性问题已经被彻底研究过了,其复杂性为h2(h为2个自然数中最小的那个数的位数)[11],因此算法R的复杂性是h2,属于P类,即多项式时间算法。
2.2 非确定型多项式时间复杂性非确定型多项式时间复杂性(nondeterministic polynomial time,NP)是指可以在非确定型图灵机上以多项式时间解决的问题的集合[6]。而前面在图灵机的阐述中提到过,一个确定型图灵机去模拟一个t(n)时间的非确定型图灵机,所需时间为2O(t(n)),所以属于P类的问题与属于NP类的问题在求解的时间上存在指数级的差异。可见NP类的问题被怀疑是难解的[8]。到目前为止,还不清楚NP类问题是否存在有效的多项式时间算法[8]。但是去验证某个问题是否成立是可以在多项式时间完成的[1],比如:合数问题(当一个自然数是2个大于1的整数的乘积,称该自然数为合数),虽然还没有找到一个有效的多项式时间算法,但可以比较容易地去验证一个数是否是合数,这只需找到该数的一个因子[1],比如24,它可以是4和6的乘积,因此它是合数。所以NP是具有多项式时间验证机(验证算法)的问题的集合[1]。
NP类问题的举例 判定一个无向图是否包含指定大小的团的问题属于NP [12],令CLIQUE={〈G, k〉| G是包含k团的无向图}。
团的概念 如果C是无向图的顶点集V的子集,而且任意2个C中的顶点都有边连接,则称顶点集C为该无向图的团[2]。文献[1]给出一种判定团的非确定型多项式时间算法,如下:
N=“对输入〈G, k〉,其中G是一个无向图:
1)非确定性地选择G中k个结点的子集;
2)检查G是否包含链接C中结点的所有边;
3)若是,则接受;否则,拒绝。”
算法分析 该算法是运行在非确定型图灵机上,当然,现实中并没有这种设备,这是一种假想,假设存在这种机器,该算法在非确定型图灵机上以多项式时间运行,而确定型图灵机才是现实中计算机的雏形,所以该算法在计算机上将以指数时间运行,也就是说该算法是不可取的,说明团问题是难解的。
2.3 NP的完全问题(NP-complete)一个语言B属于NP-complete,如果它满足2个条件:
1)B属于NP;
2)每个属于NP的问题在多项式时间内可以归约到B[1]。
NP-complete问题被认为是NP类中最难的[2],Cook[12]找到并证明了第一个属于NP-complete的问题[13],即SAT[12](satisfiability, 可满足性问题[14]),可以根据映射可归约性, 证明某个问题属于NP-complete。如果某个问题被证明属于NP-complete,则说明该问题不存在有效的多项式时间算法,因此就可以不用将精力花费在寻找有效算法上了[1]。对于NP-complete的定义,如果B仅仅满足条件2,这说明该问题本身并不属于NP,可以说它是NP-hard[1]。因而该问题可能更加难解。
NP-complete例子顶点覆盖问题[15]。
无向图G的顶点覆盖是一个顶点集合V,使得G中的每一条边都接触V中的至少一个顶点[16]。顶点覆盖问题旨在确定图中是否存在指定规模的顶点覆盖:
VERTEX-COVER={〈G, k〉|G是具有k个结点的顶点覆盖的无向图}[1],顶点覆盖问题属于NP-complete类问题[12]。
对于证明某个问题A属于NP-complete,需要依据NP-complete的定义,具体步骤如下:
1)证明A属于NP;
2)需要找到一个已被证明是NP-complete的问题B;
3)证明B可归约到A;
4)证明该归约可在多项式时间内完成。
这里步骤3)是难点,需要一些别出心裁的巧妙思维去构造一个合理的归约函数,文献[1]中,使用已经被证明属于NP-complete的问题3SAT(3SAT,是一个合取范式,该公式中每一个子句都有3个文字,它是Karp[12]的21个NP-complete问题的其中之一),设该3SAT公式为(x∨x∨y)∧(x∨y∨y)∧(x∨y∨y),并且构造了一个归约,如图 2。
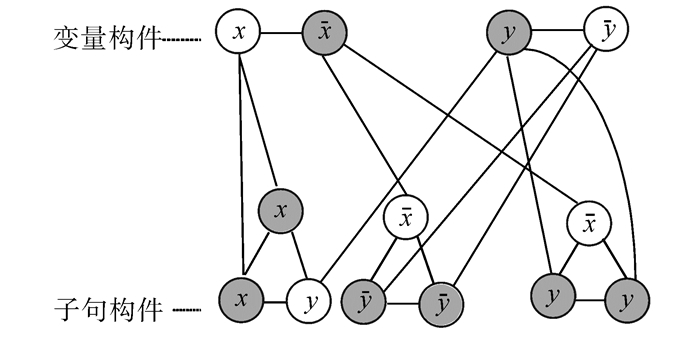
|
| 图 2 归约的完整结构图 Fig. 2 The complete structure of reducibility |
图中包括变量构件和子句构件,变量构件关系对变量的赋值;子句构件对应公式中的3个子句。图中共有2m+3l(m表示公式中变量的数量,l表示公式中子句的数量)个顶点,令指定的顶点覆盖规模k=m+l,根据此3SAT公式,k的值为8,因此要从图中找到满足该3SAT公式的规模为8的顶点覆盖。
规则[1] 首先为2个变量选取满足公式的赋值,即x为假、y为真,选择变量构件中相应的结点作为顶点覆盖中的结点,然后在各个子句构件中选择值不为真的2个结点作为顶点覆盖中的结点,其中第3个子句的3个变量的值都为真,则将不影响顶点覆盖的结点x去除,选择该子句中的另外2个结点,如图中有阴影的结点,这些结点的集合构成该图的一个顶点覆盖。因此说明该图中的顶点覆盖,可以满足该3SAT公式(即该公式的值为真),进而说明3SAT可归约到顶点覆盖,也就是说3SAT问题可以在顶点覆盖问题上求解,根据NP-complete定义可知,顶点覆盖问题属于NP-complete。
2.4 指数时间复杂性(exponential time,EXPTIME)该复杂性类是一些确定型问题的集合,这些问题可以使用确定型图灵机在O(2p(n))的时间内解决,这里的p(n)代表的是n的某个多项式。属于该复杂性的问题,它的难度不小于P、NP、NP-complete以及空间复杂性类(PSPACE和PSPACE-complete)[3]。
EXPTIME例子 G3[17]游戏,该游戏中的每个局面(position)是一个四元组(τ, W-LOSE(X, Y), B-LOSE(X, Y), α′),其中τ∈{W, B},它表示当前走棋方,W-LOSE=C11∨C12∨C13∨…∨C1p和B-LOSE=C21∨C22∨C23∨…∨C2q是属于12DNF[18]的布尔公式,其中每个C1i(1≤i≤p)和C2j(1≤j≤q)是最多12个文字之间的与运算,每个文字是集合X(Y)中的一个变量,如:z或z(变量z的非运算);α′是对公式X∪Y的一个赋值,如:X={x1, x2, x3},Y={y1, y2, y3},则X∪Y={x1, x2, x3, y1, y2, y3},对X∪Y赋值,就是对该集合中的各个元素赋值为0或1。
比赛双方交替进行,W方或B方通过改变集合X和Y中的一个变量的值进行走棋。更精确地,W方能够从局面(W, W-LOSE(X, Y, B-LOSE(X, Y), α′)下棋到局面(B, W-LOSE(X, Y), B-LOSE(X, Y), α′),当且仅当α′与α′’不同,并且在α′的赋值下,W-LOSE(X, Y)的布尔值为false。如果在W(B)走了若干步后,公式W-LOSE(B-LOSE)为true,那么W(B)失败。
在文献[17]中,给出了四元组中的公式F(即W-LOSE(X, Y)或B-LOSE(X, Y))的所有可能的表示形式共有:card(V(F))≤e×|F|/log(|F|),其中,e为常量,|F|表示公式F被编码后的长度,V(F)表示公式F所有可能的表示形式所构成的集合,card(V(F))表示集合中的元素总数。而对于表示G3游戏局面的四元组,对于player I(player II),通过对集合X(Y)中的一个变量的赋值来完成下棋,而该变量的值有2个,即0或1。所以,某个走棋方在下棋时,可走的局面有2个,即对于一个F的表示形式,由于四元组有2种可能,所以,从第一步开始一直到分出胜负,共有e×|F|/log(|F|)个2相乘,即2e×|F|/log(|F|)。又用τ来识别走棋方,即第一步谁先走有2种可能,并且该四元组中有2个公式F(即W-LOSE(X, Y)和B-LOSE(X, Y)),因此,对一个输入w,其中n表示w的长度,则G3从开始走棋到分出胜负,共产生的局面的数量为2×22en/log(n),用渐近记法表示,为2O(n/log(n)),是指数级的。即该游戏属于EXPTIME问题。
3 空间复杂性空间复杂性是指求解一个问题所需多少空间。属于某空间复杂性类的问题,它的求解难度要大于属于时间复杂性类的问题,因为运行快的算法不可能消耗大量的空间,也就是说在每个计算步上最多能访问一个新单元,所以,任何在时间t(n)内运行的机器最多能消耗t(n)的空间[1]。与时间复杂性一样,也是采用渐近记法来计算求解问题的空间复杂性。另外,也可以通过证明,给一些问题的空间复杂性分类来说明该问题求解的困难程度。
3.1 确定型多项式空间复杂性确定型多项式空间复杂性(deterministic polynomial space,PSPACE)是指能够被确定型图灵机在多项式空间内解决的问题的集合[19]。属于PSPACE问题举例:全量词化的布尔公式(true qualified boolean formula,TQBF)[6],形如:∀x∃y(x∧y),该公式的含义是:对于任意的x,存在y,使得x∧y为真。全量词化的布尔公式是指公式中出现的所有变量,都有量词对其约束[6]。TQBF问题就是判定一个全量词化的布尔公式是真或假的问题,它属于PSPACE。其多项式空间算法[1]如下:
T=对输入的全量词化的布尔公式:
1)若该公式不含量词,则它是一个只有常数的表达式。计算公式的值,若为真,则接受;否则,则拒绝。
2)若公式等于∃xφ,在φ上递归地调用T,首先用0替换x,然后用1替换x。只要有一个结果是接受,则接受;否则,拒绝。
3)若φ等于∀xφ,在φ上递归调用T,首先用0替换x,然后用1替换x。若2个结果都是接受,则接受;否则,拒绝。
算法分析 该算法模拟的是量词化布尔公式的计算过程,每一次递归就是对公式中最左侧的一个量词所约束的变量赋值(假设该公式为前束范式[18])。递归的深度就是该公式φ中包含的变量的个数,设为m,因此每层只需存储一个变量,所以该算法的空间消耗是O(m)。因此该算法属于多项式空间算法。
3.2 NPSPACE它是指能够被非确定型图灵机在多项式空间内解决的问题的集合。空间与时间不同,它可以被重复使用,根据萨维奇定理[20],如果一台非确定型图灵机能够利用f(n)空间解决某个问题,那么一台确定型图灵机能够在至多f2(n)空间解决相同的问题。由该定理可得推论:NPSPACE=PSPACE[1]。
3.3 PSPACE的完全问题一个语言B属于PSPACE的完全问题[1](PSPACE-complete),如果它满足2个条件:
1)B属于PSPACE;
2)每个属于PSPACE的问题在多项式时间内归约到B。
PSPACE-complete属于PSPACE类中最困难的问题,和NP-complete的定义类似,如果B仅仅满足条件2,说明B不属于PSPACE,可以说它是PSPACE-hard,那么B可能更加难解。常见的属于PSPACE-complete的问题有QBF[6](量词的布尔公式)、formula game[1] (公式博弈)、棋类游戏[1](chess game)等。
举例 广义地理学游戏[1](generalized geography game)是一种地理学游戏,选手们轮流给出世界各地的城市名称。每一座选中的城市的首字母必须与前一座城市的尾字母相同,城市的名称不允许重复,游戏从某个指定的城市开始,直到某一方不能延续为止。对于证明某问题属于PSPACE-complete的过程与NP-complete的证明类似,首先要证明该问题属于PSPACE,文献[1]中给出了一个多项式空间的算法,证明了该问题可在多项式空间求解。然后选择了一个已被证明为PSPACE-complete类的问题如formula game(实际上,它就是TQBF,只是假设有2个选手交替为每个变量赋值)并独出心裁地构造了一个归约,如图 3[1]。
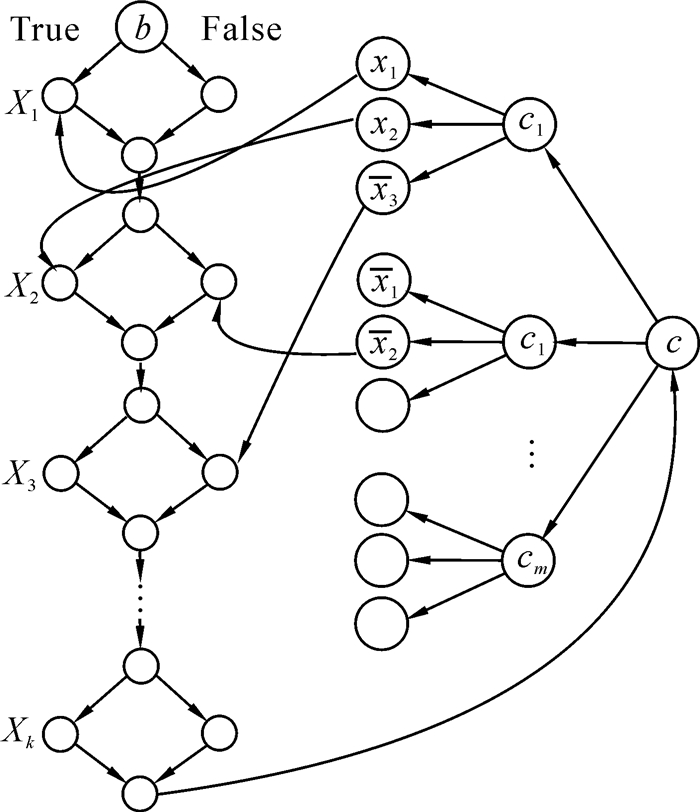
|
| 图 3 归约的全部结构 Fig. 3 The complete structure of reducibility |
这是一个广义地理学的有向图,在该图上模拟进行formula game,设布尔公式为∃x1∀x2∃x3∀x4…∃xk[(x1∨
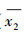

前文介绍了常见的时间复杂性类和空间复杂性类,下面来讨论这些复杂性类中哪个相对简单,哪个相对更加难解。
4.1 P与NP的关系P是在确定型图灵机上以多项式时间求解的问题的集合;NP是在非确定型图灵机上以多项式时间求解的问题的集合;NP问题若在确定型图灵机上求解,就需要用确定型图灵机去模拟非确定型图灵机的运行过程,这种模拟所需要的时间是指数级的,因此,普遍认为NP问题要难于P类问题,即P⊆NP[3]。但是否P=NP,有许多学者都在致力于这方面的研究工作,如果P=NP,那么所有NP问题都能够找到有效的多项式时间算法,也就是说许多难解的问题都可以迎刃而解。但是还没有成功[1],大多数学者还是接受P≠NP[2],COOK[13]证明了第一个属于NP-complete的问题——可满足性问题(satisfiability, SAT),同时根据映射可归约性,在某种意义上,是将所有NP问题归为了同一个问题[2]。这为研究P和NP是否相等的学者们提供了一个方便,即只要证明一个NP-complete问题存在有效的多项式时间算法,那么所有的NP问题都存在多项式时间算法[2]。
4.2 时间复杂性与空间复杂性的关系前面已经提到过,运行快的算法不可能消耗大量的空间,也就是说在每个计算步上最多能访问一个新单元,所以,任何在时间t(n)内运行的机器最多能消耗t(n)的空间[1]。因此空间复杂性类(PSPACE和NPSPACE)的问题要难于时间复杂性(P和NP)类的问题。
4.3 空间复杂性与EXPTIME的关系根据文献[1]中的引理:设M是有q个状态和g个带符号的LBA(一种受限制的图灵机)。对于长度为n的带子,M恰有qngn个不同的格局。可推出,需要空间为f(n)的PSPACE问题,根据渐近记法,最多有f(n)×2O(f(n))个不同的格局,假设处理每个格局需要一个时间单元,在最差的情况下(遍历到第f(n)×2O(f(n))个格局,图灵机输出接受或拒绝,即处于停机状态),求解该问题所用时间等于f(n)×2O(f(n))。即该PSPACE问题必定在时间f(n)×2O(f(n))内运行,因此PSPACE⊆EXPTIME[3]。所以,各个计算复杂性类之间的关系为P⊆NP⊆PSPACE=NPSPACE⊆EXPTIME[1],如图 4。

|
| 图 4 各复杂性类之间的关系 Fig. 4 The relations of some complexities |
计算复杂性是计算理论的一个分支,它是一个理论性很强的计算机科学问题,极具挑战性。通过研究问题的计算复杂性,可以了解该问题求解的难易程度,如果是难解的(如NP-complete、PSPACE-complete),即该问题不存在有效的多项式时间求解算法,则不必将大量的精力放在寻找该问题的有效算法上,从而提高了工作效率。论述了计算理论的一些基本概念,并通过例子论述了各个计算复杂性类的证明方法和当前计算复杂性理论的研究现状。最后详细分析了各个复杂性类之间的关系。在该领域中,还存在一些尚待解决的难题,比如:P是否等于NP,许多学者都在致力于这方面的研究工作,如果P=NP,那么所有NP问题都能够找到有效的多项式时间算法,也就是说许多难解的问题都可以迎刃而解。但是这个等式还没有被成功证明;各个复杂性类之间的包含关系是否正确也有疑问,这些包含关系是否存在着真包含,这些都是国内外学者们今后重点研究的课题。
| [1] | SIPSER M. Introduction to the theory of computation[M]. 2nd ed Beijing: China Machine Press, 2006 : 265 -323. |
| [2] | DASGUPTA S, PAPADIMITRIOU C H, VAZI-RANI U V. Algorithm[M]. New York: McGraw-Hill Science/Engineering/Math, 2006 : 257 -264. |
| [3] | PAPADIMITRIOU C. Computational complexity[M]. Reading, Massachusetts: Addison-Wesley, 1994 : 491 -493. |
| [4] | 朱一清. 可计算性与计算复杂性[M]. 北京: 国防工业出版社, 2006 : 44 -45. |
| [5] | 堵丁柱. 计算复杂性导论[M]. 北京: 高等教育出版社, 2000 : 21 -22. |
| [6] | ARORA S, BARAK B. Computational complexity[M]. New York: Cambridge University Press, 2007 : 24 -85. |
| [7] | 陈志平, 徐宗本. 计算机数学——计算复杂性理论与NPC、NP难问题的求解[M]. 北京: 科学出版社, 2001 : 81 -83. |
| [8] | NP [DB/OL]. [2013-10-17]. http://zh.wikipedia.or-g/wiki/NP. |
| [9] | COPRIME[DB/OL].[2013-10-17]. http://zh.wikiped-ia.org/wiki/COPRIME. |
| [10] | GRAHAM R L, KNUTH D E, PATASHNIK O. Concrete mathematics[M]. Massachusetts: Addison-Wesley, 1989 : 107 -110. |
| [11] | HONSBERGER R. Mathematical gems II[M]. Washington, DC: The Mathematical Association of America, 1976 : 54 -57. |
| [12] | KARP R M. Reducibility among combinatorial problems[Z]. New York: Plenum Press, 1972: 85-103. |
| [13] | COOK S A. The complexity of theorem proving procedures [C]//Proceedings of the Third Annual ACM Symposium on Theory of Computing. New York, USA, 1971: 151-158. |
| [14] | ZHANG Lintao. Searching for truth: techniques for satisfiability of boolean formulas[D]. Princeton: Princeton University, 2003: 10-14. |
| [15] | CORMEN T H, LEISERSON C H, RIVEST R L, et al. Introduction to algorithms[M]. 2nd ed Cambridge, Massachusetts: MIT Press, 2009 : 1108 -1110. |
| [16] | VERTEX COVER [DB/OL]. [2013-10-19].http://zh.wikipedia.org/wiki/VERTEXCOVER. |
| [17] | STOCKMEYER L J, CHANDRA A K. Provably difficult combinatorial games[J]. SIAM J Compuf , 1979, 8 (2) : 151-174 DOI:10.1137/0208013 |
| [18] | 罗森. 离散数学及其应用[M]. 北京: 机械工业出版社, 2011 : 21 -30. |
| [19] | PSPACE[DB/OL].[2013-10-20].http://zh.wikipedia.org/wiki/PSPACE. |
| [20] | SAVITCH W J. Relationships between nondeterministic and deterministic tape complexities[J]. Journal of Computer and System Sciences , 1970, 4 (2) : 177-192 DOI:10.1016/S0022-0000(70)80006-X |



