2. 北京大学 信息科学与技术学院, 北京 100871
2. School of Electronics Engineering and Computer Science, Peking University, Beijing 100871, China
近些年, 科研工作者在群体智能算法的研究中投入了大量精力,提出了许多新型算法和有效改进方式,使得这一领域呈现出欣欣向荣的景象。关于群体智能的定义,存在许多版本,例如:G. Beni和J. Wang指出群体智能是由具有自组织能力的个体通过组合从而表现出群体的行为的特性[1-2]。Bonabeau、Dorigo和Theraulaz在《群体智能——从自然到人工系统》书中指出群体智能是简单的个体通过通信、协作等交互机制表现出群体智能行为[3]。Kennedy等指出群体智能是简单的具有信息处理能力的单元在交互过程中表现出简单个体不具有的能够解决复杂问题的一种能力[4]。Liu等指出群体智能是简单自制的代理单元展现出的集体的智能行为[5]。Krause等指出群体智能是两个或多个个体独立地或者部分独立地获取信息,信息的差异通过个体的交互被组合或处理,然后产生区别于单个个体能够产生的解决方案[6]。总之,群体智能就是简单个体通过协作达到了拥有简单个体不具有的问题解决能力。
在群体智能算法的发展过程中,比较重要的里程碑事件有:1987年,Craig Reynolds提出了一个使用计算机模拟鸟飞行的模型[7];1991年,Dorigo根据对自然界中蚁群觅食这一群体行为的观察研究提出了蚁群优化算法[8];1995年Kennedy和Eberhart根据对鸟群觅食这一群体行为的观察提出了粒子群优化算法[9]。蚁群算法、粒子群优化算法发展过程中表现出强大的问题求解能力将群体智能的研究推向了一个高潮,吸引了大量的科研工作者投入到群体智能领域进行研究。
群体智能算法模拟简单个体通过协作求解复杂问题的过程,具有以下特点[10]:1)组成群体的个体通常行为、能力都较为简单,个体之间无差别;2)个体通过协作完成复杂问题的求解,群体中无中心控制个体。
近年来,群体智能算法的研究内容主要包括:1)已有的群体智能算法性能的提高,比如研究蚁群优化算法、粒子群优化算法的收敛性加速策略、自适应策略等[11-13];2)新型群体智能算法的提出[14];3)多目标群体智能算法研究,目前大部分有影响力的群体智能算法都有了其多目标算法的版本,例如NSGA-II[15]、SPEA-II[16]、NSPSO[17]等;4)并行化群体智能算法研究,比如基于图像处理单元(GPU)的粒子群优化算法[18]、基于GPU的烟花算法[19]、基于GPU的遗传算法[20]等;5)应用研究,尝试将群体智能算法应用到更多更广阔的领域。
自2000年以来,一系列新型群体智能算法相继被提出[14]。在2010年,Tan和Zhu根据对于烟花爆炸产生火花这一自然现象的观察提出了烟花算法。尽管文献[21]对烟花算法的部分研究工作进行了简要总结,但是文献[21]总结的工作较为初步,尤其是近一年来烟花算法的研究工作取得了一些新的进展,因此,本文将对烟花算法进行了全面的综述。
1 烟花算法 1.1 动机燃放烟花爆竹是中国传统节日尤其是除夕的一项重要节日庆祝活动。在这一天,成千上万的烟花爆竹在夜空中爆炸并绽放美丽的图案。通常,在市场上,不同价格的烟花爆炸产生不同的效果。一般价格高昂(低廉)的烟花产生的火花数量比较多(少),爆炸产生的火花分布的范围也较均匀(分散)。受到烟花在夜空中爆炸产生火花并照亮周围区域这一自然现象的启发,Tan和Zhu在2010年提出了烟花算法(FWA)[22]。
点燃的烟花被发射到夜空中,爆炸产生火花继而照亮其临近的夜空,产生出一幅美丽的图案。事实上,一个优化问题的求解过程亦是如此。对于一个最优化问题,尤其自变量是连续空间的最优化问题,在整个解空间内,如何有效迅速地找到全局最优解呢?在烟花算法中,烟花被看作为最优化问题的解空间中一个可行解,那么烟花爆炸产生一定数量火花的过程即为其搜索邻域的过程,如图 1所示。

|
| 图 1 真实的烟花爆炸和优化问题解搜索过程对比示意 Fig. 1 Comparison between fireworks explosion and solution search for optimization problem |
为了能够有效地进行搜索,这里要求解空间中解的邻域有意义,同时需要保证在某一有限的范围内,解和其邻域的其他解具有相似的性质——“靠近是一种性质”[23]。这个要求是烟花算法应用于优化求解的有效性关键,因此在实际使用烟花算法求解优化问题时,在问题建模和解的编码过程中,无论是离散编码还是连续编码都需要满足这一个基本条件。此外,烟花种群中各个烟花根据相对于其他烟花的适应度值进行资源分配和信息交互使得整个种群能够在全局搜索能力和局部搜索能力之间达到一个平衡,而且烟花的爆炸搜索机制使得单个烟花具有很强的局部爆发性。因此,烟花算法中烟花之间进行的资源的交互(爆炸火花数目和爆炸半径)使得烟花算法成为一种新型的群体智能算法。
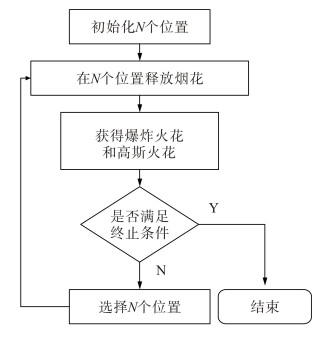
1.2 算法框架烟花算法的算法执行流程如图 2所示。
|
| 图 2 烟花算法执行流程图 Fig. 2 Flowchart of fireworks algorithm |
烟花算法具体包括以下几个步骤:
1)在可行解空间中随机产生一定数量的烟花,每个烟花代表解空间中的一个可行解。
2)根据优化目标函数计算每个烟花的适应度值,并据此确定烟花质量的好坏,以在不同爆炸半径下产生不同数量的火花。在烟花算法中,作者使用了两种形式的火花,分别是爆炸火花和高斯变异火花。其中爆炸火花主要负责对烟花邻近区域的搜索,适应度值好的烟花在较小的邻近区域内产生较多的火花,反之,适应度值差的烟花在较大的邻近区域内产生较少的火花。相对于爆炸火花,高斯火花的引入增强了种群的多样性。
3)判定是否满足终止条件。如果满足则停止搜索,否则在爆炸火花、高斯变异火花和烟花中选择一定数量的个体作为烟花进入下一代的迭代。
烟花算法具有局部搜索能力和全局搜索能力自调节机制。烟花算法中每个烟花的爆炸半径和爆炸火花数是不同的,适应度值差的烟花的爆炸半径较大,使其具有更大的“探索能力”——勘探性。适应度值好的烟花的爆炸半径较小,使其能够在该位置周围具有更大的“挖掘能力”——开采性。此外,高斯变异火花的引入可以进一步增加种群的多样性。文献[24]给出了一个关于烟花的爆炸半径和爆炸火花数目对于烟花算法性能的影响的简要分析。
1.3 算子分析不失一般性,假设待求解的优化问题形式如下:
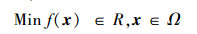 |
(1) |
式中:Ω为解的可行域。
使用烟花算法对优化问题(1)进行求解的目标是在可行域Ω内,寻找一点
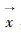
在烟花算法中,爆炸算子(即爆炸产生火花操作)、变异算子(高斯变异产生火花操作)和选择策略(即选择下一代烟花操作)是最重要的3个组成部分,直接决定烟花算法的性能优劣。
1)爆炸算子
在可行域Ω内初始化一定数量烟花,对烟花位置的适应度值进行评估。为了差异化不同位置的烟花,一般适应度值较好(即适应度值较小)的烟花能够获取更多的资源,在较小的范围内产生更多的火花,具有对于该烟花位置的强大的局部搜索能力。反之,适应度值较大的烟花只能获取相对较少的资源,在较大的范围内产生数量较少的火花,具有一定的全局搜索能力。
为了达到烟花差异化的目的,即开采性和勘探性兼顾的目标,在烟花算法中,每个烟花的爆炸半径和爆炸产生的火花数目是根据其相对于烟花种群中其他烟花适应度值计算得到的。对于烟花xi,其爆炸半径Ai和爆炸火花数目Si的计算公式分别为
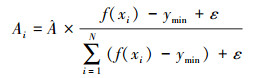 |
(2) |
 |
(3) |
式中:ymin=min(f(xi)),(i=1, 2, …, N)为当前烟花种群中适应度最小值,ymax=max(f(xi)),(i=1, 2, …, N)是当前烟花种群中适应度最大值。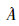
在式(3)中,为了限制适应度值好的烟花位置不会产生过多的爆炸火花,同时适应度值差的烟花位置不会产生过少的火花粒子,文献[22]对于产生的火花个数进行了如下的限制:
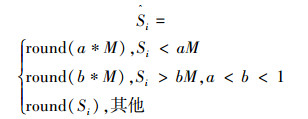 |
(4) |
式中:a、b是两个常数,round( · )是根据四舍五入原则的取整函数。
2)变异算子
为了增加爆炸火花种群的多样性,烟花算法引入了变异算子用于产生变异火花,即高斯变异火花。高斯变异火花产生的过程如下:首先在烟花种群中随机选择一个烟花xi,然后对该烟花随机选择一定数量的维度进行高斯变异操作。对于烟花xi的某一个选择得到的维度k执行高斯变异操作即为
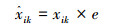 |
(5) |
式中:e~N(1, 1),N(1, 1)表示均值为1,方差为1的高斯分布。
在爆炸算子和变异算子分别产生爆炸火花和高斯变异火花过程中,可能产生的火花会超出可行域Ω的边界范围。当火花xi在维度k上超出边界,将通过式(6)的映射规则映射到一个新的位置。
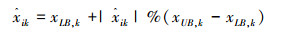 |
(6) |
式中:xUB, k、xLB, k为解空间在维度k上的上边界和下边界。
3)选择策略
为使烟花种群中优秀的信息能够传递到下一代种群中,在产生爆炸火花和高斯变异火花后,算法会在候选者集合(包括烟花、爆炸火花和高斯变异火花)中选择一定数量的个体作为下一代的烟花。
假设候选者集合为K,烟花种群大小为N。候选者集合中适应度值最小的个体会被确定性地选择到下一代作为烟花,而对剩下的N-1个烟花的选择使用轮盘赌的方法在候选者集合中进行选择。对于候选者xi,其被选择概率的计算公式为
 |
(7) |
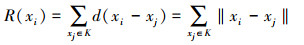 |
(8) |
式中:R(xi)为当前个体到候选者集合K除xi所有的个体之间的距离之和。在候选者集合中,如果个体密度较高,即该个体周围有很多其他候选者个体时,该个体被选择的概率会降低。
基于前面的叙述,烟花算法的具体执行如下:
1)参数初始化
随机在解空间初始化N个位置xi,即N个烟花。
2)循环如下的(1)~(4),直到满足终止条件。
(1)//评估每个烟花适应度值,计算每个烟花爆炸半径和爆炸火花数
fori=1 to N do
计算每个烟花的适应度值f(xi);
计算每个烟花的爆炸半径Ai和产生的爆炸火花数目Si;
endfor
(2)//产生爆炸火花
for i=1 to N do
for j=1 to Si do
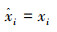
随机选择z个维度作为集合DS,
z=round(D×U(0, 1)),D为xi的维数(U(a, b)表示为在区间[a, b]中产生服从均匀分布的随机数的值);
计算位置偏移
 ;
; |
(1) |
for each kin DS
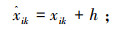 ; ; |
(2) |
越界检测;
endfor
将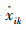
endfor
endfor
(3)//产生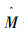
for i =1 to 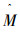
随机选择火花xi;
随机选择z个维度作为集合DS,
z=round(D×U(0, 1)),D为xi的维数;
计算高斯变异参数e=Ν(1,1)(产生矩阵为1,方差为1的随机数);
for each kin DS
 |
(3) |
越界检测;
endfor
将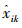
endfor
(4)从烟花、爆炸火花、高斯变异火花种群中选择N个个体作为下一代迭代计算的烟花;
3)返回优化结果。
1.4 与遗传算法、粒子群优化算法搜索机制比较烟花算法相对于遗传算法和粒子群优化算法表现出了不同的搜索机制。在遗传算法中,染色体通常被编码成一个优化问题的解,染色体之间通过交叉和变异操作产生新的解。在编码空间上,子代染色体和父代染色体具有相近的性质。粒子群优化算法通过种群中的粒子间相互协作,每个粒子通过种群中的全局最优信息和自身历史最优信息进行指导搜索,进而更新粒子的位置。对于烟花算法,其主要用于连续空间的优化问题求解,烟花算法采用爆炸搜索机制。此外,烟花之间通过交互机制来计算每个烟花的爆炸半径和爆炸火花数目,使得适应度值较好的烟花获取更多的资源,反之,适应度值较差的烟花获取较少的资源。烟花算法和遗传算法具有一些类似的地方,比如遗传算法可以通过变异概率的大小在“编码空间”中产生一个相对于当前染色体距离较远/近的解[25],而同样地,烟花算法可以通过不同的爆炸半径大/小产生距离烟花较远/近的爆炸火花,烟花算法在迭代过程中,种群中每个烟花个体在一次迭代过程中会产生多个个体,而粒子群优化算法通常只产生一个个体,烟花算法的这种爆炸机制使得其对于烟花附近的区域的搜索更加彻底。
2 几种典型的改进烟花算法烟花算法自提出后就受到了诸多科研工作者的关注,许多改进算法相继被提出。改进烟花算法主要可以被分为两类,一类是在基本烟花算法的基础上进行算子的分析和改进,另一类是与其他启发式算法的混合算法的研究。
第一类算法改进的工作主要有:Pei等[26]提出基于适应度函数估计的加速型烟花算法(AcFWA)。AcFWA使用烟花及其产生的爆炸火花、高斯变异火花种群的位置信息和适应度值信息来估计搜索空间的形状,然后使用估计的形状的最优位置作为启发式信息引入到当前种群进行加速搜索。Liu等[27]提出一种构造型烟花算法(IFWA),使用了一种新型的烟花爆炸半径和爆炸火花数目的计算方式,相对于基本烟花算法,获得了性能上的提升。Zheng S.等[28]对于基本烟花算法的爆炸算子、变异算子、选择策略和映射规则等进行了细致的分析,针对烟花算法存在的缺陷进行了逐一改进,并提出了增强型烟花算法(EFWA)。接着,Zheng S.等[29]和Li等[30]分别提出了两种自适应半径策略——动态搜索烟花算法(dynFWA)和自适应烟花算法(AFWA)。在dynFWA中,烟花爆炸半径的变化过程依据烟花种群产生的火花适应度值是否发生改进(即优化得到适应度值更优的火花)决定。在AFWA中,烟花的爆炸半径的确定依据当前种群适应度值最优的个体和一个特定个体之间的距离计算。这两种方法由于采用了自适应调整爆炸半径的机制,都大大提升了增强型烟花算法的性能。
第2类算法改进的工作有:Zheng Y.等[31]提出使用差分演化算法和烟花算法进行混合的新型算法FWA-DE。Yu等[32]用差分变异替换基本烟花算法中的高斯变异,所提出的FWA-DM算法比EFWA算法的性能更好。Gao等[33]提出使用文化算法和烟花算法进行混合的文化烟花算法(CA-FWA),并将文化烟花算法应用到滤波器的设计上,取得了相对于量子粒子群优化算法(QPSO[34])和自适应量子粒子群优化算法(AQPSO[35])较优的性能。Zheng等[37]将生物地理学优化算法引入增强烟花算法,提出混合算法BBO-FWA,提高了烟花间的交互能力。
2.1 基于适应度函数估计的烟花算法进化计算加速策略研究是一个比较重要的研究方向。1999年,Takagi等[36]提出对于一个简单的单峰优化问题求解,可以通过进化算法优化的解信息去估计搜索空间形状,然后对估计得到的简单曲面求解其最优值位置并引入到种群中作为启发式信息来加速搜索过程。基于此,在烟花算法中,在每一代烟花产生爆炸火花和高斯变异火花以后,Pei等[26]尝试使用当前种群的候选者集合(烟花、爆炸火花和高斯变异火花)的位置信息和适应度值信息去估计整个搜索空间的形状,然后根据估计得到的形状等作为启发式信息。
文献[26]讨论了3种不同的抽样策略:基于适应度值的抽样策略,即在候选者集合中选择k个适应度值最好的样本个体;基于距离的抽样策略,即在候选者集合中选择欧式距离上离最优点位置最近的k个样本个体;随机抽样策略,即随机从候选者集合中选择k个样本个体。对于搜索空间的估计,文献中将D维搜索空间投影到每一个维数上面,并使用抽样得到的样本个体在该维度上的投影位置和适应度值信息依据估计模型进行形状估计。
在实验中,抽样点个数被设置成3、5和10,用于研究抽样点个数对于算法性能的影响。对于通过选择有限的样本点估计其搜索空间形状这一问题,曲面估计形状的选择十分重要。文献中使用一次最小二乘法、二次最小二乘法来研究模型的选择对于性能的影响。
2.2 构造型烟花算法在FWA中,为了差异化不同的烟花,使得适应度值较低的烟花拥有更多的资源,即在较小的爆炸半径内产生较多数量的爆炸火花,同时使得适应度值较高的烟花拥有较少的资源,即在较大的爆炸半径内产生较少数量的爆炸火花。这两类烟花分别对应着局部搜索能力和全局搜索能力,基本烟花算法采用式(2)、(3)计算爆炸半径和爆炸火花数目。
事实上,可以有许多种计算方法使得计算得到的爆炸半径和爆炸火花数目具有上面提到的这一性质。Liu等[27]使用烟花的适应度值的排序信息来计算烟花的爆炸半径和爆炸火花数目,适应度值低的烟花具有较小的序号,反之,适应度值较大的烟花具有较大的序号。除了改进爆炸算子,Liu等[27]还对高斯变异算子和选择策略进行了修改。对于高斯变异算子,Liu等使用了一种随机变异算子产生变异火花;对于选择策略,文中讨论了基于适应度值的轮盘赌选择策略和随机选择策略对性能的影响。
2.3 增强烟花算法Zheng S.等[28]对FWA的算子进行了细致的分析,针对FWA的缺陷进行了改进,包括最小爆炸半径检测、爆炸火花产生方式、映射规则、高斯变异算子和选择策略,提出了增强型烟花算法(EFWA)。
2.3.1 最小爆炸半径检测在FWA中,通过对不同的烟花设置不同的爆炸半径来保持全局搜索和局部搜索的平衡,使得烟花种群具有探索性和开采性。尽管这个想法看似可以通过式(2)达到这一性质,然而,在使用式(2)计算爆炸半径的时候会发现适应度值最小的烟花的爆炸半径非常小,接近于0,从而浪费了宝贵的资源。
为了解决这一缺陷,EFWA引入了最小爆炸半径检测机制。如果烟花的爆炸半径小于某一阈值,则将其置为该值,如式(9):
 |
(9) |
对于如何确定Amin, k,EFWA提出了使用非线性递减方式:
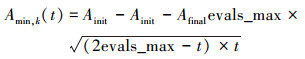 |
(10) |
其中,t指当前函数评估的次数,evals_max为最大函数评估次数。Ainit、Afinal表示迭代过程中的最初和最终爆炸半径检测值。
2.3.2 爆炸火花产生方式在FWA中,烟花爆炸产生火花时在所有选择的维度上爆炸的偏置是相同的。然而,相同的偏置将会降低局部搜索的多样性。为了解决这一问题,EFWA在每个选择的维度上使用不同的偏置值。此外,在EFWA中,爆炸维度的选择亦有不同[28]。
2.3.3 映射规则在FWA中,当一个火花(爆炸火花或高斯变异火花)在维度k上超出边界,会通过式(6)的映射规则映射到一个新的位置。在很多时候,火花位置超出边界通常都是一个较小的值,而且通常使用的测试函数都是边界对称的,即
 |
(11) |
式中:xUB, k、xLB, k为解空间在维度k上的上边界和下边界。那么,在这种情况下,超出边界的火花在维度k上会被映射到一个距离原点很近的位置上。然而,由于很多测试函数的最优值都在原点位置或者附近,因此,这种映射规则会无意地加速算法收敛,而这种加速并不是算法的智能。
为了解决这一缺陷,EFWA提出使用下式作为映射规则来处理超出边界的火花。
 |
(12) |
(式中:xUB, k、xLB, k为可行区域在维度k上的上边界和下边界。
2.3.4 高斯变异算子在FWA中,在产生高斯变异火花时,当随机产生e~N(1, 1),的值接近于0时候,高斯变异火花的计算方法如式(5)所示,位置xik会接近于0,而且很难跳出。此外,如果产生较大的e值,通过FWA的映射规则即式(12)使得xik可能会被映射到原点位置附近。这对于最优值在原点的优化函数来说将极大地加速优化过程的收敛,而对其他最优值不在原点或者其附近的测试函数则浪费了搜索资源。
为了避免这一个缺陷,EFWA使用一种新型高斯变异算子,计算公式为
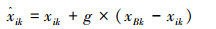 |
(13) |
式中:g~N(0, 1),xBk为当前烟花种群中适应度函数值最小的烟花的第k维度上的位置。
2.3.5 选择策略在FWA中,选择策略是基于距离度量的,由式(7)进行计算。但这种选择方式需要在每一次迭代过程中,计算候选者集合中任意两个个体之间的距离,这是十分耗时的。EFWA使用一种精英随机选择策略,即首先选择出候选者集合中适应度值最小的个体,然后,对其余的烟花的选择采用随机策略。
2.4 动态搜索烟花算法和自适应烟花算法在FWA和EFWA中,烟花算法的爆炸半径由式(2)计算的。在烟花种群中,当烟花的适应度值较低时,该烟花所在的位置被认为是一个潜在较好的区域,应增加在该位置的搜索资源; 对于一个适应度值较高的烟花,所在的位置被认为是一个潜在的较差区域,应减少该位置的搜索资源。
然而,这种爆炸半径计算方法存在很多不合理的地方。比如在烟花种群中,可能烟花刚开始进入一个好的区域并对其进行搜索时,其搜索点的适应度值相对于种群中其他烟花所在的位置的适应度值差。在这种情况下,该点的搜索资源在下一代会被大大降低,以至于即使烟花进入了一个比较好的区域,原先的这种爆炸半径和爆炸火花数计算方法仍然可能导致烟花很难对于一个潜在的好的区域的深度挖掘,即持久性开发。而且,在FWA和EFWA算法中,算法仅根据烟花的适应度值之间的差异来决定爆炸半径和爆炸火花数目,并没有考虑到优化问题求解的过程中的启发式信息。比如,即使最优的烟花达到了一个较好的区域,每次计算其爆炸半径都是根据相对于其他烟花的适应度值信息计算的,但是,如果烟花需要具有强大的局部搜索能力其爆炸半径可能需要降低到非常小的范围内才能够使得有限的资源(即每个烟花的爆炸火花数目)下找到更好的解,而仅根据烟花相对于种群中其他烟花的适应度值计算得到的爆炸半径很难达到非常小的值,因此在测试函数上,FWA和EFWA往往表现出了不太好的局部搜索能力[28]。
2.4.1 动态搜索烟花算法基于前面的分析,Zheng S.等提出了动态搜索烟花算法dynFWA[29]。在dynFWA中,Zheng S.等将烟花种群分为2类:核心烟花(适应度值最优的烟花)和非核心烟花。核心烟花和非核心烟花的区别主要在于:1)核心烟花能够在较小的爆炸半径范围内产生更多的爆炸火花,进行局部搜索,而非核心烟花在较大的爆炸半径范围内产生更少的爆炸火花,进行全局搜索。2)核心烟花由于是适应度值最低的个体,很大概率上核心烟花或者其子代会被选择到下一代。这也就是为什么dynFWA算法中的动态搜索爆炸策略应用到核心烟花上。而非核心烟花并不能保证会被确定地选择到种群的下一代中。
在dynFWA中,核心烟花的爆炸半径依据动态搜索策略进行调整,同时其他非核心烟花仍旧依据式(2)计算。在dynFWA中,当烟花种群中找到了一个适应度值更低的位置,核心烟花的爆炸半径变大,反之,核心烟花的爆炸半径变小。
在dynFWA中,Zheng S.等细致分析了核心烟花的爆炸半径放大缩小机制。当烟花种群搜索得到一个适应度值更低的位置的时候,通常情况下有3种情况:1)核心烟花找到的;2)距离核心烟花位置很近的非核心烟花找到的;3)距离核心烟花位置不近的非核心烟花找到的。在第1种情况下,为了增大收敛速度,更快地找到解空间的全局最优位置,放大爆炸半径是一种最直接有效的方法。这同样适用于第2种情况。在第3种情况下,找到的适应度函数值更低的位置在下一代会被选择为核心烟花,其爆炸半径应该重新初始化。然而,由于动态搜索策略具有自适应调整爆炸半径的能力,而且很难有简单有效的距离度量方式表明距离当前的核心烟花很远,所以为了简便,在dynFWA中,下一代核心烟花的爆炸半径仍然被放大。
当烟花种群搜索不到一个适应度值更好的位置的时候,dynFWA将缩小核心烟花的爆炸半径。因为缩小爆炸半径将提高找到更优位置的概率[29]。
此外,dynFWA算法相对于EFWA和FWA算法,去除了高斯变异算子使得其时间消耗相对较低。
2.4.2 自适应烟花算法自适应烟花算法(AFWA)是Li等[30]提出的另一种自动调整爆炸半径大小的方法。在AFWA中,候选者集合中的最优个体(下一代的烟花)会被选择到下一代,其爆炸半径的计算方法为选择满足如下两个条件的个体,用最优个体和该个体之间的距离作为最优个体下一次的爆炸半径:
1)该个体的适应度值比上代的烟花差;
2)该个体是满足条件1)的个体中距离最优个体最近的。
理论分析表明,这种方式能够有效地根据搜索的情况来自适应地调整步长:在初始阶段,这种半径能够自动根据局部区域的大小进行调整;而在局部搜索中它又能够像dynFWA一样根据搜索的结果对步长进行放缩;最后在微调阶段,它会使半径逐渐减小从而找到极值点。因此,AFWA表现出了很好的性能改善。
2.5 差分演化—烟花混合算法在文献[31]中,Zheng Y.等提出了将烟花算法和差分演化算法进行混合的一种新型算法(FWA-DE)。在基本烟花的基础上中,该算法引入了差分演化算法中的变异算子、交叉算子和选择算子。FWA-DE将候选者集合(烟花、爆炸火花和高斯变异火花)按照适应度值升序排列,并从前2P的候选者中选择P个组成集合S。选择方法是首先选择适应度值最小的候选者加入到集合S中,其余P-1个候选者的选择方式依据适应度函数值的轮盘赌选择,对于候选者xi的选择概率计算公式为
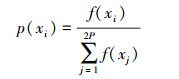 |
(14) |
式中:f(xi)为当前候选者xi的适应度值。这里需要指出,这种选择方式其实是存在风险的,因为在文献中使用的测试函数的最优解都是大于零的,所以计算得到的概率p(xi)恒为正。对于得到的集合S,对集合S中的每个元素执行以下的操作,使用差分进化策略进行迭代进化,包括变异算子、交叉算子和选择算子。
此外,Yu等[32]也尝试用差分变异算子替换烟花算法的高斯变异算子提出了FWA-DM。在基本烟花算法执行过程中,首先在可行解空间随机初始化5D个烟花(D为维度),并评估烟花的适应度值。烟花的爆炸半径根据式(2)计算。每个烟花在爆炸半径内随机产出一个爆炸火花。然后,对比烟花和火花,选择适应度值较低的个体组成新种群,最后,运用变异算子对新种群进行变异。在变异算子的作用下,每个烟花将产生变异火花。对比变异火花和当前火花,适应度值较优的个体被选择到下一代作为烟花。算法迭代进行直到满足终止条件。
2.6 文化-烟花混合算法文化烟花算法(CA-FWA)是Gao等提出的一种用于数字滤波器设计的烟花算法[33]。CA-FWA不同于FWA,其具有4种火花生成的方式。此外,在选择策略上,文化烟花算法的采用的选择策略是首先选择排名靠前的λN个烟花(N是烟花个数),对于剩下的(1-λ)N个烟花的选择策略为在由xi, (i=λN+1, λN+2, …, N)组成的集合中依据FWA算法选择策略进行选择。
2.7 生物地理学优化-烟花混合算法Zhang等[37]将生物地理学优化(BBO)算法和增强烟花算法(EFWA)进行混合——BBO-FWA,提高了烟花之间的交互能力。BBO提供了一种根据个体的适应度值,以概率将个体的某些维的值进行交叉迁移的方法。
在BBO中,个体的适应度值越差,其从别的个体接受某些位置的概率越高,而把自己的某些位置给予别的个体的概率越低,反之亦然。在BBO-FWA,烟花产生爆炸火花的步骤被修改成以概率p进行BBO方式的迁移,以概率1-p产生爆炸火花。p如果较大,能够提升种群的多样性以及个体之间的信息交互,但是对于最优点处于狭缝中的那些评估函数,则是这一概率较小为好。
2.8 改进型单目标烟花算法性能为了验证改进型烟花算法的有效性,通常,对于算法的性能验证主要是通过在测试函数集合测试算法性能或者将改进型烟花算法和基本烟花算法应用到实际优化问题,根据求解结果的质量进行验证。在使用测试函数集合进行性能验证时,目前存在一些标准的测试函数集合,在改进型烟花算法中使用的主要有如下3个标准测试函数集合:
CEC2005,包含25个测试函数[38];
CEC2013,包含28个测试函数[39];
CEC2014,包含30个测试函数[40]。
在测试函数集合上进行性能测试,对于不同算法之间的性能比较主要有比较均值,其中也有适应度值排名等指标[39-40]。为了验证不同算法在测试函数上的差异显著性,通常使用t检验或者Wilcoxon符号秩检验,其中Wilcoxon符号秩检验不假设数据服从正态分布[41]。
3 多目标烟花算法多目标优化算法自20世纪90年代发展,如今大部分有影响力的群体智能算法、进化算法都有其多目标算法版本,例如NSGA-II[15],SPEA-II[16],NSPSO[17]等。相对于单目标优化算法,多目标优化算法应用求解具有多个优化目标的优化问题而不是单个优化目标问题,在实际优化问题中具有更重要的意义。在文献[44]中,Zheng Y.等基于单目标差分演化-烟花混合算法[31](FWA-DE)首次提出多目标烟花算法MOFWA,并将多目标烟花算法应用到油料作物生产这一实际的优化问题中。
在将单目标群体智能算法框架移植去解决多目标优化问题需要解决几个关键步骤:主要包括适应度值计算方法和档案维护方法。
MOFWA使用的SPEA-II[16]方法中的适应度值计算方法。在SPEA-II方法中,对于当前种群中,无论是支配解还是非支配解,其解的强度值是由这个解支配其他解的数目和这个解的浓度决定的。关于档案维护方法,MOFWA使用文献[45]提出的档案维护方法。在档案更新过程中,首先确定支配关系,移除被支配的解,如果仍旧达到档案大小的上限则移除距离最近的一对点中的一个。
MOFOA执行流程如下:首先,初始化N个烟花,每个烟花产生爆炸火花和高斯变异火花。然后,使用产生的火花(包括爆炸火花、高斯变异火花)更新档案。从烟花和火花中选择一定数量的个体组成一个新的群体P,对于P中的每个个体分别执行变异算子、交叉算子和选择算子得到新的群体P′作为下一代烟花算法的种群。算法迭代执行直到满足终止条件。
| 年份 | 算法名称 | 算法改进思想与机制 | 性能验证 | 对比算法及性能 |
| 2010 | FWA | — | 11个函数组 成测试集合 |
对比了CPSO[42]、SPSO[43],在 函数优化结果的均值上FWA 具有更优的性能 |
| 2011 | CA-FWA | 文化算法和烟花算法混合,改变了烟花 算法中爆炸火花产生方式和选择策略 |
滤波器设计 优化问题 |
对比了AQPSO[34]和QPSO[35] 算法,具有更优的性能 |
| 2012 | AcFWA | 利用候选者集合中的位置信息和适应度 值信息估计搜索空间形状,生成精英解, 引入到烟花种群作为启发式信息。 |
CEC2005前 10个函数 |
对于FWA,t检验显示改进有 效 |
| 2012 | FWA-DE | 差分演化算法和烟花算法混合 | 由6个函数 组成的测试 集合 |
对比了FWA、DE,对比算法 优化最优解的成功率,显示 改进有效 |
| 2013 | IFWA | 根据烟花算法思想,适应度值好的烟花 在更小的爆炸半径内产生更多的爆炸火 花,IFWA引入一种新型的爆炸半径和爆 炸火花数目计算方式。 |
CEC2005前 14个函数 |
对比了FWA、PSO算法,在函 数优化结果的均值上IFWA 具有更优的性能 |
| 2013 | EFWA | 细致分析了烟花算法的算子,并针对算 子存在的缺陷提出了相应的改进策略。 |
由12个函数 组成的测试 集合 |
对比了FWA、SPSO算法,t检 验结果显示对于FWA算法 改进有效,EFWA算法相对于 SPSO2007算法局部搜索能力 不佳 |
| 2014 | dynFWA | 针对适应度值最优的烟花引入了动态搜 索爆炸半径策略。 |
CEC2013 | 对比了EFWA算法,Wilcoxon 符号秩检验显示对EFWA算 法改进有效。对比了SP- SO2011算法,dynFWA平均均 值排名更优 |
| 2014 | AFWA | 针对适应度值最优的烟花引入自适应爆 炸半径策略。 |
CEC2013 | 对比了EFWA算法,t检验显 示对EFWA算法改进有效。 对比了SPSO2011、SPSO2007 算法,AFWA平均均值排名更 优 |
| 2014 | FWA-DM | 差分演化算法和烟花算法混合 | CEC2014 | — |
| 2014 | BBO-FWA | 生物地理学优化算法和烟花算法混合 | 由13个函数 组成的测试 集合 |
对比了EFWA、BBO算法,在 函数优化结果的均值上BBO- FWA具有更优的性能 |
4 基于GPU的并行烟花算法
由于群体智能算法在迭代过程中需要不断地根据算法规则迭代产生新的解,时间消耗较大。近些年来,随着并行技术的不断发展,很多群体智能算法,比如粒子群优化算法[9]、遗传算法[46]、差分进化算法[47]等,均有学者开始研究算法的并行版本,烟花算法亦是如此。Ding等[19]2013年在FWA的基础上提出了基于GPU平台的并行烟花算法(GPU-FWA)。
将群体智能算法并行化的核心目标是在保证性能的基础上提高时间加速比,即并行化群体智能算法和串行化群体智能算法的时间消耗对比。而提高加速比的核心策略是使得串行群体智能算法的每个步骤能够最大化地并行化,即如果串行群体智能算法的某个步骤可以并行化则直接将该步骤并行化实现,如果串行群体智能算法的某个步骤由于存在和其他地方的数据交互,则尽可能在性能不降低的情况下修改该算子,提高其并行化程度。
为了降低FWA中烟花之间的交互,Ding等使用了一种新型的爆炸火花产生方法。在FWA中,每个烟花需要和其他烟花进行交互才能够计算出爆炸半径,但是如果每代都进行交互则并行化程度会大大降低。因此,Ding等使用间隔性交互方式,即间隔一定迭代次数后再进行交互计算烟花爆炸半径。在不交互的阶段,每个烟花独立地根据现有的爆炸半径来产生爆炸火花,在GPU-FWA中,爆炸火花数目设置为固定值。
5 应用群体智能算法因其强大的问题求解能力被应用到诸多领域。FWA自提出后,很多学者尝试将其应用到各自领域优化问题求解中。主要应用领域有方程组求解[48]、0/1背包问题[49]、桁架结构质量最小化[50]、非负矩阵分解(NMF)计算[51]、图像识别[52]、垃圾电子邮件检测[53]、滤波器设计[33]、配电网重构优化[54]、施肥问题求解[44],选择性谐波消除的问题[55]多个领域,取得了十分明显的应用效果。
5.1 非负矩阵分解1999年,Lee和Seung提出了著名的非负矩阵分解(NMF)算法[56]。NMF算法使用低秩、非负矩阵W、H对目标矩阵A进行近似,即A≈WH。NMF是一个非线性优化函数,形式如下:
 |
(15) |
式中: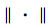
在NMF计算过程中,Janecek等提出基于群体智能算法(包括粒子群优化算法[9]、遗传算法[46]、鱼群算法[57]、差分演化算法[47]和烟花算法[22])的两种NMF计算优化策略[51, 58-59],分别为基于群体智能算法的NMF初始化策略和基于群体智能算法的NMF迭代优化策略。
为了验证策略1的有效性,Janecek等在人工数据集合上进行性能比较,当NMF计算的秩比较小的时候,FWA表现出了较其他算法较差的性能;当NMF计算的秩变大的时候,FWA算法的性能明显提高。为了验证策略2的有效性,Janecek等在人工数据集合上进行性能比较,实验发现策略2对于NMF计算的性能改进十分明显,尤其是在秩比较低的时候,此外,实验结果表明对于策略2不同的群体智能算法之间差异不明显。
5.2 图像识别在图像识别领域,特征之间的距离度量方法对于识别准确率的影响至关重要。在生物特征尤其是线条状的生物特征提取方法中,目前基于方向编码特征提取方法效果较优。在方向性特征提取方法中典型的有竞争编码算法[60], 掌纹方向编码[61]和鲁棒线方向编码[62]。对于这几种特征提取方法的距离度量方法主要有汉明距离和角度距离方法。
在文献[52]中,Zheng S.和Tan细致讨论了汉明距离、角度距离之间的关系,据此提出了一种统一距离作为距离度量方法。
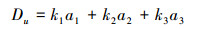 |
(16) |
式中:ki表示特征之间具有i个方向差异的错判代价,ai表示特征之间具有i个方向差异的个数。
相对于文献[63]讨论的统计距离方法,Zheng S.和Tan指出角度距离度量方法的性能并不一定恒差于汉明距离度量方法,即k1≤k2≤k3并不一定恒成立。为了计算得到最优的参数组,Zheng S.等使用粒子群优化算法[43]、差分演化算法[47]和烟花算法[22]进行参数优化。在3个测试集合(人工数据集、掌纹数据集和手指静脉数据集)上面进行实验验证。关于特征提取方法,文中使用了竞争编码算法、掌纹方向编码和鲁棒线方向编码3种特征提取方法。实验结果表明采用群体智能优化算法进行优化的距离度量方法能够显著降低EER值。
5.3 滤波器设计目前,有不少学者将群体智能算法应用到滤波器设计中。Gao等[33]提出使用文化烟花算法CA-FWA进行滤波器的设计,并对比了PSO[64]、QPSO[34]和AQPSO[35]。实验结果表明,基于文化烟花算法(CA-FWA)设计的数字滤波器比使用PSO、QPSO和AQPSO设计的滤波器性能更好。
5.4 垃圾电子邮件检测He等[53]提出使用烟花算法对基于局部免疫浓度特征提取方法和支持向量机分类方法进行垃圾电子邮件检测模型中的参数进行优化。实验结果表明,基于烟花算法优化得到的模型可以获得更高的准确率和F值,展示了烟花算法的优化能力。
5.5 施肥问题在农业耕作中,油料作物生长时的不同肥料的施肥比例对于油料作物的生长至关重要。在油料作物的施肥过程中,需要考虑作物产量、肥料的成本、油料作物的品质、土壤的残余生产能力等一系列指标,因此,油料作物的施肥比例计算问题是一个多目标优化问题。
在第4节中简述了Zheng Y.等提出的多目标烟花算法(MOFWA)。在文献[44]中,Zheng Y.等使用MOFWA进行施肥比例的计算。为了评估多目标烟花算法的性能,文献[44]在3类油料作物的施肥问题上进行了计算,分别是油菜、橄榄和茶油。其中,油菜的施肥问题需要考虑氮磷2种元素,橄榄和茶油需要考虑氮磷钾3种元素。对于优化结果的评价指标,文献中采用了:1)CPU运行时间;2)HyperVolume [65];3)覆盖度量[65]。
在油菜和橄榄这两种作物的施肥优化问题上,实验结果表明当问题规模比较小的时候,所有的算法(NSGA-II[15]、DEMOC[66]、PDE[67]、NSPSO[17]、MOFWA[44])几乎都能够得到相同的帕累托前端,而MOFWA会显得比其他算法多消耗时间。但是, 当问题规模变大后,MOFWA的表现比其他算法好。在茶油施肥问题上,Zheng Y.等对比了MOFWA算法和多目标随机搜索算法(MORS[68])算法,结论是MOFWA的结果能够支配MORS的结果,同时根据人工的经验,MOFWA优化得到的解的质量要高于MORS的结果。
5.6 配电网方案重构Mohamed和Knowsalya[54]提出使用烟花算法进行配电网方案的优化计算。在配电网优化问题中,优化目标为尽量减少电量损耗同时使得电压偏差尽量低。在该优化问题中,解被编码为开转换向量。
为了验证烟花算法的优化配电网方案的有效性,作者在包含33-总线和119-总线的IEEE测试系统上进行实验,实验分为常规情景实验和3种非常规情景实验。结果表明,烟花算法在常规情景下相对于遗传算法[69]、改进遗传算法[70]、改进禁忌搜索算法[71]、和谐搜索算法[72]具有更优的性能,同时在3种非常规情境下得到的优化结果是可以接受的。
6 未来发展方向根据研究和分析,烟花算法的未来研究工作需要在下面几个方向进行深入研究:
1)爆炸算子搜索机制的深入分析。烟花算法相对于其他典型的群体智能算法,如粒子群优化算法等,展现了一种新型的爆炸搜索机制,具有爆发性。怎样更好地将这种爆炸搜索机制应用到其他群体智能算法或应用问题建模求解上有待更深入的研究。
2)烟花交互机制研究。在烟花算法中,算法通过适应度值进行交互,包括爆炸火花数目和爆炸半径的计算。然而,dynFWA和AFWA的提出表明目前这种交互机制不是十分有效。dynFWA和AFWA算法性能的提升主要归结于适应度值最优的烟花的局部搜索能力加强,而种群中的烟花之间的交互机制并没有变化。因此,更有效的烟花交互机制亟待研究。
3)多目标烟花算法研究。目前,对于烟花算法的多目标研究工作并不多,而且在标准多目标测试集合上与其他典型多目标进化计算方法的比较还没有系统地开展。此外,烟花算法不同于其他群体智能算法,其典型爆炸搜索机制会使得烟花在其周围区域产生大量的爆炸火花,因此,需要研究和烟花算法契合的档案维护策略、适应度值计算方法等。
4)并行烟花算法研究。目前,对于并行化烟花算法的研究工作仅限于基本烟花算法,而烟花算法改进工作不断涌现,不同的改进算法对于并行化的研究工作提出了不同的要求。因此,对于特定的性能优异的烟花算法的并行化仍需投入精力。
5)扩展烟花算法求解的问题类型,使得烟花算法能够求解包括动态优化问题、约束优化问题、离散优化问题、自变量为离散连续混合变量的优化问题。因此,怎样依据连续烟花算法思想提出有效的求解不同类型优化问题的新型烟花算法是非常重要的。
6)应用拓展。将烟花算法应用到更广阔的领域,研究和挖掘烟花算法相对于其他群体智能算法所特有的在解决某些问题的自身固有优势。
7 结束语烟花算法自2010年提出之来,诸多研究者已经相继提出了一系列的改进算法。与此同时,多目标烟花算法和基于GPU的并行烟花算法扩展了烟花算法的研究领域,进一步地丰富了烟花算法的研究内容,使得烟花算法能够解决更多类型的优化问题。此外,烟花算法作为一种新型的群体智能算法,在诸多领域的实际优化问题应用中取得了十分优异的效果,展现了其强大的问题求解能力。本文详细给出了到目前为止,烟花算法的研究现状和应用情况,并指明了其未来发展的方向。烟花算法相对于其他群体智能算法展现出了一种新型的爆炸搜索机制,具有其潜在的独特的优势,是一种十分具有潜力的群体智能算法,亟待更多的科研人员参与进来投入精力开展深入细致的研究。
为了方便感兴趣的读者获取我们有关烟花算法的已有和最新研究成果,并下载相应的算法源代码,请访问我们的烟花算法研究网站主页:http://www.cil.pku.edu.cn/research/fwa/index.html
致谢
在本稿形成过程中,北京大学计算智能实验室余超、李骏之、丁科等对于论文修改给出了许多建议和帮助,在这里表示感谢。
| [1] | BENI G, WANG J. Swarm intelligence in cellular robotic systems[C]//Proceedings of NATO Advanced Workshop on Robots and Biological Systems. 1989: 75-80. |
| [2] | BENI G, WANG J. Swarm intelligence in cellular robotic systems[C]// Berlin: Springer, 1993: 703-712. |
| [3] | BONABEAU E, DORIGO M, THERAULAZ G. Swarm intelligence: from natural to artificial systems[M]. New York: Oxford University Press, 1999 : 1 -15. |
| [4] | KENNEDY J, EBERHART R C. Swarm intelligence[M]. Morgan Kaufmann: 2001 : 504 -512. |
| [5] | LIU Y, PASSINO K M. Swarm intelligence: literature overview[J]. Journal of Ohio State University , 2000 : 1-9 |
| [6] | KRAUSE J, RUXTON G D, KRAUSE S. Swarm intelligence in animals and humans[J]. Trends in Ecology & Evolution , 2010, 25 (1) : 28-34 |
| [7] | REYNOLDS C W. Flocks, herds and schools: a distributed behavioral model[J]. ACM SIGGRAPH Computer Graphics , 1987, 21 (4) : 25-34 DOI:10.1145/37402 |
| [8] | COLORNI A, DORIGO M, MANIEZZO V. Distributed optimization by ant colonies[C]//Proceedings of the First European Conference on Artificial Life. Paris, 1991: 134-142. |
| [9] | KENNEDY J, RUSSELL E.Particle swarm optimization[C]//Proceedings of IEEE International Conference on Neural Networks. Perth, WA, 1995: 1942-1948. |
| [10] | ENGELBRECHT A P. Fundamentals of computational swarm intelligence[M]. John Wiley & Sons, 2006 : 15 -28. |
| [11] | DORIGO M, BIRATTARI M, STUTZLE T. Ant colony optimization[J]. IEEE Computational Intelligence Magazine , 2006, 1 (4) : 28-39 DOI:10.1109/MCI.2006.329691 |
| [12] | LIANG J J, QIN A K, SUGANTHAN P N, et al. Comprehensive learning particle swarm optimizer for global optimization of multimodal functions[J]. IEEE Transactions on Evolutionary Computation , 2006, 10 (3) : 281-295 DOI:10.1109/TEVC.2005.857610 |
| [13] | ZHAN Z H, ZHANG J, LI Y, et al. Adaptive particle swarm optimization[J]. IEEE Transactions on Systems, Man, and Cybernetics, Part B: Cybernetics , 2009, 39 (6) : 1362-1381 DOI:10.1109/TSMCB.2009.2015956 |
| [14] | XING B, GAO W J. Innovative computational intelligence: a rough guide to 134 clever algorithms[M]. Springer, 2014 : 250 -260. |
| [15] | DEB K, PRATAP A, AGARWAL S, et al. A fast and elitist multiobjective genetic algorithm: NSGA-II[J]. IEEE Transactions on Evolutionary Computation , 2002, 6 (2) : 182-197 DOI:10.1109/4235.996017 |
| [16] | LAUMANNS M. SPEA2: Improving the strength pareto evolutionary algorithm[J]. TIK-Report , 2001 (103) : 1-21 |
| [17] | LI X. A non-dominated sorting particle swarm optimizer for multiobjective optimization[C]//Genetic and Evolutionary Computation—GECCO 2003. Berlin: Springer, 2003: 37-48. |
| [18] | ZHOU Y, TAN Y. GPU-based parallel particle swarm optimization[C]//IEEE Congress on Evolutionary Computation. 2009: 1493-1500. |
| [19] | DING K, ZHENG S, TAN Y. A GPU-based parallel fireworks algorithm for optimization[C]//Proceeding of the Fifteenth Annual Conference on Genetic and Evolutionary Computation Conference. ACM, 2013: 9-16. |
| [20] | LI J, WANG X, HE R, et al. An efficient fine-grained parallel genetic algorithm based on GPU-accelerated[C]//International Conference on IFIP, Network and Parallel Computing Workshops. Liaoning, China, 2007: 855-862. |
| [21] | TAN Y, YU C, ZHENG S, et al. Introduction to fireworks algorithm[J]. International Journal of Swarm Intelligence Research , 2013, 4 (4) : 39-70 DOI:10.4018/IJSIR |
| [22] | TAN Y, ZHU Y. Fireworks algorithm for optimization[C]// Berlin: Springer, 2010: 355-364. |
| [23] | HASTIE T, TIBSHIRANI R, FRIEDMAN J, et al. The elements of statistical learning: data mining, inference and prediction[J]. The Mathematical Intelligencer , 2005, 27 (2) : 83-85 |
| [24] | LIU J, ZHENG S, TAN Y. Analysis on global convergence and time complexity of fireworks algorithm[C]//2014 IEEE Congress on Evolutionary Computation (CEC).Beijing, China, 2014: 3207-3213. |
| [25] | EBEHART R C, SHI Y. Comparison between genetic algorithms and particle swarm optimization[C]// Berlin: Springer, 1998: 611-616. |
| [26] | PEI Y, ZHENG S, TAN Y, et al. An empirical study on influence of approximation approaches on enhancing fireworks algorithm[C]//IEEE International Conference on Systems, Man, and Cybernetics. Seoul, South Korea, 2012: 1322-1327. |
| [27] | LIU J, ZHENG S, TAN Y. The improvement on controlling exploration and exploitation of firework algorithm[M]. Advances in Swarm Intelligence Berlin: Springer, 2013 : 11 -23. |
| [28] | ZHENG S, JANECEK A, TAN Y. Enhanced fireworks algorithm[C]//2013 IEEE Congress on Evolutionary Computation. Cancun, Mexico, 2013: 2069-2077. |
| [29] | ZHENG S, JANECEK A, LI J, et al. Dynamic search in fireworks algorithm[C]//2014 IEEE Congress on Evolutionary Computation. Beijing, China, 2014: 3222-3229. |
| [30] | LI J, ZHENG S, TAN Y. Adaptive Fireworks Algorithm[C]//2014 IEEE Congress on Evolutionary Computation. Beijing, China, 2014: 3214-3221. |
| [31] | ZHENG Y J, XU X L, LING H F, et al. A hybrid fireworks optimization method with differential evolution operators[J]. Neurocomputing , 2012 (148) : 75-80 |
| [32] | YU C, KELLEY L, ZHENG S, et al. Fireworks algorithm with differential mutation for solving the CEC 2014 competition problems[C]//2014 IEEE Congress on Evolutionary Computation. [S.l.]: [s.n.], 2014: 3238-3245. |
| [33] | GAO H, DIAO M. Cultural firework algorithm and its application for digital filters design[J]. International Journal of Modelling, Identification and Control , 2011, 14 (4) : 324-331 DOI:10.1504/IJMIC.2011.043157 |
| [34] | FANG W, SUN J, XU W, et al. FIR digital filters design based on quantum-behaved particle swarm optimization[C]//International Conference on Innovative Computing, Information and Control. 2006: 615-619. |
| [35] | FANG W, SUN J, XU W. FIR filter design based on adaptive quantum-behaved particle swarm optimization algorithm[J]. Systems Engineering and Electronics , 2008, 30 (7) : 1378-81 |
| [36] | IUGU T, TAKAGI H. Accelerating a GA convergence by fitting a single-peak function[C]//1999 IEEE International Conference on Fuzzy System. Seoul, South Korea, 1999: 1415-1420. |
| [37] | ZHANG B, ZHANG M X, ZHENG Y J. A hybrid biogeography-based optimization and fireworks algorithm[C]//2014 IEEE Congress on Evolutionary Computation. [S.l.]: [s.n.], 2014: 3200-3206. |
| [38] | SUGANTHAN P N, HANSEN N, LIANG J J, et al. Problem definitions and evaluation criteria for the CEC 2005 special session on real-parameter optimization[R]. 2005, 2005005. |
| [39] | LIANG J J, QU B Y, SUGANTHAN P N, et al. Problem definitions and evaluation criteria for the cec 2013 special session on real-parameter optimization[R]. Computational Intelligence Laboratory, 2013, 201-212. |
| [40] | LIANG J J, QU B Y, SUGANTHAN P N. Problem definitions and evaluation criteria for the CEC 2014 special session and competition on single objective real-parameter numerical optimization[J]. Nanyang Technological University , 2013 : 1-50 |
| [41] | WILCOXON F. Individual comparisons by ranking methods[J]. Biometrics Bulletin , 1945 : 80-83 |
| [42] | TAN Y, XIAO Z M. Clonal particle swarm optimization and its applications[C]//IEEE Congress on Evolutionary Computation. [S.l.]: [s.n.], 2007: 2303-2309. |
| [43] | BRATTON D, KENNEDY J. Defining a standard for particle swarm optimization[C]//IEEE Swarm Intelligence Symposium. Honolulu, HI, 2007: 120-127. |
| [44] | ZHENG Y J, SONG Q, CHEN S Y. Multiobjective fireworks optimization for variable-rate fertilization in oil crop production[J]. Applied Soft Computing , 2013, 13 (11) : 4253-4263 DOI:10.1016/j.asoc.2013.07.004 |
| [45] | HAJECK J, SZOLLOS A, šISTEK J. A new mechanism for maintaining diversity of Pareto archive in multi-objective optimization[J]. Advances in Engineering Software , 2010, 41 (7) : 1031-1057 |
| [46] | GOLDBERG D E. Genetic algorithms in search, optimization, and machine learning[M]. Reading Menlo Park: Addison-Wesley, 1989 : 412 . |
| [47] | STORN R, PRICE K. Differential evolution-a simple and efficient heuristic for global optimization over continuous spaces[J]. Journal of Global Optimization , 1997, 11 (4) : 341-359 DOI:10.1023/A:1008202821328 |
| [48] | 杜振鑫. 烟花算法求解非线性方程组[J]. 现代计算机 , 2013 (3) : 18-21 DU Zhenxin. Fireworks algorithm for solving nonlinear equations[J]. Modern computer , 2013 (3) : 18-21 |
| [49] | 张家琴. 求解0/1背包问题的烟花算法研究[J]. 武汉工程职业技术学院学报 , 2011, 23 (3) : 64-66 ZHANG Jiaqin. Fireworks algorithm for solving 0/1 knapsack problems[J]. Journal of Wuhan Engineering Institute , 2011, 23 (3) : 64-66 |
| [50] | PHOLDEE N, BUREERAT S. Comparative performance of meta-heuristic algorithms for mass minimisation of trusses with dynamic constraints[J]. Advances in Engineering Software , 2014, 75 : 1-13 DOI:10.1016/j.advengsoft.2014.04.005 |
| [51] | JANECEK A, TAN Y. Swarm intelligence for non-negative matrix factorization[J]. International Journal of Swarm Intelligence Research , 2011, 2 (4) : 12-34 DOI:10.4018/IJSIR |
| [52] | ZHENG S, TAN Y. A unified distance measure scheme for orientation coding in identification[C]//2013 International Conference on Information Science and Technology. Yangzhou, China, 2013: 979-985. |
| [53] | HE W, MI G, TAN Y. Parameter optimization of local-concentration model for spam detection by using fireworks algorithm[C]//Advances in Swarm Intelligence. Berlin: Springer, 2013: 439-450. |
| [54] | MOHAMED I A, KOWSALYA M. A new power system reconfiguration scheme for power loss minimization and voltage profile enhancement using fireworks algorithm[J]. International Journal of Electrical Power & Energy Systems , 2014, 62 : 312-322 |
| [55] | RAJARAM R, PALANISAMY K, RAMASAMY S, et al. Selective harmonic elimination in PWM inverter using fire fly and fire works algorithm[J]. International Journal of Innovative Research in Advanced Engineering , 2014, 8 (1) : 55-62 |
| [56] | LEE D D, SEUNG H S. Learning the parts of objects by non-negative matrix factorization[J]. Nature , 1999, 401 (6755) : 788-791 DOI:10.1038/44565 |
| [57] | BASTOS C J, DE LIMA N F, LINS A J, et al. Fish school search[M]. Nature-inspired Algorithms for Optimization Berlin: Springer, 2009 : 261 -277. |
| [58] | JANECEK A, TAN Y. Using population based algorithms for initializing nonnegative matrix factorization[M]. Berlin: Springer, 2011 : 307 -316. |
| [59] | JANECEK A, TAN Y. Iterative improvement of the multiplicative update nmf algorithm using nature-inspired optimization[C]//2011 Seventh International Conference on Natural Computation.Shanghai, China, 2011: 1668-1672. |
| [60] | KONG A W K, ZHANG D. Competitive coding scheme for palmprint verification[C]//Proceedings of the 17th International Conference on Pattern Recognition. Cambridge, UK, 2004: 520-523. |
| [61] | JIA W, HUANG D S, ZHANG D. Palmprint verification based on robust line orientation code[J]. Pattern Recognition , 2008, 41 (5) : 1504-1513 DOI:10.1016/j.patcog.2007.10.011 |
| [62] | WU X, WANG K, ZHANG D. Palmprint authentication based on orientation code matching[C]//Audio-and Video-Based Biometric Person Authentication. Berlin: Springer, 2005: 555-562. |
| [63] | GUO Z, ZUO W, ZHANG L, et al. A unified distance measurement for orientation coding in palmprint verification[J]. Neurocomputing , 2010, 73 (4) : 944-950 |
| [64] | CHEN S, LUK B L. Digital IIR filter design using particle swarm optimisation[J]. International Journal of Modelling, Identification and Control , 2010, 9 (4) : 327-335 DOI:10.1504/IJMIC.2010.033208 |
| [65] | ZITZLER E, DEB K, THIELE L. Comparison of multiobjective evolutionary algorithms: empirical results[J]. Evolutionary Computation , 2000, 8 (2) : 173-195 DOI:10.1162/106365600568202 |
| [66] | ABBASS H A, SARKER R, NEWTON C. PDE: a Pareto-frontier differential evolution approach for multi-objective optimization problems[C]//Proceedings of the 2001 Congress on Evolutionary Computation. Seoul, South Korea, 2011: 971-978. |
| [67] | GONG W, CAI Z. A multiobjective differential evolution algorithm for constrained optimization[C]//IEEE Congress on Evolutionary Computation. Hong Kong, China, 2008: 181-188. |
| [68] | QIAN W, YANG J, YANG Y, et al. A new random group search algorithm for solving the multi-objective programming problems[J]. Journal Liaoning Normal University , 2007, 30 (2) : 141 |
| [69] | NARA K, SHIOSE A, KITAGAWA M, et al. Implementation of genetic algorithm for distribution systems loss minimum re-configuration[J]. IEEE Transactions on Power Systems , 1992, 7 (3) : 1044-1051 DOI:10.1109/59.207317 |
| [70] | ZHU J Z. Optimal reconfiguration of electrical distribution network using the refined genetic algorithm[J]. Electric Power Systems Research , 2002, 62 (1) : 37-42 DOI:10.1016/S0378-7796(02)00041-X |
| [71] | ZHANG D, FU Z, ZHANG L. An improved TS algorithm for loss-minimum reconfiguration in large-scale distribution systems[J]. Electric Power Systems Research , 2007, 77 (5) : 685-694 |
| [72] | SRINIVASA R R, NARASIMHAM S V L, RAMALINGA R M. Optimal network reconfiguration of large-scale distribution system using harmony search algorithm[J]. IEEE Transactions on Power Systems , 2011, 26 (3) : 1080-1088 DOI:10.1109/IDAMS.2010.2076839 |



