证券投资是证券市场运行环节中的重要组成部分,而证券组合理论又是最重要的证券投资理论之一,著名学者Markowitz建立了求解最佳证券投资组合的解析模型。由于最佳证券组合的求解实际上属于一类组合优化问题,通常归结为二次规划模型[1-2],是一类典型的带约束NP-hard问题。可运用运筹学中的非线性规划法求解这类问题,但其求解过程往往十分复杂,而且对求解者的数学理论基础有较高要求[3-4]。
为了避免繁琐的数学规划求解,已有许多学者应用智能算法求解证券组合优化问题。张伟等[1]应用二进制编码遗传算法(genetic algorithm,GA)求解该问题,具有简洁、直观的优势,但效率不够高; 何洋林等[2]应用整数编码自适应遗传算法(adaptive GA,AGA)求解该问题,提高了求解效率; Soleimani等[3]应用GA求解含最大、最小交易量约束的投资组合优化模型; 夏梦雨等[4]则应用粒子群算法(particle swarm optimization,PSO)求解该问题; 刘晓峰等[5]应用PSO求解允许卖空证券投资和不允许卖空证券投资2种情形下的优化模型; 刘衍民等[6]应用具有约束处理机制的PSO求解自融资投资组合优化模型; 李磊等[7]应用2种版本的文化算法(cultural algorithm,CA)求解此模型; 江家宝等[8]以最大化个人经济效益或最大化周期结束时个人财富为目标,建立多阶段投资组合优化模型,再应用差分进化算法(differential evolution,DE)求解该问题。最近,有学者应用混合智能算法求解这类问题。李国成等[9]提出基于混沌搜索、PSO和引力搜索算法的混合元启发式搜索算法,并应用该算法求解基数约束投资组合问题;Lwin等[10]提出融合种群增量学习和DE的混合算法,再应用此方法求解约束投资组合模型。近年来,还有学者应用多目标进化算法(multiobjective evolutionary algorithm,MOEA)[11]求解投资组合优化问题。比如,Branke等[12]应用基于包络的MOEA求解组合投资问题的Pareto最优解。
由于人工蜂群算法(artificial bee colony algorithm,ABC)[13-15]具有良好的寻优性能,近年来受到广泛关注,故本文探索应用ABC算法求解证券组合优化问题。在引入约束优化问题可行性规则的基础上,提出面向证券组合优化问题的可行性规则人工蜂群算法(ABC algorithm with the feasibility rule,FRABC)。文中分析了FRABC算法的计算复杂度和全局收敛性。最后,给出数值实例,通过分析可知:FRABC算法的全局最优解好于AGA。同时,还与GA、PSO算法和基本ABC算法(basic ABC algorithm,BABC)进行对比实验,测试结果表明,FRABC算法具有良好稳健性,且性能指标优于4种对比算法。
1 投资组合优化数学模型文献[3]提出了基于我国证券市场现状的含交易费用的改进资产分配优化模型,简要描述如下。
设投资者可购买的证券集合为{s1,s2,…,sn},其中n为证券种数;证券si(i=1,2,…,n)的收益率为ri(随机变量),其期望收益率为Ri=E(ri),σij=cov(ri,rj)为随机变量ri和rj的协方差(i,j=1,2,…,n)。若允许的最小和最大投资金额分别为C1和C2,则投资金额C∈[C1,C2]。证券通常是以最小交易量“手”为基本单位买入和卖出的,设1手=Z股(Z∈Z+)。若证券si的现时报价为pi元/股,交易量为xi手(xi∈N),其投资组合向量为x=[x1 x2 … xn]T,则总投资金额为
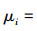

通常假设交易费用函数是投资金额的固定比例函数,即总交易费用为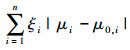

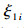
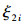

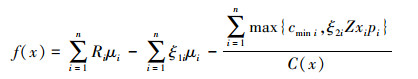 |
(1) |
投资组合x的风险为
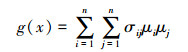 |
(2) |
投资者期望收益率高且风险小,因此,计入交易费用的加权优化模型为
 |
(3) |
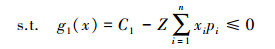 |
(4) |
 |
(5) |
式中:xi为整数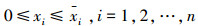
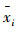
对于最大化问题式(3),具有总投资金额区间约束条件式(4)和式(5),属于约束优化问题,其求解难点在于如何处理约束条件[6]。本文采用可行性规则处理该约束条件,首先引入比较2个候选解的可行性规则[16]:
规则1 若2个候选解都是可行解,则目标函数值大的获胜。
规则2 若2个候选解都是不可行解,则约束违反度小的获胜。
规则3 若一个是可行解而另一个是不可行解,则可行解获胜。
在规则2中,需要应用候选解的约束违反度比较2个不可行解。本文将候选解x的约束违反度定义为
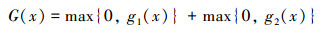 |
(6) |
显然,当x为可行解时,有G(x)=0。
2.2 可行性规则人工蜂群算法在Karaboga与Basturk[13-14]提出的ABC算法中,蜂群分为引领蜂群体、跟随蜂群体和侦察蜂群体,且依靠3种群体之间的交流、转换和协作来实现采蜜。同时,模型中应用蜜源来代表候选解,蜜蜂采蜜的过程即为搜寻最优解的过程。有关概念见文献[13-15],文中不赘述。
设蜂群规模为N,其中引领蜂和跟随蜂群体规模分别为NL和NF(通常取相同规模,即NL=NF=N/2)。因式(3)系非负整数规划问题,故在搜索过程中还需对决策变量取整。FRABC算法的流程如下:
1)初始化种群。按式(7)随机生成NL个候选解,并置采蜜时刻t=0。
 |
(7) |
式中:rand()为(0,1)内服从均匀分布的随机数,round(·)为四舍五入取整函数。
将在蜜源xk的邻域内未发现更优新蜜源的连续搜索次数记为δtk,初始时置δtk=0。
2)引领蜂采蜜。采蜜至第t时刻,每只引领蜂均在其当前蜜源的邻域内搜索,按式(8)生成新蜜源:
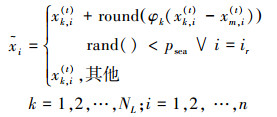 |
(8) |
式中: 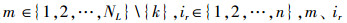
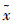
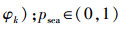


通过计算目标函数值


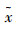



对NL只引领蜂(k=1,2,…,NL),执行NL次上述邻域搜索。
3)跟随蜂采蜜。跟随蜂的邻域搜索与蜜源更新方式与引领蜂一致。采蜜至第t时刻,每只跟随蜂均应用轮赌法选择被跟随的引领蜂。第k只引领蜂x(t+1)k被选中的概率为
 |
(9) |
式中:Fmax(t+1)、Fmin(t+1)为t时刻引领蜂群体中所有可行个体的最大、最小目标函数值;Gmax(t+1)、Gmin(t+1)为t时刻新一代引领蜂群体中所有不可行个体的最大、最小约束违反度。分母中加小正数可防止分母为0,从而避免程序中断。按式(9)设计选择概率,可行解被选中的概率区间为[0.2,1],而不可行解被选中的概率区间为[0.1,0.3]。使得可行解被选中的机会较大,而不可行解被选中的机会较小,但候选解(引领蜂群体)均有机会被选中,这样有利于引导跟随蜂搜索可行域及其边界,从而提高找到全局最优解的概率。
对NF只跟随蜂(k=1,2,…,NF),执行NF次上述邻域搜索。
4)侦察蜂采蜜。当δtk达到预设阈值Δt时,该蜜源对应的引领蜂转变为侦察蜂,应用式(7)重新随机产生新蜜源,并置δtk=0。
引领蜂转变为侦察蜂可增强种群的多样性,防止蜂群陷入局部最优区域。该操作可改善蜂群的搜索性能,提高获得最优解的概率。
5)更新最优蜜源。应用可行性规则确定新一代蜂群中的最优蜜源x(t+1)best。
6)终止判断。若满足终止条件,则输出最优蜜源x(t+1)best及其相应目标函数值F(x(t+1)best);否则,置t=t+1,返回2)。
2.3 计算复杂度分析设引领蜂群体规模NL和跟随蜂群体规模NF相同,且NL=NF=N/2,最大迭代代数为tmax。根据第3.2节中各步骤分析FRABC算法的计算复杂度(仅考虑重复执行的次数)。
2)的计算复杂度为:引领蜂执行邻域搜索生成新蜜源:O(N×n/2),评价新蜜源:O(N/2),更新蜜源:O(N/2),更新计数器δtk:O(N/2)。3)的计算复杂度为:计算引领蜂被选择的概率:O(N/2),选择被跟随的引领蜂:O(N/2),跟随蜂执行邻域搜索生成新蜜源:O(N×n/2),评价新蜜源:O(N/2),更新蜜源:O(N/2),更新计数器δtk:O(N/2)。5)的计算复杂度为:O(N/2),因此步存在不确定性,可忽略其复杂度5)的计算复杂度为:确定每代的最优蜜源:O(N/2),更新最优蜜源:O(1)。略去上述各步中的低阶项,则FRABC算法的计算复杂度为O(tmax×N×n),为立方阶复杂度[17]。
3 算法收敛性分析设问题式(3)的解空间为

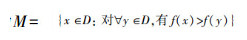
定义1 称t时刻的蜜源集合X(t)={x(t)k,k=1,2,…NL}为FRABC算法的第t代种群,t=0,1,…tmax。
定义2 称种群集合B={X={xk,k=1,2,…,NL}: X ∩M≠∅}为问题式(3)的满意种群集[18]。
由第2.2节的算法流程可知,FRABC算法具有保留精英解的特点,故有以下定理。
定理1 FRABC算法的最优蜜源x(t+1)best不劣于x(t)best,t=0,1,…,tmax。
定理2 FRABC算法的种群序列{X(t),t=0,1,…,tmax}是齐次不可约非周期Markov链。
证明 因蜂群对种群X(t)执行邻域搜索,生成新一代种群X(t+1)时,每一蜜源x(t+1)由引领蜂、跟随蜂及侦察蜂协同完成搜索[19]。借鉴车林仙[20]分析DE算法收敛性的方法,以下分别给出其一步转移概率(因篇幅所限,不再展开证明)。
1)引领蜂执行邻域搜索的一步转移概率。
引领蜂k在X(t)中随机选择一异于x(t)k的蜜源x(t)m,生成中间蜜源y的概率为
 |
(10) |
式中:Ts1为算子符号,以下类似;δ(·)为Dirac函数[20]。
对x(t)k与y执行交叉操作,生成
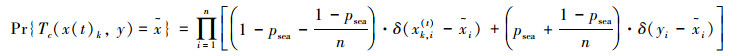 |
(11) |
对x(t)k与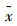
 |
(12) |
综合式(10)~(12),可得引领蜂k搜索到新蜜源x’的一步转移概率
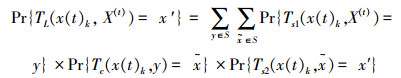 |
(13) |
2)跟随蜂执行领域搜索的一步转移概率。
当选中引领蜂k作为被跟随时,也可用前述方法计算搜索x’的一步转移概率,其表达式与式(13)类似,简记为
3)侦察蜂执行随机搜索的一步转移概率。
因侦察蜂对解空间S执行随机搜索,故获得x’的一步转移概率为
 |
式中:|S|表示S内的离散点数。
于是,仅由引领蜂搜出新一代蜜源x(t+1)k时,其概率为
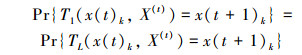 |
(14) |
由引领蜂和跟随蜂共同搜出新一代蜜源x(t+1)k时,其概率为
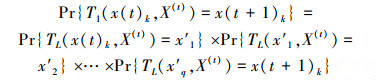 |
(15) |
式中:q≥1,指引领蜂k被跟随的次数。
由侦察蜂搜出新一代蜜源x(t+1)k时,其概率为
 |
(16) |
那么,由X(t)生成X(t+1)的一步转移概率为[19-20]
 |
(17) |
由式(14)~(17)可知,对∀X(t),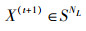
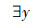
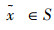
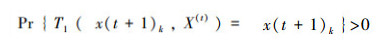
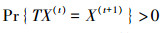
定理3 FRABC算法的Markov种群序列{X(t),t=0,1,…}以概率1收敛于问题式(3)的满意种群,即
证明 假设问题式(3)有惟一最优解。对∀X1,X2∈SNL,由定理1、2可得如下性质:
1)当X1∈B,X2∈B时,Pr{TX1=X2}>0,Pr{TX2=X1}>0,即X1和X2可互通;
2)当X1∈B,X2∉B时,Pr{TX1=X2}=0,Pr{TX2=X1}>0,即X1不能通向X2。
于是,B为正常返非周期不可约闭集[21],且有
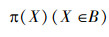
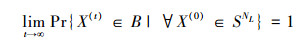 |
算例来自文献[2]。假设购买股票1手=100股(即Z=100),总投资金额上限C2=10万元,(C2-C1)/C2=0.2%。拟投资的n(=5)支股票的价格为p=[3.783.723.272.822.10]T (元/股)每支股票的投资金额最多占总金额的60%,进而可确定购买手数上限
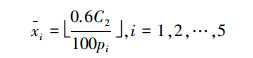 |
式中: 
每支股票的交易手续费比例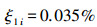
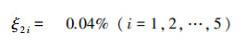
R=[0.01675 0.00859 0.05146 0.04227 0.09462]T
5支股票的风险方差方阵为
 |
根据第2.2节的FRABC算法流程,应用MATLAB编写程序,控制参数设置为:蜂群规模N=40,搜索概率psea=0.85,最大迭代代数tmax=600,代数阈值Δt=100。对于不同的风险偏好因子w,对应优化结果见表 1(分别独立运行50次,表中为最好结果)。FRABC算法独立运行一次的函数评价次数为N×tmax=24 000;而文献[2]的参数为N=20,tmax=200,AGA独立运行一次的函数评价次数为N×tmax=4 000。由表 1可知,对于不同的w,应用FRABC算法求出的加权优化结果F(x)均明显优于AGA。因此,虽然FRABC算法的函数评价次数高于AGA,但从优化结果来看,本文认为FRABC算法增加的计算开销是值得的。
| 风险偏好 因子w |
算法 | 股票交易量x/手 | 总投资 金额C/元 |
总收益率 f/% |
风险率g/% | 加权值F/% | |||||
| x1 | x2 | x3 | x4 | x5 | |||||||
| 0.0 | AGA | 119 | 81 | 2 | 67 | 25 | 99 912 | 2.260 8 | 0.609 1 | -0.609 1 | |
| FRABC | 36 | 162 | 0 | 92 | 0 | 99 816 | 1.766 1 | 0.254 6 | -0.254 6 | ||
| 0.1 | AGA | 22 | 114 | 63 | 51 | 68 | 99 987 | 3.441 6 | 1.068 7 | -0.617 6 | |
| FRABC | 30 | 162 | 0 | 100 | 0 | 99 804 | 1.822 9 | 0.259 1 | -0.050 9 | ||
| 0.2 | AGA | 16 | 99 | 100 | 35 | 69 | 99 936 | 3.807 5 | 1.307 6 | -0.284 6 | |
| FRABC | 0 | 162 | 39 | 95 | 0 | 99 807 | 2.235 8 | 0.341 5 | 0.174 0 | ||
| 0.3 | AGA | 17 | 76 | 125 | 32 | 73 | 99 927 | 4.205 2 | 1.671 8 | 0.091 3 | |
| FRABC | 0 | 136 | 82 | 80 | 0 | 99 966 | 2.694 0 | 0.506 4 | 0.453 7 | ||
| 0.4 | AGA | 4 | 81 | 131 | 30 | 81 | 99 951 | 4.371 8 | 1.791 7 | 0.673 7 | |
| FRABC | 0 | 91 | 153 | 57 | 0 | 99 957 | 3.471 4 | 0.933 0 | 0.828 7 | ||
| 0.5 | AGA | 15 | 70 | 131 | 28 | 83 | 99 873 | 4.427 2 | 1.904 2 | 1.261 5 | |
| FRABC | 0 | 67 | 184 | 21 | 42 | 99 834 | 4.323 4 | 1.628 6 | 1.347 4 | ||
| 0.6 | AGA | 14 | 39 | 194 | 15 | 59 | 99 858 | 4.745 3 | 2.160 5 | 1.983 0 | |
| FRABC | 0 | 46 | 184 | 0 | 108 | 99 960 | 5.313 2 | 2.843 4 | 2.050 6 | ||
| 0.7 | AGA | 9 | 42 | 185 | 8 | 86 | 99 837 | 5.025 3 | 2.508 7 | 2.765 1 | |
| FRABC | 0 | 0 | 184 | 0 | 189 | 99 858 | 6.786 5 | 5.630 7 | 3.061 3 | ||
| 0.8 | AGA | 4 | 33 | 117 | 9 | 216 | 99 945 | 6.408 9 | 5.308 3 | 4.065 5 | |
| FRABC | 0 | 0 | 122 | 0 | 286 | 99 954 | 7.664 4 | 8.388 6 | 4.453 8 | ||
| 0.9 | AGA | 5 | 10 | 109 | 35 | 232 | 99 843 | 6.841 9 | 6.583 9 | 5.499 4 | |
| FRABC | 0 | 0 | 122 | 0 | 286 | 99 954 | 7.664 4 | 8.388 6 | 6.059 1 | ||
| 1.0 | AGA | 2 | 20 | 70 | 33 | 283 | 99 822 | 7.191 1 | 7.831 1 | 7.191 1 | |
| FRABC | 0 | 0 | 122 | 0 | 286 | 99 954 | 7.664 4 | 8.388 6 | 7.664 4 | ||
| 注:表中AGA的计算结果引自文献[2] | |||||||||||
为了考察FRABC算法的有效性,本文还比较GA、PSO、BABC算法[13-14]和FRABC算法求解投资组合优化问题的优化性能。将可行性规则与GA、PSO和BABC算法结合形成的算法记为FRGA、FRPSO和FRBABC。
为了公平比较,所有算法的种群规模N、最大迭代代数tmax一致,取N=40,tmax=600,即函数评价次数一致。与FRABC算法类似,FRGA、FRPSO和FRBABC算法均采用非负整数编码,应用函数round(·)取整。FRGA应用概率选择(按式(9)选择,记为FRGA1)或2元锦标赛选择(记为FRGA2)、随机算术交叉[2]和均匀变异策略,交叉、变异概率分别为pc=0.9,pm=0.2。FRPSO算法的惯性权重ω线性递减,取ω=1.2~0.2,加速度系数为c1=c2=2,最大速度取
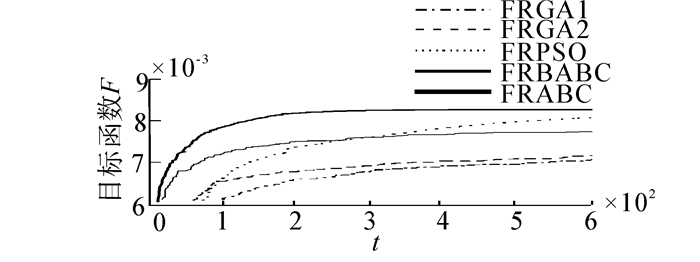
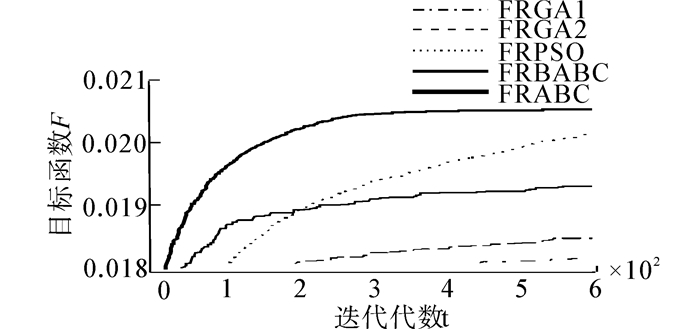
当w为0.4,0.5,0.6时,5种算法分别独立运行50次,平均最优目标函数值进化曲线如图 1~3所示,优化性能指标见表 2。其中,Fb、 Fw和Fav分别表示最好、最差和平均最优目标函数值,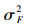
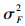
|
| 图 1 5种算法的平均进化曲线(w=0.4) Fig. 1 The average evolution curve of five algorithms(w=0.4) |

|
| 图 2 5种算法的平均进化曲线(w=0.5) Fig. 2 The average evolution curve of five algorithms(w=0.5) |
|
| 图 3 5种算法的平均进化曲线(w=0.6) Fig. 3 The average evolution curve of five algorithms(w=0.6) |
| 风险偏好 因子w |
算法 | 最好值Fb | 最差值Fw | 平均值Fav | 标准方差σF2 |
| 0.4 | FRGA1 | 7.939×10-3 | 6.147×10-3 | 7.098×10-3 | 3.427×10-4 |
| FRGA2 | 8.009×10-3 | 6.699×10-3 | 7.176×10-3 | 2.672×10-4 | |
| FRPSO | 8.287×10-3 | 6.962×10-3 | 8.096×10-3 | 2.715×10-4 | |
| FRBABC | 8.087×10-3 | 7.263×10-3 | 7.761×10-3 | 2.178×10-4 | |
| FRABC | 8.287×10-3 | 8.270×10-3 | 8.283×10-3 | 6.931×10-6 | |
| 0.5 | FRGA1 | 1.304×10-2 | 1.131×10-2 | 1.208×10-2 | 3.995×10-4 |
| FRGA2 | 1.271×10-2 | 1.153×10-2 | 1.209×10-2 | 2.849×10-4 | |
| FRPSO | 1.347×10-2 | 1.192×10-2 | 1.325×10-2 | 2.776×10-4 | |
| FRBABC | 1.324×10-2 | 1.219×10-2 | 1.271×10-2 | 2.623×10-4 | |
| FRABC | 1.347×10-2 | 1.345×10-2 | 1.347×10-2 | 4.575×10-6 | |
| 0.6 | FRGA1 | 1.923×10-2 | 1.718×10-2 | 1.820×10-2 | 4.555×10-4 |
| FRGA2 | 2.011×10-2 | 1.785×10-2 | 1.851×10-2 | 4.195×10-4 | |
| FRPSO | 2.050×10-2 | 1.833×10-2 | 2.012×10-2 | 4.318×10-4 | |
| FRBABC | 2.013×10-2 | 1.841×10-2 | 1.932×10-2 | 3.605×10-4 | |
| FRABC | 2.051×10-2 | 2.031×10-2 | 2.049×10-2 | 3.462×10-5 | |
5 结论
1)给出包含交易费用基于投资者风险偏好的最佳证券投资组合模型;针对其约束条件,定义了约束违反度函数,进而引入求解约束优化问题的可行性规则。
2)新型智能算法ABC在求解非线性优化问题中具有很强的全局寻优能力和很好的实用性,本文应用ABC算法求解最佳证券投资组合模型,形成面向该类问题的FRABC算法。
3) FRABC算法的计算复杂度为立方阶复杂度,与基本算法FRBABC一致。还应用Markov链分析其种群状态的一步转移概率,证明了该算法的全局收敛性。
4)应用MATLAB编写FRABC算法的计算程序,通过实例验证了该算法具有很强的寻优性能和良好的稳健性,且结果优于AGA。在相同函数评价次数的条件下,FRABC算法的各项优化指标均好于FRGA、FRPSO和FRBABC等对比算法,表明了本文方法的有效性和实用性。
| [1] | 张伟, 周群, 孙德宝. 遗传算法求解最佳证券组合[J]. 数量经济技术经济研究 , 2001 (10) : 114-116 ZHANG Wei, ZHOU Qun, SUN Debao. Genetic algorithm for portfolio investment optimizations[J]. Quantitative and Technical Economics , 2001 (10) : 114-116 |
| [2] | 何洋林, 叶春明, 徐济东. 基于改进AGA算法求解含交易费用组合投资模型[J]. 计算机工程与应用 , 2007, 43 (11) : 235-237 HE Yanglin, YE Chunming, XU Jidong. Portfolio investment model including transaction fee and solution based on adaptive genetic algorithm[J]. Computer Engineering and Applications , 2007, 43 (11) : 235-237 |
| [3] | SOLEIMANI H, GOLMAKANI H R, SALIMI M H. Markowitz-based portfolio selection with minimum transaction lots,cardinality constraints and regarding sector capitalization using genetic algorithm[J]. Expert Systems with Applications , 2009, 36 (3) : 5058-5063 DOI:10.1016/j.eswa.2008.06.007 |
| [4] | 夏梦雨, 叶春明, 徐济东. 用微粒群算法求解含交易费用的组合投资模型[J]. 上海理工大学学报 , 2008, 30 (4) : 379-381,386 XIA Mengyu, YE Chunming, XU Jidong. Solution of portfolio investment model including transaction fee with particle swarm algorithm[J]. Journal of University of Shanghai for Science and Technology , 2008, 30 (4) : 379-381,386 |
| [5] | 刘晓峰, 陈通, 张连营. 基于微粒群算法的最佳证券投资组合研究[J]. 系统管理学报 , 2008, 17 (2) : 221-224,234 LIU Xiaofeng, CHEN Tong, ZHANG Lianying. Study on the portfolio problem based on particle swarm optimization[J]. Journal of Systems and Management , 2008, 17 (2) : 221-224,234 |
| [6] | 刘衍民, 赵庆祯, 牛奔. 约束粒子群算法求解自融资投资组合模型研究[J]. 数学的实践与认识 , 2011, 41 (2) : 78-84 LIU Yanmin, ZHAO Qingzhen, NIU Ben. Constrain particle swarm optimizer for solving self-financing portfolio model[J]. Mathematics in Practice and Theory , 2011, 41 (2) : 78-84 |
| [7] | 李磊, 程晨, 张颖. 基于文化算法的投资组合规划问题求解[J]. 江南大学学报:自然科学版 , 2009, 8 (1) : 108-111 LI Lei, CHENG Chen, ZHANG Ying. Solving portfolio programming problem based on cultural algorithm[J]. Journal of Jiangnan University: Natural Science Edition , 2009, 8 (1) : 108-111 |
| [8] | 江家宝, 尤振燕, 孙俊. 基于微分进化算法的多阶段投资组合优化[J]. 计算机工程与应用 , 2007, 43 (3) : 189-193 JIANG Jiabao, YOU Zhenyan, SUN Jun. Multi-stage portfolio optimization using differentiation evolution algorithms[J]. Computer Engineering and Applications , 2007, 43 (3) : 189-193 |
| [9] | 李国成, 肖庆宪. 基数约束投资组合问题的一种混合元启发式算法求解[J]. 计算机应用研究 , 2013, 30 (8) : 2292-2297 LI Guocheng, XIAO Qingxian. Hybrid meta-heuristic algorithm for solving cardinality constrained portfolio optimization[J]. Application Research of Computers , 2013, 30 (8) : 2292-2297 |
| [10] | LWIN K, QU R. A hybrid algorithm for constrained portfolio selection problems[J]. Applied Intelligence , 2013, 39 (2) : 251-266 DOI:10.1007/s10489-012-0411-7 |
| [11] | PONSICH A, JAIMES A L, COELLO C A. A survey on multiobjective evolutionary algorithms for the solution of the portfolio optimization problem and other finance and economics applications[J]. IEEE Transactions on Evolutionary Computation , 2013, 17 (3) : 321-344 DOI:10.1109/TEVC.2012.2196800 |
| [12] | BRANKE J, SCHECKENBACH B, STEIN M, et al. Portfolio optimization with an envelope-based multi-objective evolutionary optimization[J]. European Journal on Operations Research , 2009, 199 (3) : 684-693 DOI:10.1016/j.ejor.2008.01.054 |
| [13] | KARABOGA D, BASTURK B. A powerful and efficient algorithm for numerical function optimization: artificial bee colony (ABC) algorithm[J]. Journal of Global Optimization , 2007, 39 (3) : 459-471 DOI:10.1007/s10898-007-9149-x |
| [14] | KARABOGA D, BASTURK B. On the performance of artificial bee colony (ABC) algorithm[J]. Applied Soft Computing , 2008, 8 (1) : 687-697 DOI:10.1016/j.asoc.2007.05.007 |
| [15] | 段海滨, 张祥银, 徐春芳. 仿生智能计算[M]. 北京: 科学出版社, 2011 : 88 -106. DUAN Haibin, ZHANG Xiangyin, XU Chunfang. Bio-inspired Computing[M]. Beijing: Science Press, 2011 : 88 -106. |
| [16] | MALLIPEDDI R, SUGANTHAN P N. Ensemble of constraint handling techniques[J]. IEEE Transactions on Evolutionary Computation , 2010, 14 (4) : 561-579 DOI:10.1109/TEVC.2009.2033582 |
| [17] | 温涛, 盛国军, 郭权, 等. 基于改进粒子群算法的Web服务组合[J]. 计算机学报 , 2013, 36 (5) : 1031-1046 WEN Tao, SHENG Guojun, GUO Quan, et al. Web service composition based on modified particle swarm optimization[J]. Chinese Journal of Computers , 2013, 36 (5) : 1031-1046 |
| [18] | 张文修, 梁怡. 遗传算法的数学基础[M]. 2版 西安: 西安交通大学出版社, 2003 : 118 -122. |
| [19] | 宁爱平, 张雪英. 人工蜂群算法的收敛性分析[J]. 控制与决策 , 2013, 28 (9) : 1554-1558 NING Aiping, ZHANG Xueying. Convergence analysis of artificial bee colony algorithm[J]. Control and Decision , 2013, 28 (9) : 1554-1558 |
| [20] | 车林仙.面向机构分析与设计的差分进化算法研究[D].徐州:中国矿业大学,2012: 21-30. CHE Linxian. Study on differential evolution algorithms orientating analysis and design of mechanisms[D]. Xuzhou: China University of Mining and Technology,2012: 21-30. |
| [21] | ZHANG Xiangyin, DUAN Haibin, YU Yaxiang. Receding horizon control for multi-UAVs close formation control based on differential evolution[J]. Science China Information Sciences , 2010, 53 (2) : 223-235 DOI:10.1007/s11432-010-0036-6 |



