多智能体的运动一致性在本质上与复杂网络的同步问题非常相似,都是要使网络中各个智能体的状态趋于一个一致的解,除了网络本身的性质对一致性的影响以外,各智能体之间的协调对于改善同步能力也是非常重要的[1]。近年来,结合网络一致性的多智能体群集控制一直是控制学者关注的问题,并且得到了许多重要的结论。如文献[2-5]讨论了一致性问题中系统网络拓扑结构的影响;文献[6-8]通过设计一个势能函数来实现多智能体的群集控制;文献[9]提出了同时考虑位移与速度协调的二阶一致性协议。另一方面,包含原理以及由其引申出的对对分解[10-13],可以充分地利用各子系统间的互联关系,在处理多重叠互联系统的协调控制时具有独特的优势。包含原理在运动体的协调控制方面有很广泛的应用,如自动车组系统[13-15]以及无人机编队[16]等的协调控制。由于前述文献中的系统运动模型是基于相对位置构建的,因而只适合于处理各运动体按链型结构排列的情况。本文将文献[13-14]中的系统扩展为2个轴向,考虑按网型结构排列的多智能体系统,为其建立一个多重叠的偏差状态方程,在包含原理的概念下分别为每一组在网络拓扑中相邻的智能体对设计一致性控制状态反馈矩阵,以收缩得到适用于原系统的协调控制器。系统网络拓扑的互联关系主要体现在一致性协调控制器中。
1 包含原理与系统描述 1.1 系统的置换包含原理系统的包含原理有扩展与收缩2个方面,可以有效地处理系统的重叠互联结构,从而简化复杂系统的分析与设计工作。通过对系统重叠的各个组成部分或子系统近似解耦,可以得到原系统在扩展空间中的对应,并且在满足包含原理相关的条件下,该扩展系统包含了原系统所有的性质。这样一来,可以在扩展空间中为每一个解耦的子系统进行并行且独立的观测器和控制器设计,经过适当的整合后,可以将得到的结果再收缩回原系统空间,进而实现对原系统的重叠分散与一致性协调控制。关于系统包含原理以及重叠互联系统协调控制方面的详细内容请见文献[10-13]。
考虑一线性定常连续的重叠互联系统,具有N(N ≥ 3)个子系统:
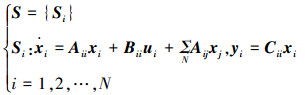 |
(1) |
式中:xi(t)∈Rni,ui(t)∈Rmi和yi(t)∈Rli分别是在时间t∈R子系统Si的状态、输入和输出向量;Aii、Bii和Cii是系统Si的系数矩阵,Aij表示子系统Si与子系统Sj的互联关系。
对于式(1),系统中所有的互联关系都是建立在每一对子系统间的信息结构约束之上的,因而可以在式(1)中任意选择系统S的一对子系统Si与Sj,称
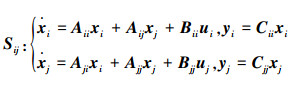 |
(2) |
为系统S的一个基本互联子系统对。在式(2)中,只需要关注特定子系统Si与Sj之间的互联关系,而这2个子系统与其他任意子系统间的互联关系可以暂时不做考虑,这样可以在很大程度上简化了复杂互联系统的分析工作,又不会损失细节。
重叠互联系统的对对分解需要考虑扩展空间中子系统对Sij的排列顺序,即循环逆序排列,假设系统S具有全网络结构,则有各子系统对按倒序下标循环排列为
 |
这种排列允许系统S中最后一个子系统SN直接脱离主体系统,或是子系统SN+1直接加入,而不会影响原有的排列顺序,可以用于处理系统间互联关系的变化。循环逆序排列是通过对系统S进行一系列对称置换得到的,在扩展空间中,假设一个具有块维数为 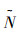
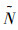
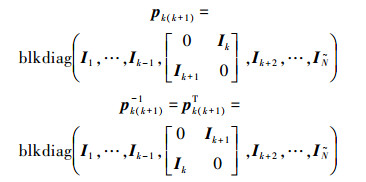 |
式中:Ik是对应子系统Sk的单位子矩阵。从而有列组置换矩阵P与行组置换矩阵P-1由一系列相邻列组与行组初等置换矩阵按顺序右累乘与左累乘得到
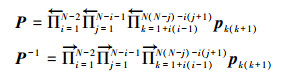 |
为将系统S扩展成各子系统对Sij按循环逆序排列的扩展系统 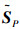
 |
(3) |
置换后可得
 |
分别满足包含条件UPVP=In,QPRP=Im以及SPTP=Il。据此可以给出扩展系统 
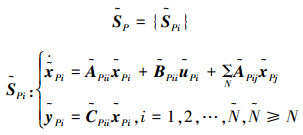 |
(4) |
其中各系数矩阵分别为
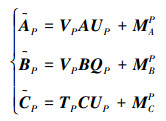 |
(5) |
式中:MAP、MBP和MCP分别是系统扩展后的补偿矩阵。文献[12-13]介绍了一组在对对分解意义下合适的补偿形式,限于篇幅这里不再赘述。
1.2 多智能体系统的偏差模型和重叠结构分解考虑用每个智能体位移的变化量和速度的变化量来描述其运动状态,可以写出每个智能体的二阶偏差方程为
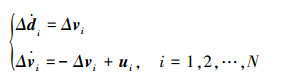 |
(6) |
为简便起见以下将省略变化量符号,式(6)中di=[dix diy]T,vi=[vix viy]T,ui=[uix uiy]T,分别表示智能体i在x和y轴上的位移与速度变化量以及控制输入。
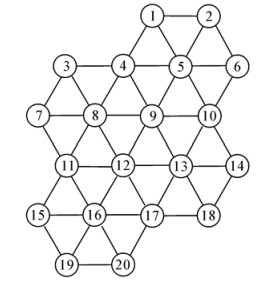
如图 1所示,考虑由N=20个智能体组成的网型结构系统。容易想象,对于这样的网型拓扑结构,当每一对智能体间的距离均相等时,一定会形成图中正三角形网格的网型结构,即是文献[8]中定义的α-lattice。不过,文献[8]的群集算法主要考虑智能体的势能关系,这样一来各智能体对相互距离的判断可能会产生误差,在实际形成的网型拓扑结构中各边的长度可能不会完全相等,即形成准α-lattice。本文在接下来要介绍的多智能体一致性协调控制将直接考虑各智能体位移和速度的变化量,因而在平稳状态下各智能体间的距离将是完全相等的。
|
| 图 1 多智能体系统网络拓扑结构, N=20 Fig. 1 Network topology of a multi-agent system, N=20 |
根据式(6)描述的系统动态建立状态空间模型。选取x=[d1v1d2v2…d20v20]T作为系统的状态变量,u=[u1 u2 … u20]T为各智能体的控制输入,y=[y1d y1v … y20d y20v]T=[d1 v1 … d20 v20]T作为系统的输出变量。这样就可以为系统建立一个具有重叠互联结构的动态模型,各智能体间的关联一方面体现在其状态矩阵本身的重叠上,另一方面则是系统的控制输入。
图 1表示的系统状态空间模型为
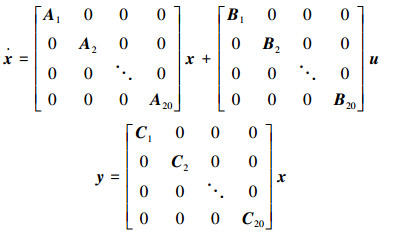 |
(7) |
式中:
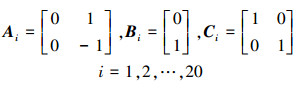 |

根据图 1所示的网络结构,扩展系统中各子系统对的循环逆序可以写成
 |
(8) |
这样,根据式(3)可以选择系统状态的扩展和收缩变换矩阵为
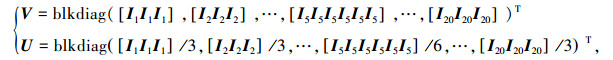 |
(9) |
系统输入、输出的扩展和收缩变换矩阵结构与式(9)类似。系统的置换矩阵若要按照定义式来选择稍显不够直观,这里可以参照文献[17]中的式(6),即
 |
式中:符号P(m,n)b表示P中单位子矩阵I的块位置。补偿矩阵的选择可以参照文献[12-13]。这样即可根据式(4)、(5)得到原多智能体系统的扩展系统。
2 多智能体的一致性协调控制考虑多智能体系统偏差模型(7),控制目标是要使各智能体的位移和速度变化量为0,且整体系统实现运动状态的一致。针对重叠解耦后的扩展系统,以其中的每个子系统对为基本单位,参照文献[9]中提出的二阶一致性协议,可以构造智能体对的一致性控制律为
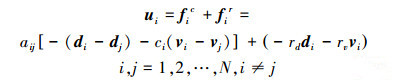 |
(10) |
式中:fic是为保证系统运动一致性的实现,fir是为保证各智能体的位移与速度变化量为0,各参数aij、ci、rd和rv取合适的值。从而可以把式(11)整理成状态反馈矩阵的形式:
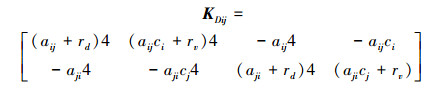 |
(11) |
即可得到扩展系统的状态反馈控制矩阵为
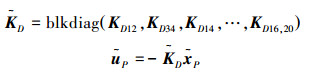 |
(12) |
需要注意的是,根据文献[12-13],在整合扩展系统控制矩阵时需要考虑整体系统的信息结构,即需要参照由包含原理得到的扩展系统状态矩阵的信息结构,对控制矩阵进行补偿。这里由于系统的状态矩阵中对应的信息结构约束项为0,从而相应的协调补偿器也为0。
然后需要根据包含原理相关条件将扩展系统的协调控制器(12)收缩回原空间,由文献[12-13]有
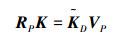 |
即此时原系统的协调控制矩阵K可以由扩展系统的控制矩阵 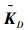
实际上,考虑基于包含原理得到的一致性控制律u=-Kx,其基本结构与常规的一致性协议如文献[4, 9]中提到的是相同的,差别仅在于每一路控制输入整体的系数上。这主要是因为常规的一致性协议使用系统网络的Laplacian矩阵来描述网络拓扑结构,而该矩阵在构造时是以网络中各节点的互联项作为基准单位,而本文的描述方式是以该节点本身作为基准单位,二者相差的系数恰好是节点所含的互联项的数目。
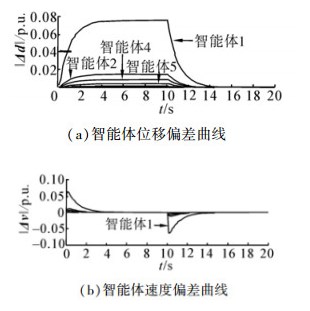
3 仿真示例首先考虑图 1所示的多智能体系统,各智能体仅能与存在信息结构约束的其他智能体进行信息交换,即是在一致性控制律(10)中,i与j需要满足Sij存在于子系统的循环逆序排列里。系统的重叠偏差模型如式(7),设智能体1在1≤t≤10 s内在x轴和y轴上均受到一个正单位的扰动,控制律中各参数在整个仿真过程中是固定的,分别为aij=10,ci=1,rd=rv=10,使用MATLAB仿真如图 2。
|
| 图 2 N=20时多智能体系统的响应曲线 Fig. 2 Response curves of the multi-agent system, N=20 |
图 2中 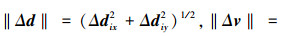


|
| 图 3 向系统中加入一个智能体,N=21 Fig. 3 Add one more agent to the former system, N=21 |
假设系统经调节后处于平稳运行状态,智能体21的加入将分别给智能体17、18和20一个正单位的扰动,智能体21本身受到一个负单位的扰动,控制律中各参数不变。仿真结果如图 4,这里各智能体所受扰动为瞬时值,因而速度变化量的调节时间很短。智能体17、18和20在系统网络中的地位和作用很接近,其位移与速度变化量的响应曲线也很相似,并且与智能体21的响应曲线变化方向相反,其他智能体的响应曲线波动依然是按照其各自的互联情况不同而有一定的差别,这与图 2显示的结果是基本一致的。以上仿真结果表明,在网络拓扑结构改变的情况下,系统仍然可以很快地调节回平衡位置。

|
| 图 4 N=21时多智能体系统的响应曲线 Fig. 4 Response curves of the multi-agent system, N=21 |
本文在包含原理的概念下考虑多智能体系统的运动一致性问题。通过对系统重叠偏差方程进行扩展、为每个智能体对单独设计控制律、再将结果整合并收缩这样的过程,可以实现原系统的一致性协调控制。区别于之前的工作,本文解决了在2个运动轴向上应用包含原理进行系统重叠分解的问题。文中各智能体间距离相等的网型结构是有现实意义的,在自动车组的队形保持或多机器人系统的群集控制中均有应用价值。另一方面,不只是本文提到的一致性问题,基于置换包含原理的对对分解也同样适用于处理更加复杂的控制算法以及网络结构的动态变化。
| [1] | 段志生, 黄琳. 几类协调控制问题及其应用[J]. 控制工程 , 2010, 17 (suppl) : 1-8 DUAN Zhisheng, HUANG Lin. Several harmonic control problems and their applications[J]. Control Engineering of China , 2010, 17 (suppl) : 1-8 |
| [2] | JUSTH E W, KRISHNAPRASAD P S. A simple control law for UAV formation flying, 2002-38[R]. Institute for System Research, University of Maryland, 2002. |
| [3] | JADBABIE A, LIN J, MORSE A S. Coordination of groups of mobile agents using nearest neighbor rules[J]. IEEE Transactions on Automatic Control , 2003, 48 (6) : 988-1001 DOI:10.1109/TAC.2003.812781 |
| [4] | OLFATI-SABER R, MURRAY R M. Consensus problems in networks of agents with switching topology and time-delays[J]. IEEE Transactions on Automatic Control , 2004, 49 (9) : 1520-1533 DOI:10.1109/TAC.2004.834113 |
| [5] | OLFATI-SABER R, FAX J A, MURRAY R M. Consensus and cooperation in networked multi-agent systems[J]. Proceedings of the IEEE , 2007, 95 (1) : 215-233 DOI:10.1109/JPROC.2006.887293 |
| [6] | TANNER H G. Flocking with obstacle avoidance in switching networks of interconnection vehicles[C]//IEEE International Conference on Robotics and Automation. [S.l.], 2004: 3006-3011. |
| [7] | TANNER H G, JADBABAIE A, GAPPAS G J. Flocking in fixed and switching networks[J]. IEEE Transactions on Automatic Control , 2007, 52 (5) : 863-868 DOI:10.1109/TAC.2007.895948 |
| [8] | OLFATI-SABER R. Flocking for multi-agent dynamic systems: algorithms and theory[J]. IEEE Transactions on Automatic Control , 2006, 51 (3) : 401-420 DOI:10.1109/TAC.2005.864190 |
| [9] | REN W, ATKINS E. Distributed multi-vehicle coordinated control via local information exchange[J]. International Journal of Robust and Nonlinear Control , 2007, 17 (10/11) : 1002-1033 |
| [10] | CHEN X B, STANKOVIC S S. Decomposition and decentralized control of systems with multi-overlapping structure[J]. Automatica , 2005, 41 : 1765-1772 DOI:10.1016/j.automatica.2005.01.020 |
| [11] | CHEN X B, STANKOVIC S S. Overlapping decentralized approach to automatic generation control of multi-area power systems[J]. International Journal of Control , 2007, 80 : 386-402 DOI:10.1080/00207170601001706 |
| [12] | CHEN X B, XU W B, HUANG T Y, et al. Pair-wise decomposition and coordinated control of complex systems[J]. Information Science , 2012, 185 : 78-99 DOI:10.1016/j.ins.2011.09.017 |
| [13] | 陈雪波. 系统包含原理及其应用[M]. 北京: 科学出版社, 2012 : 12 -17. |
| [14] | 陈雪波. 车组距离与速度偏差系统的建模与仿真[C]//第20届中国控制会议论文集. 大连, 中国, 2001: 553-558. CHEN Xuebo. Modeling and simulation for car-string velocity and distance bias systems[C]//Proceedings of the 20th China Control Conference. Dalian, China: 2001: 553-558. |
| [15] | STANKOVIC S S, STANJEVIC M J, SILJAK D D. Decentralized suboptimal LQG control of a platoon of vehicles[C]//The 7th Balkan Conference on Operational Research. Constanta, Romania, 2005: 12-15. |
| [16] | STIPANOVIC D M, INALHAN G, TEO R, et al. Decentralized overlapping control of a formation of unmanned aerial vehicles[J]. Automatica , 2004, 40 : 1285-1296 DOI:10.1016/j.automatica.2004.02.017 |
| [17] | CHEN X B, MA C. Coordinated control of a four-area power system under structural perturbation[C]//The 9th Asian Control Conference. Istanbul, Turkey, 2013:14-17. |
| [18] | 马晨, 陈雪波. 互联系统的动态信息结构约束[J]. 系统科学与数学 , 2013, 33 (11) : 1301-1320 MA Chen, CHEN Xuebo. Dynamic of interconnected system information structure constraints[J]. Journal of System Science and Mathematical Science , 2013, 33 (11) : 1301-1320 |



