2. 广西混杂计算与集成电路设计分析重点实验室,广西 南宁 530006
2. Guangxi Key Laboratory of Hybrid Computation and IC Design Analysis, Nanning 530006, China
视频目标跟踪是近年来计算机视觉领域中的研究热点,在人机交互、视频监控、智能交通等方面都有着广泛的应用。粒子滤波算法(particle filter,PF)因能有效地解决视频目标跟踪中普遍存在的非线性、非高斯性的问题[1],在视频跟踪领域得到了足够的重视[2-4]。而在实际应用中,粒子滤波却存在权值退化现象,虽然通过采用重采样技术可以复制大权值样本[5],但又不可避免地会导致粒子匮乏问题[6],当系统噪声较小时,易造成样本的聚集。为解决这一问题,提高粒子滤波的采样效率,一些学者提出选取更好的提议分布,采用复杂的抽样策略。比如辅助采样、分区采样、退火重要性采样等[7]。
拟蒙特卡洛(Quasi-Monte Carlo, QMC)方法是一种确定性的采样方法,它利用准随机数产生均匀分布在状态空间的点,与MC方法的随机样本分布不同,QMC方法能产生低偏差序列的样本,基于QMC方法的粒子滤波(Quasi-Monte Carlo particle filter, QMCPF)用更少的粒子就能达到所需的精度,能有效地解决基于MC的随机采样过程获得的粒子在状态空间积聚在一起或形成空隙的问题。
本文提出利用数论中的佳点集理论和方法[8]来构造一种新的拟蒙特卡洛序列。利用佳点集方法取的点要比随机取点的偏差更小,并且佳点集序列与常用的拟蒙特卡洛序列Halton序列相比分布更均匀,在滤波过程中可提高状态估计的精度和收敛速度,减少了样本重叠,避免了运算的浪费,提高了样本的质量。在非线性系统状态估计精度要优于粒子滤波和现有的拟蒙特卡洛粒子滤波算法。将GPS-QMCPF应用于视频目标跟踪中,实验结果表明,基于GPS-QMCPF的视频目标跟踪算法能较好地解决有遮挡情况下的跟踪,同时还能一定程度上缩减跟踪时间;实验还比较了PSO-PF和PSO优化GPS-QMCPF算法在视频目标跟踪中的性能数据,发现在PSO-PF算法中加入佳点集思想同样能起到增加粒子有效样本数和降低重采样次数的作用。
1 QMCPF算法 1.1 QMC方法QMC方法采用低差异序列生成样本,可有效地避免随机抽样中可能出现的样本空隙和样本聚焦现象[9]。目前已经提出的拟蒙特卡洛序列主要有Van der Corput序列、Faure序列、Sobol序列、Halton序列以及Niederreiter的(t, s)序列。
在实际应用中使用较多的是Halton序列,可以根据式(1)、(2)得到
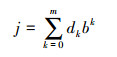 |
(1) |
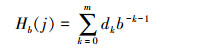 |
(2) |
式中:b为基数,m、dk分别为项数和系数。
1.2 QMCPF算法QMCPF算法关键是以QMC方法代替MC方法来实现粒子滤波的采样过程,QMC方法生成的低差异样本序列能使QMCPF的精度优于PF[9]。QMCPF的主要思路如下:先以QMC方法生成初始低差异粒子集,通过生成支撑区间来映射k时刻低差异性的粒子集;随后根据k-1时刻所有粒子的分布情况计算k时刻的权重。
2 基于佳点集拟蒙特卡洛的粒子滤波算法(GPS-QMCPF)利用数论中的佳点集理论和方法来设计一个新的生成低差异样本序列的QMC算法。因能构造出更均匀、更低偏差的点集。可提高拟蒙特卡洛的粒子滤波算法估计的准确度和加快算法的收敛速度。
2.1 佳点集理论佳点集的定义与构造[8]:
1)设Gt是S维空间中的单位立方体,即x∈Gt,x=(x1, x2, …, xt),其中0≤xi≤1(i=1, 2, …, t)。
2)设Gt中有一点集(n个点),pn(k)=x1(n)(k), …, xt(n)(k), 1≤k≤n, 其中0≤xi(n)(k)≤1(1≤i≤t)。
3)对任一给定Gt中的点〈r〉=(r1, r2, …,rt),令Nn(〈r〉)=Nn(r1, r2, …,rt)表示pn(k)中满足不等式(3)、(4)的点的个数:
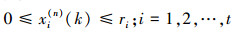 |
(3) |
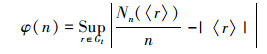 |
(4) |
式中:|〈r〉|=r1, r2, …,rt,则称点集pn(k)有偏差φ(n)。若对任一n,均有φ(n)=O(1),则称pn(k)在Gt上是一致分布的且偏差为φ(n)。
4)令〈r〉∈Gt,形成pn(k)=r1∗k, r2∗k, …, rt∗k (k=1, 2, …, n)的偏差φ(n)满足φ(n)=C(r, ε)n-1+ε,其中C(r, ε)是只与r, ε(ε>0)有关的常数,则称pn(k)为佳点集,〈r〉称为佳点。
5)取rk={2cos(2πk/p)}(1≤k≤t)或rk={exp(k)}(1≤k≤t),p是满足(p-s)/2≥s的最小素数,则〈r〉是佳点。
2.2 GPS-QMCPF算法的优点拟蒙特卡洛方法计算的准确性及收敛速度主要取决于偏差,偏差用来度量点列在函数域上的均匀分布程度,点列分布越均匀,偏差就越小,收敛速度就越快,波动也相应地会减小,计算准确度也随之提高。可以用Koksma-Hlawka不等式给出拟蒙特卡洛方法的计算误差如式(5)所示。
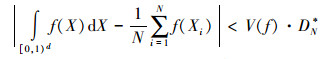 |
(5) |
式中:V(f)为Hardy and Krause意义下f的有界变差,DN*为点列{X1, X2,…, XN}的星偏差。随机数序列的偏差期望值可限制在(log(logN))N-1/2,而用佳点集序列代替随机序列可以提高精度,最小偏差可达O((logN)s-1N-1)[10]。
GPS-QMC方法的收敛速度是O(logdN/N)高于MC方法的收敛速度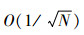
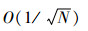
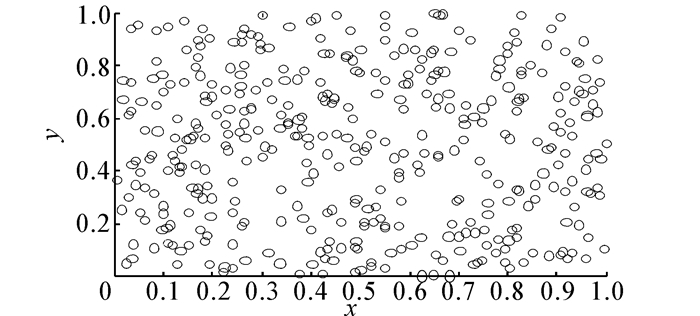
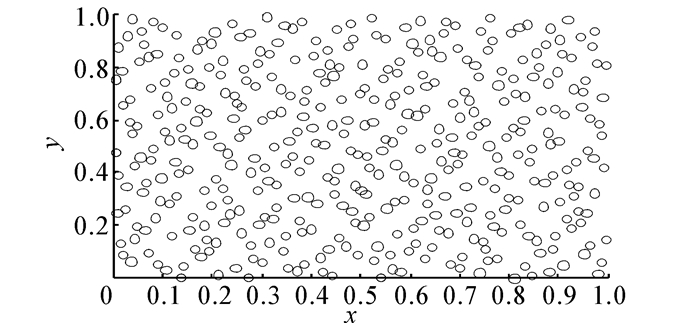
标准的拟蒙特卡洛粒子滤波算法一般采用Halton序列为初始采样序列。构造400个二维佳点集和400个二维Halton点集,同时用随机方法在二维空间内取400个点,图 1~3分别给出了它们的分布效果。可以看出,佳点集的分布要比Halton序列和随机序列更均匀。而且只要取点个数一定,每次所得的分布效果是一致的,由此可知佳点集稳定性较好。其次佳点集的构造与空间维数无关,能够很好地适应高维问题。
|
| 图 1 400个二维随机点集 Fig. 1 400 two-dimensional random point set |
|
| 图 2 400个二维Halton点集 Fig. 2 400 two-dimensional Halton sequence point set |

|
| 图 3 400个二维佳点集 Fig. 3 400 two-dimensional good point set |
GPS-QMCPF利用GPS-QMC方法的低偏差序列生成均匀分布的样本,改善了样本聚焦和样本空隙的现象,使得GPS-QMCPF的精度明显优于PF;并且通过图 2、3,可以看出GPS-QMC方法的低偏差序列比Halton序列更均匀,因为点列分布越均匀,偏差就越小,收敛速度也越快,因此GPS-QMCPF算法比标准的QMCPF算法的精度也要更好。
2.3 GPS-QMCPF的计算步骤1)初始化。在初始时刻从重要性函数中采样N个粒子{x0:k
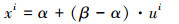 |
(6) |
2)估计xk的支撑区间[αk, βk],产生在区间[0, 1)d内的低差异性样本点集{uj, j=1, 2,…, N},利用式(6)将其映射到[αk, βk],形成在k时刻的样本粒子群{xkj, j=1, 2,…, N},利用式(7)计算预测密度值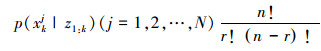
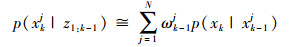 |
(7) |
3)利用式(8)计算粒子的权值:
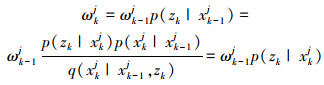 |
(8) |
4)将权重归一化:
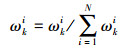 |
(9) |
5)状态值估计:
 |
(10) |
为了验证文中GPS-QMCPF法的有效性,程序基于MATLAB R2012a和VC++ 6.0编程环境在CPU为AMD Athlon(tm) II X2 B24 Processor 2.99 GHz,内存为1.75 GB的PC机上运行。
3.1 单变量非静态增长模型选取单变量非静态增长模型(UNGM模型),仿真对象的过程模型和观测模型如下。
过程模型:
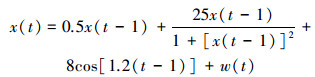 |
(11) |
观测模型:
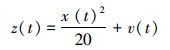 |
(12) |
式中:w(t)和v(t)为零均值高斯噪声。
采用PF,文献[11]中对QMCPF改进后的NQMCPF算法,文献[12]中的TR-SQMC,GPS-QMCPF估计该非线性系统的状态。实验取过程噪声方差Q为10、观测噪声方差R为1进行仿真,具体数据如表 1所示(RMSE为均方根误差)。
| 算法 | RMSE | 状态估计时间/ms | |||||
| N=500 | N=200 | N=100 | N=500 | N=200 | N=100 | ||
| PF | 4.177 | 6.045 | 9.214 | 9.86 | 6.27 | 5.20 | |
| NQMCPF | 1.885 | 2.985 | 4.319 | 9.81 | 5.90 | 5.10 | |
| TR-SQMC | 1.763 | 2.895 | 4.174 | 9.86 | 6.20 | 5.17 | |
| GPS-QMCPF | 1.597 | 2.654 | 4.091 | 9.76 | 5.56 | 5.06 | |
| 算法 | 平均有效样本数 |
| PF | 36.422 |
| NQMCPF | 59.151 |
| TR-SQMC | 62.448 |
| GPS-QMCPF | 64.617 |
由实验结果可以看出,基于GPS-QMC方法的粒子滤波可以用较少的粒子达到所需要的精度。PF的误差远高于QMC-PF、TR-SQMC和GPS-QMCPF,其中GPS-QMCPF的误差最小。并且GPS-QMCPF算法减少了样本的重叠和聚焦现象,减轻了粒子的退化程度,所以有效样本数大于PF、NQMCPF和TR-SQMC算法。
3.2 在视频目标跟踪中的应用 3.2.1 建立运动模型跟踪目标外轮廓通常采用椭圆或矩形,目标状态可以表示为
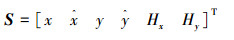 |
(13) |
式中:(x, y)表示椭圆或矩形的中心点坐标,Hx和Hy分别为矩形的半长轴或半宽轴(椭圆的长轴和短轴),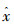

本文采用一阶常速模型描述跟踪目标的运动规律,在整个运动过程中,目标中心(x, y)采用常速运动模型,而(Hx, Hy)采用随机扰动模型,因此,建立运动方程[13]:
 |
(14) |
本文采用最常用的颜色直方图作为目标特征观测模型,采用巴特查理亚距离(Bhattacharyya)作为目标颜色直方图与粒子区域的颜色直方图相似性的量度。对于2个连续分布p(u)和q(u)的巴特查理亚系数为
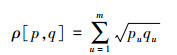 |
(15) |
巴特查理亚距离为[14]
 |
(16) |
当d值越小说明候选区域的颜色直方图与目标区域的颜色直方图越相似,应赋予较大的粒子权值,反之,则相似程度越低,粒子权值也越小。因此,观测似然函数可以表示为
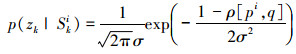 |
(17) |
粒子的权值为
 |
(18) |
为了验证算法的有效性,进行了大量视频目标跟踪的实验,分别对比PF、NQMCPF算法和GPS-QMCPF算法的跟踪效果。
在实验中,首先要在初始帧手动选取参考目标并计算目标区域的颜色直方图,并在选定目标区域中随机采样N个粒子,如图 4~5所示,在一组遥控玩具直升飞机的视频序列中的PF算法随机采样和GPS-QMCPF算法佳点集采样情况,取粒子数为100,从图中可以看出佳点集的分布均匀且集中。

|
| 图 4 初始帧目标区域随机采样 Fig. 4 Random sampling around the target in the first frame |

|
| 图 5 初始帧目标区域佳点集采样 Fig. 5 Good point set sampling around the target in the first frame |
如图 6~8所示。这组视频序列实验中,361-365帧直升机部分被遮挡。从实验效果图可以看出GPS-QMCPF算法跟踪效果比PF算法好,精度更高。

|
| 图 6 PF算法的跟踪效果 Fig. 6 PF algorithm tracking performance |

|
| 图 7 NQMCPF算法的跟踪效果 Fig. 7 NQMCPF algorithm tracking performance |

|
| 图 8 GPS-QMCPF算法的跟踪效果 Fig. 8 GPS-QMCPF algorithm tracking performance |
对这组视频序列实验中PF和GPS-QMCPF算法的计算量进行分析。取视频第81~480帧,统计20次实验数据的平均值。
表 3~4的数据表明,GPS-QMCPF算法可增加粒子的有效样本数,减少重采样次数,同时可降低计算量,运行时间相应也降低,跟踪的实时性得到了提高。
本文再将文献[15]提出的粒子群优化粒子滤波算法(particle swarm optimization particle filtering, PSO-PF)应用于视频目标跟踪中,并与粒子群优化的GPS-QMCPF算法进行对比,实验性能数据对比见表 5~6,实验取视频第81~480帧,统计20次实验数据的平均值。
| 算法 | 有效样本数 | 重采样次数 | 平均重采样率/% | ||||||||
| N=300 | N=200 | N=100 | N=300 | N=200 | N=100 | N=300 | N=200 | N=100 | |||
| PF | 179.400 | 118.345 | 58.811 | 203.7 | 203.7 | 214.0 | 50.9 | 52.4 | 53.5 | ||
| NQMCPF | 183.448 | 121.959 | 60.259 | 192.2 | 195.6 | 197.6 | 48.1 | 48.9 | 49.4 | ||
| GPS-QMCPF | 186.951 | 124.052 | 63.856 | 182.0 | 184.5 | 186.6 | 45.5 | 46.1 | 46.7 | ||
| 算法 | 运行时间/s | 每秒处理平均帧数 | |||||
| N=300 | N=200 | N=100 | N=300 | N=200 | N=100 | ||
| PF | 17.827 | 16.674 | 15.621 | 22.438 | 23.989 | 25.607 | |
| NQMCPF | 17.777 | 16.544 | 15.489 | 22.501 | 24.178 | 25.825 | |
| GPS-QMCPF | 17.221 | 16.045 | 15.006 | 23.227 | 24.930 | 26.656 | |
表 5~6的数据表明,在PSO-PF算法中加入佳点集思想进行初始采样在视频目标跟踪领域同样能增加粒子的有效样本数,减少重采样次数,加快算法收敛,进而降低算法的运行时间,提高跟踪的实时性。
| 算法 | 有效样本数 | 重采样次数 | 平均重采样率/% | ||||||||
| N=300 | N=200 | N=100 | N=300 | N=200 | N=100 | N=300 | N=200 | N=100 | |||
| PSO-PF | 198.306 | 130.010 | 65.479 | 145.6 | 147.8 | 148.2 | 36.4 | 37.0 | 37.1 | ||
| PSO优化GPS-QMCPF | 203.369 | 134.082 | 68.754 | 138.5 | 140.5 | 142.6 | 34.6 | 35.1 | 35.6 | ||
| 算法 | 运行时间/s | 每秒处理平均帧数 | |||||
| N=300 | N=200 | N=100 | N=300 | N=200 | N=100 | ||
| PSO-PF | 27.923 | 23.703 | 19.490 | 14.325 | 16.876 | 20.523 | |
| PSO优化GPS-QMCPF | 27.438 | 23.334 | 19.131 | 14.578 | 17.142 | 20.908 | |
4 结束语
本文提出的GPS-QMCPF算法,利用佳点集确定性采样代替了粒子滤波中的随机采样,使采样粒子分布更加均匀,减少了样本重叠,避免了运算的浪费,提高了样本的质量,同时加快了收敛速度,在非线性系统状态估计精度要优于粒子滤波和现有的拟蒙特卡洛粒子滤波算法。实验结果表明,基于GPS-QMCPF的视频目标跟踪算法能较好地解决有遮挡情况下的跟踪,同时还能一定程度上缩减跟踪时间;实验还比较了PSO-PF和PSO优化GPS-QMCPF算法在视频目标跟踪中的性能数据,发现在PSO-PF算法中加入佳点集思想同样起到增加粒子有效样本数和降低重采样次数的作用。
| [1] | 姚剑敏, 辛琦, 郭太良. 一种基于粒子滤波的自适应相关跟踪算法[J]. 武汉理工大学学报 , 2008, 30 (1) : 6-9 YAO Jianmin, XIN Qi, GUO Tailiang. Adaptive correlation tracking algorithm based on particle filter[J]. Journal of Wuhan University of Technology , 2008, 30 (1) : 6-9 |
| [2] | 朱明清, 王智灵, 陈宗海. 基于改进Bhattacharyya系数的粒子滤波视觉跟踪算法[J]. 控制与决策 , 2012, 27 (10) : 1579-1583 ZHU Mingqing, WANG Zhiling, GHEN Zonghai. Modified Bhattacharyya coefficient for particle filter visual tracking[J]. Control and Decision , 2012, 27 (10) : 1579-1583 |
| [3] | MADRIGAL F, RIVERA M, HAYET J B. Learning and regularizing motion models for enhancing particle filter-based target tracking[J]. Advances in Image and Video Technology Lecture Notes in Computer Science , 2012, 7088 : 287-298 |
| [4] | 王爱侠, 李晶皎, 王青, 等. 基于多核的并行粒子滤波运动目标跟踪[J]. 计算机科学 , 2012, 39 (8) : 296-299 WANG Aixia, LI Jingjiao, WANG Qing, et al. Target tracking based on multi-core parallel particle filtering[J]. Computer Science , 2012, 39 (8) : 296-299 |
| [5] | GORDON N, SALMOND D J, SMITH A F M. Novel approach to nonlinear/non-Gaussian Bayesian state estimation[C]//IEE Proceedings of Radar and Signal Processing. Cambridge, UK: IEE, 1993: 107-113. |
| [6] | DOUCET A, GODSILL S. On sequential Monte Carlo sampling methods for Bayesian filtering[J]. Statistics and Computing , 2000, 10 (1) : 197-208 |
| [7] | DING Xiaofeng, XU Lizhong, WANG Xin. Roubust visual object tracking using covariance features in quasi-Monte Carlo filter[J]. Intelligent Automation and Soft Computing , 2011, 17 (5) : 571-582 DOI:10.1080/10798587.2011.10643171 |
| [8] | 华罗庚, 王元. 数论在近似分析中的应用[M]. 北京: 科学出版社, 1978 : 22 -26. |
| [9] | GUO D, WANG X D. Quasi-Monte Carlo filtering in nonlinear dynamic systems[J]. IEEE Transactions on Signal Processing , 2006, 54 (6) : 2087-2098 DOI:10.1109/TSP.2006.873585 |
| [10] | WANG Y, FANG K T. Number-theoretic methods in statistics[M]. New York: Chapman & Hall, 1994 : 20 -25. |
| [11] | 陈志敏, 薄煜明, 吴盘龙, 等. 拟蒙特卡罗粒子滤波改进算法及其在雷达目标跟踪中的应用[J]. 应用科学学报 , 2012, 30 (6) : 607-612 CHEN Zhimin, Bo Yuming, WU Panlong, et al. Improved quasi-Monte-Carlo particle filtering and its application to radar target tracking[J]. Journal of Applied Sciences , 2012, 30 (6) : 607-612 |
| [12] | 徐立中, 丁晓峰, 王鑫, 等. 基于信赖域的序贯拟蒙特卡罗滤波算法[J]. 电子学报 , 2011, 39 (3A) : 24-29 XU Lizhong, DING Xiaofeng, WANG Xin, et al. Trust region based sequential quasi-Monte Carol filter[J]. Acta Electronica Sinica , 2011, 39 (3A) : 24-29 |
| [13] | 李安平.复杂环境下的视频目标跟踪算法研究[D].上海:上海交通大学, 2006: 20-31. LI ANPING. Research of tracking algorithm for visual target under complex environments[D]. Shanghai:Shanghai Jiao Tong University, 2006: 20-31. |
| [14] | KATJA N, ESTHER K, LUC V G. Object tracking with and adaptive color based particle filter[C]//Proceedings of the 24th DAGM Symposium on Pattern Recognition. Zurich, Switzerland, 2002: 353-360. |
| [15] | 方正, 佟国峰, 徐心和. 粒子群优化粒子滤波方法[J]. 控制与决策 , 2007, 22 (3) : 273-277 FANG Zheng, TONG Guofeng, XU Xinhe. Particle swarm optimized particle filter[J]. Control and Decision , 2007, 22 (3) : 273-277 |



