2. 广东工业大学 自动化学院,广东 广州 510090
2. School of Automation, Guangdong University of Technology, Guangzhou 510090, China
重建位于同一张平表面上的三维空间点,这对于室内场景以及一些建筑场景是很常见的情形。传统的方法是先重建出三维空间点[1-2],再用这些三维空间点去拟合场景中的平表面[3-4]。此方法存在2个缺陷:1)重建三维空间点时,没有利用这些三维空间点位于一个平表面上这一先验知识;2)在拟合景物平表面时,需测量三维空间点之间距离的大小,在射影空间中,三维空间点之间的距离没有物理意义。针对这些缺陷,文献[5]将三维空间点约束到一个已知平表面上,并将问题转化为一个8次多项式进行求解。文献[6]考虑到三维点位于景物平表面的约束条件,针对场景平表面已知与景物平表面未知2种情形,给出了恢复三维景物平表面的方法,但不能保证获得全局最优。文献[7]利用场景平表面与单应矩阵之间的关系,通过求解单应矩阵来求解场景平面,由于单应矩阵的转移误差函数是拟凸函数,可以利用最小化L∞范数方法估计单应矩阵,继而恢复景物平表面,利用L∞方法能够得到全局最优值,缺点是计算效率较低,且对局外点敏感。另外,文献[5-7]都是针对2幅图像的三维场景平表面重建,且不能推广到多幅图像。因为考虑三维点位于一张已知的景物平表面上,则对应点集的反向投影线不仅要相交,而且要相交于一个平表面上,以此为约束条件,给出最小化反投影误差的重建法和最小化转移误差的重建法,并采用GA算法进行了最小化求解。采用最小化反投影误差的平表面重建法记为“RPE-GA”(reverse projection error-GA)法,采用最小化转移误差的平表面重建法记为“TE-GA”(transfer error-GA)法,实验结果证明了所提方法的优越性。
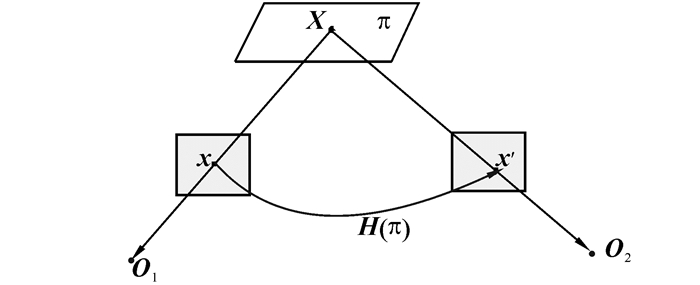
1 基于两视图的三维景物中平表面重建如图 1所示,一张景物平表面上的点的图像点与在第2幅视图上的对应图像点由一个单应矩阵相关联,事实上,这一景物平表面诱导了2幅视图之间的一个单应矩阵。来自空间不同景物平表面的图像对应点之间满足不同的平面单应约束。
|
| 图 1 由景物平表面诱导的单应矩阵H(π) Fig. 1 The homography H(π) induced by a scene plane |
若xi=[ui vi 1]T,x′i=[u′i v′i 1]T是空间平表面上的点在2幅图像上的对应点对,π为未知景物平表面,空间景物平表面参数化为
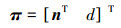 |
式中:n∈R3(法向量),0≠d∈R。则存在矩阵H(π)使得
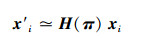 |
式中:
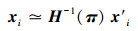 |
若两视图投影矩阵为
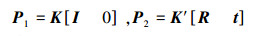 |
则单应矩阵H(π)表示为
 |
证明 为计算H(π),把第1幅视图上的点反向投影且确定该射线和平面π=[nT d]T的交点X,然后再把这个3-D点X投影到第2幅视图上。对第1幅视图有
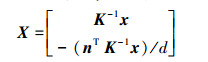 |
3-D点X投影到第2幅图像上可得到
 |
由此,可得
若不存在噪声干扰和误匹配,一般通过最小化几何误差来找到一个单应矩阵H(π),即可求得空间平面参数π,若
 |
则最小化几何误差函数表示为
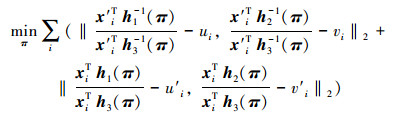 |
这种方法的目标函数为L2范数,所以称之为L2方法,缺陷是容易陷入局部最优。将求解单应矩阵的问题转换为最小化L∞范数进行求解,即最小化最大转移误差来求解,表示为
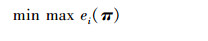 |
式中:ei(π)是转移误差函数,可表示为
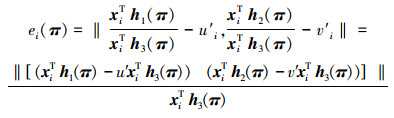 |
(1) |
可证明式(1)在给定子集C={π; xiTh3(π)>0上是一个拟凸函数[8],当范数取2范数时,可以转换为二阶锥规划问题进行求解;当范数取1范数或者∞范数时,可以转化为线性规划问题进行求解。利用二分搜索在公开的软件包SeDuMi上进行求解π的参数值,由此来恢复三维景物平表面。最小化L∞方法可获得最优解,只是这种方法的计算效率比较低,对局外点比较敏感,且基于这种单应矩阵转移误差的方法只局限于2幅图像的三维景物平表面重建。
2 基于多视图的三维景物中平表面重建三维景物中平表面重建意味着重建后的空间点应位于同一个平面内。换言之,三维景物中平表面重建就是以重建的空间点在同一个平面内为约束条件的寻优问题。采用基于最小化反投影误差的平表面重建法记为“RPE-GA”,采用基于最小化转移误差的平表面重建法记为“TE-GA”。
2.1 基于最小化反投影误差的平表面重建模型若已经得到多视图所对应的摄像机投影矩阵Pi, i=1, 2,…, M和对应匹配点集,设任意空间点齐次坐标为
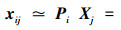
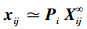
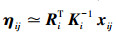
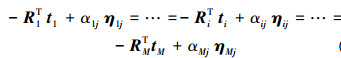 |
(2) |
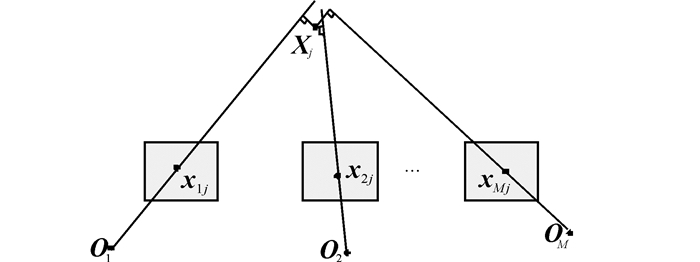
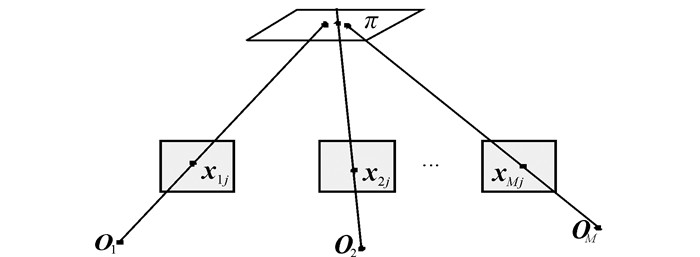
由于在图像点检测与匹配的过程中,不可避免地存在误差,所以这些反投影直线并不相交于一点,如图 2所示。一般的求解方法是通过最小化点到所有反投影直线的距离平方和来得到最优解Xj,但这种方法只适用于欧氏空间或者准欧氏空间,如果未得到摄像机的标定参数,即仅仅在射影空间中进行三维重建,此时欧氏距离并没有实际的物理含义,因此不能保证此方法的最优性。因此很多文献[9-12]都是将误差转移到图像平面上(即欧氏空间中)进行最小化重投影误差来求解的。本文是针对景物中的平表面进行重建,由于误差的存在,反向投影线虽然也不交于一点,但反向投影线都应与一个空间平面相交,如图 3所示。因为反投影线都与一个场景平面π相交,且所求空间点也位于场景平面π上,因此平表面重建可以通过最小化平表面上的反投影误差进行求解,表示为
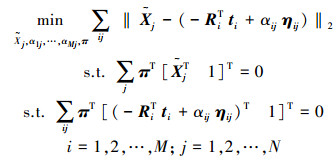 |
(3) |
|
| 图 2 反投影线不交于一点 Fig. 2 Reverse projection lines don't intersect in a point |
|
| 图 3 反向投影线与一个空间平面相交 Fig. 3 Reverse projection lines intersect in a scene plane |
约束方程πT[[-RiTti+αijηij]T 1]T=0表示反投影线与平表面相交于一点,而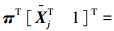
为了降低问题求解的复杂度,可利用空间景物平面与图像平面之间的单应转移关系,从而通过在空间景物平面上最小化转移误差进行求解。若多视图投影矩阵为P1=K1[R1 t1],Pi=Ki[Ri ti],…,PM=KM[RM tM],平面π上一个空间点坐标为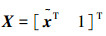
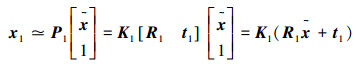 |
由于空间点X位于平面π上,所以πTX=0,则有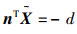
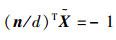
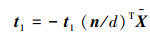
 |
因此,平面π到第1个图像平面的单应矩阵为H1=K1(R1-t1(n/d)T)。同理,在第2个摄像机下的投影表示为
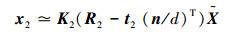 |
则平面π到第2个图像平面的单应矩阵为H2=K2(R2-t2(n/d)T)。以此类推,平面π到第i个图像平面的单应矩阵为Hi=Ki(Ri-ti(n/d)T)。若摄像机矩阵已知,则空间场景平面与图像平面之间的单应矩阵是一个关于未知量π的矩阵,记为Hiπ,单应矩阵总是将二维空间点齐次映射到二维空间点上,因此它是一个3×3的可逆矩阵。则对于第j个空间点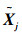
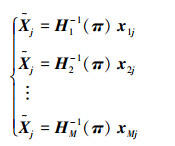 |
而由于存在误差,所以实际要求的空间点
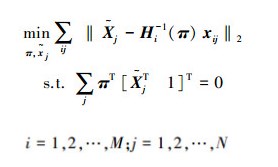 |
(4) |
由于可以很明显地看出,式(4)较式(3)少了未知参数αij,求解相对简单一些。式(4)是利用二维图像平面与二维空间平面之间的转移矩阵(即单应矩阵Hi(π))将误差转移到空间平表面上进行最小化的。而式(3)是通过限制反投影线与空间平面相交且交于一点,从而将误差转移到空间平面上最小化求解。总而言之,无论最小化反投影误差的平表面重建法,还是最小化转移误差的平表面重建法,都是将误差转移到空间平表面上进行最小化求解的,这2种方法的基本原理一致。
2.3 基于多视图的三维景物中平表面重建式(3)和式(4)都是有约束的优化问题,对于有约束的最小化问题,可以引入罚函数构造增广代价函数,将给定的约束优化问题转化为一系列无约束优化问题,然后通过求解这一系列的无约束优化问题而获得原约束优化问题的解。惩罚法有多种类型,常用的有:外惩罚法(又称罚函数法)和内惩罚法(又称障碍函数法)。采用罚函数法,如果约束优化问题为
 |
(5) |
记可行域为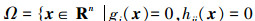
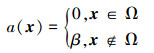 |
式中:β为惩罚因子,表示对不可行点的惩罚。然后,将原问题转换为求解下列无约束优化问题:
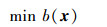 |
(6) |
式中:
称式(6)为式(5)的增广代价函数。由于β是一个非常大的数,所以函数b(x)的解也一定是原问题的解。
先将式(3)和式(4)转换为无约束问题,再采用遗传算法(GA)进行求解,遗传算法是一个非常成熟的计算工具,这里不再详细介绍。本文的创新之处是建立了2种平表面重建模型,而不是针对遗传算法的改进。另外,由法向量n中的3个参数足以确定一个平面,所以在实际计算过程中令d=1。
基于多视图的三维景物中平表面重建步骤为:
1)输入N个空间点对应的图像点数据,摄像机的投影矩阵Pi, i=1, 2, …, M;
2)将式(4)和式(3)转换为如式(6)所示的无约束优化函数,设置惩罚因子β=500,即构造关于式(4)和式(3)的适应度函数;
3)初始化种群,每一个染色体都是N个空间点和场景平面法线向量n,以及参数αij(见式(3))的组合,采用实数编码,设定种群个数,即染色体个数Nind=50,并设置边界条件;
4)选择操作,计算种群中每个染色体的适应度值,采用轮盘赌的方法进行选择复制,即各个染色体按照适应度值所占总适应度值的比例组成面积为1的一个圆盘,指针转动停止之后,指向的染色体将被复制到下一代,适应度好的染色体被选择的概率大,每个染色体被选中的概率为
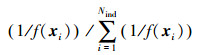 |
式中:f(xi)代表适应度值,Nind代表染色体个数;
5)交叉操作,以交叉概率pc=0.6进行一点交叉,把2个父代个体的部分基因进行交换而生成新的个体,直到所有个体都被选择过;
6)变异操作,选变异概率pm=0.02,即全部染色体位串上的每位基因按变异概率pm进行随机改变;
7)保存当前适应度函数的最小值,以及对应的染色体位置;
8)直至达到最大迭代次数,最大迭代次数为100,若满足,则停止迭代,否则转4);
9)输出当前适应度函数最小值对应的最优染色体,即空间点的最优坐标值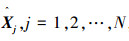
采用2.6 GHz Pentium Dual-Core CPU,2 GB内存的台式电脑,并在MATLAB 7.0环境下进行了2组实验,分别是仿真数据实验和真实图像实验。并对式(3)和式(4)利用GA算法进行了优化计算,采用式(3)记为“RPE-GA”法,采用式(4)记为“TE-GA”法。为了进行对比,利用传统法进行实验,首先重建出三维空间点,然后拟合一个平表面,在传统法中利用L∞方法[11]进行多视图的重建,L∞方法可以获得全局最优解,因此将这种方法记为“L∞”法。实验中采用的性能参数为:重投影均方根误差为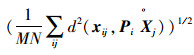
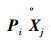
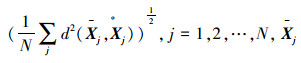
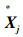
仿真实验中需要知道产生检测数据的真正平表面参数,设置如下:将平表面定为Xw-Yw平表面,即Zw=0平表面,随机生成范围在[-1, 1]内的100个点,即N=100,要保证这些点在每个摄像机下都是可视的。假设用6个摄像机进行拍摄,实验中每台摄像机的内参数设为
 |
设定每个摄像机之间大概相差10°,图像分辨率为640×480。仿真实验环境如图 4所示,图 4中用圆圈来表示摄像机的位置,点云为随机生成的Zw=0平表面上的点。

|
| 图 4 仿真实验环境示意图 Fig. 4 The schematic diagram of simulation environment |
在每个图像点上增加零均值、标准差为σ的高斯噪声,噪声大小分别为0.2、0.4、0.6、0.8、1.0个像素,对每种噪声分别进行100次实验。由于对带有噪声的数据都进行了100次实验,每次实验都会产生一个重建结果,数据过多,不再列出,只给出3种平表面重建方法的性能比较,如表 1所示。从表 1可以看出,RPE-GA法和TE-GA法的精度基本一致,可以明显看出空间位置均方根误差比较小,这是因为是通过最小化的空间点位置误差进行优化求解的,所以空间位置均方根误差较小;而L∞方法的重投影均方根误差较小,这是因为在L∞法中是通过最小化图像平面上的重投影误差进行优化求解的,所以重投影均方根误差较小。由于在L∞法中没有考虑到景物平表面的约束,所以空间位置均方根误差较大,也就与真实的景物平表面相差较远。
| 方法 名称 |
噪声 标准差(σ) |
重投影均 方根误差 |
空间位置 均方根误差 |
| 0.2 | 0.013 0 | 0.005 1 | |
| 0.4 | 0.017 1 | 0.016 2 | |
| L∞ | 0.6 | 0.020 1 | 0.0183 |
| 0.8 | 0.031 1 | 0.025 1 | |
| 1.0 | 0.045 2 | 0.038 3 | |
| 0.2 | 0.020 1 | 0.000 8 | |
| 0.4 | 0.063 3 | 0.001 1 | |
| RPE-GA | 0.6 | 0.085 2 | 0.001 3 |
| 0.8 | 0.096 4 | 0.0017 | |
| 1.0 | 0.104 2 | 0.002 3 | |
| 0.2 | 0.018 4 | 0.000 7 | |
| 0.4 | 0.059 4 | 0.001 0 | |
| TE-GA | 0.6 | 0.083 3 | 0.001 4 |
| 0.8 | 0.095 4 | 0.001 6 | |
| 1.0 | 0.109 1 | 0.002 0 |
3.2 真实图像实验与结果分析
真实图像实验采用Zhang从不同角度拍摄平面模版的5幅图像(http://research.microsoft.com/en-us/um/people/zhang/calib/),如图 5所示,图像分辨率大小为640×480,平面模版上共有256个角点,即N=256。

|
| 图 5 平面模版的5幅图像 Fig. 5 Five images of a planer pattern |
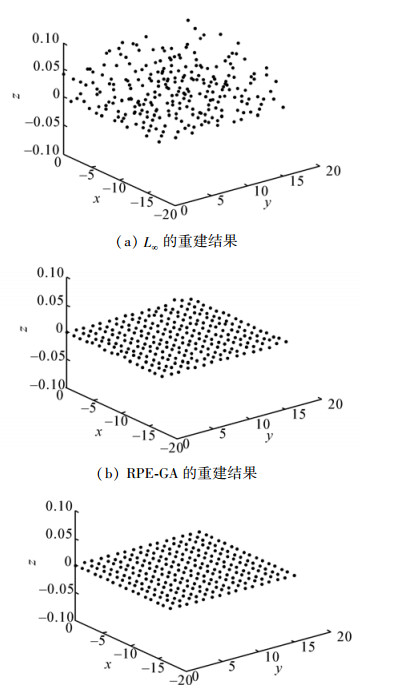
真实图像的重建结果如图 6所示。从图 6可以看出本文方法的重建结果基本上位于一个平表面上,而传统的L∞法重建结果非常散乱,并不位于一个平表面上。真实图像实验中3种重建平表面方法的性能比较如表 2所示。同样的,RPE-GA法和TE-GA法的空间位置均方根误差比较小,与真实的景物平表面相接近;而L∞法的重投影均方根误差较小,但空间位置均方根误差却比较大,也就是与真实的景物平表面相差较远。从原理上来讲,RPE-GA和TE-GA 2种优化方法是一样的,都是将空间点限制在一个平表面上,然后最小化空间点之间的距离误差,所以它们的精度基本一致。只是由于RPE-GA法中多了参数αij,所以RPE-GA法的计算会比TE-GA法复杂。本文方法的优越性:1)利用三维空间点都位于同一个景物平表面这一先验知识,计算出的平表面精度较高;2)可以推广到多幅视图。
|
| 图 6 平面模版的重建结果 Fig. 6 Reconstruction of the planar pattern |
| 方法名称 | 重投影均方根误差 | 空间位置均方根误差 |
| L∞ | 0.063 5 | 0.058 3 |
| RPE-GA | 0.081 2 | 0.001 3 |
| TE-GA | 0.081 5 | 0.001 2 |
需要指出的是RPE-GA法和TE-GA法对局外点都比较敏感,事实上,目前已有的基于两视图景物平表面重建方法,如Olsson[7]提出的重建方法对局外点也比较敏感。如果用在场景比较复杂的真实图像实验中,会存在2类局外点,一类是在匹配错误的点,一类是不位于一个平表面上的点。首先需要采用一些剔除局外点的方法对局外点进行剔除,Olsson采用L1方法对局外点进行了剔除,但是从实验结果中可以很明显的看出,即使对局外点进行了剔除,仍然有很多图像点不位于同一个平表面上,用这些不位于同一个平表面上的图像点去重建一个平表面势必是不准确的。
5 结束语在传统的三维景物中平表面重建法中,都是先重建出三维点,再用这些三维点去拟合景物平表面,由于没有利用三维空间点位于一个平表面的先验知识,所以重建出的三维点并不位于一个平表面上。针对这个问题,本文提出了2种三维景物中平表面重建模型,2种模型都是考虑到重建的空间点应位于同一个平面内,以此为约束条件分别在空间平面上进行最小化反投影误差和最小化转移误差,再采用GA算法对2种模型进行了优化求解,从而获得平表面重建结果。实际上,基于最小化反投影误差的平表面重建法和基于最小化转移误差法的平表面重建法基本原理相同,只是计算复杂度不同。实验表明了本文方法的优越性。另外如何剔除掉局外点,或者说如何从复杂场景中提取出位于一个平表面上的图像点,将RPE-GA法和TE-GA法用于复杂场景的真实图像实验上,将是未来需要研究的问题。据知,目前在国内外考虑三维点位于空间景物平面的约束条件,针对多视图的三维景物中平表面重建的研究还处于空白。
| [1] | LINDSTROM P. Triangulation made easy[C]//Proceedings of IEEE Conference Computer Vision Pattern Recognition. San Fransico, USA, 2010: 1554-1561. |
| [2] | TOSSAVAINEN T. Approximate and SQP two view triangulation[C]//Proceedings of 10th Asian Conference Computer Vision. Queenstown, New Zealand, 2010, 3: 1303-1316. |
| [3] | HARTLEY R, ZISSERMAN A. Multiple view geometry in computer vision[M]. Cambridge: Cambridge University Press, 2003 : 54 -57. |
| [4] | ZACH C, SORMAN M, KARNER K. High-performance multi-view reconstruction[C]//Proceedings of the Third International Symposium on 3D Data Processing, Visualization, and Transmission. Chapel Hill, North Carolina, USA, 2006: 113-120. |
| [5] | CHUM O, PAJDLA T, STURM P. The geometric error for homographies[J]. Computer Vision and Image Understanding , 2002, 97 (1) : 86-102 |
| [6] | KANATANI K, NIITSUMA H. Optimal two-view planar scene triangulation[J]. IPSJ Transactions on Computer Vision and Applications , 2011, 3 : 67-79 DOI:10.2197/ipsjtcva.3.67 |
| [7] | OLSSON C, ERIKSSON A. Triangulating a plane[C]//Proceedings of Scandinavian Conference on Image Analysis. Berlin Heidelberg, Germany, 2011: 13-23. |
| [8] | KE Q, KANADA T. Quasiconvex optimization for robust geometric reconstruction[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence , 2007, 29 (10) : 1834-1847 DOI:10.1109/TPAMI.2007.1083 |
| [9] | AGARWAL S, SNAVELY N, SEITZ S M. Fast algorithms for L-infinity problems in multiview geometry[C]//Proceeding of IEEE Computer Society Conference on Computer Vision and Pattern Recognition. Anchorage, Alaska, USA, 2008: 24-26. |
| [10] | HARTLEY R, KAHL F, OLSSON C, et al. Verifying globle minima for L2 minimization problems in multiple view geometry[J]. International Journal of Computer Vision , 2013 : 288-304 |
| [11] | KAHL F, HARTLEY R. Multiple-view geometry under the L-infinity norm[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence , 2008, 30 (9) : 1603-1617 DOI:10.1109/TPAMI.2007.70824 |
| [12] | LEE H, SEO Y, LEE S W. Removing outliers by minimizing the sum of infeasibilities[J]. Image and Vision Computing , 2010, 28 : 881-889 DOI:10.1016/j.imavis.2009.11.004 |



