1965年Zadeh首次提出了模糊集的概念,随后人们相继给出了模糊集的一些推广形式,例如Atanassov的直觉模糊集以及区间直觉模糊集[1],就是对Zadeh模糊集理论的一种扩充和发展。1982年Pawlak提出了粗糙集[2]的概念,由于模糊集和粗糙集理论在处理不确定性和不精确性问题方面都推广了经典集合论,因此将2个理论相融合,建立模糊粗糙集成为信息领域研究的主要方向之一。许多学者致力于这方面的研究,提出了各种广义的粗糙模糊集或模糊粗糙集以及粗糙(区间)直觉模糊集[3]或(区间)直觉模糊粗糙集。模糊熵[4]是模糊集理论中一个重要的研究对象,用来刻画模糊集的不确定性,许多学者从不同角度对各种广义模糊集的熵进行了深入的研究,分别给出了模糊熵、直觉模糊熵[5-7]、Vague熵以及区间直觉模糊熵[8-10]的公理化定义和计算公式。Mi[4]利用一种新的模糊熵,研究了粗糙模糊集的不确定性度量。但对粗糙区间直觉模糊集不确定性度量的研究,目前研究很少,所以本文试图通过先定义区间直觉模糊集的粗糙隶属函数,然后再利用现有的区间直觉模糊熵公式,给出粗糙区间直觉模糊集的不确定性度量,但发现文献[10]中的熵公式存在一定的问题:当区间直觉模糊集退化为普通模糊集时,利用文中公式计算所得的熵均为零,这显然是不合逻辑的。因此本文参考文献[7],给出了基于三角函数的区间直觉模糊熵公式,并在此基础上讨论了粗糙区间直觉模糊集的不确定性度量方法。
1 粗糙区间直觉模糊集的基本理论定义1[1] (区间直觉模糊集)设U是一个非空经典集合,D[0, 1]是区间[0, 1]上所有闭子区间所构成的集合,称U上形如A={〈x, μA(x), vA(x)〉|x∈U}的三元组为U上的一个区间直觉模糊集。其中,μA:U→D[0, 1]和vA:U→D[0, 1]分别表示U上元素x属于A的隶属度和非隶属度,0≤sup μA(x)+sup vA(x)≤1,∀x∈U.
为方便,将区间直觉模糊集A记为
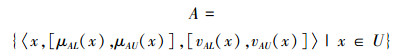 |
U上所有区间直觉模糊集构成的集合为IVIF(U).
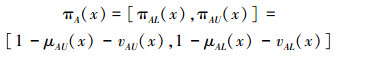 |
称为x属于A的区间直觉模糊指数。
定义2[11] 设ai∈[0, 1], i∈J, J={1, 2,…, m},定义
 |
特别地,对[ai, bi]∈D[0, 1]i=1, 2,定义
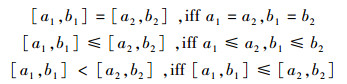 |
且[a1, b1]≠[a2, b2]
定义3[12] 设U是一个非空经典集合,A, B∈IVIF(U),∀x∈U规定序及运算如下:
1) A⊆B iff μA(x)≤μB(x)且vA(x)≥vB(x);
2) A=B iff μA(x)=μB(x)且vA(x)=vB(x);
3)~A={〈x, vA(x), μA(x)〉|x∈U}.
下面本文均假定U是非空有限论域,且U={x1, x2, …, xn}。
定义4[3] 设(U, R)是Pawlak近似空间,即R是U上的等价关系。∀A∈IVIF(U),则A在近似空间(U, R)的下近似R(A)、上近似R(A)是一对区间直觉模糊集:
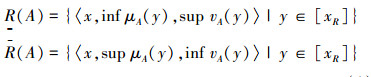 |
(1) |
式中:[x]R={y∈U|(x, y)∈R}表示x所在的R等价类。序对(R(A), R(A))称为粗糙区间直觉模糊集。若R(A)=R(A),则称A是可定义的。
2 区间直觉模糊集的粗糙隶属函数本小节首先将文献[4]中模糊集粗糙隶属函数的定义推广到区间直觉模糊集。
定义5 设(U, R)是Pawlak近似空间,对∀A∈IVIF(U),则A的粗糙隶属函数R(A):IVIF(U)→IVIF(U)定义为
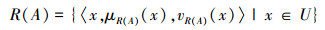 |
(2) |
式中:
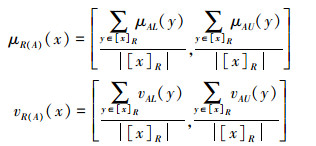 |
定理1 设(U, R)是Pawlak近似空间,区间直觉模糊集的粗糙隶属函数具有性质:
1) ∀A, B∈IVIF(U),若A⊆B,则R(A)⊆R(B);
2)若A∈IVIF(U),则R(~A)=~R(A)。
证明 由定义5和区间直觉模糊集的序及运算直接即可验证。
3 区间直觉模糊熵对熵的研究目前主要集中在Fuzzy集、Vague集和直觉模糊集上,对区间直觉模糊集的模糊熵研究还较少。文献[8]给出了区间直觉模糊熵的公理化定义,但未给出具体的区间直觉模糊熵公式,文献[9]在此基础上构造了一种区间直觉模糊熵公式。文献[10]中指出文献[8]中的区间直觉模糊熵的公理化定义存在缺陷,并因此对其进行了改进,同时考虑了区间直觉模糊集的犹豫度和区间跨度所产生的模糊度。但文献[10]中给出的区间直觉模糊熵公式仍然存在严重缺陷:当区间直觉模糊集退化为普通模糊集时,利用文中公式计算所得的熵均为零,即任意模糊集的熵都为零,这显然是不合逻辑的。所以本文认为还是文献[8]给出的公理化定义更趋合理,当隶属度区间和非隶属度区间相同时,无论犹豫度多大,所产生的模糊度都应达到最大值。文献[7]基于Ye[13]提出的基于三角函数的直觉模糊熵公式,给出了一个更合理的基于三角函数的直觉模糊熵公式,本文将这一结果推广到区间直觉模糊集,构造一个基于三角函数的区间直觉模糊熵公式。
定义6[8] 称映射E:IVIF(U)→[0, 1]为区间直觉模糊集的一个区间直觉模糊熵。对∀A∈IVIF(U),如果E满足如下条件:
1) E(A)=0当且仅当A是一个分明集;
2) E(A)=1当且仅当对∀x∈U都有μA(x)=vA(x);
3) E(A)=E(~A);
4)对∀x∈U及∀A, B∈IVIF(U),如果当μB(x)≥vB(x)时,有A⊇B,或当μB(x)≤vB(x)时,有A⊆B,则E(A)≤E(B).
定理2 对∀A∈IVIF(U),定义
 |
(3) |
则由(3)式定义的E是一个区间直觉模糊熵。
证明 要证由(3)式定义的E是一个区间直觉模糊熵,只需证明该公式满足定义6中的条件1)~4)。
式(3)中,令
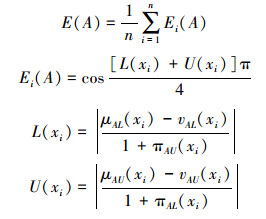 |
则由0≤μAL(xi)≤1, 0≤vAL(xi)≤1, 0≤μAU(xi)≤1, 0≤vAU(xi)≤1, 得0≤L(xi)≤1, 0≤U(xi)≤1,即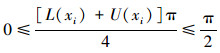
条件1 设A是一个分明集,即对∀xi∈U都有μA(xi)=[0, 0], vA(xi)=[1, 1]或μA(xi)=[1, 1], vA(xi)=[0,0]。无论哪种情况都有Ei(A)=0,因此,E(A)=0。反之,若E(A)=0,则由0≤Ei(A)≤1和式(3)可知Ei(A)=0。又因为
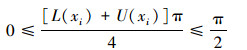 |
因此
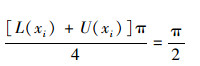 |
则有L(xi)+U(xi)=2,又因为0≤L(xi)≤1,0≤U(xi)≤1,所以需有L(xi)=1, U(xi)=1,由此可得μA(xi)=[1, 1], vA(xi)=[0,0]或μA(xi)=[0, 0],vA(xi)=[1, 1]。
所以A是一个分明集。
条件2 设对∀xi∈U都有μA(xi)=vA(xi),则Ei(A)=1,所以E(A)=1。
反之,若设E(A)=1,则由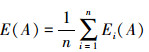
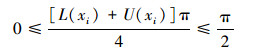 |
需有L(xi)+U(xi)=0,再由0≤L(xi)≤1, 0≤U(xi)≤1,则有L(xi)=0, U(xi)=0,因此有μA(xi)=vA(xi)。
条件3 由~A={〈x, vA(x),μA(x)〉|x∈U}和式(3)易得,
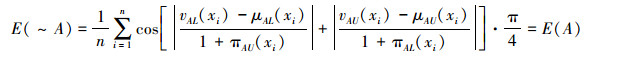 |
条件4 设对∀xi∈U,当μB(xi)≥vB(xi)时,有A⊇B,即μBL(xi)≥vBL(xi),μBU(xi)≥vBU(xi)时,有μAL(xi)≥μBL(xi), μAU(xi)≥μBU(xi),vAL(xi)≤vBL(xi), vAU(xi)≤vBU(xi)。
由文[7]中定理1的证明过程可知有: 
所以有
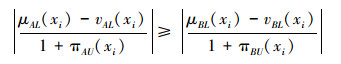 |
同理有
 |
所以
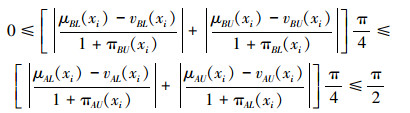 |
(4) |
当μB(xi)≤vB(xi)时,有A⊆B时,同理可证
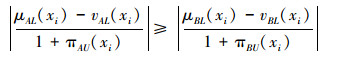 |
同理有
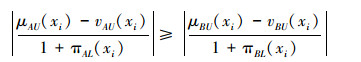 |
即式(4)仍成立。由余弦函数在[0, π/2]上的单调性易得,对∀xi∈U,有Ei(A)≤Ei(B),故E(A)≤E(B)。
综上可知E是一个区间直觉模糊熵。
4 粗糙区间直觉模糊集的不确定性度量定义7 设(U, R)是Pawlak近似空间,A∈IVIF(U),则粗糙区间直觉模糊集(R(A), R(A))的模糊性度量IVIFR(A)定义为粗糙隶属函数的区间直觉模糊熵:
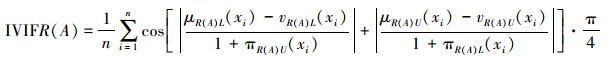 |
(5) |
定理3 设(U, R)是Pawlak近似空间,A∈IVIF(U),则IVIFR(A)=0当且仅当A是经典集合且是可定义的。
证明 设A是经典集合且是可定义的,则R(A)=A=R(A)。分2种情况讨论:
1) ∀x∈A,有[1, 1]=μA(x)=μ R(A)(x)=inf{μA(y)|y∈[x]R},因此∀y∈[x]R都有μA(y)=[μAL(y), μAU(y)]=[1, 1],即
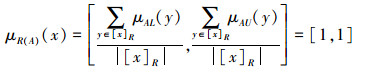 |
此时显然有vR(A)(x)=[0, 0]。
2)∀x∉A,有[1, 1]=vA(x)=v R(A)(x)=inf{vA(y)|y∈[x]R},因此y∈[x]R都有vA(y)=[vAL(y), vAU(y)]=[1, 1],即
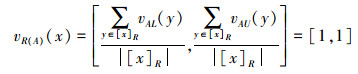 |
此时显然有μR(A)(x)=[0, 0]。
由(1),(2)和定义7可知,∀x∈U,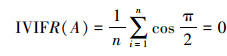
反之,对∀x∈U,若IVIFR(A)=0,由定理2条件1的证明过程可知,应有μR(A)(x)=[1, 1],vR(A)(x)=[0, 0]。再由定义5及0≤μAL(y)≤1, 0≤μAU(y)≤1,0≤vAL(y)≤1, 0≤vAU(y)≤1,可知对∀y∈[x]R,都有μA(y)=[1, 1],vA(y)=[0, 0]。由定义4和x∈[x]R,可得μA(x)=μ R(A)(x)=μR(A)(x)=[1, 1],vA(x)=v R(A)(x)=vR(A)(x)=[0, 0]。即A是经典集合且是可定义的。
定理4 设(U, R)是Pawlak近似空间,则A∈IVIF(U),有IVIFR(~A)=IVIFR(A)。
证明 由定理1可知R(~A)=~R(A)。即R(~A)={〈x, vR(A)(x), μR(A)(x)〉|x∈U}。再由公式(5)直接可得IVIFR(~A)=IVIFR(A)。
定理3和定理4表明当且仅当对于经典可定义集合,其粗糙区间直觉模糊性度量等于零,一个区间直觉模糊集和它的余集的粗糙区间直觉模糊性度量是相等的。
5 结束语本文首先定义了区间直觉模糊集的粗糙隶属函数并讨论其性质,然后给出了一种基于三角函数的区间值直觉模糊集的熵,在此基础上讨论了粗糙区间直觉模糊集的模糊性度量。由于区间直觉模糊集的粗糙隶属函数和熵有各种不同的定义方式,因此本文只是讨论了其中的一种,但这种度量具有很好的性质,它在不确定性分析方面的具体应用值得进一步深入研究。
| [1] | ATANASSOV K. Intuitionistic fuzzy sets[J]. Fuzzy Sets and Systems , 1986, 20 (2) : 87-96 |
| [2] | PAWLAK Z. Rough sets[J]. International Journal of Computer Information Science , 1982, 5 : 341-356 |
| [3] | ZHANG Zhiming. An interval-valued rough intuitionistic fuzzy set model[J]. International Journal of General Systems , 2010, 1 : 135-164 |
| [4] | 张文修, 姚一豫, 梁怡. 粗糙集与概念格[M]. 西安: 西安交通大学出版社, 2006 : 14 -16. |
| [5] | BURILLO P, BUSTINCE H. Entropy on intuitionistic fuzzy sets and on interval-valued fuzzy sets[J]. Fuzzy Sets and Systems , 2001, 118 (3) : 305-316 |
| [6] | SZMIDT E, KACPRZYK J. Entropy for intuitionistic fuzzy sets[J]. Fuzzy Sets and Systems , 2001, 118 (3) : 467-477 DOI:10.1016/S0165-0114(98)00402-3 |
| [7] | 魏翠萍, 高志海, 郭婷婷. 一个基于三角函数的直觉模糊熵公式[J]. 控制与决策 , 2012, 27 (4) : 571-574 WEI Cuiping, GAO Zhihai, GUO Tingting. An intuitionistic fuzzy entropy measure based on thetrigonometric function[J]. Control and Decision , 2012, 27 (4) : 571-574 |
| [8] | 郭效之.模糊不确定性度量的探讨及扩展[D].西安:西北大学, 2004: 48-50. |
| [9] | 王培, 魏翠萍.一种区间直觉模糊熵的构造方法[J].计算机工程与应用, 2011, 47(2): 43-46. Constructing method of Interval-valued intuitionistic fuzzy entropy[J]. Computer Engineering And Applications, 2011, 47(2):43-46. |
| [10] | 屈克, 汤磊, 荣文静.区间直觉模糊集熵的构造及其基本性质[J].重庆文理学院学报:自然科学版, 2010, 29(3):21-24. QU Ke, TANG Lei, RONG Wenjing. The construction and basic properties of entropy ofi nterval-valued i ntui tionisti c fuzz y sets[J]. |
| [11] | GONG Z T, SUN B Z, CHEN D G. Rough set theory for interval-valued fuzzy information systems[J]. Information Sciences , 2008, 178 : 1968-1985 DOI:10.1016/j.ins.2007.12.005 |
| [12] | ATANASSOV K. Operators over interval valued intuitionistic fuzzy sets[J]. Fuzzy Sets and Systems , 1994, 64 : 159-174 DOI:10.1016/0165-0114(94)90331-X |
| [13] | YE Jun. Two effective measures of intuitionistic fuzzy entropy[J]. Computing , 2010, 87 (1/2) : 55-62 |



