减摇鳍是船舶不可缺少的减摇装置,主要用于船舶的横摇减摇。如何降低航行成本是船舶减摇装置的新趋势。减摇装置能量损失[1]主要包括减摇系统自身工作消耗的能量和减摇系统工作影响船舶运动姿态间接对航行阻力影响而主机额外的功率损耗。目前关于减摇鳍的各种控制算法研究都尽可能突出系统减摇效果,而减摇鳍系统能量优化相关研究较少。本文针对减摇鳍系统能量优化的控制要求,提出基于遗传算法多目标优化方法。这样在满足减摇效果相对较好的同时,降低减摇鳍的转角幅度和转角频率[2],有效地降低减摇鳍系统的能量消耗,降低航行成本。
遗传算法在多目标函数优化方面的应用效果明显。在近似分析计算减摇鳍系统负载能耗基础上,建立关于减摇效果以及能量优化多目标函数,采用遗传算法进行多目标优化[3-4],将减摇效果和经济节能有效结合,是对全新减摇系统控制器研究的创新。
1 减摇鳍控制系统组成船舶减摇鳍系统的控制结构如图 1所示。以下是减摇鳍控制系统各相关传递函数以及系统主要组成部分在能量优化中占据的地位。为研究方便,本文选用NJ5减摇鳍模型来说明各部分作用和传递函数。
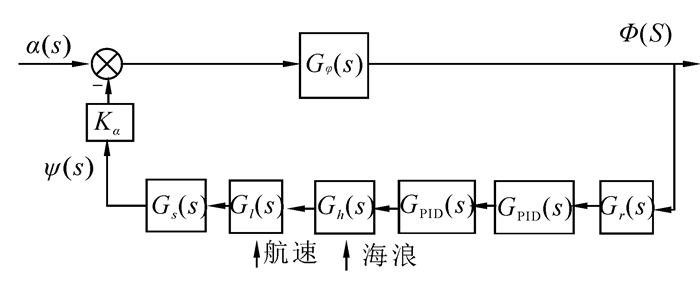
|
| 图 1 减摇鳍控制系统框图 Fig. 1 The fin stabilizer system block diagram |
角速度传感器是船舶航行中减摇鳍系统横摇角速度的测量元件。角速度传感器传递函数为
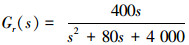 |
NJ5减摇鳍模型中前置放大器传递函数为
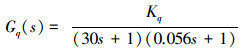 |
式中Kq为可调增益。
在实际工程应用中减摇鳍系统主要采用PID控制,它直接决定系统综合性能指标好坏,即减摇效果和能量优化。PID控制器传递函数[5]为
 |
(1) |
在设定航速和海情下通常将浪级调节器和航速调节器设置为
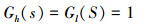 |
随动系统在能量优化性能指标中具有重要作用,由于随动系统驱动减摇鳍定轴转动需要消耗大量能量,尤其当鳍面积越大,能量消耗越多。减摇鳍的随动系统常常采用电液系统,数学模型可近似表示为二阶振荡环节,随动系统传递函数为
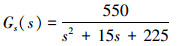 |
Kα由很多因素决定,为研究方便常常将其近似为常量。对NJ5减摇鳍模型,当最大鳍角ψmax取22°时,鳍角到波倾角的转换系数为Kα=0.256,船舶横摇运动传递函数为
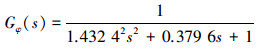 |
当船舶在波浪作用下剧烈摇摆时,将降低主机功率,同时也降低航速,因此减摇鳍系统能量优化和减摇效果必须首先考虑未减摇时船舶横摇角以及减摇后横摇角。实际工程应用表明,横摇角在一定范围内时,可以减小船舶的粘性阻力和破浪阻力,有利于提高主机功率,降低燃油消耗,增加航速,节约成本。因此,减摇鳍系统要综合考虑横摇角范围。从控制效果和稳定性来说,横摇角越小越好。横摇角方差推导过程如下。
由图 1知,以等效波倾角α(s)为输入,以横摇角φ(s)为输出的系统传递函数为
 |
根据随机过程理论,船舶减摇鳍控制系统横摇角谱为
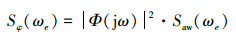 |
式中:Sφ(ωe)为船舶横摇角谱密度,Saw(ω)为海浪等效波倾角谱密度,Φ(jω)为综合减摇系统开环传递函数。
于是,减摇后船舶横摇角方差为
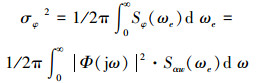 |
所以第1个目标函数为
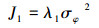 |
式中:σφ2为减摇后船舶横摇角方差,λ1为加权系数。
2.2 减摇鳍鳍角方差的计算减摇鳍系统能量优化和使用寿命也是需要考虑的问题。当减摇鳍鳍角增大到一定程度时,流过鳍的流体就不能沿着鳍的表面而是离开鳍流动,此时鳍失速,并损耗鳍上的部分升力[6-8]。从而影响减摇效果和随动系统的转鳍功率。所以最大工作鳍角是有一定限度的,并且鳍角幅值服从瑞利分布。于是,减摇鳍鳍角ψ超过鳍角ψmax的概率p可表示为
 |
实际工程应用中,最大鳍角ψmax取22°,鳍角饱和率一般不会大于20%[9],将p=20%,ψmax=22°代入式(2)可计算出此时鳍角方差σψ2=150.31。因此,第2个目标函数为
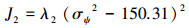 |
(2) |
式中:σψ2为鳍角方差;λ2为加权系数。
由图 1可知,以等效波倾角为输入,鳍角为输出的传递函数为
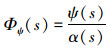 |
以等效波倾角为输入,鳍角速率为输出的传递函数:
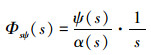 |
鳍角幅值谱密度:
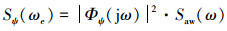 |
鳍角角速率幅值谱密度:
 |
减摇鳍的鳍角方差:
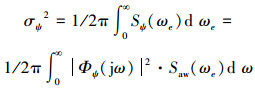 |
在减摇过程中,驱动减摇鳍所消耗船舶主机的能量也相对较大。因此有必要对这部分损失能量进行计算。减摇鳍在系统驱动力作用下绕鳍轴转动,可近似看作是定轴转动,近似做功[10-11]:
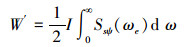 |
式中:I为减摇鳍绕鳍轴的转动惯量,Ssψ(ωe)为鳍角速率幅值谱密度。
船舶通常有一对减摇鳍,系统传动机构存在一定的传动效率,减摇鳍负载近似做功:
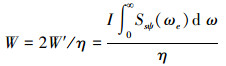 |
(3) |
式中:η为减摇鳍传动机构传动效率。
由式(3)可以看出,随着鳍角速率的增加,系统消耗的能量必定增加。因此,减摇鳍负载能量消耗作为第3个目标函数为
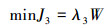 |
式中:W为减摇鳍系统近似做功,λ3为加权系数。
本文依据NJ5减摇鳍参数可以求出减摇鳍绕鳍轴转动惯量,展长为1.18 m,展弦比为0.53,弦长b=1.18/0.53=2.22 m,鳍平均厚度取0.15 m,材料密度取ρ=7.8×103 kg/m3。可近似估算鳍的重量:
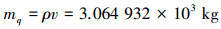 |
鳍工作时,水的附加重量取鳍质量的1/3计算,驱动系统总负载重量:
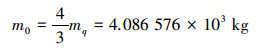 |
质量重心至鳍轴的距离R按弦长的20%估算,R=2.2×0.2=0.44 m,近似估算鳍工作时的转动惯量:
 |
再根据式(3)可求出减摇鳍负载近似做功。
综上,性能指标选取衡量横摇的横摇角方差σφ2、衡量船舶能量的鳍角方差σψ2以及减摇鳍负载能量消耗,为了保证减摇鳍系统正常工作,还需要考虑鳍角饱和率。于是得到系统要优化的多目标函数:
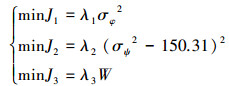 |
(4) |
以减摇鳍系统性能指标为多目标函数对PID参数KP、KI、KD进行优化整定,从而提高整体性能指标,也即转化为采用遗传算法进行多目标函数寻优问题。
3 遗传算法对多目标函数的优化要使性能指标同时达到最优,本文采用遗传算法多目标函数优化方法。因为在此类问题中,每个目标函数的优化不是独立进行的,而是要同时进行才能求出最优解。遗传算法对于求解多目标优化问题Pareto最优解常用的有5种方法[12],本文选择用权系数变换法进行系统寻优,从而将多目标优化转化为单目标优化。
对式(4)给定问题,一般很难确定一组合适的权系数。在遗传算法中有3种权系数设置的方法:固定权系数法、随机权系数法和适应性权系数法[13]。固定权系数法是对传统算法的模仿,随机权系数法和适应性权系数法,可以更全面地利用遗传算法的搜索能力。而随机权系数法采用精英保留策略以及随机权系数适应值函数,具有可变搜索方向,克服原有遗传算法容易陷入局部最优解和搜索速度慢等缺点[14]。因此文中采用随机权系数法来建立基于遗传算法的减摇鳍系统多目标优化模型。
算法实现过程:首先在式(4)中已经给每个子目标函数赋予权系数λ1、λ2、λ3,则各子目标函数的线性加权得到目标函数如式(5):
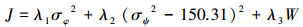 |
(5) |
式中:λ1、λ2、λ3随机权系数可以表示如式(6):
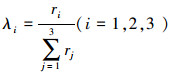 |
(6) |
式中:ri、rj为随机正整数。
在式(5)中,由于目标值之间的单位不统一,而且两者之间的数值相差很多倍,导致σφ2这个目标值没有意义。鉴于此,文中将其改进如式(7):
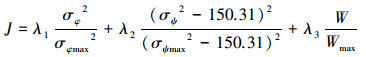 |
(7) |
式中:σφmax2、(σψmax2-150.31)2、Wmax分别是σφ2、(σψ2-150.31)2、W在第1代种群中产生的目标函数最适应值。
将式(5)改进为式(7),目标函数可以被归一化到一个稳定的水平。这样就将多目标函数转化成单目标函数优化问题,又由于采用遗传算法,适应度函数要通过比较排序计算选择概率,且适应度函数应为非负值,同时要求随着问题解提高而增加[15],鉴于上述原因,适应度函数应取式(8):
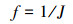 |
(8) |
其次,选出杂交个体之前,新的随机权系数由式(6)生成;接着,利用式(7)计算每个个体的适应度值。然后,根据线性比例变换函数定义方法来计算第i个个体被选择的概率pi为
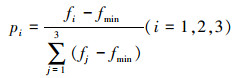 |
式中:fi、fj分别为第i和第j个个体适应度值,fmin是当前种群中最差个体的适应度值。
最后,对每一代临时存储一组最优解并按代更新[16]。本文有3个目标函数,因此Pareto解中存在3个极限点,每一个极限点可以最大化一个目标函数值。运用精华保留策略,将得到的最优解直接添加到下一代种群中[17-18]。重复以上操作直到满足系统要求。
文中减摇鳍系统控制器采用PID控制。为考虑实际应用,选择PID控制器如式(1)。使得在采用遗传算法优化PID控制作用下,系统既能满足减摇效果要求,又能满足减摇鳍能耗最小的要求。本文样本个数为50,交叉和变异概率分别为:Pc=0.8,Pm=0.01;参数KP取值为[0, 100],KI取值为[0, 50],KD取值为[0, 100],寻优时间为1 000 s,步长0.1 s。采用二进制编码,经过200代迭代。在终止种群中选出一组最优的PID控制器参数KP、KI和KD分别为11.053、0.428和32.736。
根据上面分析知基于遗传算法多目标函数优化的PID控制器原理如图 2所示。
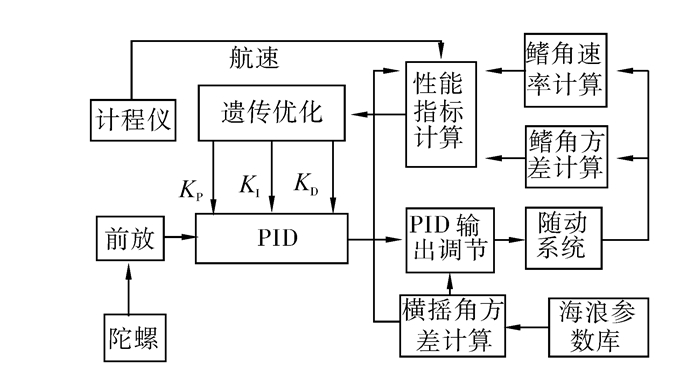
|
| 图 2 遗传算法优化控制器原理图 Fig. 2 The system scheme with optimal PID control |
传统PID控制器,在特定航速和海情下,具有良好控制效果。当船舶在海上航行时,PID参数要随海情的变化而变化。本文提出的模型,对其进行全局优化仿真。仿真海情:航速为18 Kn、22 Kn,船舶航向与海浪的遭遇角γ分别取45°、90°、135°进行仿真。图 3为无减摇装置的横摇角仿真图。减摇鳍系统对比曲线如图 4~7所示。本文传统PID控制器是在航速为18 Kn,有义波高为3.3 m,遭遇角为90°下设定,在此种海情下对减摇系统进行仿真。
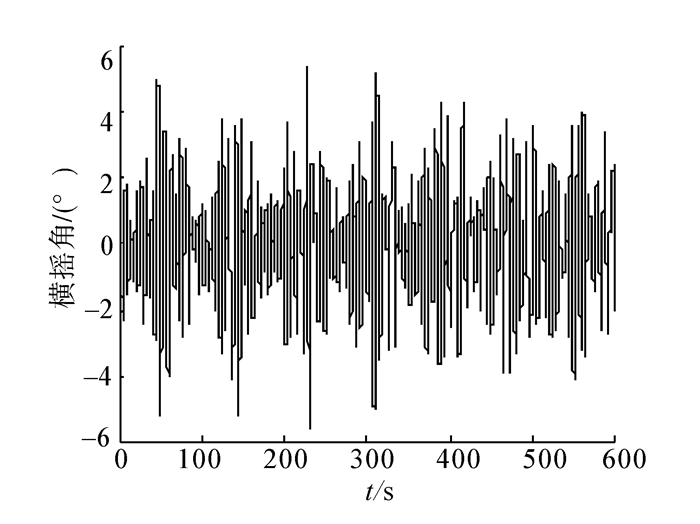
|
| 图 3 无减摇装置横摇角 Fig. 3 Roll angle without roll reduction control |

|
| 图 4 传统PID控制下横摇角 Fig. 4 Roll angle with traditional PID control |
同等仿真条件下,仿真数据对比如表 1所示。
| 航速Kn/ 遭遇角(°) |
传统PID控制 | 遗传算法优化控制 | |||||
| 横摇 角度/(°) |
鳍角 速率/(°) ·s-1 |
减摇 效率/% |
横摇 角度/(°) |
鳍角 速率/(°) ·s-1 |
减摇 效率/% |
||
| 18/45 | 0.49 | 5.3 | 75.23 | 0.47 | 4.1 | 76.35 | |
| 18/90 | 0.38 | 5.07 | 76.24 | 0.39 | 3.8 | 75.92 | |
| 18/135 | 0.36 | 4.7 | 77.33 | 0.35 | 3.2 | 79.58 | |
| 22/45 | 0.35 | 3.2 | 78.26 | 0.33 | 2.9 | 80.38 | |
| 22/90 | 0.32 | 2.4 | 79.13 | 0.31 | 2.5 | 82.96 | |
| 22/135 | 0.28 | 2.6 | 80.39 | 0.25 | 2.2 | 84.43 | |
对比图 4和图 5以及数据统计表 1可以看出,由于传统PID控制器参数是在特定航速和海情下进行设定的,所以采用遗传算法优化PID减摇效果比传统PID减摇效果稍微有所下降。但从能量消耗方面,对比图 6和图 7可以看出,采用传统PID控制的鳍角速率要大于遗传算法优化PID控制的鳍角速率,由式(3)可知,转鳍角速率大意味着减摇鳍系统工作消耗能量多。从表 1可以看出,在未设定航速和海情下,采用遗传算法优化PID控制系统在满足减摇效果基础上,能量也得到优化。说明采用遗传算法多目标优化PID控制具有可行性。遗传算法优化PID控制器不仅能提高减摇效果,而且兼顾能量最优原则。
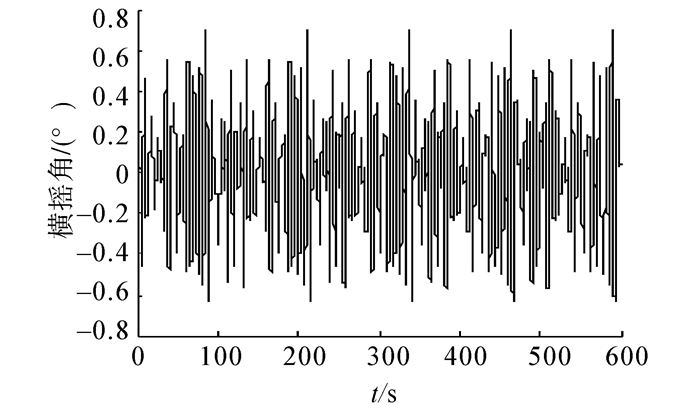
|
| 图 5 遗传算法优化PID横摇角 Fig. 5 Roll angle with optimal PID control by GA |

|
| 图 6 传统PID控制下鳍角速率 Fig. 6 Fin angular rate with traditional PID control |
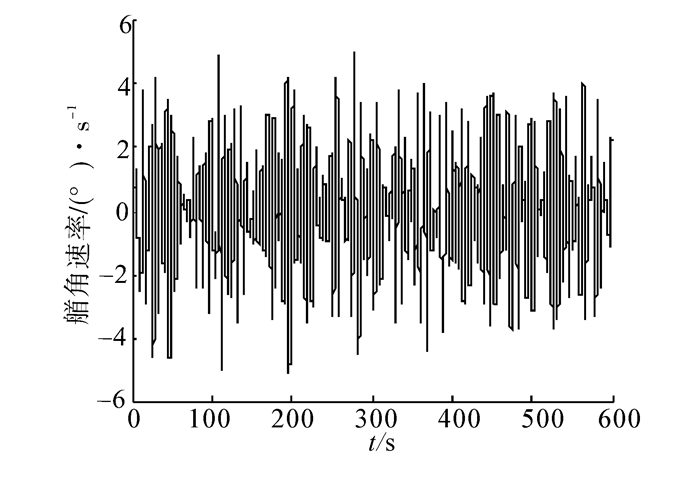
|
| 图 7 遗传算法优化PID鳍角速率 Fig. 7 Fin angular rate with optimal PID control by GA |
本文从减摇鳍能耗和减摇效果角度出发,首先对系统框图主要部分进行分析,通过横摇角方差、鳍角方差以及鳍角速率和负载能耗三方面建立性能指标。指标将能量优化与减摇效果相结合,建立多目标函数,提出采用遗传算法多目标优化方法从性能指标优化角度来探索PID控制系统优化参数,从而使能量和减摇效果得到优化。通过仿真验证减摇系统在设定航速和遭遇角情况下,采用遗传算法多目标优化方法与传统PID控制系统相比,减摇效果稍微有所下降,但能量得到优化,整体性能指标最优。在未设定航速和遭遇角情况下,采用遗传算法多目标优化方法既可以满足减摇效果,又能使减摇鳍系统能量得到优化。综上,采用遗传算法多目标函数优化方法可以很好地达到减摇和能量优化的目的,因此具有一定实际应用价值。
| [1] | 于立君, 孟祥振, 金鸿章, 等. 综合减摇系统参数配置研究[J]. 中国造船 , 2012, 53 : 13-21 YU Lijun, MENG Xiangzhen, JIN Hongzhang, et al. Study of configuration parameters of integrated stabilization system[J]. Shipbuilding of China , 2012, 53 : 13-21 |
| [2] | 修智宏, 任光. 船舶减摇鳍模糊控制器的系统化设计与仿真[J]. 系统仿真学报 , 2004, 16 (4) : 621-624 XIU Zhihong, REN Guang. Systematic design and simulation of ship fin stabilizer fuzzy controllers[J]. Acta Simulata Sys-tematica Sinica , 2004, 16 (4) : 621-624 |
| [3] | WANG F, JIN H Z, QI Z G. Modeling for active fin stabiliz-er at zero speed[J]. Ocean Engineering , 2009, 36 : 1425-1437 DOI:10.1016/j.oceaneng.2009.07.013 |
| [4] | 郭惜久, 程翔. 随机海浪模型仿真[J]. 四川兵工学报 , 2010, 31 (8) : 134-136 GUO Xijiu, CHENG Xiang. Simulation of random wave mod-el[J]. Journal of Sichuan Ordnance , 2010, 31 (8) : 134-136 |
| [5] | 金鸿章, 赵为平, 綦志刚, 等. 基于遗传算法的减摇鳍-被动水舱综合平衡系统最优控制器研究[J]. 中国航海 , 2004, 3 : 5-7 JIN Hongzhang, ZHAO Weiping, QI Zhigang, et al. Re-search on the optimized controller of fin stablilizer-passive ant-irolling tank integrated balance system based on genetic algorithm[J]. Navigation of China , 2004, 3 : 5-7 |
| [6] | NIELSEN S, ZHOU Q, KRAMER M M, et al. Optimal con-trol of nonlinear wave energy point converters[J]. Ocean En-gineering , 2013, 72 : 17-19 |
| [7] | 赵淑香.零航速下减摇鳍的运动规律与能量优化探究[D].哈尔滨:哈尔滨工程大学,2009: 34-47. ZHAO Shuxiang. Study on movement and energy optimization of zero-speed[D]. Harbin: Harbin Engineering University,2009: 34-47. |
| [8] | 宋吉广, 金鸿章, 孟令卫. 全航速减摇鳍鳍型优化设计[J]. 中国造船 , 2013, 54 (2) : 1-10 SONG Jiguang, JIN Hongzhang, MENG Lingwei. Optimum design of aerofoil for fin stabilizer at whole speed range[J]. Shipbuilding of China , 2013, 54 (2) : 1-10 |
| [9] | 马磊, 张显库. 基于混沌分析的船舶参数激励横摇运动及其减摇鳍控制研究[J]. 船舶力学 , 2013, 17 (7) : 741-746 MA Lei, ZHANG Xianku. Ship parametric excitation rolling motion and its fin stabilizer control based on chaos analysis[J]. Journal of Ship Mechanics , 2013, 17 (7) : 741-746 |
| [10] | 金鸿章, 王帆. 零航速仿生减摇鳍水动力模型改进[J]. 机械工程学报 , 2010, 46 (23) : 89-92 JIN Hongzhang, WANG Fan. Improving hydrodynamic model for zero speed bionic fin stabilizer[J]. Journal of Mechanical Engineering , 2010, 46 (23) : 89-92 DOI:10.3901/JME.2010.23.089 |
| [11] | KO C, WANGA Shufan. Precast production scheduling u-sing multi-objective genetic algorithms[J]. Expert Systems with Applications , 2011, 38 (7) : 8293-8302 DOI:10.1016/j.eswa.2011.01.013 |
| [12] | 吴君, 张京娟. 采用遗传算法的多机自由飞行冲突解脱策略[J]. 智能系统学报 , 2013, 1 (8) : 1-5 WU Jun, ZHANG Jingjuan. Conflict resolution of multiple air-planes in free flight based on the genetic algorithm[J]. CAAI Transactions on Intelligent Systems , 2013, 1 (8) : 1-5 |
| [13] | LIN Rungchuan, MUSTAFA Y, PASUPATHY K S. Multi-objective simulation optimization using data envelopment a-nalysis and genetic algorithm: specific application to deter-mining optimal resource levels in surgical services[J]. O-mega , 2013, 41 (5) : 881-892 |
| [14] | AZAMATHULLAA H, WUB F C, GHANIA A A, et al. Comparison between genetic algorithm and linear program-ming approach for real time operation[J]. Journal of Hydro-environment Research , 2008, 2 (3) : 172-181 DOI:10.1016/j.jher.2008.10.001 |
| [15] | 王健, 谢伟, 熊治国. 基于多目标遗传算法的飞行甲板参数化设计优化方法[J]. 中国舰船研究 , 2013, 8 (1) : 7-12 WANG Jian, XIE Wei, XIONG Zhiguo. Parametric optimi-zation of the flight deck design based on the multi-objective genetic algorithm[J]. Chinese Journal of Ship Research , 2013, 8 (1) : 7-12 |
| [16] | WHITTAKER G, CONFESOR J R R, GRIFFITH S M, et al. A hybrid genetic algorithm for multiobjective problems with activity analysis based local search[J]. European Journal of Operational Research , 2009, 193 (1) : 195-203 DOI:10.1016/j.ejor.2007.10.050 |
| [17] | 杨路春, 李学斌, 丁明君, 等. 多目标遗传算法和决策在船型论证中的应用[J]. 哈尔滨工程大学学报 , 2012, 33 (12) : 1459-1464 YANG Luchun, LI Xuebin, DING Mingjun, et al. Applica-tion of multi-objective genetic algorithm and decision-mak-ing skills in ship form evaluation[J]. ,Journal of Harbin Engineering University , 2012, 33 (12) : 1459-1464 |
| [18] | 李瑞敏, 陆化普. 基于遗传算法的交通信号控制多目标优化[J]. 长安大学学报 , 2009 (3) : 85-88 LI Ruimin, LU Huapu. Traffic signal control multi-object optimization based on genetic algorithm[J]. Journal of Chang'an University , 2009 (3) : 85-88 |



