2. 哈尔滨工程大学 自动化学院,黑龙江 哈尔滨 150001;
3. 哈尔滨工程大学 机电工程学院,黑龙江 哈尔滨 150001
2. College of Automation, Harbin Engineering University, Harbin 150001, China ;
3. College of Mechanical and Electrical Engineering, Harbin Engineering University, Harbin 150001, China
近年来,无人水下航行器(UUV)在海洋勘探与开发、海洋环境构建、近海污染检测等诸多领域发挥着重要作用。但由于UUV任务的复杂程度逐渐提高,对UUV控制系统的精度要求也随之提高。在复杂的海洋干扰环境下,UUV系统的非线性特性与参数的不确定性为UUV控制系统设计问题带来了很大的挑战。因此,如何使得UUV系统在复杂环境下取得更好的鲁棒性也成为了控制领域的研究热点问题。
针对一般的模型精度低,不确定干扰强的系统,传统的积分变结构控制方法具有很好的适应性与鲁棒性。但在对于如UUV等强耦合的、多状态变量的控制系统,积分变结构控制方法难以高效、快速地配置极点位置[1]。针对上述问题,本文将积分变结构控制与可拓控制理论相结合,针对UUV近水面深度控制,设计了一种可拓积分变结构控制器。可拓控制理论在物元分析理论的基础上发展而来[2],利用可拓集合的概念,以状态反馈信息的关联度作为控制器在不同测度模式的切换变量[3],使得控制器可以根据系统状态与控制需求进行更为简单、快速地参数调整,从而避免了复杂的极点配置过程,并结合了积分变结构控制的优点,增强了系统的鲁棒性。
强时变、难预测的海浪干扰为体积小、灵活性强的UUV带来了更大的挑战,针对UUV在海浪干扰下的运动控制、路径跟踪、航位推算以及故障诊断等方面的研究成为了UUV研究的热点问题[4-6]。
本文通过分析UUV海试数据,主要研究了海浪干扰下UUV近水面航行时的深度控制问题,在UUV近水面运动时,海浪所引起UUV深度传感器反馈值的波动导致了UUV深度控制指令与实际深度之间的偏差发生剧烈变化,从而导致了UUV水平舵的频繁抖动,这就严重地减少了舵机的使用寿命,而且在UUV不断进行深度控制的同时造成了不必要的能源消耗。此外,纵倾角的频繁变化也导致了导航精度的降低。为了排除海浪干扰对于UUV控制的影响,海浪的观测与估计方法也赢得了人们的重视。文献[7]提出了一种基于RMMS的海浪频域估计方法,采用数据后处理的方式得到了UUV航行区域的海浪信息。W.H.Chen等[8]提出了一种独立于控制器设计的干扰观测器设计方法,胡慧等[9]基于神经网络干扰观测器设计了针对一类不确定非线性MIMO系统的H∞跟踪控制,尹正男等[10]对干扰观测器的鲁棒优化设计方法进行了一定的研究。本文在上述研究的基础上,结合了UUV深度控制的实际情况,即海浪干扰主要体现在输出方程中,提出了一种输出干扰观测器,估计海浪带来的干扰,并利用李亚普诺夫理论证明了其收敛性。文章最后利用UUV深度控制仿真系统,结合所设计的控制器与观测器,验证本文所提出的方法的有效性与工程实际意义。
1 UUV模型与海浪模型 1.1 UUV模型根据刚体运动和流体力学原理,可以得到UUV运动的六自由度动力学模型[11]。在本文中,由于UUV的欠驱动特性,深度控制的实质均为纵倾控制,并忽略纵向控制与其的耦合,所以仅需考虑UUV纵倾控制方程,并结合运动学模型,可得到如式(1)所示的UUV深度控制的非线性数学模型。
 |
(1) |
式中:u为系统的控制输入,即为UUV水平舵舵角值。x=[θ q ζ]T为UUV系统状态,分别为纵倾角、纵倾角速度以及深度。y(t)=Z为系统的输出,为UUV的实际深度值。d(t)为系统外界干扰,即为海浪对于深度传感器的影响。在本例中,h(x)=[0 0 1],d(x)=1。
在设计积分变结构控制器时,需要对模型进行进一步的线性化处理,引入积分变量ζI、深度偏差ζe、深度指令ζr,并可以得:
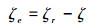 |
(2) |
 |
(3) |
根据式(2)、(3),并结合某型UUV的水动力参数, 即可得到UUV深度控制线性系统状态方程:
 |
(4) |
式中: 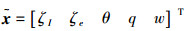
 |
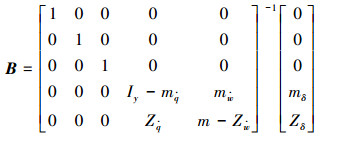 |
式中:Iy为惯性系数,ZG、ZB为重心、浮心在运动坐标系下z轴的坐标,mq、mw、mq·、mw·、Zq、Zw、Zq·、Zw·为相应的水动力系数。
1.2 海浪模型式(1)中提到的外界干扰d(t)可由式(5)所表示的海浪数学模型得到[12]。
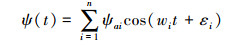 |
(5) |
在一般的情况下,n取40~60, 本文中n取50;ψai为海浪的波幅,与海浪的频谱密度等相关,在实际中均为微小量。εi为0~2π的随机数。wi为第i次谐波的角频率。准确的干扰模型对于干扰观测器的设计十分重要,为了进一步分析海浪在系统中的影响,现将海浪干扰表示为状态空间形式,如式(6)所示。
 |
(6) |
式中:ξ为海浪的系统状态,为2n×1的矩阵,C为2n×2n的矩阵,D为1×2n,如式(7)~(9)所示。
 |
(7) |
 |
(8) |
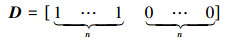 |
(9) |
基于可拓控制理论与实际UUV深度控制系统,设计了可拓UUV深度控制系统的基本结构,如图 1所示。控制系统分为决策层与执行层,分别由UUV系统中的任务控制机和运动控制机负责,本文主要研究执行层的设计问题。

|
| 图 1 UUV可拓深度控制系统框图 Fig. 1 UUV extension depth control system |
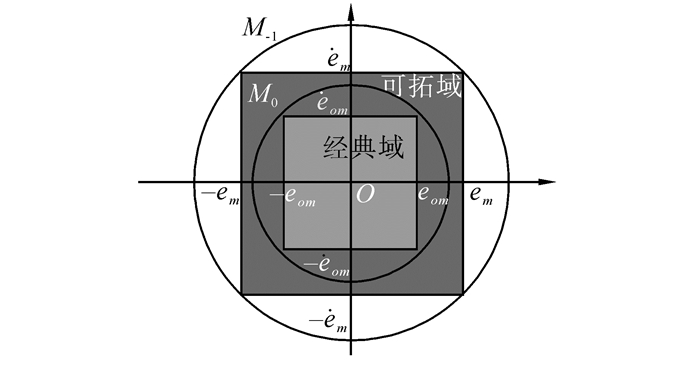
本文采用了深度偏差以及偏差的微分作为系统的控制系统状态反馈量,建立了关于这2个变量的可拓集合。设状态量偏差及其偏差导数的容许范围分别为eom和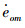


|
| 图 2 系统状态的可拓集合 Fig. 2 Extension set of UUV states |
关联度函数的表达式如下:
设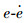
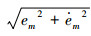



 |
(10) |
式中:Cr为图 2中所示的经典域,SS0=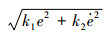
根据式(10)的形式可以看出,关联度函数所表征的是当前系统状态与可拓集合的关联程度,为测度模式的切换依据。
在本文中,通过关联度的值将系统划分为M1、M2、M3 3种测度模式,如式(11)所示。
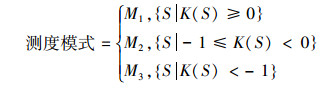 |
(11) |
根据系统当前状态所属的不同的测度模式M1、M2、M3,将系统相对应地分为经典域、可拓域和非域,在不同的测度模式下,对UUV深度控制系统的控制采用不同的控制算法。
2.2.1 经典域:测度模式M1根据由上文简化的线性系统模型(4),设计了积分变结构控制器,并且加入了饱和函数,解决了滑动控制在切换面震荡的问题。切换函数取为
 |
(12) |
根据式(4)、(12),积分变结构控制器为
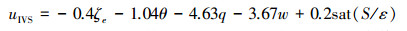 |
式中:ε为饱和函数的边界层厚度,本文中ε取常值1.8。sat(S/ε)为式(13)所示:
 |
(13) |
可拓域控制方法是可拓控制区别于其他控制方法的关键。其控制器如式(14)所示:
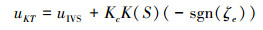 |
(14) |
式中:参数Kc根据关联度在控制中的作用进行选择。在可拓控制中,可以通过对参数k1、k2、Kc的调整来实现对系统控制性能的改善,从而使得上文所设计的积分变结构控制器参数不需要频繁地调整。
根据式(14)可知,当关联度值较小时,可拓控制与积分变结构控制间的差别不大,可拓域中的控制器对控制系统的影响不明显。在UUV深度控制系统设计中,过大的深度超调会对UUV系统安全产生严重威胁,因此要求系统具有较小的超调量或零超调。针对上述问题,本文在式(11)的基础上,加入了系统的状态偏差因子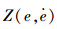
综上所述,可以得到可拓域的控制律为
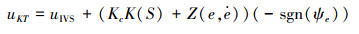 |
(15) |
式中: 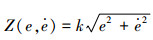
在非域中,控制器输出取最大输出值um,在本文中,即为所能达到的最大水平舵舵角。
3 输出干扰观测器设计本节利用所建立的UUV深度控制模型和海浪模型,利用线性矩阵不等式,设计了一种输出干扰观测器,并根据李亚普诺夫理论证明了其稳定性。
3.1 干扰观测器设计干扰观测器模型如式(16)所示:
 |
(16) |
式中:L(x)为系统的增益矩阵,将在后文求取。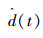
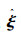
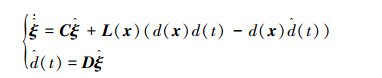 |
(17) |
不妨取L(x)=Kd-1(x),则可以得到关于海浪的状态微分方程:
 |
(18) |
上文中,得到了如式(8)所示海浪干扰观测器。设变量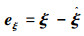
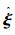

因此,取李亚普诺夫函数Vξ=eξTPeξ,其中P为正定矩阵,可知Vξ>0。对Vξ求导可得
 |
结合式(17),可得
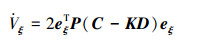 |
定义变量C=C-KD,则可得
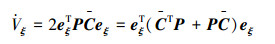 |
当CTP+P C < 0时,可得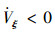
 |
利用MATLAB线性矩阵不等式工具箱即可求得P值,进一步根据K=P-1DT求取K值。
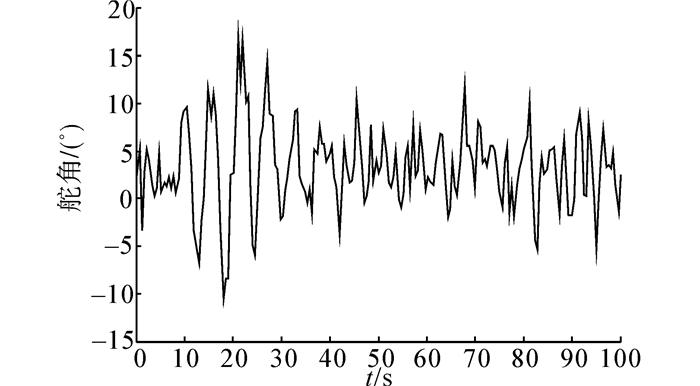
4 仿真实验与分析当UUV在近水面定深航行时,由于海浪干扰引起的深度变化会导致UUV不断地调整其深度值。当UUV为欠驱动时,就导致了UUV水平舵的不断抖动,对舵机产生不必要的磨损,同时也使得UUV纵倾不断变化,如图 3所示。在仿真实验中,UUV的深度控制指令为7 m,海浪等级为3级,采用所设计的可拓积分变结构控制器。取深度控制稳定后数据,通过图 3可以看出,实际的水平舵舵角在-10°~15°之间剧烈地抖动,其非对称性是由于UUV的正浮力所致。通过图 4可知,纵倾角主要在-3.5°~2°间波动。
|
| 图 3 定深航行舵角曲线 Fig. 3 Deflection angle for constant depth maneuvering |

|
| 图 4 定深航行纵倾曲线 Fig. 4 Pitch angle for constant depth maneuvering |
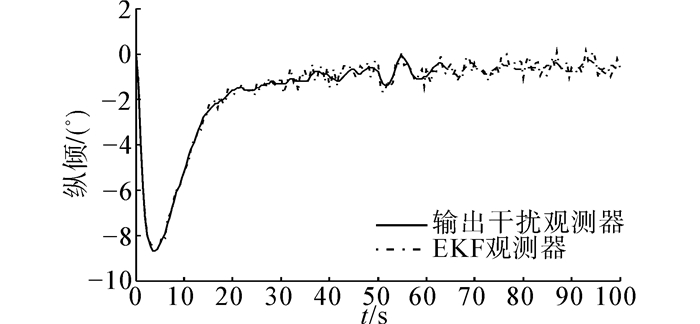
在实际近水面航行中,这种对于海浪引起的深度传感器变化的响应并没有实际意义。利用式(16)所示输出干扰观测器,估计海浪干扰值,同时,本文加入了采用EKF方法的海浪观测器进行对比,可得到如图 5、图 6所示的舵角、纵倾曲线。此时,由于系统不再响应海浪干扰,其深度反馈值并未稳定在指令深度7 m。如图 7所示。

|
| 图 5 加入观测器后舵角曲线 Fig. 5 Deflection angle with disturbance observer |
|
| 图 6 加入观测器后纵倾曲线 Fig. 6 Pitch angle with disturbance observer |

|
| 图 7 加入观测器后深度控制曲线 Fig. 7 Depth control with disturbance observer |
通过图 7所示的深度曲线可以看出,虽然深度值并未稳定在指令深度上,但其变化曲线与海浪模型基本相符,分析图 5、图 6所示的舵角曲线和纵倾曲线,仅考虑深度稳定后的曲线,即在40 s之后,虽然舵角与纵倾值仍有一定的抖动,但相比于图 3、图 4所示的曲线,其抖动在频率和幅值上均有所改善,相比于EKF方法,也得到了一定的提高。如表 1所示。通过仿真实验,证明了该方法的有效性和工程实际意义。
| 对比项 | 舵角 幅值/(°) |
舵角 频率/Hz |
纵倾 幅值/(°) |
纵倾 频率/Hz |
| 无观测时 | 15 | 0.5 | 3.5 | 0.2 |
| 加入EKF观测器 | 10 | 0.3 | 2.5 | 0.13 |
| 加入输出干扰观测器 | 5 | 0.2 | 2 | 0.1 |
5 结束语
本文针对UUV近水面深度控制问题,设计了基于可拓逻辑与积分变结构方法的可拓积分变结构控制器,充分利用了可拓理论中的信息转换的思维模式,在一定程度上弥补了积分变结构控制器极点调整复杂的缺陷,实现了对强耦合、高度非线性AUV系统的动态控制。针对UUV在近水面航行时易受海浪干扰影响的问题,将干扰观测器理论应用到了海浪干扰估计中。利用已知UUV数学模型和海浪模型,设计了输出干扰观测器,并利用李亚普诺夫理论和线性矩阵不等式方法证明了观测器的稳定性。最后,利用仿真实验,证明了所设计的控制器与观测器的有效性。
| [1] | 熊华胜, 边信黔. 积分变结构控制原理在AUV航向控制中的应用仿真[J]. 船舶工程 , 2005, 27 (5) : 30-33 XIONG Huasheng, BIAN Xinqian. Simulation of AUV heading control system using integral variable structure control principle[J]. Ship Engineering , 2005, 27 (5) : 30-33 |
| [2] | 蔡文. 物元分析[M]. 广州: 广东高等教育出版社, 1987 : 23 -26. |
| [3] | 潘东, 金以慧. 可拓控制的探索与研究[J]. 控制理论与应用 , 1996, 13 (3) : 305-311 PAN Dong, JIN Yihui. Exploration and research on extension control[J]. Control Theory and Applications , 1996, 13 (3) : 305-311 |
| [4] | MOREIRA L, SOARES C G. H2 and H∞designs for diving and course control of an autonomous underwater vehicle in presence of waves[J]. IEEE J Ocean Eng , 2008, 33 (2) : 69-88 DOI:10.1109/JOE.2008.918689 |
| [5] | LIU S, WANG D, POH E. Non-linear output feedback tracking control for AUVs in shallow wave disturbance condition[J]. Int J Control , 2008, 81 (11) : 1806-1823 DOI:10.1080/00207170801898885 |
| [6] | SANYAL A K, CHYBA M. Robust feedback tracking of autonomous underwater vehicles with disturbance rejection[C]//2009 American Control Conference. St. Louis, MO, USA, 2009: 3585-3590. |
| [7] | GOODMAN L, LEVINE E R, WANG Z K. Subsurface observations of surface waves from an autonomous underwater vehicle[J]. IEEE J Ocean Eng , 2010, 35 (4) : 779-784 DOI:10.1109/JOE.2010.2060551 |
| [8] | CHEN W H. Disturbance observer based control for nonlinear systems[J]. IEEE/ASME Trans on Mechatronics , 2004, 9 (4) : 706-710 DOI:10.1109/TMECH.2004.839034 |
| [9] | 胡慧, 刘国荣. 基于神经网络干扰观测器的一类不确定非线性MIMO系统H∞跟踪控制[J]. 控制与决策 , 2009, 24 (3) : 468-471 HU Hui, LIU Guorong. H∞ tracking control of a class of uncertain nonlinear MIMO systems based on neural network disturbance observer[J]. Control and Decision , 2009, 24 (3) : 468-471 |
| [10] | 尹正男, 苏剑波, 刘艳涛. 基于H∞范数优化的干扰观测器的鲁棒设计[J]. 自动化学报 , 2011, 37 (3) : 331-341 YIN Zhengnan, SU Jianbo, LIU Yantao. Design of disturbance observer with robust performance based on H∞norm optimization[J]. Acta Automatica Sinica , 2011, 37 (3) : 331-341 |
| [11] | 李殿璞. 船舶运动与建模[M]. 北京: 国防工业出版社, 2008 : 14 -16. |
| [12] | 金鸿章. 船舶控制原理[M]. 哈尔滨: 哈尔滨工程大学出版社, 2001 : 18 -24. |



