多智能体系统的能控性问题已引起学术界的高度重视。对该问题的研究源于自然界中普遍存在的群体行为,例如生物界昆虫、鸟和鱼群等协作捕食, 共同抵御入侵者等行为。自然界中的群体行为使得它们能很好地生存繁衍下去,同时也给人类以很大的启发:与单个智能体相比,多智能体系统的合作可以大大提高系统的性能,完成更复杂的任务。H.G.Tanner[1]最早提出了领导者-跟随者结构下多智能体系统的能控性问题。然后Rahmani等[2]介绍了多智能体能控的代数和图论的条件。随后,许多人开始从图论的角度[3-5]研究多智能体系统的能控性,并在连续时间[6]和离散时间[7]2种情形下,对多智能体系统的能控性问题分别进行了讨论。多智能体系统的能控性问题具有重要的现实意义,可以通过它研究多智能体网络的编队控制问题[9],即通过调节领航者的行动来驱动跟随者到达理想的位置,从而实现系统的能控性。随着在领导者-跟随者结构下多智能体系统的不断发展,渐渐地有人开始尝试在新的结构下研究多智能体系统的能控性问题。目前,越来越多的人开始在广播信号结构[10-11]下研究系统的能控性。然而,到目前为止,这方面的研究成果还不多。广播信号结构与领导者-跟随者结构相比有以下优势:1)在现实生活中已得到广泛应用,例如电台和电视台等;2)硬件上的优势,不需要提供用于领导者和跟随者进行信息交流的设备等。多智能体的能控性问题已取得了长足的进展,但都是在网络中的智能体都是相同(即一致动态)的假设下进行的,采用这种假设可以更容易地分析网络,特别是对网络的同步问题和能控性问题。然而,大多数实际工程中的动态网络具有不同的节点动态,例如一个动力系统具有不同的物理参数,其发电机和负载等结构通过运输线相互连接,共同构成一个非一致的动态网络。因此,研究具有非一致动态[8, 12]的多智能体网络的能控性问题,无论从理论角度还是从实践角度来说,都具有极其重要的意义和价值。本文致力于研究在广播控制信号下,具有非一致动态的非定向的多智能体网络的能控性问题,而非定向的多智能体网络是指在无向图下研究多智能体系统。
1 图论准备知识和模型 1.1 图论准备知识本文的信息交换图均为无向图,关于无向图更全面的结论可参看文献[14]。一个无向图G包含一个顶点集V(G)和一个边集E(G)。无向图中的边可以用(i, j)表示。如果(i, j)∈E(G),那么i和j是相邻关系,可以用i~j表示。令Ni表示vi的邻集,则
任何无向图都可以由它的邻接矩阵A(G)来表示,邻接矩阵能充分表达图上顶点相邻的关系,是一个只含有元素0和1的对称矩阵。如果i和j是相邻的,则aij是1,否则为0。度数矩阵D(G)是一个对角矩阵,其中aii是节点vi的度数。拉普拉斯矩阵L(G)=D(G)-A(G),也是一个对称矩阵。拉普拉斯矩阵与节点的互联拓扑有关。
1.2 模型考虑如下多智能体系统:
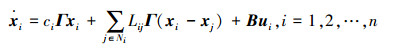 |
(1) |
式中:xi∈Rm是第i个智能体的状态,ui∈Rp是控制输入信号。因为每个节点都接受ui,所以称为广播控制信号。B∈Rm×p是该系统的控制输入矩阵。ciΓxi(ci∈R, ci≠0)描述了系统中非一致的节态。Γ∈Rm×m为表示节点分量之间内部耦合关系的常数矩阵。LijΓ(xi-xj)指的是相邻节点之间的信息交流,即所谓的邻域信息交互, 其中Lij是拉普拉斯矩阵L(G)的元素。
为了更好地分析系统能控性,可以将系统转换成紧凑的矩阵形式。令x=[x1T x2T … xnT]T∈Rm×n,u=[u1T u2T … unT]T∈Rp×n,系统(1)可以改写成:
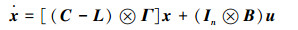 |
(2) |
式中:C=diag(c1, c2, …, cn)。
定义1 对具有如(1)动态的多智能体系统,如果对任意的初始状态,都存在一个控制输入信号使得系统在有限的时间内从该初始状态到达任意期望的状态,那么就称多智能体系统是能控的。
命题1 对于系统
1)系统是能控的。
2)系统能控性矩阵[B AB A2 B …An-1B]满秩。
3)对于所有的λ∈R,矩阵[λI-A B]满秩,即如果vTA=λvT,则vTB≠0T,其中v是A对应于特征值λ的非零左特征向量(PBH判据)。
命题2 矩阵的Kronecker积有以下性质[16]:
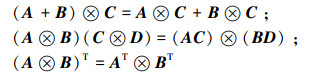 |
4)设A∈Cm×m的全体特征值为λ1, λ2, …, λm,其相应的特征向量α1, α2, …, αm,B∈Cn×n的全体特征值为μ1, μ2, …, μn,其相应的特征向量是β1, β2, …, βn,那么,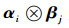
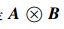
定义2 如果当|i-j|≤1时, Jij > 0,而当|i-j|≥2时,Jij=0,称J是雅可比矩阵[13],表示成矩阵形式为
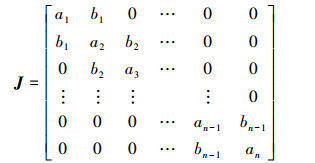 |
式中:ai, bi > 0。在这里,只介绍下文用到的雅可比矩阵的一个性质:雅可比矩阵的特征值各不相同。
2 能控性分析 2.1 主要结果定理1 设Γ是对称的,则具有如式(1)动态的多智能体系统能控当且仅当下面的2个条件同时成立:
1)[Γ, B]是能控矩阵对;
2) 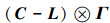
证明系统的能控性矩阵为
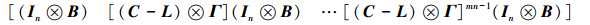 |
因为C是对角矩阵,拉普拉斯L是对称矩阵,所以C-L是对称矩阵。在Γ是对称矩阵的条件下,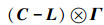
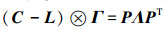

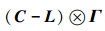
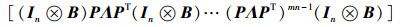 |
简化为
 |
将P提出,能控性矩阵可以写成:
 |
因为P非奇异,所以P不影响能控性矩阵的秩。因此,仅研究下述矩阵的秩即可。
 |
要使该矩阵行满秩,
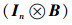
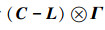


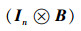
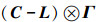
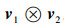



 |
因此,系统能控,当且仅当:
1)v1TIn≠0T,即没有一个C-L的特征向量正交于In,也就是说,C-L的特征向量不为0n。因为特征向量的定义是非零向量,所以这个条件在任何情况下均成立,所以可以不考虑该条件。
2)v2TB≠0T,即没有一个Γ的特征向量正交于B,根据命题1的陈述(3),[Γ B]是一个控制矩阵对。
由于Λ是一个对角非奇异矩阵,故Λ乘以一个矩阵只会使该矩阵的各个元素得到相同比例的缩放。然而,矩阵Λ对角线上的元素不能出现相同的元素,否则,能控性矩阵会出现线性相关的行,则控制矩阵也不能行满秩。因为矩阵Λ是一个对角矩阵,且其主对角线元素为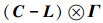
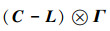
综上所述:当Γ是对称的,欲使系统(2)能控,当且仅当下面的2个条件同时成立:
1)[Γ B]是能控矩阵对;
2) 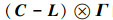
根据定理1,广播信号下非一致多智能体系统的能控性问题可以分解成2个独立的小问题:1)子系统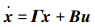


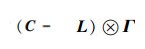
首先,研究定理1的条件1),即子系统
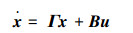 |
(3) |
的能控性。其中Γ∈Rm×m,B∈Rm×p的定义同(1)。
定理2 Γ是对称的(同定理1),则系统(3)能控当且仅当下述2个条件同时成立:
1)Γ的特征值各不相同;
2)Γ的特征向量不正交于B。
证明:系统(3)的能控性矩阵是
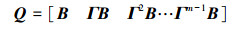 |
因为Γ对称,所以它可以表达为Γ=UDUT,其中D是一个对角矩阵,其主对角线元素为Γ的特征值,而相似变换矩阵U的列向量是对应于Γ的特征值的正交特征向量[16]。那么,矩阵Q可以改写成:
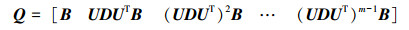 |
可以简化为
 |
将U提出,矩阵Q可以转换成:
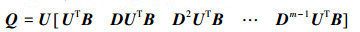 |
因为矩阵U非奇异,所以U不影响Q的秩。因此,主要研究式(4)矩阵的秩即可。
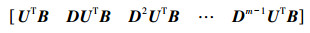 |
(4) |
欲使Q行满秩,UTB的行向量应是非零的,也就是说,不存在U的列向量,其与B的所有列向量正交。否则将会出现式(4)矩阵的一整行元素均是零的情况,那么式(4)就不是行满秩的,即Q不是行满秩的。因为相似变换矩阵U的列向量是对应于Γ的特征值的正交特征向量,所以U的列向量不能正交于B,也就是说,Γ的特征向量不正交于B。由于D是一个对角非奇异矩阵,故D乘以一个矩阵只会使该矩阵的各个元素得到相同比例的缩放。然而,D对角线上的元素不能出现相同的元素,否则,Q会出现线性相关的行,则控制矩阵Q也不能行满秩。因为D是一个对角矩阵,其主对角线元素为Γ的特征值,所以要求Γ的特征值各不相同。
综上所述:当Γ是对称的,系统(3)可控,当且仅当下述2个条件同时成立:
1) Γ的特征值各不相同;
2) Γ的特征向量不正交于B。
2.3 路和完备图的能控性为了更全面理解系统能控性,本小节针对多智能体系统信息交换拓扑中的2类特殊构形路和完备图讨论
对具一致动态的多智能体系统而言,当信息交换拓扑结构为路PN时,系统可控[1, 3, 8]。下面的研究表明,对非一致的多智能体系统,情况发生变化,路既可能可控,也可能不可控。原因如下:
无向图路的拉普拉斯矩阵为
 |
那么,具有非一致动态路径的拉普拉斯矩阵为
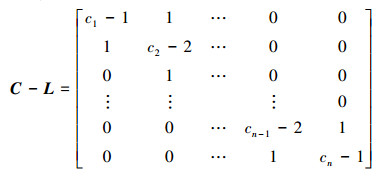 |
根据定义2可知,矩阵C-L是一个雅可比矩阵,而雅可比矩阵的特征值各不相同的。那么,在子系统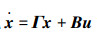

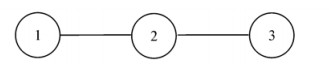
例1 图 1是一个简单的三节点的路径,特殊的是各节点的状态不同(即非一致动态),且每个节点都接受控制输入信号(即广播信号)。
|
| 图 1 三节点的路径 Fig. 1 The path of three nodes |
该例子是在子系统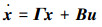
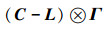
1)设

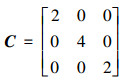
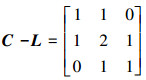

2)设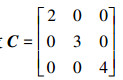



综合1)、2)可得:非一致多智能体系统中,若其信息交换图为路,系统既可能可控,也可能不可控。
已有结果表明,对具一致动态的多智能体系统来说,完备图KN不可控[1, 3, 8]。由例2知,当多智能体系统的动态是非一致时,完备图既可能可控,也可能不可控。
例2 图 2是一个四节点的完备图,特殊的是各节点的状态不同(即非一致动态),且每个节点都接受控制输入信号(即广播信号)。
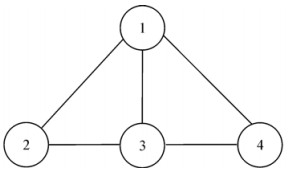
|
| 图 2 四节点的完备图 Fig. 2 The complete graph of four nodes |
该例子是在子系统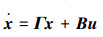
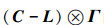
1)令对称阵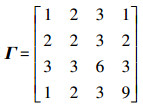
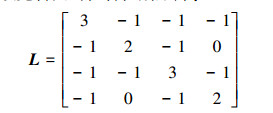 |
设


2)设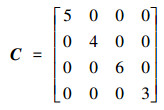

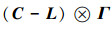
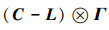
综合(1)、(2)可得:非一致的多智能体系统中的完备图,既可能可控,也可能不可控。
上述讨论表明,具非一致动态的多智能体系统其能控性比一致动态的多智能体系统更加复杂,其特殊构形的能控性结论通常发生改变。
2.4 改善方法根据定理1,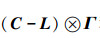
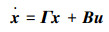
1)改变节点的非一致动态,即各节点参数ci。例如:例1、例2的(1)、(2),通过改变节点参数使得路和完备图由不能控变为能控。
2)改变多智能体系统的拓扑结构。例如:可以通过增加或去掉节点间的联系,将不能控的拓扑结构转换成接近的能控的拓扑结构。
3 结束语本文在广播信号下,对非一致的多智能体系统的能控性进行了研究,得到了使其能控的充分必要条件,并进一步分析证明了该充分必要条件。为了得到更深入的理解,在非一致动态下还研究了路径和完备图的能控性,研究结果表明,与一致动态的多智能体系统相比,非一致情形在广播信号下,路和完备图的能控性发生变化,并指出节点的非一致动态使多智能体系统的能控性问题更加复杂。此外,还提出了改善非一致多智能体系统能控性的方法。与领导者-跟随者结构相比,广播信号结构在现实生活中(如电台和电视台)更为普遍,本文研究的非一致动态与实际工程中的动态网络更为接近,无论从理论还是实践角度,本文的研究都有其自身的价值和意义。
| [1] | TANNER H G. On the controllability of nearest neighbor interconnections[C]//Proceedings of the 43rd IEEE Conference on Decision and Control. Atlantis Paradise Island, Bahamas, 2004: 2467-2472. |
| [2] | RAHMANI A, MESBAHI M. On the controlled agreement problem[C]//Proceedings of the IEEE American Control Conference. Minneapolis, USA, 2006: 1376-1381. |
| [3] | RAHMANI A, JI Meng, MESBAHI M, et al. Controllability of multi-agent systems from a graph-theoretic perspective[J]. SIAM Journal on Control and Optimization , 2009, 48 (1) : 162-186 DOI:10.1137/060674909 |
| [4] | JI Meng, EGERSTEDT M. A graph-theoretic characterization of controllability for multi-agent systems[C]//Pro-ceedings of the IEEE American Control Conference. NewYork, USA, 2007: 4588-4593. |
| [5] | QI Xiao. On controllability of linear systems from a graph-theoretic perspective[C]//Proceedings of the 31st Chinese Control Conference. Hefei, China, 2012: 152-154. |
| [6] | LIU Bo, XIE Guangming, CHU T, et al. Controllability of interconnected systems via switching networks with a leader[C]//IEEE International Conference on Systems, Man and Cybernetics. Taipei, China, 2006: 3912-3916. |
| [7] | LIU Bo, CHU T, WANG L, et al. Controllability of a leader-follower dynamic network with switching topology[J]. IEEE Transactions on Automatic Control , 2008, 53 (4) : 1009-1013 DOI:10.1109/TAC.2008.919548 |
| [8] | XIANG L Y, ZHU J H, CHEN Fei, et al. Controllability of weighted and directed networks with nonidentical node dynamics[OL/EB]. [2014-01-20].[http://www.hindawi.com/journals/mpe/2013/405034/]. |
| [9] | JI Z J, WANG Z D, LIN H, et al. Interconnection topologies for multi-agent coordination under leader-follower framework[J]. Automatica , 2009, 45 (12) : 2857-2863 DOI:10.1016/j.automatica.2009.09.002 |
| [10] | AZUMA S, YOSHIMURA R, SUGIE T. Broadcast control of multi-agent systems[J]. Automatica , 2013, 49 (8) : 2307-2316 DOI:10.1016/j.automatica.2013.04.022 |
| [11] | YOON M G, ROWLINSON P, CVETKOVIC D, et al. Controllability of multi-agent dynamical systems with a broadcasting control signal[J]. Asian Journal of Control , 2014, 16 (4) : 1-7 |
| [12] | COWAN N J, CHASTAIN E J, VILHENA D A, et al. Nodal dynamics, not degree distributions, determine the structural controllability of complex networks[J]. PLoS ONE , 2012, 7 (6) -e38398 |
| [13] | BLOEMENDAL A. Jacobi matrices[EB/OL]. [2012-05-30]. [DOI:http://www.math.harvard.edu/~alexb/rm/Jacobi.pdf]. |
| [14] | GODSIL C, ROYLE G. Algebraic Graph Theory[M]. New York: Springer, 2001 : 1 -295. |
| [15] | CHEN C T. Linear system theory and design[M]. New York: Oxford University, 1999 : 144 -153. |
| [16] | 徐仲, 张凯院, 陆全, 等. 矩阵论简明教程[M]. 北京: 科学出版社, 2001 : 5 -164. |



