传统模式识别主要针对测试模式为单观测样本的情况。然而,随着人工智能技术的飞速发展,数据采集工作变得越来越容易,人们常常可以获取某特定模式在不同时刻或不同条件下的多个观测样本。例如,日常生活中,可以用摄像头获取一个物体或一个人在不同时刻、不同光照条件下的图像数据,也可以借用多个摄像头从不同的角度获取图像数据。此外,即使是相同的观测数据,若用不同的方法进行数据转换,得到的特征值也不一样,这些就构成了同一模式的多观测样本。多观测样本相对于单观测样本能提供更多关于测试模式的信息,从而提高分类精度[1]。由此可以预见,多观测样本分类问题将得到国内外研究学者的广泛关注。
目前,多观测样本的分类方法主要有2类:一类是基于参数模型的方法。例如,文献[2]提出了基于概率密度的KLD(KL-divergence),该方法把所有样本集看作是独立的,并且服从高斯分布,然后通过计算测试样本集和各个训练样本集间的KL散度来确定多观测样本的类别。但是此方法仅仅对那些服从单高斯分布的样本集比较适用,难以精确地描述数据呈非线性分布的情况。针对这一情况,O.Arandjelovic等[3]提出了半参数混合高斯模型,并将其应用在KL散度的计算中,从而解决了非线性分布的多观测样本分类问题。然而,此方法的计算复杂度相对较大。F.Cardinaux等[4]通过嵌入局部特征来扩展GMM(Gaussian mixture model),在保证低复杂度的同时进一步提高了分类性能。文献[5]提出了一种基于核函数的分类方法,该方法利用信息论的相关知识,把RAD(resistor-average distance)看作是多观测样本间的相似度来完成多观测样本的分类。以上这些方法的不足在于它们不但要解决复杂的参数估计问题,而且当多观测样本和测试样本集之间的统计相关性较弱时,它们的性能会有大的波动。另一类是基于非参数模型的方法,其中最具代表性的是基于子空间的方法,此类方法把子空间的相似度作为多观测样的分类依据,例如,文[6]提出的MSM (mutual subspace method),首先用PCA特征子空间来表示每一类的训练样本集和多观测样本,再利用子空间之间的主成分角作为相似性度量,最后用子空间的典型相关性(canonical correlation)来实现多观测样本的分类,但该算法对数据的变化较为敏感。为此,K.Fukui等[7]又提出CMSM(constraint mutual subspace method)来消除MSM的数据敏感性,将原空间的所有样本集都映射到同一约束子空间,在此约束空间中计算样本集间的主成分角,再用子空间的典型相关性完成多观测样本的分类。但上述2种方法并没有考虑到数据的非线性分布问题,针对这一问题,H.Sakano等[8]提出KMSM(kernel mutual subspace method)算法,L.Wolf等[9]提出KPA(kernel principal angles)算法,使用核函数来解决数据的非线性问题,进而完成多观测样本的分类。虽然KMSM和KPA考虑了数据的非线性分布,但是这2种方法用到的核函数对参数的依赖性较大。以上这些方法都没有考虑到通过转换数据可以提取到更多的判别信息,T.K.Kim等[10]提出DCC(discriminant canonical correlation)算法,其首先通过训练获得一个能使类内典型相关性最大而类间典型相关性最小的判别转换矩阵,然后把原空间数据映射到新的子空间上,在此基础上把典型差分相关性作为相似度量进行分类,此方法存在未考虑数据非线性分布的缺点。一些研究者曾认为所有典型相关性对分类的贡献是相同的,即权值相等。但后来T.K.Kim等[11]发现在分类中不同的典型相关性所起的作用是不同的,继而提出了BoMPA(boosted manifold principal angles)算法,该算法首先通过PPCA(probabilistic PCA)搜索局部线性模块,并将得到的所有模块表示成PCA子空间的形式,进而计算子空间之间的典型相关性,然后把训练集表示为正负样本特征的形式,同时采用AdaBoost算法得到相应的权值,最后用加权后的主成分角来度量子空间的相似性,实现多观测样本的分类。在此基础上,X.Li等[12]提出Boosted全局和局部主成分角联合的分类算法。文献[13]提出MMD (manifold-manifold distance)方法,该方法将典型相关性和局部线性模块结合起来,首先用联合局部线性模型的集合来表示子空间所描述的流形,从而把MMD转换为线性模块的组合,最终通过MMD的计算来对观测样本进行分类,但该方法的计算量和复杂度相对较大。W.S.Chu [14]提出KDT(kernel discriminant transformation)来解决多观测样本的分类问题,该方法用核子空间来表示每个样本集,同时定义一个能使类内核子空间相似性最大而类间核子空间相似性最小的KDT矩阵,从而把多观测样本的分类问题转换为寻求KDT矩阵的最优解问题。近来,E.Kokiopoulou等[15]在标记传播算法的基础上提出了MASC(mAniflod-based smoothing under constrain)算法,该算法将k-近邻图运用到多观测样本的分类问题中,但是k-近邻图的边权值的计算采用了欧式距离下的高斯核函数,而基于欧式距离的测度无法全面反映数据的空间分布特性。
由上述可知,目前的多观测样本分类算法都有一定的不足和局限性。本文在经典SVM算法的基础上,用SVM的相关理论来实现多观测样本的分类。与传统的SVM算法相同,本文方法适用于小样本情况,利用核函数解决了非线性问题和维数问题,其算法复杂度与样本维数无关。然而,与传统分类方法的不同在于,该方法无需对分类器进行训练或提前对训练集进行特征表示,而是将测试集和训练集作为一个整体,充分利用特征空间中同类样本连续分布这一特点,使得分类更加准确。
1 多观测样本二分类问题的描述多观测样本形成示意图如图 1所示。在多观测样本的二分类问题中,若假设测试模式为s,则该问题就是将测试模式的多观测样本确定为2种类别中的一类。

|
| 图 1 多观测样本形成示意图 Fig. 1 Schematic diagram of producing multiple observations |
假定测试模式s的多测样本为
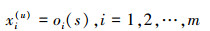 |
(1) |
式中:上标(u)表示各个观测样本是未标记的,m表示观测样本的数目,oi(s)表示模式s的第i个单观测样本,它可能是模式s经过平移、旋转、缩放或者是透视投影得到的,也可能是模式s在某一特定时刻的观察记录。
多观测样本二分类问题的数据集可表示为X={X(l), X(u)},其中X(l)={x1, x2, …, xl}⊂Rd,d为样本维数,X(l)表示已知标签的样本集,含有l个样本,X(l)涵盖了所有类别的数据。X(u)={xl+1, xl+2, …, xn}⊂Rd, n=l+m,X(u)表示未知标签的样本集,含有m个样本,并且所有样本属于同一类别,其对应于式(1)的多观测样本,即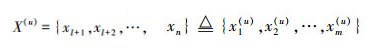
综上所述,多观测样本二分类问题可正式定义为:给定已知标签的样本集X(l)和未知标签的样本集X(u),而X(u)对应于模式s的多观测样本,即
支持向量机(support vector machine, SVM)是一种基于结构风险最小化(structural risk minimization,SRM)原理,在统计学习理论的基础上发展起来的机器学习方法[16]。SVM的基本实现方法就是在原空间或者经过投影后的高维空间中构造最优分类面,并将此分类面作为分类决策面进行数据分类。
SVM最基本的理论是用来解决二分类问题的,SVM的目标就是构造线性最优分类超平面,使其将2类样本完全正确地分开,同时使分类间隔最大。对于给定的样本集,(xi, yi), i=1, 2, …, l, xi∈Rd, yi=±1,当样本集线性可分时,对应的线性判别函数的一般形式为:g(x)=(wTx)+b,其中w、b为n维向量,对判别函数作归一化处理,使离分类面最近的样本满足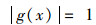
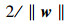

 |
(2) |
且使
综上所述,最优分类面的求解问题等价于在式(2)的约束下最小化式(3):
 |
(3) |
而这一问题可以通过定义拉格朗日函数(式(4))来求解:
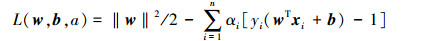 |
(4) |
式中:αi≥0为Lagrange系数,则问题转换成对w和b求Lagrange函数的最小值。式(4)分别对w、b求偏微分,并令结果为零,则有
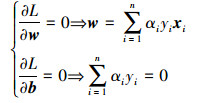 |
(5) |
将式(5)代入式(4),则原问题可以进一步转化为凸二次规划的对偶问题:
 |
(6) |
在式(6)所得的结果中,只有少数的αi不等于零,其对应的样本离最优分类面最近,这些样本被称为支持向量。上述问题存在惟一最优解,若最优解为αi*, 则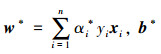
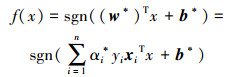 |
对于样本集非线性可分的情况,可以先把原始空间的样本集通过非线性变换φ映射到一个高维的特征空间,使得样本集在新的空间线性可分,然后构造最优分类平面。这种非线性变换可以通过引入适当的核函数来实现,用k(xi, xj)=φ(xi)·φ(xj)代替线性可分情况下的点积(xiT, xj),式(6)中的优化函数变为
 |
最终的分类函数为
 |
在线性不可分的问题中,SVM还引入了惩罚因子C和松弛变量ξ,此时最优分类面的求解问题可描述为
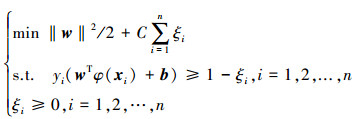 |
同样地,通过定义拉格朗日函数的方法可以将原问题转换为凸二次规划的对偶问题:
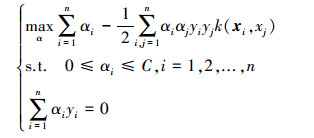 |
对应的最优分类函数为
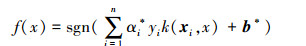 |
由于支持向量机具有结构简单、推广性能好、优化求解时具有惟一最优解等优点,本文将用SVM的相关理论来解决多观测样本二分类问题,确定多观测样本的类别。根据SVM的原理可知,SVM要解决的数学问题为
 |
(7) |
而从多观测样本二分类问题的描述可知,二分类问题中的所有数据只属于2个类别,数据的标签集为{-1, +1},设多观测样本集X(u)的标签为y,则y=-1或y=+1。因此可以通过假设多观测样本的标签来增加式(7)的约束条件:
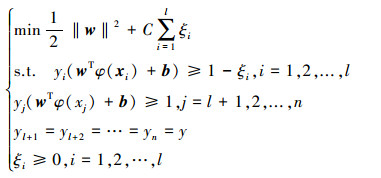 |
(8) |
可以先假设y=-1,求解得到目标函数值g1。再假设y=+1,求解得到目标函数值g2。只有当假设的标签与多观测样本的实际标签相同时,相应得到的目标函数值才是最优解。因此,可以通过比较两次得到的目标函数值来确定待测试的多观测样本的标签。如式(9)所示:
 |
(9) |
为求解式(8)所述的优化问题,引入拉格朗日函数L:
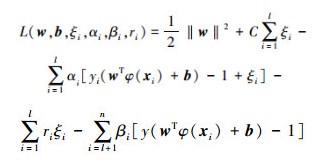 |
(10) |
式中:αi、βi、ri为Lagrange系数,αi≥0,βi≥0,ri≥0,ξi≥0。要使函数L关于w、b、ξi最小化,由极值存在的必要条件可知,函数L的极值满足下列条件:
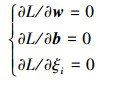 |
(11) |
解方程(11)可得
 |
(12) |
将式(12)代入式(10)得到优化问题式(8)的对偶形式,即关于αi、 βj的最大化函数:
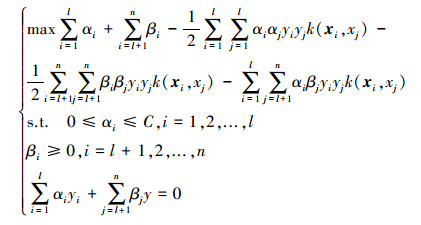 |
(13) |
若设Y=[y1 … yl yl+1 … yn]T,因为yl+1=yl+2= … =yn=y,所以Y=[y1 … yl y … y]T。令O=[1 1… 1],A=[α1 …αlβl+1 … βn]T, 则式(13)变为
 |
(14) |
可以看到,通过求解式(14)可以能得到两次标签假设对应的目标函数值g1和g2,从而根据式(9)确定待测试的多观测样本的标签。
2.3 基于SVM的多观测样本二分类的算法描述基于SVM的多观测样本二分类的算法如下:
输入:
X(l)、 Y(l):已标记样本集和它的标签集;
X(u):多观测样本集;
l:已标记样本的数目;
m:多观测样本数目。
输出:

处理:
1)由X(l)和X(u)得到样本矩阵X, X⊂Rn×d,由Y(l)得到标签矩阵Y;
2)计算样本矩阵X对应的核矩阵K;
3)设y=-1, 求解优化问题:max OA-AT((YYT)·K)A/2,得到g1; 设y=+1, 求解优化问题:max OA-AT((YYT)·K)A/2,得到g2;
4)若g1>g2则

为了验证基于SVM的多观测样本二分类算法的有效性,首先在手写数字数据库上进行实验。同类数字不同形式的手写图像组成多观测样本集,对此类样本集进行分类。实验中,使用2种不同的数据库:Binary手写数字数据库和USPS手写数字数据库。Binary数据库包含0~9共10类数字的手写图像,每类数字有39个样本,每个样本用大小为20×16的二值图像表示。USPS数据库由0~9共10类手写数字组成,每类数字有1 100个样本,每个样本用大小为16×16的灰度图像表示。
模式变换的鲁棒性是多观测样本分类的一种重要特性。可以使用虚拟样本来扩充已标记样本集,从而加强分类算法的抗变换性。虚拟样本一般通过原始样本的变换产生,虚拟样本的类别与原始样本相同,因此是已知标签的已标记样本。通过在数据集中添加虚拟样本,分类算法对测试样本的鲁棒性更强。因此,在本文所提的算法中使用这一方法,在原始数据集中添加大小为nvs的样本集X(vs),数据集变为:X={X(l), X(vs), X(u)}。实验中,核函数选用高斯核函数,即: 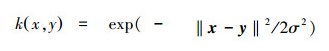
对于每类数字,首先从对应样本中随机抽取2个样本组成训练集,剩下的样本组成测试集。再对训练集中的每个样本做连续的4次旋转变换,得到的样本放在训练集中,其中旋转角θ从[-40°, 40°]的均匀采样序列中得到。这样的区间能避免“6”和“9” 2类数字的混淆。为了建立每类数字的多观测样本数据集X(u),从每类数字的测试集中随机选取一个样本并对这个样本进行旋转变换,旋转角θ∈[-40°, 40°]。每次测试时,选取2类不同的数字进行实验,共有45种组合,即(0, 1), (0, 2), …, (7, 8), (7, 9), (8, 9)。再由这2类数字的训练样本共同组成算法的训练集X(t),而对应的测试集作为算法的测试集,即多观测样本。该实验对不同大小的多观测样本进行了实验,样本数m=[5:5:40]。对于不同大小的数据集X(u),45种组合中的每个组合进行10次随机实验,每个组合要对2个测试集进行测试,所以实验中的每个结果都是900次随机实验的均值,如图 2所示。

|
| 图 2 在2种手写数字数据库上的识别率 Fig. 2 Classification results measured on two different handwritten digit data sets |
从实验结果可以看出本文SVM算法在Binary数据库和USPS数据库上的识别率很高,尤其在USPS数据库上,当样本不少于10时识别率为100%,这就说明基于SVM的多观测样本二分类算法的可行性。分析数据可得:算法的识别率随着多观测样本数目的增大而提高,因为增加多观测样本的数目能提供更多的某特定类别的信息,从而更加准确地判断类别。
3.2 物体图像分类下面在物体图像数据库上验证基于SVM的多观测样本二分类算法的有效性,实验中同一物体的不同观测图像作为此类物体的多观测样本。并将本文算法与经典的多观测样本分类算法进行对比:
1)KLD[2](KL-divergence):该方法是典型的基于密度估计的统计方法,把所有样本集看作是独立同分布的高斯随机变量,然后通过计算样本集间KL散度完成多观测样本的分类。实验中,协方差矩阵特征向量的长度按能量的96%来选取。
2)MSM[6](mutual subspace method):MSM是典型的子空间方法,该方法中的每个图像集用子空间来表示,而子空间通过主成分即协方差矩阵获得,把训练集与测试集之间的主成分角[17]作为相似性度量。实验中,当样本数目小于9时候,协方差矩阵的特征向量长度等于样本数目,否则设为9。
3)KMSM[8](kernel mutual subspace method):KMSM是MSM在非线性空间的扩展,该方法考虑了图像集的非线性。与MSM不同的是,在用线性子空间建模之前,KMSM需要先把图像样本非线性地映射到高维特征空间。也就是说,KMSM用KPCA来取代PCA,从而获得了数据的非线性。KMSM方法中,使用高斯核函数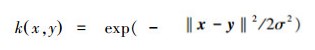
实验选用ETH-80物体识别数据库,ETH-80含有8个种类的图像:苹果、车子、牛、杯子、狗、马、梨和西红柿(如图 3(a)所示)。每个种类又含有10个物体类(例如,狗有10个不同的品种),每个物体类中包含该物体不同角度的41张图像,例如图 3(b)显示了狗这一种类中一个物体类的所有图像。数据库中的所有图像大小为128×128,为了简化计算,对图像重新采样,使其大小为32×32。

|
| 图 3 ETH-80数据库的样本图像 Fig. 3 Sample images from the ETH-80 database |
每个种类的训练样本集由其10个物体类均随机抽取的10张图像组成,即每个种类的训练样本集含有100个样本,而剩余的31张图像组成每个物体类的测试集。实验中,从八大种类中选取2个不同的种类进行分类测试,共有28种组合,即(1, 2), (1, 3), …, (6, 7), (6, 8), (7, 8)。由这2个种类的训练样本共同组成算法的训练集X(l),再分别为这2个种类构建测试集:从每个种类对应的10个物体类中随机选取一个物体类,再从此物体类中选取10个样本组成多观测样本,即为该种类的测试集。对28种组合中的每个组合进行10次随机实验,每个组合要对2个测试集进行测试,所以实验中的每个结果都是560次随机实验的均值, 如表 1所示。
| /% | ||||
| 算法 | KLD | MSM | KMSM | 本文SVM |
| 识别率 | 85.714 | 97.500 | 91.071 | 98.036 |
实验结果表明,本文SVM算法在ETH-80数据库上的识别率很高,并且该算法优于其他3种算法,这就说明了基于SVM的多观测样本二分类算法的有效性。
4 基于视频的人脸识别 4.1 实验数据集为了验证基于SVM的多观测样本二分类算法的有效性,在基于视频序列的人脸识别问题中进行实验,把视频中不同的视频帧作为同一个人的多观测样本。由于视频中人的头部姿势,人脸表情和光照都是变化的,所以本节是在真实的环境中验证所提算法的有效性。把所提算法与4.2节中描述的KLD, MSM和KMSM进行比较。由于实验中所用视频序列的视频帧在时间上是连续的,因此,该算法同样适用于基于图像集的人脸识别问题。
实验中,使用2个数据库:VidTIMIT数据库[18]和Honda/UCSD[19]数据库的第1部分。VidTIMIT数据库包含了43个人在3个时间段的人脸视频序列,其中第1个和第2个时间段间隔7天,第2和第3个时间段间隔6天。每一个视频序列中,被拍摄者头部在不断运动:向左,向右,回到中间,再向下,向上,再回到中间位置。Honda/UCSD数据库包含了20个人的59个视频序列,每个人有2~5个视频序列。与VidTIMIT数据库不同的是,Honda/UCSD数据库的被拍摄者以不同的速度自由移动头部,同时脸部表情也在不断地变化。在两个数据库的预处理中,首先用Viola P的人脸检测方法[20]从视频序列的视频帧中提取人脸区域。为了简化计算,把得到的人脸图像重新采样,使其大小为32×32。
4.2 基于VidTIMIT数据库的人脸识别首先在VidTIMIT数据库上对本文算法进行测试。图 4显示了VidTIMIT数据库中一些样本图像。

|
| 图 4 VidTIMIT数据库中的样本图像 Fig. 4 Sample images in the VidTIMIT database |
由于数据库含有3个时间段的视频序列,因此采用下面的标准度量算法的性能:
 |
式中:e(i, j)表示第i个时间段的数据作为训练集,第j个时间段的数据作为测试集时的分类正确率。也就是说e是以下6次实验的平均正确率,即(1, 2), (1, 3), (2, 1), (2, 3), (3, 1)和(3, 2)。在这6次实验的每次实验中,选取2种不同类别的数据进行实验,共有45种组合,即(1, 2), (1, 3), …, (9, 8), (9, 10)。再由这2类在第i个时间段中的图像集共同组成算法的训练集X(l),而这2类在第j个时间段的图像集作为算法的测试集,即多观测样本。该实验对不同大小的多观测样本进行了实验,样本数目m=[4:4:16]。对于不同数目的多观测样本数据集X(u),45种组合中的每个组合都有2个测试集,因此每个组合要进行2次测试。所以实验中的每个e(i, j)都是90次实验的均值, 每个结果e是540次随机实验的结果,实验结果如表 2所示。
| /% | ||||
| 样本数目m | KLD | MSM | KMSM | 本文SVM |
| 4 | 50.600 | 72.965 | 86.157 | 97.287 |
| 8 | 88.410 | 89.277 | 92.229 | 98.828 |
| 12 | 94.630 | 95.995 | 95.496 | 99.148 |
| 16 | 96.630 | 96.742 | 96.244 | 99.003 |
图 5用柱形图表示了实验结果,本文SVM算法在VidTIMIT数据库上的识别率很高。由图 5可知,对不同数目的观测样本,KLD、MSM和KMSM 3种算法的识别率变化较大,而本文SVM算法的识别率变化不大,这说明基于SVM的多观测样本二分类算法对不同数目的多观测样本具有更好的鲁棒性。

|
| 图 5 在VidTIMIT数据库上的识别率 Fig. 5 Recognition results on the VidTIMIT database |
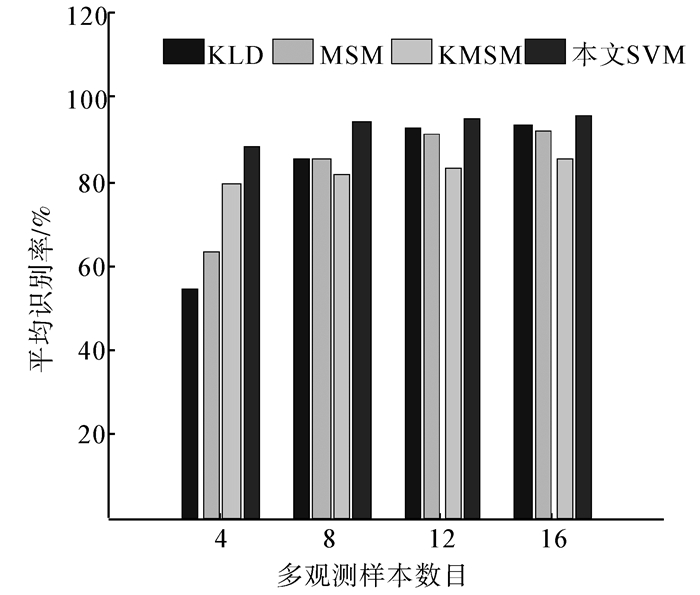
在Honda/UCSD数据库上进一步验证本文SVM算法的有效性。图 6显示了Honda/UCSD数据库中一些样本图像。实验中,选取19个人所对应的视频序列进行实验。实验中,选取2种不同类别的数据进行实验,共有171种组合,即(1, 2), (1,3), …, (17, 18), (17, 19), (18, 19)。由这2类数据的训练样本共同组成算法的训练集X(l),而对应的测试集作为算法的测试集,即多观测样本。该实验对不同大小的多观测样本进行了实验,m=[4:4:16]。对于不同大小的数据集X(u),171种组合中的每个组合都有2个测试集,因此每个组合要进行2次测试。所以实验中的每个结果都是342次实验的均值,如表 3所示,并用柱形图表出来(如图 7)。

|
| 图 6 Honda/UCSD数据库中的样本图像 Fig. 6 Sample images in the Honda/UCSD database |
| /% | ||||
| 样本数目m | KLD | MSM | KMSM | 本文SVM |
| 4 | 54.678 | 63.158 | 79.825 | 88.596 |
| 8 | 85.371 | 85.088 | 82.164 | 94.444 |
| 12 | 92.690 | 90.936 | 83.333 | 95.322 |
| 16 | 93.860 | 92.105 | 85.673 | 95.906 |
|
| 图 7 在Honda/UCSD数据库上的识别率 Fig. 7 Recognition results on the Honda/UCSD database |
实验结果表明,相比于以往的KLD、MSM和KMSM算法,本文SVM算法获得最高的识别率。这进一步说明了基于SVM的多观测样本二分类算法的有效性。
5 结束语本文提出基于SVM的多观测样本分类算法,该算法首先进行类别假设,然后求解优化问题得到相应的目标函数值,把目标函数值作为分类依据来实现多观测样本的二分类。实验结果表明本文算法在手写数字识别、物体识别和人脸识别中都能取得较好的分类效果,为模式识别问题提供了一种新的方法。但是本文针对的是二分类问题,如何在该算法的基础上实现多分类仍是需要进一步的研究。
| [1] | KIM T K, KITTLER J, CIPOLLA R. On-line learning of mutually orthogonal subspaces for face recognition by image sets[J]. IEEE Transactions on Signal Processing , 2010, 19 (4) : 1067-1074 |
| [2] | SHAKHNAROVICH G, FISHER J W, DARREL T. Face recognition from long-term observations[C]//European Conference on Computer Vision(ECCV). San Diego, USA, 2002, 3: 851-868. |
| [3] | ARANDJELOVIC O, SHAKHNAROVICH G, FISHER J, et al. Face recognition with image sets using manifold density divergence[C]//IEEE International Conference on Computer Vision and Pattern Recognition(CVPR). San Diego, USA, 2005, 1: 581-588. |
| [4] | CARDINAUX F, SANDERSON C, BENGIO S. User authentication via adapted statistical models of face images[J]. IEEE Transactions on Signal Processing , 2006, 54 (1) : 361-373 DOI:10.1109/TSP.2005.861075 |
| [5] | ARANDJELOVIC O, CIPOLLA R. Face recognition from face motion manifolds using robust kernel resistor-average distance[C]//IEEE Workshop on Face Processing in Video. Washington D C, USA, 2004, 5: 88-93. |
| [6] | YAMAGUCHI O, FUKUI K, MAEDA K, et al. Face recognition using temporal image sequence[C]//IEEE International Conference on Automatic Face and Gesture Recognition. Nara, Japan, 1998: 318-323. |
| [7] | FUKUI K, YAMAGUCHI O. Face recognition using multi-viewpoint patterns for robot vision[C]//International Symposium on Robotics Research. Siena, Italy, 2005, 15: 192-201. |
| [8] | SAKANO H, MUKAWA N. Kernel mutual subspace method for robust facial image recognition[C]//Fourth International Conference on Knowledge-based Intelligent Engineering Systems and Allied Technologies. [S.l.], 2000, 1: 245-248. |
| [9] | WOLF L, SHASHUA A. Learning over sets using kernel principal angles[J]. Machine Learning Research , 2003, 4 (10) : 913-931 |
| [10] | KIM T K, KITTLER J, CIPOLLA R. Discriminative learning and recognition of image set classes using canonical correlations[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence , 2007, 29 (6) : 1005-1018 DOI:10.1109/TPAMI.2007.1037 |
| [11] | KIM T K, ARANDJELOVIC O, CIPOLLA R. Boosted manifold principal angles for image set-based recognition[J]. Pattern Recognition , 2007, 40 (9) : 2475-2484 DOI:10.1016/j.patcog.2006.12.030 |
| [12] | LI X, FUKUI K, ZHENG N N. Image-set based face recognition using boosted global and local principal angles[C]//9th Asian Conference on Computer Vision(ACCV).Xi'an, 2010: 323-332. |
| [13] | WANG R P, SHAN S G, CHEN X L, et al. Manifold-manifold distance with application to face recognition based on image Set[C]//IEEE International Conference on Computer Vision and Pattern Recognition(CVPR). Anchorage, Alaska, USA, 2008: 1-8. |
| [14] | CHU W S, CHEN J C, LIEN J. Kernel discriminant transformation for image set-based face recognition[J]. Pattern Recognition , 2011, 44 (8) : 1567-1580 DOI:10.1016/j.patcog.2011.02.011 |
| [15] | KOKIOPOULOU E, PIRILLOS S, BROSSARD P. Graph-based classification of multiple observation sets[J]. Pattern Recognition , 2010, 43 (12) : 3988-3997 DOI:10.1016/j.patcog.2010.07.016 |
| [16] | VAPNIK V. The nature of statistical learning theory[M]. New York: Springer-Verlag, 1995 : 21 -32. |
| [17] | GOLUB G H, LOAN C V. Matrix computations[M]. 3rd ed Baltimore: The John Hopkins University Press, 1996 : 15 -16. |
| [18] | SANDERSON C. Biometric person recognition: face, speech and fusion, VDM-Verlag, 2008. |
| [19] | LEE K C, HO J, YANG M H, et al. Video-based face recognition using probabilistic appearance manifolds[C]//IEEE International Conference on Computer Vision and Pattern Recognition (CVPR). Madison, USA, 2003: 313-320. |
| [20] | VIOLA P, JONES M. Robust real-time face detection[J]. International Journal of Computer Vision , 2004, 57 (2) : 137-154 DOI:10.1023/B:VISI.0000013087.49260.fb |



