在生产实践领域和科学计算研究中,存在大量涉及函数积分的求解问题,比如PID调节器设计、桥梁设计、计算机图形学、金融数学等,因此研究数值积分问题对科学研究和工程实践具有重要参考价值。目前,求解函数的数值积分的方法有许多,常用的传统数值积分方法有Simpson法、Newton法、梯形法、矩形法、Remberg法、Gauss法等[1-3],但这些传统的方法在工程技术和科学研究中都存在一定程度的不足,比如积分精度不高、计算量较大、系数和节点的计算比较困难、收敛性得不到保证、求解被积函数的原函数非常困难等问题。近年来,随着智能算法的发展,有学者利用智能算法求解函数的数值积分问题,从而克服了传统的数值积分方法的缺陷。如2008年,周永权等人提出了基于进化策略求解任意函数数值积分[4],该算法能快速有效地求出任意函数的数值积分值;2009年,韦杏琼等[5]提出了一种基于粒子群算法的不等距节点数值积分方法,该算法能求解任意函数的数值积分值,对被积函数要求低,计算精度较高;同年,聂黎明等[6]提出一种基于人工鱼群算法求解任意函数的数值积分方法,该算法对参数选取不敏感且对初始值无要求,计算积分精度较高;2013年陈欢[7]提出了一种基于杂草算法求解任意函数的数值积分方法,该算法对积分精度有所提高。上述智能算法都在一定程度上解决了传统数值积分方法的不足,取得了较大的成功,但在积分精度、鲁棒性、收敛性等方面仍存在不足。同时,目前国内外对蝙蝠算法在函数数值积分方面的研究较少。
1 蝙蝠优化算法 1.1 基本蝙蝠优化算法蝙蝠算法(bat algorithm, BA)[8]是YANG X S 2010年提出的一种新的群智能优化算法。是模拟蝙蝠采用一种声呐来探测猎物、避免障碍物的生物学特性发展而来的一种新颖的群智能优化算法,具有并行性、收敛速度快、分布式等特征。目前,BA算法作为一种新的群智能优化算法,已广泛应用于自然科学、工程科学与生产实践中,如PFSP调度问题[9]、k_均值聚类优化[10]、工程优化[11]、多目标优化[12]等问题中。但该算法存在着缺乏变异机制[13]、易陷入局部极小、后期收敛速度慢与收敛精度低等缺点,使其在很多领域的应用被严重地制约了,因此在具体的实际应用中需要经常对它进行改进。
1.2 具有差分进化策略的蝙蝠算法 1.2.1 差分进化算法差分进化算法(differential evolution,DE)[14]是一种基于群体差异的启发式全局智能优化算法,它是K Price和R Storn在1997年为求解切比雪夫多项式而提出的。其设计思想是:应用当前种群个体的差异来重组得到中间种群,然后再利用后代个体与父代个体之间的相互竞争来产生下一代新的种群。其优点主要有收敛速度快、需待定的参数较少、不易陷入局部最优、易与其他智能算法融合,并构造出具有性能更优的群智能优化算法。
1.2.2 DEBA算法的设计思想本文基于基本的BA算法,引入差分进化策略,融合其各自的优点,提出了基于差分进化策略的改进BA算法(differential evolution bat algorithm,DEBA)。考虑到随机初始种群个体会影响算法的计算量,另外,R L Haupt等[15]指出,在基于种群迭代搜索的全局优化算法中,在迭代初期,多样性较好的种群对提高算法的全局寻优能力很有帮助。因此,本文提出的DEBA算法在算法的迭代初期就把变异等算子融入进来,从而保证了迭代初期种群的多样性。
对基本的蝙蝠算法的深入剖析得知,由于算法缺乏相应的变异机制,使得基本的蝙蝠算法具有收敛精度低、易陷入局部极小等缺陷。为了克服这些不足,把差分进化策略融入到基本的蝙蝠算法中来,从而形成了本文算法,它跟基本的蝙蝠算法最显著的区别在于使原来没有变异操作的基本蝙蝠算法具有变异机制。
DEBA算法的设计思想:在基本的蝙蝠算法基础上,经过演化后的蝙蝠位置xit不是直接进入下一次(t+1)迭代,而是继续对其进行差分进化,通过变异机制来获得种群中优秀个体与当前个体之间的差异,从而引导个体的演化方向,使其向种群中的优秀个体靠近,在得到新的蝙蝠位置后,再进入下一次迭代,继续利用基本的蝙蝠算法进行搜索和位置更新。这样就增加了种群的多样性,使其避免陷入局部最优而获得全局最优解,同时也提高了收敛速度和收敛精度。
1.2.3 DEBA算法实现步骤DEBA算法的具体实施步骤如下:
1)初始化DEBA算法的各个参数。
2)根据目标函数计算种群个体的适应度函数值,确定当前的最优值及最优解。
3)利用式(1)~(3)对蝙蝠的搜索脉冲频率、速度和位置进行更新:
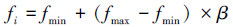 |
(1) |
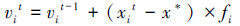 |
(2) |
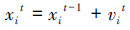 |
(3) |
式中:β∈[0, 1]是均匀分布的随机数;fi是蝙蝠i的搜索脉冲频率,fi∈[fmin,fmax];vit、vit-1分别表示蝙蝠i在t和t-1时刻的速度;xit、xit-1分别表示蝙蝠i在t和t-1时刻的位置;x*表示当前所有蝙蝠的最优解。
4)对当前最优解进行随机扰动,产生一个新的解,并对新的解进行越界处理。
5)生成均匀分布随机数rand,如果rand < Ai且f(xi) < f(x*),则接受4)产生的这个新解,然后按式(4)~(5)对ri和Ai进行更新:
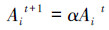 |
(4) |
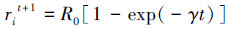 |
(5) |
6)利用差分进化算法以每一个蝙蝠位置为初始点进行变异、交叉、选择操作,得到新的蝙蝠位置。
7)根据种群蝙蝠个体的适应度值优劣,来更新种群的最优值和种群的最优解。
8)在算法完成一次迭代后,进入下一次迭代之前,判断算法是否满足终止条件,如满足条件,则退出程序并输出种群的最优解及种群的最优值,否则,转3)。
2 DEBA算法性能实验仿真与分析为了验证本文算法的寻优精度、收敛速度、鲁棒性等性能优于基本的蝙蝠优化算法,本文利用4个不同维数的经典测试函数进行性能比较测试。测试函数[16-17]及其参数如下:
1) Sphere函数:D=10, -100≤xi≤100,函数的理论最优值为0。
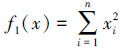 |
2) Rastrigrin函数:D=10, -5.12≤xi≤5.12,函数的理论最优值为0。
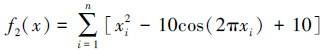 |
3) Rosenbrock函数:D=10, -30≤xi≤30,函数的理论最优值为0。
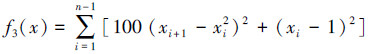 |
4) Schaffer F6函数:D=2, -100≤xi≤100,函数的理论最优值为-1。
 |
在本文算法中参数设置如下:最大脉冲率R0=0.5,最大脉冲音量A0=0.25,脉冲频率增强系数gama=0.05,脉冲频率范围[0, 2],尺度因子F=0.5,脉冲音量衰减系数alf=0.95,交叉概率CR=0.1,种群数最大为200,最大迭代次数为1 000。
2.1 固定演化迭代次数的性能比较为了防止算法的偶然性带来的误差,分别对每个函数独自执行20次,取其最优值、平均值、最差值和标准差,并与基本的蝙蝠算法进行比较,测试结果如表 1所示。
| 函数 | 算法 | 最优值 | 平均值 | 最差值 | 标准差 |
| f1(x) | DEBA | 9.69563834601188E-19 | 5.84379322609028E-18 | 1.62619389692447E-17 | 4.83833694643861E-18 |
| BA | 2.16605159265E+03 | 1.24378646804E+04 | 3.68689654162E+04 | 7.91305595959E+03 | |
| f2(x) | DEBA | 0 | 0 | 0 | 0 |
| BA | 4.87664433735E+01 | 9.77629405876E+01 | 1.78104931825E+02 | 3.24392513245E+01 | |
| f3(x) | DEBA | 22.86069418838456 | 55.24989150912832 | 88.59947945489543 | 17.80577852011065 |
| BA | 4.13821313748E+03 | 1.01326679645E+07 | 5.38275134994E+07 | 1.37257696079E+07 | |
| f4(x) | DEBA | -1 | -0.99992590333598 | -0.99943890712016 | 1.32120767991106e-04 |
| BA | -0.92181081785627 | -0.64017500307743 | -0.51119158750609 | 1.2404397445565 e-01 |
由表 1可以获得,对f1单峰函数,DEBA比BA的最优值提高了22个数量级,平均值提高了22个数量级,标准差提高了21个数量级;对高维、复杂的多峰函数f2,DEBA的最优值达到了理论最优值,平均适应值提高了1个数量级,标准差提高了1个数量级;对单峰病态函数f3,DEBA比BA的最优值提高了2个数量级,平均适应值提高了6个数量级,标准差提高了6个数量级;对强烈振荡的多峰函数f4,DEBA的最小适应值达到了理论最优值,平均适应值提高了0.35,标准差提高了3个数量级。由仿真实验结果表明,本文算法(DEBA)效果较好,并对高维多峰函数也是可行有效的。
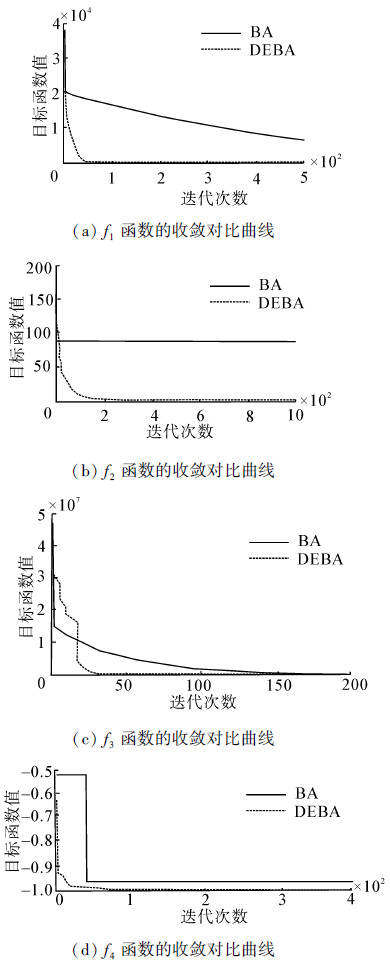
图 1是本文算法与基本的蝙蝠算法的收敛曲线对比图。可以看出本文算法在收敛速度、迭代次数、收敛精度等性能上显著优于基本的蝙蝠算法,而且对于复杂多极值点函数,本文算法能收敛到函数的理论全局最优解。
|
| 图 1 DEBA与BA的收敛曲线对比 Fig. 1 Comparison of convergence curves of DEBA and BA |
一个好的智能优化算法,时间复杂度应该比较低。由于篇幅限制,这里只选用了测试函数f3对本文算法的时间复杂度进行测试分析,取相同的种群数(40)、独立运行次数(20次),计算所需要的平均运行时间,仿真结果如表 2所示。从表 2的平均运行时间来看,虽然DEBA算法多了利用差分进化策略进行变异操作,但在不同维数情况下DEBA算法的平均运行时间比BA算法的平均运行时间略长一些,说明本文算法是可行和有效的。
| 维数 | DEBA | BA |
| 10 | 0.9555 | 0.3276 |
| 30 | 1.0109 | 0.3526 |
| 50 | 1.1069 | 0.3853 |
3 DEBA算法求解数值积分算法
通过上述实验仿真表明,改进的蝙蝠算法DEBA具有收敛精度高、收敛速度快等特性。针对目前数值积分方法存在的缺陷,利用DEBA算法求数值积分,其基本思想是:在积分区间[a,b]随机生成NP个节点位置,然后通过本文算法优化这些点的位置,最终获得精度较高的积分值,实现步骤为
1)在积分区间随机生成NP个D维个体的种群,并确定种群中的每个个体的表达式,个体的表示形式为(X, V)=((x1,x2,…,xD),(v1,v2,…,vD))。
2)计算适应度。对积分区间内的每个个体的D维分量进行升序排列,接着分别计算D+2个节点相邻之间的距离dj,j=1,2, …,D+1,然后计算D+1个小段中间节点和D+2个节点的函数值,并比较每小段中间节点、左端点和右端点的函数值,记下最大的函数值为Maxj,最小的函数值为Minj, j=1, 2, …, D+1,每个个体的适应度定义为:f(i)=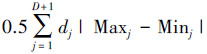
3)对算法的终止条件进行判断,假如终止条件不成立,则算法往下继续执行,如终止条件满足,算法停止运行,并输出种群的最优个体,同时求出函数的积分值。
4)更新蝙蝠种群。
5)重复运行4),直到终止条件满足为止,输出种群的最优个体,并把它作为结果。
6)算法停止执行时,算法最终所求出的函数积分值近似于
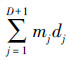 |
(6) |
式中,(d1,d2,…,dD+1)是积分区间的D+1个小段对应的距离,(m1,m2,…,mD+1)为积分区间的D+1个小段对应的中间点所对应的函数值。
4 数值积分仿真实验与分析为验证DEBA算法求解数值积分问题的有效性和正确性, 选取了文献[1-7]中给出的一些算例, 并与传统的梯形法、Simpson方法、Composite Simpson方法、Romberg方法及一些智能算法(粒子群算法, 杂草算法、人工鱼群算法)数值积分方法进行比较。
例1 取N=15, D=60,分别计算6个函数:x2、x4、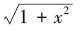
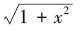
| 函数 | x2 | x4 | 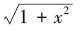 | 1/1+x | sin(x) | ex |
| 精确值 | 2.667 | 6.400 | 2.958 | 1.099 | 1.416 | 6.389 |
| 本文算法 | 2.666 985 73 | 6.401 201 | 2.958 169 0 | 1.098 754 | 1.416 082 | 6.388 921 |
| IWO | 2.666 33 | 6.398 65 | 2.957 81 | 1.098 59 | 1.416 32 | 6.388 73 |
| PSO | 2.666 | 6.398 | 2.958 7 | 1.098 5 | 1.416 | 6.388 7 |
| AFS | 2.666 593 | 6.399 501 | 2.957 868 | 1.098 598 | 1.416 173 | 6.388 949 |
| FN | 2.667 | 6.399 5 | 2.957 89 | 1.098 6 | 1.416 | 6.389 |
| ES | 2.666 | 6.398 | 2.957 7 | 1.098 | 1.416 | 6.388 |
| NN | 2.665 | 6.393 | 2.959 | 1.101 | 1.415 | 6.388 |
| Simpson | 2.667 | 6.667 | 2.964 | 1.111 | 1.425 | 6.421 |
| 梯形法 | 4.000 | 16.000 | 3.326 | 1.333 | 0.909 | 8.389 |
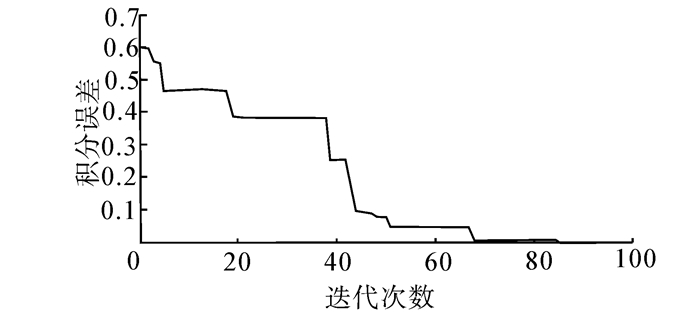
|
| 图 2 函数x4的积分误差变化曲线 Fig. 2 The integral error change curve of function x4 |
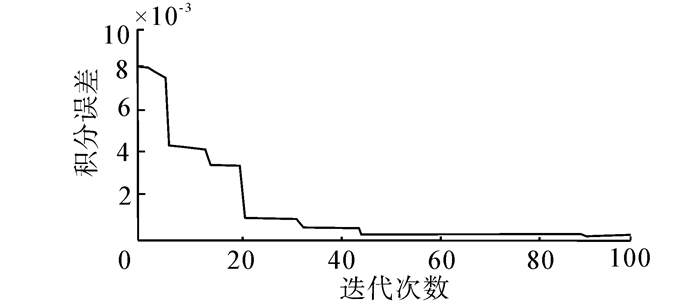
|
图 3
函数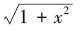 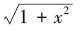 |
例2 计算奇异函数积分:
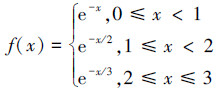 |
该奇异函数的精确积分值是1.546 036。本文取N=15, D=60,获得该函数的积分值与文献[4-7]、文献[19]、文献[20]的计算结果对比如表 4所示。DEBA算法求解该函数的积分误差变化曲线如图 4。
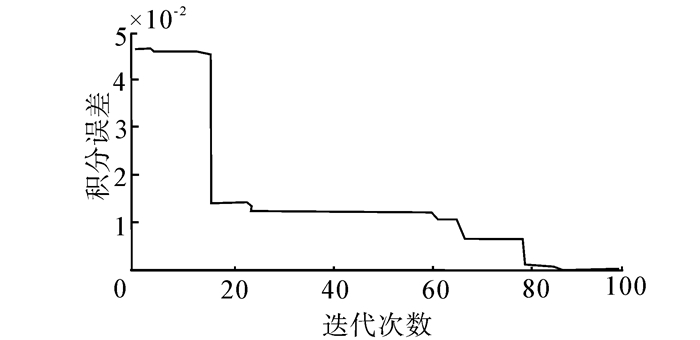
|
| 图 4 例2的积分误差变化曲线 Fig. 4 The integral error change curve of example 2 |
例3 求解函数积分∫01e-x2dx
由于被积函数的原函数不是初等函数,因此不能用牛顿—莱布尼茨公式进行计算[5]。例3的函数的精确积分值是0.746 824。本文取N=15, D=200,获得该函数的积分值与文献[4-7]、文献[19]、文献[20]的计算结果对比如表 5所示。DEBA算法求解该函数的积分误差变化曲线如图 5所示。
| 算法 | 函数积分值 |
| 本文算法 | 0.746 826 954 460 4 |
| PSO | 0.746 866 |
| IWO | 0.746 834 |
| AFS | 0.7468 273 04 |
| ES | 0.746 83 |
| 矩形法 | 0.777 82 |
| 梯形法 | 0.746 21 |
| Simpson | 0.746 83 |
|
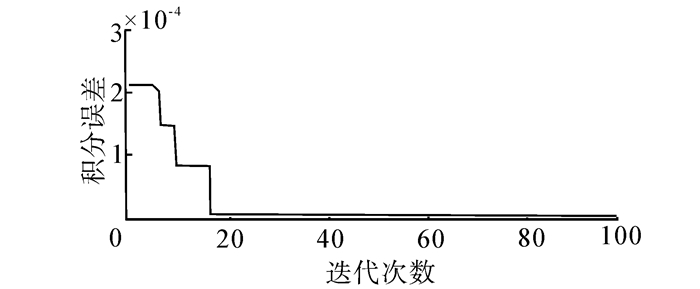
| 图 5 例3的积分误差变化曲线 Fig. 5 The integral error change curve of example 3 |
例4 计算积分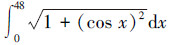
该积分函数在利用Romberg方法进行计算时遇到了困难[18]。用Composite Simpson rule法计算时,把积分区间划分为100个等距子区间,计算结果为58.470 821 5[18]。例4的函数的精确积分值是58.470 469 1。运用DEBA算法,取N=15, D=100,得该函数积分值与文献[4-7]、[19]、[20]的结果对比如表 6。DEBA法求解该函数积分误差变化曲线如图 6。
| 算法 | 函数积分值 |
| 本文算法 | 58.470 505 372 351 |
| PSO | 58.470 24 |
| IWO | 58.470 492 |
| AFS | 58.470 444 83 |
| ES | 58.470 65 |
| FN | 58.470 5 |
| 梯形法 | 58.520 9 |
| Simpson | 58.470 821 5 |
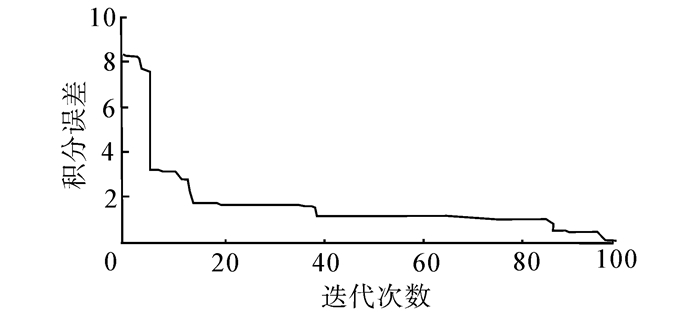
|
| 图 6 例4的积分误差变化曲线 Fig. 6 The integral error change curve of example 4 |
例5 计算振荡函数积分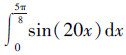
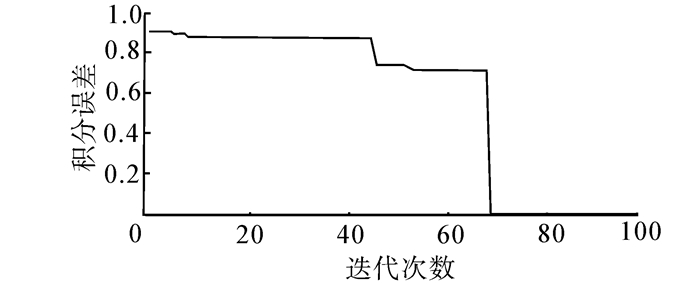
该函数的精确积分值为0.05,本文取N=15, D=120,计算的结果为0.049 992 860 744 717 2。在用复化梯形公式计算此积分[21]时,为了使此函数的积分误差不超过10-3,则至少应该取503个点,求解中的计算工作量非常大,运用神经网络计算的结果为0.049 92[22],利用粒子群计算的结果为0.050 038[5],采用杂草算法获得的结果为0.050 025 239 093 085[7]。DEBA算法求解该函数的积分误差变化曲线如图 7所示。
|
| 图 7 例5的积分误差变化曲线 Fig. 7 The integral error change curve of example 5 |
例6 计算振荡函数积分∫01xsinxsin(100x)dx
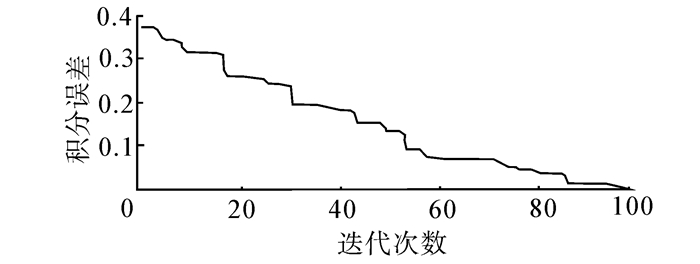
该振荡函数积分的精确值为-0.007 327 9,利用粒子群进行计算得到的结果为-0.007 340 9[5],采用人工鱼群算法计算得到的结果为-0.007 332 084 927 92[6],运用杂草算法计算得到的结果为-0.007 362 73[7],本文取N=15, D=360,计算得到的结果为-0.007 335 411 855 213 67。DEBA算法求解该函数的积分误差变化曲线图如图 8。
|
| 图 8 例6的积分误差变化曲线 Fig. 8 The integral error change curve of example 6 |
通过上述6个不同数值积分算例对本文DEBA算法的正确性和有效性进行的测试结果分析得到:从表 3可以得知,对算例1中的6个普通函数进行数值积分,DEBA算法相比目前的数值积分方法所求的积分值精度都要高,且优势明显;从表 4可以得知,对算例2的奇异函数积分,DEBA算法相比神经网络算法(NN)精度高2个数量级,比杂草算法(IWO)和进化策略(ES)精度高1个数量级,比粒子群算法(PSO)、人工鱼群算法(AFS)、三角函数作为泛函神经元(FN)3种方法的精度都要略高一些;从表 5可以得知,对算例3的积分,DEBA算法分别比矩形法、梯形法精度高4个数量级和2个数量级,比粒子群算法和杂草算法精度高1个数量级,比进化策略、人工鱼群算法和Simpson法的精度都要略高一些;从表 6可以得知,对算例4的积分,DEBA算法相比梯形法精度高3个数量级,比进化策略、粒子群算法和Simpson法精度高1个数量级,跟杂草算法、人工鱼群算法、FN法3种方法相比,积分精度相当,积分误差的数量级都是10-5;对于算例5的振荡函数积分,DEBA算法相比神经网络算法、粒子群算法和杂草算法精度都要高1个数量级;对于算例6的振荡函数积分,DEBA算法比粒子群算法、杂草算法的精度都要高1个数量级,跟人工鱼群算法相比,积分精度相当,积分误差的数量级都是10-5。从图 2~8可以看出,DEBA算法收敛性较好,经过较少的迭代次数就能获得精度较高的积分值。从以上数值积分实验仿真结果表明,DEBA算法是非常有效的。
5 结束语本文提出了基于改进的蝙蝠算法求函数数值积分的新方法DEBA算法,对6个不同数值积分算例进行测试,仿真结果表明,该算法收敛性、计算精度相比目前的数值积分方法优势比较明显,验证了DEBA算法的有效性和可行性,不仅可以对普通函数进行积分,还可以计算振荡积分、奇异积分和被积函数的原函数不是初等函数积分,此方法可看作对目前数值积分方法的一种深入扩展。同时,也可以看作蝙蝠算法应用领域的一种补充。如何利用其他智能算法的优点来改进基本的BA算法,如与花朵授粉算法进行融合;如何扩展BA算法的应用领域,利用BA算法解决离散性问题;对蝙蝠算法的理论研究(如利用Markov链证明蝙蝠算法的收敛性)等问题是今后进一步研究的内容和方向。
| [1] | 薛密. 数值数学和计算[M]. 上海: 复旦大学出版社, 1991 : 191 -195. |
| [2] | 刘玉琏, 傅沛仁. 数学分析讲义[M]. 北京: 高等教育出版社, 1992 : 309 -342. |
| [3] | 华东师范大学数学系. 数学分析[M]. 北京: 高等教育出版社, 2001 : 106 -109. |
| [4] | 周永权, 张明, 赵斌. 基于进化策略方法求任意函数的数值积分[J]. 计算机学报 , 2008, 31 (2) : 196-205 ZHOU Yongquan, ZHANG Ming, ZHAO Bin. Solving numerical integration based on evolution strategy method[J]. Chinese Journal of Computers , 2008, 31 (2) : 196-205 |
| [5] | 韦杏琼.基于粒子群算法的数值方法研究[D].南宁:广西民族大学, 2009: 11-15. WEI Xingqiong. Research on numerical methods based on PSO[D]. Nanning: Guangxi Uiversity for Nationalities, 2009: 11-15. http://cdmd.cnki.com.cn/article/cdmd-10608-2009255027.htm |
| [6] | 聂黎明, 周永权. 基于人工鱼群算法求任意函数的数值积分[J]. 数学的实践与认识 , 2009, 39 (19) : 127-134 NIE Liming, ZHOU Yongquan. Solving numerical integration based on artificial fish-swarm algorithm[J]. Mathematics in Practice and Theory , 2009, 39 (19) : 127-134 |
| [7] | 陈欢.杂草优化算法的改进分析及应用研究[D].南宁:广西民族大学, 2013:34-39. CHEN Huan. Improvements and applications of invasive weed optimization algorithm[D]. Nanning: Guangxi University for Nationalities, 2013: 34-39. http://cdmd.cnki.com.cn/Article/CDMD-10608-1013247163.htm |
| [8] | YANG Xinshe. A new metaheuristic bat-inspired algorithm[C]//Nature Inspired Cooperative Strategies for Optimization. Berlin: Springer-Verlag, 2010: 65-74. |
| [9] | 盛晓华, 叶春明. 蝙蝠算法在PFSP调度问题中的应用研究[J]. 工业工程 , 2013, 16 (1) : 119-124 SHENG Xiaohua, YE Chunming. Application of bat algorithm to permutation flow-shop scheduling problem[J]. Industrial Engineering Journal , 2013, 16 (1) : 119-124 |
| [10] | KOMARASAMY G, WAHI A. An optimized k-means clustering technique using bat algorithm[J]. European Journal of Scientific Research , 2012, 84 (2) : 263-273 |
| [11] | YANG X S, GANDOMI A H. Bat algorithm: a novel approach for global engineering optimization[J]. Engineering Omputation , 2012, 29 (5) : 464-483 DOI:10.1108/02644401211235834 |
| [12] | YANG X S. Bat algorithm for multi-objective optimization[J]. International Journal of Bio-Inspired Computation , 2011, 3 (5) : 267-274 DOI:10.1504/IJBIC.2011.042259 |
| [13] | 刘长平, 叶春明. 具有Levy飞行特征的蝙蝠算法[J]. 智能系统学报 , 2013, 8 (3) : 240-246 LIU Changping, YE Chunming. Bat algorithm with the characteristics of Levy flights[J]. CAAI Transaction on Intelligent System , 2013, 8 (3) : 240-246 |
| [14] | STORM R, PRICE K. Differential evolution dash a simple and efficient heuristic for global optimization over continuous spaces[J]. Journal of Global Optimization , 1997 (11) : 341-359 |
| [15] | HAUPT R L, HAUPT S E. Practical genetic algorithm[M]. New Jersey: John Wiley & Sons, 2004 : 1 -25. |
| [16] | 李明, 曹德欣. 混合CS算法的DE算法[J]. 计算机工程与应用 , 2013, 49 (9) : 57-60 |
| [17] | 刘佳昆, 周永权. 一种最大最小萤光素值人工萤火虫算法[J]. 计算机应用研究 , 2011, 28 (10) : 3662-3664 LIU Jiakun, ZHOU Yongquan. Glowworm swarm optimization algorithm based on max-min luciferin[J]. Application Research of Computers , 2011, 28 (10) : 3662-3664 |
| [18] | BURDEN R L, FSIRES J D. Numerical Analysis[M]. Toronto: Thomson Brooks/Cole, 2001 : 206 -212. |
| [19] | WANG X H, HE Y G, ZENG Z Z. Numerical integration study based on triangle basis neural network algorithm[J]. Journal of Electronics & Information Technology , 2004, 26 (3) : 394-299 |
| [20] | 韦修喜, 周永权, 蓝晓玲. 一种基于泛函网络求数值积分方法研究[J]. 计算机科学 , 2009, 36 (4) : 224-226, 238 WEI Xiuxi, ZHOU Yongquan, LAN Xiaoling. Numerical integration method study based on function network[J]. Computer Science , 2009, 36 (4) : 224-226, 238 |
| [21] | 丁丽娟, 程杞元. 数值计算方法[M]. 北京: 北京理工大学出版社, 2005 : 165 -204. |
| [22] | 徐理英, 李立军. 数值积分的神经网络算法研究[J]. 系统仿真学报 , 2008, 20 (7) : 1922-1924 XU Liying, LI Lijun. Neural network algorithm for solving numerical integration[J]. Journal of System Simulation , 2008, 20 (7) : 1922-1924 |



