随着信息技术的快速发展和大规模应用,数据的生成速度及存储规模也在快速增长,特别是Web页面、社交网络及物联网的普及和应用,使人们所要存储、处理和分析的数据规模以指数方式递增。如谷歌搜索引擎在2008年索引的网页个数突破1万亿个,沃尔玛最近构建的一个数据仓库的数据规模达到4 PB。在此背景下对大数据的分析和挖掘成为当前的热点研究主题[1]。从算法的层面来看,大数据的机器学习和分析挖掘问题,主要存在以下的问题:
1)数据规模巨大,体现在数据记录个数及维度上,对于很多大数据分析问题,即使是多项式时间复杂度的机器学习算法也不能在人们可接受的时间内得到结果。
2)由于数据集比计算机内存大,导致无法在训练学习器时加载整个训练集,或是出于应用环境的限制,在训练学习器时不能获取整个数据集,数据记录可能按某种速率到来,而且数据产生的规律性会随着时间变化而有所改变。
要解决问题1),主要从2个途径去考虑,其一是降低现有分析算法的时间复杂度,采取一些近似算法,在复杂度和精度方面取得折衷,如Yang等[2]提出了一种决策树快速增量学习方法,通过对决策树的属性选择指标进行近似,使算法能适用于数据流和超大型数据集,其性能和普通版本的决策树相比并没有明显的下降;Jordan[3]对大数据统计推断进行了回顾,并针对大数据分而治之的算法提出了2种设计方法,其中重采样策略是对完整训练集的近似,而分治策略把大数据集数据间的相互关系限制在较小的范围内,最终目的是降低算法的复杂度;其二是对现有算法进行修改,转化为可以并发/并行计算的版本,并利用云计算开发工具,如MapReduce编写可以在云计算平台上运行的程序,通过计算云的强大运算能力,使算法能在可接受的时间内解决大数据分析问题,如Acar等[4]在MapReduce框架中实现了自适应计算的数据流分析算法,通过维护一个数据表跟踪数据集不同部分计算之间的依赖关系,当需要更新时仅需考虑有关联的部分数据,算法有相对较佳的运行效率;Ari等[5]设计了面向数据流的相关分析和关联规则挖掘的云计算算法,能够以批处理和在线的方式把相关分析和关联规则挖掘的任务透明分配到计算云的不同部分,同时计算然后再进行整合。
对于问题2),目前主要解决思路是设计出以往机器学习和挖掘算法的在线学习版本。在线学习原是机器学习的一个研究分支,其目标数据样本以顺序的方式输入学习器,且不对历史数据样本进行保存,算法通过对当前输入的样本进行分析,同步更新学习器,其中神经网络中的感知器模型就是在线学习的经典例子[6]。由于在线学习不用保存以往的数据样本,或仅需保存以往数据样本的某种充分统计量,十分适合大数据分析的应用场景。对于超大型数据集,以顺序方式输入模型,并同步更新学习器;对高速数据流,在线学习可以实现数据的边输入边学习,使学习器模型能够反映出最近一段时间的输入数据规律并进行有效预测。
本文研究大数据环境下的在线核学习(online kernel learning)算法。与传统在线学习不同,本文的工作主要针对大数据流中的核函数学习问题,算法并不直接通过数据样本的分析对学习器进行更新,而是通过在线学习以迭代的方式确定一个最适用于当前数据产生规律的核函数。本文认为,核函数的学习比直接训练学习器有更广泛的适用性,一个合适的核函数可以被嵌入到各种不同核学习器的训练过程,也可以直接用于核主成份分析(kernel PCA)、相关性分析(kernel CCA)或聚类分析等领域。因此,一个有效适用于大数据环境下的核学习算法有重要应用价值。
目前被公开报道的在线核学习研究工作并不多,虽然核学习被广泛用于机器学习的不同应用领域,但核函数的学习问题由于其对分析目标的间接性影响,在大数据分析和挖掘领域中并没有被充分研究,因此研究大数据环境下的核函数学习问题对其他大数据机器学习任务有重要的基础性意义。
本文提出一种适用于大数据流的在线核学习算法,在现有多核学习框架中结合数据依赖核的构建方法,同时进行有监督学习和无监督学习,对于高速数据流中的有标记数据使用一种类似感知器训练的学习策略进行有监督核函数学习,对于所有数据(包括有标记和无标记数据)进行基于数据依赖核的核函数更新策略,实质上进行一种无监督学习,不需要存储和重新扫描历史数据,仅需通过选择的方式维持一个样本工作集,在读取新的数据样本时能以较低的时间复杂度直接更新当前的核函数,适用于大数据环境下的核学习问题,特别是高速大数据流中标记缺失的情形。
1 在线核学习的相关工作核函数学习问题是机器学习研究中的一个分支方向,通过机器学习的方法学习一个针对特定应用背景的核函数,能够大幅提高训练学习器的效果。Gönen等[7]回顾了目前的主要多核学习算法,指出大多数算法所得到核函数组合对学习器的影响差别不大,但是在学习算法的时间复杂度及核函数组合的稀疏性方面却有很大差异,这种差异性在处理大数据的多核学习问题时必须考虑。他们的工作表明通过非线性和数据依赖的方式进行核函数的组合具有更好的性能,数据依赖的核函数修正方式适合于高速无标记的数据流,这是本文在线核学习方法的一个出发点。Orabona等[8]提出了一种多核学习的快速算法,能够通过参数控制所生成核的稀疏程度,算法即使在待组合的核数量很大的情况下仍然能够快速收敛,且模型训练的时间复杂度仅是训练样本的线性函数。该工作大大减轻了核学习的算法复杂度,并能控制核的稀疏和与数据拟合的程度,有很重要的理论和应用价值。但该工作并不完全适用于大数据,特别是高速数据流,其原因是它并非一种增量更新算法,而是一种批处理的优化方法。此外,该方法是一种有监督的核学习方法,并不能处理无标记的数据样本,而在大数据流中数据样本的标记缺失十分常见,因此核学习器的无监督学习能力非常重要。
针对数据流学习和模型的增量更新问题,研究者们对在线学习进行了深入研究,其中值得关注的研究工作是Jin等[9]提出的在线核学习框架,他们系统地提出了在线多核学习问题理论及其算法。针对核函数和核学习器的增量更新问题,他们提出了使用确定和随机2种方法进行更新,其中随机更新需要结合一定的采样策略进行。他们的工作对于基本核函数较多的情况下是有效的,但仅在有监督学习中进行研究,即遇到一个新的样本,若当前模型分类正确,则不进行更新动作,否则按照一定的策略更新模型。该方法并不直接适用于大数据流环境下的多核学习问题,其主要问题是它不能适应数据流产生规律变化的情况,且当某些数据缺少标签时模型无法有效处理。
本文认为要解决此问题需要同时考虑数据标签和数据的空间分布,使用增量学习的方法同步更新模型,这也是在当前很多大数据学习算法中所采用的策略。如Qin等[10]提出了一种适用于云计算增量梯度下降算法,解决大数据环境下带线性约束的凸优化问题。Yang等[2]提出了决策树的增量学习近似算法,可以在没有历史训练数据的情况下通过在线学习的方式直接更新决策树模型。但这些工作均是直接针对学习器进行增量更新,其方法并不直接适用于本文的核函数学习问题。
2 面向大数据的多核学习算法首先形式化描述多核学习问题,然后再给出带有数据依赖的多核学习问题,并给出在线学习版本的算法。核学习所解决的问题是直接从训练数据集(有标记或无标记)中学习参数化或半参数化的核函数,使其能充分反映数据所蕴含的分布规律。给定一系列的训练样本DL={(xi, yi)|i=1, 2, …, n},其中xi为属性集,yi∈{-1, +1}为分类标记,给定一个包含m个基本核函数的集合Km={kj(·, ·):X×X→R, j=1, 2, …, m},学习一组非负权值u={u1, u2, …, um, ∑iui=1},使核学习器在测试集上的分类错误最小化。由于权值非负,根据核函数的性质可知,核函数的凸组合仍为一个有效的核函数。该问题可以形式化描述为
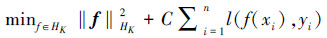 |
(1) |
式中:l为Hinge Loss损失函数,定义为l(a, b)=max(0, 1-ab),HK为核函数K所张成的希尔伯特空间,C控制模型复杂度与损失惩罚比重的参数。求解该优化问题的时间复杂度比较高,这是由于其中包含2步优化,第1步选择一个u,确定一个核函数
若通过限制基本核函数的个数或u中各分量的取值范围,则会牺牲多核学习的优势,且没有从根本上解决多核学习的问题。可以认为,在没有更好的求解算法的情况下,在线学习对上述问题是一种较好的求解策略。
2.1 在线多核学习为了进行在线学习,需要重新考虑式(1)。Jin等[9]的工作表明,当所学习的核函数为某个基本核函数集合的线性组合时,式(1)的最优化问题可以转化为如下问题:先求出每个核函数ki在各自张成的希尔伯特空间Hki上最优的fi,然后寻找一组权值u,使这些fi的组合最优,在寻找最优的过程中同步更新权值和fi。换句话说,若核函数的组合为线性时,在线多核学习问题可以两步求解,先使用基础的训练集为每一个核函数训练一个学习器,之后使用这些学习器进行在线学习,每读入一个训练样本时,根据当前的加权组合学习器对当前训练样本的输出结果,使用一种策略更新该核函数的权值和所对应的单个学习器,则最优的核函数为各个核函数使用该最优权值的加权组合体。即式(1)可以转化为以下问题:
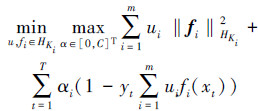 |
(2) |
图 1描述了上述求解过程的主要步骤。

|
| 图 1 多核在线学习算法的主要框架 Fig. 1 The main framework of online multiple kernel learning |
对式(2)进行分析可知,由于各个fi之间没有关联,因此fi的最优值可以单独求出,再用类似感知器的权值更新算法求解最优的组合权值u。由Representer定理可知,使式(2)最优的fi必定满足
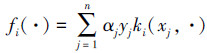 |
(3) |
式(3)给出了一种在线学习fi的方法,当读入一个训练样本时,先判断fi能否给出正确的标签,然后采用fi=fi+φyxki(x, ·)更新,其中φ为指示函数,当fi对x正确分类时其值为1,反之为0。Jin等在文献[9]中实现了上述思想。算法1描述了整个过程。
算法1 在线多核学习
输入:
核函数集合:Km={k1, k2, …, km}
初始化学习器:F={f1, f2, …, fm}
更新因子:β∈(0, 1)
最大分类错误的容忍水平:e
当前的权重向量:u
有标记数据样本:(x, y)
输出:更新后的权重u
1)y*=sign(wT·F(x))
2)if y*=y then
3)φ=0
4)else
5)φ=1
6)end if
7)for i=1, 2, …, m do
8)p=φ(min(e, -yfiT(x)+0.5))
9)ui=uiβp //更新u
10)fi=fi+φyki(x, ·)
11)end for
12)return u
算法1在输入有标记数据样本时,同时更新核权重和每个核所对应的学习器。当样本被当前学习器分类正确时,φ为0,此时不执行更新动作;若分类错误,则减少该学习器的权重,见算法1的第8)和第9)行。第10)行根据Representer定理对每个核所对应的最优学习器进行调整。最大错误容忍水平e控制以多大的力度去惩罚被学习器错分的样本。
由于仅对训练数据集进行一次扫描,算法1并不能达到离线批处理学习器的性能。但可依据感知器训练过程对算法1的收敛性分析如下。算法第10)行对各个fi进行更新,且各个fi相互独立,相当于m个独立的感知器训练过程,当输入样本线性可分时,各个fi可以收敛于当前训练集下的最优学习器,进而确定其最优组合;当输入样本线性不可分时,其收敛性依赖于各个学习器的核函数,一般情况下并不收敛于最优解,但实验部分的第4组实验说明经过一段时间后学习器的性能会趋于稳定,逼近一个可接受的较优解。
2.2 基于数据依赖的核函数修改数据依赖核[11]是一种无监督的核函数学习方法,实质是对核函数在训练样本集上的值进行修改,使其所反映的在可见数据样本上的距离更加符合数据样本点的空间分布,而不考虑样本标签。它可以对任意现有核函数根据可见的数据样本进行修改,实质是对由核函数所诱导的希尔伯特空间的内积进行修改[12]。首先给出数据依赖核的主要结论,然后再提出针对大数据和高速数据流的数据依赖核在线核学习算法。
给定一个核函数k和一个数据集D={x1, x2, …, xn},记kxi=(k(xi, x1), …, k(xi, xn)),M=(∑iWij-W)p,k关于D的Gram矩阵记为kD,Wij=RBF(xi, xj),xi, xj∈D。则可以通过式(4)的方式对核函数k进行修改,使其等距线沿D进行分布:
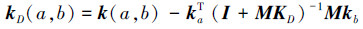 |
(4) |
其中a和b为任意2个训练样本,Μ是一个在原点对称的距离矩阵,按文献[12]的方法用图拉普拉斯矩阵计算得到。整个过程中并没有考虑数据的标签,仅是通过考虑数据的密度分布,对原有核函数的值进行修改。
式(4)的计算需要离线批量进行,且计算的时间复杂度较高,具体而言,式(4)在修改数据样本a和b的核函数值时要计算ka和kb,即a和b与当前可见数据集的核函数k值。当可见数据不变时,M和kD这两项只需计算一次,但对数据流而言,M和kD是在不断变化的。但可以肯定的一点是,对于大规模数据集和数据流,直接计算整个数据集的M和kD在计算资源上并不现实。
因此考虑M和kD的在线更新策略,采用限制M和kD的规模为N×N,则必须有D中的数据样本替换策略。借鉴操作系统中内存页面的调度算法,对静态的大数据集应用类似近期最少使用(least recently used, LRU)的样本更新策略[13],而对于高速数据流应用先进先出(first in first out, FIFO)更新策略[13],其中LRU是替换最近一段时间没有被使用过的样本,由于样本各不相同,本文采用聚类意义下的样本使用统计。这两种策略的合理性基于以下分析。对于静态大数据集,虽然数据是顺序地输入到学习器中,但其数据到达顺序和时序不相关,因此不能使用与时间密切相关的FIFO策略,而采用LRU策略较为合理;对于数据流,其数据生成规律有可能随时间变化而变化,因此替换存在时间最长样本的FIFO策略是合理的。同时,数据依赖核是通过对数据的分布估计对核函数进行修改,计算这种分布需要对一定规模的数据点进行分析,因此维持一个工作集M是必须的,它可被看作一个缓存,反映近一段时间的数据分布规律。这种限制工作集大小的更新策略有一定的局部性,但在有限的计算和存储资源下是折衷的策略。
算法维持一个不考虑标签的样本集D并进行在线更新。ka和kb的计算步聚是先查表kD,若不命中再计算,时间复杂度为O(N)。对于M和kD,替换样本之后需要重新计算一行,然后更新一行和一列,因此其时间复杂度也为O(N)。算法初始时计算M和kD的时间复杂度为O(N2)。
一个重要问题是LRU和FIFO中对输入样本的时间属性记录,对LRU还有聚类意义下最近被使用样本的判断。本文首先用聚类的方式产生数据集D的r个簇,应用在线聚类的方式更新这r个簇,替换样本时每次从最久没有被更新过的簇中随机选取一个样本进行替换,使用一个长度为r优先队列记录每个簇最近被访问的情况。对于FIFO策略,不需要优先队列,每次把新加入的样本放在最下行和最右列,然后去掉第1行第1列即可。算法2和算法3分别描述了静态大数据集和流数据集2种情况下的数据依赖核的在线学习过程。
算法2使用一个优先队列记录样本簇最近被访问的情况,认为一个簇中的样本被访问过一次,则该簇最近被访问过,核矩阵的更新从第7至10行,需要对所有样本扫描一次,时间复杂度是O(N2),优先队列的操作需要O(r),其中r为簇的个数,判断x0属于哪个簇的粗糙算法需要O(r)时间,整体的时间复杂度为O(N2)。
算法2 大数据集的数据依赖核在线学习
输入:
数据样本集: D={x1, x2, …, xN}
当前输入样本: x0
核函数Gram矩阵和距离矩阵: K、Μ
样本空间聚类分布: LC
记录簇最近访问的优先队列: Q
输出:更新后的核矩阵: K
1) r=clus(LC, x0) //查找样本x0的簇号
2)根据r更新优先队列Q
3)把x0加到簇r中
4)在优先队列Q的队尾所示的簇中随机去掉一个样本
5)初始化kx0
6)令k1=(k(x0, x1), …, k(x0, xN))
7) for j=1, …, N do
8)k2=K(j, ·)
9)kk0=k1-k1T(I+ΜK)-1Μk2
10)end for
11)用kx0更新矩阵K中关于x0的一行和一列
12) return K
算法3 流数据集的数据依赖核在线学习
输入:
数据样本集D={x1, …xN}
当前输入样本:x0
核函数Gram矩阵和距离矩阵: K、Μ
输出:更新后的核矩阵K
1)初始化kx0
2)k1=(k(x0, x1), …, k(x0, xN))
3)for j=1, …, N do
4)k2=K(j, ·)
5)kx0=k1-k1T(I+MK)-1Mk2
6)end for
7)用kx0更新矩阵K中的最后一行和最后一列
8)return K
对于数据流在线核学习问题,采用FIFO策略,即每次把当前的数据样本替换时间最长的数据样本,因此算法3中不需要优先队列。
算法4 半监督在线多核学习SSL-MKL
输入:
初始训练数据集D0输入数据样本集, D={xi, yi},xi是样本,yi是其标签
输出:更新后的核矩阵K
1)初始化K
2)使用批处理算法由D0学习K
3)for each (xi, yi) in D
4)if Li is not NULL then
5)Call算法1(xi, yi)
6)更新K
7)end if
8)if静态大数据集then
9)Call算法2(K, D0, M, xi, LC, Q)
10)else if数据流then
11)Call算法3(K, D0, M, xi)
12)end if
13)更新K
14)end for
15)return K
为了把在线多核学习和数据依赖进行结合,算法每读入一个数据样本x,判断是否有标签,若有标签,则先执行多核学习的权重值更新,再执行基于数据依赖的核修改;若没有标签,则仅执行核修改(算法2和算法3)。核修改是针对加权之后的核函数进行。算法4描述了2部分核学习的结合过程。
3 实验结果及分析在人工数据集和大数据学习的基准数据集上对本文算法进行有效性评估,并与现有的算法进行比较。人工数据集使用MOA[14]的序列生成器自动生成,在实验中共生成了3个规模不同的人工数据集,由MOA所生成的人工数据集被广泛用于大数据算法有效性的评估工作中[15-16]。基准数据集采用UCI数据集[19]中的数据集。实验中选取MOA提供的其中3个生成器生成不同的人工数据集,蕴含不同的数据生成规律。表 1和2分别展示了人工数据集和UCI基准数据集的主要信息。MOA序列生成器生成的3个人工数据集,以数据记录生成时间顺序保存在3个单独的数据文件中,在线多核学习时顺序读取文件中的数据进行训练和测试。2个UCI数据集中的数据随机重排之后按顺序读入。其中数据集M1生成20份,规模从106~2×107,用于评估数据集规模与CPU处理时间的增长关系。
| 编号 | 生成器类型 | 大小 | 属性个数 |
| M1 | WaveForm | 106~2×107 | 21 |
| M2 | RandomRBF | 106 | 37 |
| M3 | SEA Concepts | 106 | 25 |
| 编号 | 数据集描述 | 大小 | 属性个数 |
| M4 | Forest CoverType | 581012 | 54 |
| M5 | Poker-Hand | 107 | 11 |
在上述5个数据集上进行3组实验。第1组实验评估本文的半监督在线多核学习算法(semi-supervised learning-multiple kernel learning, SSL-MKL)的有效性,并与文献[17]中的批处理多核学习算法及文献[9]、[18]中的有监督在线多核学习算法进行比较。第2组实验分析本文算法对不同规模数据集处理的CPU运算时间增长与数据集大小之间的关系。第3组实验评估本文算法的迭代次数与学习器性能的变化关系,从而说明其收敛性能。
在3组实验中均采用参数随机的RBF核、多项式核和三角函数核函数各100个,即m=300。第1组实验采用如下设置:对比的一般核函数采用参数随机的RBF核和多项式核,核学习器使用标准的SVM,只进行二类分类,并采用0-1损失函数评估分类错误率。其中数据集M1的规模为106。在Μ和kD的更新算法中,限制其规模N为1000个样本。
第1组实验评估SSL-MKL算法有效性并与有监督的在线核学习算法进行比较,同时引入一个非在线学习的多核学习算法作为算法有效性的基线。表 3给出了对比算法的基本信息。
| 编号 | 参考文献 | 数据集 | 描述 |
| F1 | [17] | 全部 | 采用感知器与Hedge算法融合的在线核学习算法,优化过程采用随机梯度下降法 |
| F2 | [9] | 全部 | 在线多核学习算法,其基本原理同算法1,但权重更新策略不同 |
| F3 | [18] | M4、M5 | 批处理多核学习算法 |
F1与F2可以在5个实验数据集上运行,F3不能运行在数据流集上,即只能在M4和M5上运行,因此可以把M1、M2、M3与M4、M5分别进行比较。
由于算法F3无法直接处理M4和M5这样大规模的数据集,只能采用随机抽样的方法,限制训练集的大小才可以使用批处理算法。本组实验对训练数据集进行无回放抽样,抽样规模为10000。其余2个算法也在此抽样数据集上进行性能测试,对本文的SSL-MKL算法,从测试数据集中抽取同样规模的数据集作为算法的无标记数据。考虑到抽样的随机性,对批处理核学习进行10次抽样训练并记录10次的分类正确率的平均值。图 2展示了在M4和M5上的实验结果。

|
| 图 2 M4和M5的实验结果(限制数据集规模) Fig. 2 The main framework of online multiple kernel learning |
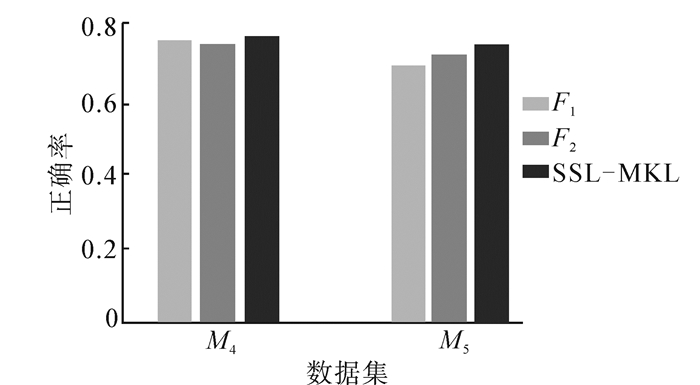
从图 2中可以看到,SSL-MKL不比F3差太多,但比F1和F2好,表明SSL-MKL对于规模受限制的数据集的性能较有监督的在线核学习算法(F1和F2)好,归功于SSL-MKL算法中的无监督学习对最终学习器性能提升的贡献,说明整个半监督学习框架的有效性。另一方面,注意到3个在线算法的性能均不如批处理算法F3,这是可以理解的,因为在线学习算法每次仅能“看到”当前的训练样本,且基本上不存储(SSL-MKL算法中的工作集仅是有限度存储),批处理方法在整个训练期间能访问所有的训练数据。因此可以接受在线学习方法性能稍差于批处理方法。但批处理方法难以处理大规模的数据集,正如本组实验的第2部分即将展示的(图 3),这正是在线学习方法的优势[20-21]。下面给出F1、F2与SSL-MKL在M4和M5整个数据集上的结果。训练集与测试集的规模按原数据集大小的3:7,对于SSL-MKL采用转导学习的方式[22-23],即把整个测试集作为无标记集。同样对数据集进行10次随机划分,记录每次分类正确率并计算方差,图 3给出了在数据集M4和M5上算法正确率的比较结果。
|
| 图 3 M4和M5的实验结果(完整数据集) Fig. 3 Evaluation results of M4 and M5 (full data set size) |
从图 3中可看出,由于有完整的训练集,各个算法的正确率相比图 2有所提升。SSL-MKL算法相比F1和F2的提升幅度比限制规模数据集时更大,表明数据依赖核对于数据分布的估计能够提升核函数的性能。
最后给出数据流集(M1、M2、M3)的测试结果。测试过程是把训练样本按其顺序号依次输入学习模型进行训练;在接受测试样本时,SSL-MKL同时进行无监督学习,而F1和F2,则仅输出测试结果。由于数据集有顺序,截取前面的30%作为训练集,后面70%作为测试集。表 4给出了实验中各算法在数据集上正确率的比较。
| M1 | M2 | M3 | |
| F1 | 0.731 | 0.788 | 0.775 |
| F2 | 0.742 | 0.781 | 0.770 |
| SSL-MKL | 0.768 | 0.796 | 0.802 |
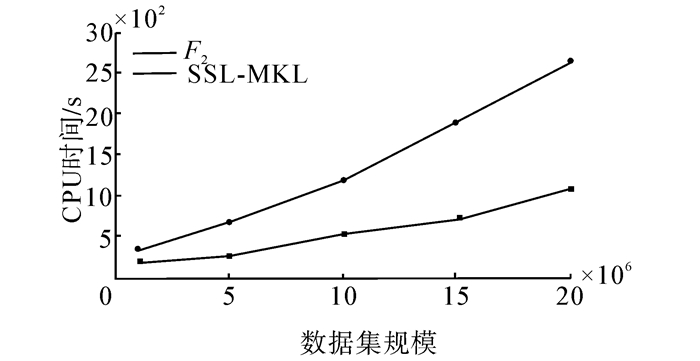
从表 4中可知SSL-MKL算法在3个数据集上都有最好的表现。第2组实验分析本文算法对不同规模数据集处理的CPU运算时间增长与数据集大小之间的关系。为了精确控制实验数据集的规模,本组实验使用了20种规模依次等距递增的M1数据集(以106为递增单位),记录了F2和SSL-MKL算法的核学习时间,图 4给出了运行时间对比。
|
| 图 4 不同数据集规模下的算法运行时间比较 Fig. 4 CPU Time comparison for different data set sizes |
从图 4中可以看出,SSL-MKL算法的运算时间与数据集的规模成线性关系,并且SSL-MKL算法的有监督学习部分的复杂性与算法F2同阶,从图 4中可以看出其运算时间的增长率与数据集规模有较好的线性关系,具有较好的可扩展性,能适用于更大规模的数据集的分析和应用问题。
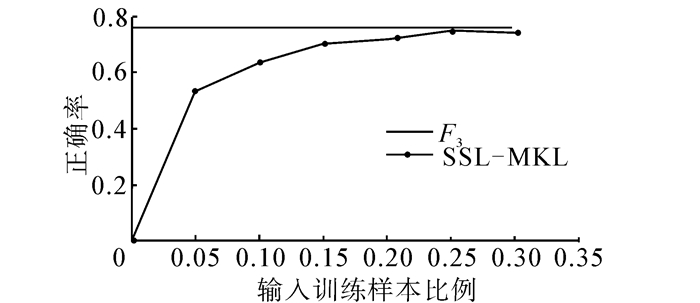
第3组实验评估算法SSL-MKL的迭代次数与学习器性能的变化关系,从而说明其收敛性。设置测试集为整个数据集的5%,通过随机有回放抽取的方式生成。训练集为整个数据集的30%,与第1组实验相同。每输入5%的训练数据,运行一次测试并记录结果。上述过程重复10次取平均正确率。并以F3在限制数据集规模的实验(第1组)中的正确率作为基线进行对比。图 5给出了在M4数据集上算法正确率迭代收敛性的实验结果。
|
| 图 5 算法正确率的收敛性 Fig. 5 The convergence of accuracy of the proposed algorithm |
在图 5中,F3表示离线批处理核学习方法得到的核函数在SVM上的测试正确率曲线,SSL-MKL代表本文方法。每输入一个样本算法1就会运行一次,核函数同时更新一次。从图 5中可以看出,在开始阶段,仅需读入少量样本(5%),SSL-MKL的正确率会大幅上升,随后会比较稳定收敛于一个较优的值。当输入数据的内在生成规律相对稳定时,SSL-MKL对核函数的更新会在一段时间内(如图 5中输入15%数据之后)稳定下来,从而产生较稳定的测试结果。
4 结束语大数据环境下的多核学习问题是大数据机器学习的一个基础性问题,比单纯通过改进训练算法效率构建学习器有更重要的意义。本文提出了一种适用于大数据环境下的在线多核学习算法,考虑了数据的有监督信息以及数据的空间分布,并应用数据依赖核的构建方法,对所学习得到的核函数进行无监督修正,使其具有更好的泛化能力。算法基于在线学习的框架进行增量学习,仅需对训练数据进行一次扫描,就可以更新核函数,并不需要对历史数据进行保存。算法适用于高速数据流,以及训练数据规模很大以致不能全部加载到内存中的情形。在由著名的大数据流分析工具MOA生成的人工数据集和UCI的大数据集上进行算法有效性评估,表明了本文方法能学习得到与数据集规律相一致的核函数,在分类器上有较好的效果,且本文算法是一种在线学习算法,支持数据增量更新。此外,本文的算法能同时处理有标记和无标记数据,对于数据概念标记稀疏的高速数据流可以进行半监督学习,有很好的扩展性。
| [1] | GOPALKRISHNAN V, STEIER D, LEWIS H, et al. Big data, big business: bridging the gap[C]//Proceedings of the 1st International Workshop on Big Data, Streams and Heterogeneous Source Mining: Algorithms, Systems, Programming Models and Applications. Beijing, China, 2012: 7-11. |
| [2] | YANG H, FONG S. Incrementally optimized decision tree for noisy big data[C]//Proceedings of the 1st International Workshop on Big Data, Streams and Heterogeneous Source Mining: Algorithms, Systems, Programming Models and Applications. Beijing, China, 2012: 36-44. |
| [3] | JORDAN M I. Divide-and-conquer and statistical inference for big data[C]//Proceedings of the 18th ACM SIGKDD international conference on Knowledge discovery and data mining. Beijing, China, 2012: 4-4. |
| [4] | ACAR U A, CHEN Y. Streaming big data with self-adjusting computation[C]//Proceedings of the 2013 Proceedings of the 2013 Workshop on Data driven Functional Programming. Rome, Italy, 2013: 15-18. |
| [5] | ARI I, CELEBI O F, OLMEZOGULLARI E. Data stream analytics and mining in the cloud[C]//Proceedings of the 2012 IEEE 4th International Conference on Cloud Computing Technology and Science. Washington, DC, USA, 2012: 857-862. |
| [6] | AGMON S. The relaxation method for linear inequalities[J]. Canadian Journal of Mathematics , 1954, 6 (3) : 393-404 |
| [7] | GONEN M, ALPAYD E. Multiple kernel learning algorithms[J]. Journal of Machine Learning Research , 2011 (12) : 2211-2268 |
| [8] | ORABONA F, JIE L, CAPUTO B. Multi kernel learning with online-batch optimization[J]. Journal of Machine Learning Research , 2012 (13) : 227-253 |
| [9] | JIN R, HOI S C H, YANG T, et al. Online multiple kernel learning: algorithms and mistake bounds[J]. Algorithmic Learning Theory , 2010 (6331) : 390-404 |
| [10] | QIN C, RUSU F. Scalable I/O-bound parallel incremental gradient descent for big data analytics in GLADE[C]//Proceedings of the Second Workshop on Data Analytics in the Cloud. New York, USA, 2013: 16-20. |
| [11] | SINDHWANI V, NIYOGI P, BELKIN M. Beyond the point cloud: from transductive to semi-supervised learning[C]//Proceedings of the 22nd International Conference on Machine Learning. Bonn, Germany, 2005: 824-831. |
| [12] | 李宏伟, 刘扬, 卢汉清, 等. 结合半监督核的高斯过程分[J]. 自动化学报 , 2009, 35 (7) : 888-895 LI Hongwei, LIU Yang, LU Hanqing, et al. Gaussian processes classification combined with semi-supervised kernels[J]. Acta Automatica Sinica , 2009, 35 (7) : 888-895 DOI:10.3724/SP.J.1004.2009.00888 |
| [13] | 邹恒明. 计算机的心智:操作系统之哲学原理[M]. 北京: 机械工业出版社, 2012 : 100 -102. |
| [14] | BIFET A, HOLMES G, KIRKBY R, et al. MOA: massive online analysis[J]. Journal of Machine Learning Research , 2010 (11) : 1601-1604 |
| [15] | KREMER H, KRANEN P, JANSEN T, et al. An effective evaluation measure for clustering on evolving data streams[C]//Proceedings of the 17th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining. San Diego, California, USA, 2011: 868-876. |
| [16] | BIFET A, HOLMES G, PFAHRINGER B, et al. Mining frequent closed graphs on evolving data streams[C]//Proceedings of the 17th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining. San Diego, USA, 2011: 591-599. |
| [17] | FRANCESCO O, LUO Jie, BARBARA C. Multi kernel learning with online-batch optimization[J]. Journal of Machine Learning Research , 2012 (13) : 227-253 |
| [18] | STEVEN C H, RONG Jin, ZHAO Peilin, et al. Online multiple kernel classification[J]. Machine Learning , 2013, 90 (2) : 289-316 DOI:10.1007/s10994-012-5319-2 |
| [19] | UCI数据集: http://archive.ics.uci.edu/ml/[EB/OL].[2014-03-18]. |
| [20] | YANG Haiqin, MICHAEL R L, IRWIN K. Efficient online learning for multitask feature selection[J]. ACM Transactions on Knowledge Discovery from Data , 2013, 7 (2) : 6-27 |
| [21] | CHEN Jianhui, LIU Ji, YE Jieping. Learning incoherent sparse and low-rank patterns from multiple tasks[J]. ACM Transactions on Knowledge Discovery from Data , 2012, 5 (4) : 22-31 |
| [22] | HONG Chaoqun, ZHU Jianke. Hypergraph-based multi-example ranking with sparse representation for transductive learning image retrieval[J]. Neurocomputing , 2013 (101) : 94-103 |
| [23] | YU Jun, BIAN Wei, SONG Mingli, et al. Graph based transductive learning for cartoon correspondence construction[J]. Neurocomputing , 2012 (79) : 105-114 |



