2. 军事科学院 运筹所,北京 100091
2. Institute of Military Operation Research of the Academy, Military Science, Beijing 100091, China
如何有效分析和选择打击具有复杂关联的目标,是军事决策中的关键问题。目标间的复杂关联可以用目标体系(target system of system, TSoS)来描述。目标体系是由多个作战系统构成的集合,每个作战系统实现自身任务,并对体系的使命产生影响[1]。每个作战系统又是由多个作战单元间关联构成的集合。由于目标体系的层次结构,对作战单元打击会引起目标系统直至体系的失效。
目前对目标体系打击的研究主要是采用贝叶斯网络(Bayesian network, BN)[2]、影响网[3]、影响图[4]等概率网络方法分析目标体系薄弱点,以求解目标打击行动序列或者目标集,但由于目标体系内部关联的复杂性,这些方法需要输入大量条件概率,并且对网络拓扑和概率知识重用性较差。有些文献使用图论[5]或故障树方法[6-7]描述目标毁伤对目标体系失效的影响,但未考虑行动结果的不确定性。
为处理目标体系中影响关系的复杂性,文中使用面向对象贝叶斯网络[8](object-oriented Bayesian network,OOBN)分析目标体系层次间失效影响的拓扑结构,建立打击目标体系效果分析模型,在此基础上给出了关键目标选择方法,并举例说明了建模和求解的过程。
1 目标体系结构描述和典型影响关系由目标体系定义可知,目标体系可被层层分解为目标系统、目标单元。
目标单元是组成目标体系的最小元素,其状态为正常、摧毁;目标系统是由多个目标单元组成的提供独立功能的集合,其能力状态受到目标单元状态影响,划分为运行、失效2种状态;目标体系是由多个目标系统组成的完成某个使命任务的集合,其能力状态受到包含的目标系统能力状态的影响,按照是否具备完成使命能力被划分为运行、失效。
目标体系在遭受打击后,目标状态间会体现以下3种典型关系:层次失效影响关系、共同毁伤关系、响应关系。
1)层次失效影响关系
根据目标体系层次,目标单元的失效会引起其他目标或者上层目标系统的失效,目标系统的失效可能引起其他目标系统或者整个目标体系的失效。
2)共同毁伤关系
由于目标单元间在空间(地理空间、电磁空间等)上的邻近关系,当对某一目标单元打击时,会同时对多个目标单元造成附带毁伤,例如对桥梁进行摧毁,可同时摧毁通过桥梁上的通信、电力线路。
3)响应关系
敌方目标体系还存在响应关系,为提高目标体系生存能力,目标单元可能具有备份目标或者接替目标,当目标单元毁伤时,敌方进行响应,使用这些目标备份或者接替该毁伤目标,使得目标体系继续运转完成任务。
2 打击目标体系效果分析模型建立打击目标体系效果分析模型,分析目标体系层次间的影响关系,是选择关键行动集的前提。BN能较好描述这种复杂影响关系[1-3],但普通贝叶斯网络需要获取大量的条件概率表,建模复杂度随着目标和关联数量增加而不断加大。本文采用OOBN[8]方法简化BN的建立过程。OOBN[8]采用面向对象思想,OOBN中的类是一个BN片断,其内部可能包含其他类实例。OOBN利用小的片断构建复杂系统模型,降低了对于复杂系统建立BN模型的复杂性和难度。
2.1 打击目标体系效果分析建模的基本步骤使用OOBN描述打击目标体系的效果分析模型的基本步骤为:1)分析目标体系各层元素间、行动与目标单元间的影响关系,建立目标体系层次失效影响的实体关系图;2)分析对象内部影响关系的BN片段,创建对应的类、类实例化,建立目标体系层次失效影响OOBN;3)进行概率推理,分析打击行动造成的目标体系层次失效影响效果。
2.2 目标体系层次间失效影响的实体关系图为分析对目标体系的打击效果,需明确目标体系层次失效影响的过程。首先,当对目标实施打击时,目标运行模式不同,摧毁概率不同,例如打击在行进状态下和在隐蔽状态下车辆的成功概率存在不同;其次,目标单元毁伤引起目标系统能力的失效,进而引起上一层目标系统能力的失效,直至影响目标体系能力的失效。实体关系如图 1所示。
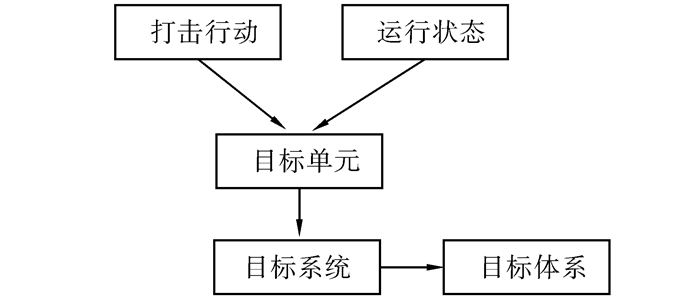
|
| 图 1 目标体系层次失效影响的实体关系 Fig. 1 Entity relations graph of failure influences among target levels of TSoS |
按照BN片断的影响层次关系,可分为行动对目标单元的影响片断、目标单元对目标系统的影响片断、目标系统对目标系统(体系)的影响片断。
细化每一个片断输入、输出节点,确定BN拓扑结构和每个节点的条件概率表,为OOBN的建立奠定基础[9]。设Di为打击行动,Ti为目标单元节点,Ri为目标单元运行模式,Ci为目标单元能力,Mi为目标系统节点,Ei为目标系统能力,Si为目标体系能力。用正方形表示决策节点,如打击行动等;长方形表示目标系统的类,如目标系统、目标单元等;圆圈表示随机节点,如目标单元运行状态;虚线圆圈或正方形表示输入节点,实线圆圈表示输出节点。
2.3.1 行动对目标单元的影响片断设输入节点为:打击行动Di,目标运行模式Ri;输出节点为:目标单元能力Ci。行动对目标单元的影响片断图如图 2所示。

|
| 图 2 行动对目标单元影响片断 Fig. 2 The fragment of the influence action exerts upon target unit |
设有2种目标运行模式W1、W2,其初始分布概率分别为P0、1-P0。行动对目标单元影响的条件概率如表 1所示。
| Di | Ri | Ci | |
| true | false | ||
| true | W1 | P1 | 1-P1 |
| true | W2 | P2 | 1-P2 |
| false | — | 1 | 0 |
在打击中存在共同毁伤,即同一打击行动会引起多个目标单元毁伤,在OOBN中描述为由一个打击行动节点指向多个目标单元能力节点。如图 3所示,打击行动Di影响了目标单元Ti和Tj。
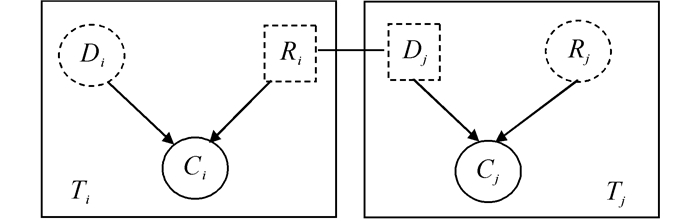
|
| 图 3 打击行动对目标单元影响片断(共同毁伤) Fig. 3 The fragment of the influence action exerts upon target units (common damage) |
设输入节点为:目标单元能力Ci、Cj,输出节点为:目标系统能力Ei。目标单元对目标系统的影响片断如图 4所示。
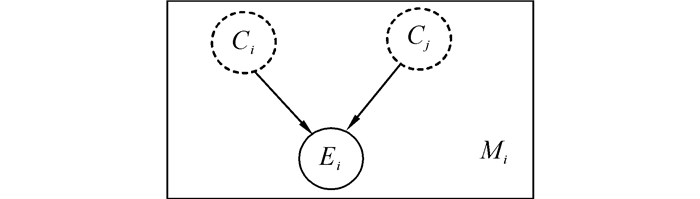
|
| 图 4 目标单元对目标系统的影响片断 Fig. 4 The fragment of the influence target units exert upon system |
如果目标之间是备份或者接替关系,则目标状态之间是上下文独立关系,上下文独立关系[10]是指贝叶斯网络中某些状态变量取特定值后,其余状态变量间存在的独立关系。当主目标未被毁伤时,目标系统的状态只与主目标产生关联,在主目标被毁伤时,目标系统状态只与备份(接替)目标的状态相关。设Ti是主目标,Tj是备份或者接替目标,对应条件概率如表 2所示。
| Ti | Tj | Ei | |
| true | false | ||
| true | — | 1 | 0 |
| alse | true | P1 | 1-P1 |
| false | false | 0 | 1 |
2.3.3 目标系统对目标系统(体系)的影响片断
设输入节点为:目标系统能力Ei、Ej,输出节点为:目标系统Mk的能力节点Ek或目标体系的能力节点S。如图 5所示。
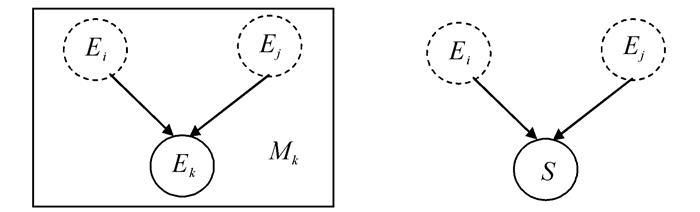
|
| 图 5 目标系统对目标系统(体系)影响片断 Fig. 5 The fragment of the influence target systems exert upon target system (TSoS) |
根据目标系统的包含关系,被包含目标系统的能力节点指向上层目标系统的能力节点,再由目标系统能力节点指向目标体系能力节点。
2.4 目标体系层次失效影响关系的OOBN图根据各片断的输入、输出节点和目标体系、目标系统、目标单元的层次影响关系,将各种片断组织起来,构成目标体系的完整OOBN,如图 6所示。
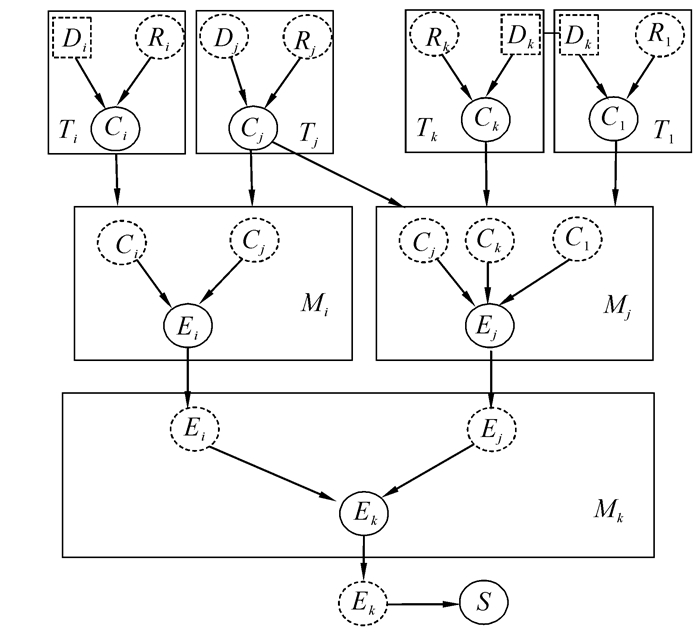
|
| 图 6 目标体系层次失效影响OOBN拓扑结构 Fig. 6 The structure of the failure influence in TSoS |
图 6刻画了打击行动与目标单元状态间的相关性、目标体系不同层次能力的失效影响特性。用表示关联性的有向弧链接各节点,构成整个模型。
在对OOBN进行推理时,将其按照文献[11]中的算法将其先转化为普通的BN,再实施BN推理。
2.5 目标间响应关系的条件概率计算方法当目标单元与目标系统间、目标系统与目标系统(体系)间的关系类型是逻辑“与”、“或”、“N中取K”关系,能够直接转化为目标对目标系统的概率影响关系,文献[6]中给出了各类逻辑影响关系到贝叶斯网络条件概率表的映射关系。
当目标单元之间是备份或者接替关系时,备选目标对主目标的备份成功概率难以直接给出,本文通过目标单元间属性相似度的方法来计算备选目标对主目标的备份成功概率。假设有目标Tj是目标Ti的备选目标,能够对Ti的功能进行接替或者备份,则判断每个目标与目标Ti属性的相似度Di, j,相似度越大的备选目标Tj,其备份目标Ti的能力就越大,相似度为1时,完全能够备份主目标运行。
假设目标单元Ni的属性取值为向量(a1, a2, …, ak, …, an), (1≤k≤K),备选目标中Nj的属性取值向量取值为(bj, 1, bj, 2, …, bj, k, …, bj, n)(1≤k≤K),在此给出相似度阈值:
DA=(D1, D2, …, Dk, …, DK), (1≤k≤K),认为当备选目标与主目标之间在第k个属性上的距离绝对值大于阈值Dk时,两者之间不会发生响应关联;例如时间紧迫度阈值DT,当备选目标接替或备份主目标所需响应时间T大于DT时,备份成功概率为0。
目标的属性分为2类:越大越优型和越小越优型,当属性为前者,rk=1;当属性为后者,rk=-1。不同目标在第k个属性上的距离值dk∈[0, 1],当备选目标属性值优于或等于主目标属性值时,dk=0;当两者之间距离值大于阈值时,两者不发生响应关联,dk=1。
 |
再计算备选目标对主目标的功能匹配度为两者属性的综合相似度,即为
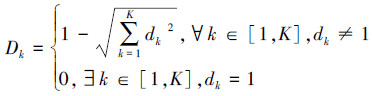 |
Dk即是备选目标备份主目标的成功概率。
3 深度优先关键行动选择启发式算法在实施对目标体系的打击时,需要以最小的代价达成使目标体系崩溃的目的。关键行动是指给定打击目标体系的失效程度指标(失效概率),所需要采取的最小行动集。
设打击目的是使得目标体系失效概率p≥PD,对应的关键行动集选择步骤:
1)从体系层次树自上而下进行深度搜索:
2)对于同一层次的节点,优先选择共享节点或共同毁伤节点;在分解到目标单元层时,优先选择摧毁概率最高的目标单元;
3)若兄弟节点是并联目标,加入这些节点,若兄弟节点是串联目标,则忽略;
4)自上而下重复2)至4),直至完全分解到目标单元层,从而得到一个最小打击目标集T,从T中删除重复的目标单元;
5)若T中的目标单元存在共同毁伤目标,则将能够共同毁伤的其他目标单元加入根据BN推理算法,计算T对应的目标体系失效概率p;
6)若p≥PD,输出T作为关键目标集,否则转7);
7)则对于余下目标集上划线T中的目标单元Ni,如果T中存在Ni的并联目标,则在T中加入Ni和其并联目标,计算对应的体系失效概率pi′,得到平均失效增幅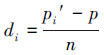
8)对于T中不存在并联节点的目标单元Ni,在T中加入Ni,计算对应的体系失效概率pi′,得到平均失效增幅di=pi′-p;
9)若pi′ < PD,则T加入失效增幅di最大的目标Ni,如果Ni存在并联目标,则也加入T。从T中删除加入T的目标。转到步骤7);
10)若pi′≥PD,输出T作为关键目标集。
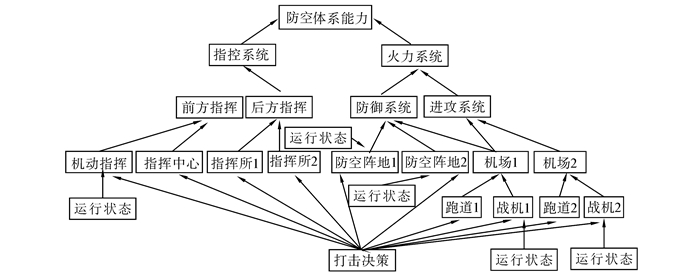
4 分析与验证文中以典型的防空目标体系为例说明该方法的使用。案例中的防空体系可分解为指控系统、火力系统,之间为逻辑与关系;指控系统分解为前方指挥系统和后方指挥系统,之间为逻辑与关系;前方指挥系统由指挥中心和机动指挥所实现,机动指挥所在指挥中心毁伤后从隐蔽进入运行状态进行备份,成功概率为0.8;后方指挥系统由指挥所1和指挥所2实现,之间为逻辑或关系;火力系统分为防御系统和进攻系统,之间为逻辑与关系;防御系统包括防空阵地1、2和机场1,逻辑关系为N中取K关系,若其中2个节点被摧毁,系统失效;进攻系统包括机场1、2,之间为逻辑或关系;机场1、2都可被分解为跑道和机群,之间为逻辑与关系。指挥所2和防空阵地1属于共同毁伤节点,机场1是防御系统和进攻系统的共享节点。
在不同目标状态下打击行动的成功概率如表 3所示。首先分析得到目标体系层次失效影响对应的对象关系,如图 7所示。根据实体关系图,建立OOBN,并根据文献[11]的方法,将其转化为普通贝叶斯网络,如图 8所示,用GENIE[12]绘制,对于只有一种运行状态的目标,不再画出其运行模式节点。
| 打击目标 | 运行状态 | 成功概率 |
| 指挥中心 | 运行 | 0.6 |
| 机动指挥所 | 隐蔽 | 0.3 |
| 机动指挥所 | 运行 | 0.8 |
| 指挥所1 | 运行 | 0.5 |
| 指挥所2 | 运行 | 0.6 |
| 防空阵地1 | 隐蔽 | 0.3 |
| 防空阵地1 | 运行 | 0.6 |
| 防空阵地2 | 隐蔽 | 0.4 |
| 防空阵地2 | 运行 | 0.7 |
| 跑道1 | 运行 | 0.7 |
| 机群1 | 隐蔽 | 0.5 |
| 机群1 | 跑道 | 0.8 |
| 跑道2 | 运行 | 0.7 |
| 机群2 | 隐蔽 | 0.4 |
| 机群2 | 跑道 | 0.8 |
|
| 图 7 防空目标体系层次失效影响实体关系图 Fig. 7 The entity relation of the failure influence among the air force TSoS |
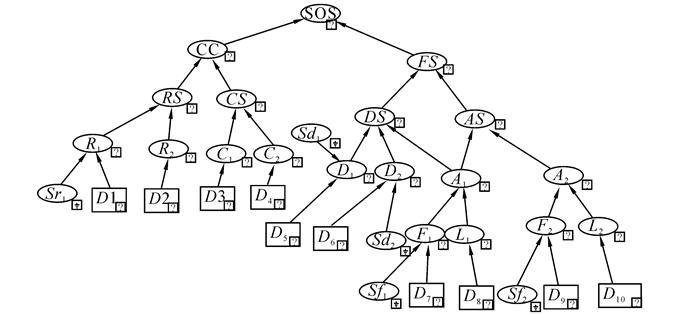
|
| 图 8 目标体系的贝叶斯网络 Fig. 8 Bayes network of TSoS |
已知各节点初始状态,除了机动指挥所、防空阵地1、机群2的运行状态为隐蔽,其他节点的状态均为运行。设目标体系的失效阈值为70%,即要使得目标体系的失效概率达到70%以上,求解所需要选择的最小行动集。
根据第2节的方法,得到打击集为打击机动指挥所、指挥中心、指挥所1、指挥所2、防御阵地2、机群1,在该打击集下目标体系的失效概率为77%。
设目标体系的失效阈值为80%,根据该方法求得的最小打击集为打击机动指挥所、指挥中心、指挥所1、指挥所2、防御阵地1、防御阵地2、机群1,在该打击集下,目标体系的失效概率为83%。
5 结束语文中基于目标体系结构和典型目标影响关系,使用OOBN建立了打击目标体系效果分析模型,给出了目标间影响关联的条件概率计算方法,并使用基于深度搜索的启发式算法求解关键打击行动。和以往研究相比,该建模方法能减少目标体系中影响关系的建模复杂性,增加重用性。通过典型的防空目标体系实验表明,所提出的模型和求解方法能为选择打击具有复杂关联关系的目标提供有效辅助。
| [1] | ZHOU Y, ZHU C, LEI T, et al. A COG analysis model of system-of-systems (SoS) based on multi-entity Bayesian networks[C]//The 13th International Conference on Artificial Intelligence. Las Vegas, Nevada, USA, 2011. |
| [2] | FALZON L. Using Bayesian network analysis to support centre of gravity analysis in military planning[J]. European Journal of Operational Research , 2006, 170 : 629-643 DOI:10.1016/j.ejor.2004.06.028 |
| [3] | KUTER U, NAU D, GOSSINK D, et al. Lemmer. Interactive course-of-action planning using causal models[C]//Proceedings of the Third International Conference on Knowledge Systems for Coalition Operations. Pensacola, USA, 2004: 1-12. |
| [4] | POUSI J. Decision analytical approach to effects-based operations[D]. Helsinki, Finland: Helsinki University of Technology, 2009: 35-63. https://core.ac.uk/display/21103516 |
| [5] | 秦前付, 曹存根, 徐洸. 基于图论的计划军事效果评估[J]. 计算机科学 , 2005, 32 (7) : 148-151 QIN Qianfu, CAO Cungen, XU Guang. Evaluating military effect of air operational plan based on network theory[J]. Computer Science , 2005, 32 (7) : 148-151 |
| [6] | 李新其, 向爱红, 李红霞. 系统目标毁伤效果评估问题研究[J]. 兵工学报 , 2008, 29 (1) : 57-61 LI Xinqi, XIANG Aihong, LI Hongxia. Calculation and assessment on damage effect of system target[J]. Acta Armamentarii , 2008, 29 (1) : 57-61 |
| [7] | 袁震宇, 谢春思, 张宇, 等. 基于故障树的系统目标打击决策模型研究[J]. 舰船电子工程 , 2010, 30 (7) : 52-55 YUAN Zhengyu , XIE Chunsi, ZHANG Yu, et al. Model study of system-target attacking decision based on fault tree[J]. Ship Electronic Engineering , 2010, 30 (7) : 52-55 |
| [8] | KOLLER D, PFEFFER A. Object-oriented Bayesian networks[C]//Proceedings of the Thirteenth Annual Conference on Uncertainty in Artificial Intelligence. Providence, Rhode Island, USA, 1997: 302-313. |
| [9] | 蒋国萍, 陈英武. 基于面向对象贝叶斯网络的软件项目风险评估[J]. 系统工程与电子技术 , 2005, 27 (2) : 353-356 JIANG Guoping, CHEN Yingwu. Software project risk evaluation method based on object-oriented Bayesian network[J]. Systems Engineering and Electronics , 2005, 27 (2) : 353-356 |
| [10] | 黄友平.贝叶斯网络研究[D].北京:中国科学院研究生院, 2005: 20-21. HUANG Youping.Research on Bayesian Network[D]. Beijing: University of Chinese Academy of Sciences, 2005: 20-21. http://cdmd.cnki.com.cn/Article/CDMD-80132-2006191403.htm |
| [11] | BANGS O, WUILLEMIN P H. Top-down construction and repetitive structures representation in Bayesian networks[C]//Proceedings of the Thirteenth International Florida Artificial Intelligence Research Society Conference. Orlando, Florida, USA, 2000: 282-286. |
| [12] | University of Pittsburgh Decision Systems Laboratory. Graphical Network Interface (GeNIe2.0) [EB/OL].Available: http://genie.sis.pitt.edu/. |



