边缘学习[1-5]是机器学习的核心问题之一。目前比较成功的边缘学习算法主要有V.Vapnik提出的SVM最大边缘算法[6-8], Fabio Ailli、Alessandro Sperduti提出的TVQ算法[9]和同调边缘胞腔学习算法等[10-11]。
支持向量机(support vector machine, SVM)是一种努力最小化结构风险[12-13]的算法,主要有线性可分支持向量机[12]、近似线性可分支持向量机[12]和线性不可分支持向量机。线性可分支持向量机又叫硬间隔支持向量机[12], 它是在正确划分训练集的超平面中,采用极大间隔分类超平面的方法[12, 14-15],根据最大间隔原则,找出最优的决策超平面。近似线性可分支持向量机即软间隔支持向量机(soft margin SVM)[15], 是在线性可分的情况下建立起来的,即在线性可分支持向量机的最优化问题上添加松弛因子ξi和惩罚因子C, 允许有错分样本存在。线性不可分[12, 15]是通过引入一个核函数[12]来实现的,该方法是将原始数据通过非线性映射投影到高维空间,使得数据在高维空间变得线性可分。
在TVQ算法中,提出了一个对提升边缘问题的很好的方案,该方案是建立在边缘理论原则上,是基于样本加权策略。其算法实例包含了基于1-NN分类器的切线距离[16],其中1-NN分类器加入了一种量子化的切距离原型。该算法中,引入的切距离原型在关于标准切线模式的泛化误差中得到了明显的改进。该方法与SVM方法进行比较,可以观察到,当此方法和SVM方法具有从经验风险到理想风险中一致收敛的统计学习理论概念时,该方法将输入分布直接工作在非线性模型上而不是采取预定义核的方式。该方法和Boosting算法[17-18]很相似,但是在Boosting算法中,采取的是多种组合假设;而在TVQ算法中,更加关注的是独立假设。
SVM和TVQ在一定程度上都提高了边缘划分效果和准确度。但是这些方法对边缘可变的划分问题就显得不足了,因此本文提出了一种邻域同调学习算法。邻域同调学习算法是通过引进同调论思想,从机器学习的角度出发研究的一种边缘学习新方法。该方法针对图集的分类问题,在分类过程中能够有效地保证图形的结构特征不变。该方法主要是通过判断给定图形的邻域复形的各阶同调群是否同构,对图形进行邻域同调分类。
1 邻域同调的基本概念同调[19-20]是源于代数拓扑学[21]的一个分支。20世纪40年代,代数拓扑学的一些概念和方法被引进春代数领域,形成了系统的理论,它的兴起对群、李代数[22]与结合环的研究都起了非常重要的作用。同调的研究对象基本上是模范畴[23-24]所派生一些Abel范畴,其核心是同调以及同调函子。代数拓扑学中的复形、同调群等概念也由此引入。其中起重要作用的一类模[23-24]是投射模、内射模和平坦模,利用它们定义了扩张函子和n级张量函子以及同调维数[24]等概念。在环论研究中,利用同调性质来刻画环自身结构取得了一系列重要成果。计算群、环、代数的同调群是同调的重要研究课题。
为了方便讨论,先介绍一些基本概念。
定义1 设点集{a0, a1, …, aq}⊂Rn,Rn表示线性的n维欧氏空间,若矢量组a1-a0, a2-a0, …, aq-a0线性无关,则称点集{a0, a1, …, aq}⊂Rn在Rn中是几何独立的。
设点集{a0, a1, …, aq}在Rn中几何独立,令
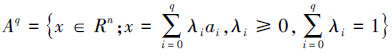 |
称Aq为q维几何单形,简称q维单形,记作〈a0, a1, …, aq〉,a0, a1, …, aq称为q维单形Aq的顶点,实数λi称为点x在q维单形Aq中的重心坐标。
定义2 设K=Aiq, q=0, 1, …, n, i=1, 2, …, αq是Rm中有限个单形的集合,若满足下列2个条件,则称K为单纯复形。
1)K中任意2个单形都是规则相处的;
2)K中任意单形的任意一个面仍是K中的单形。
单纯复形K中的0维单形称为K中的顶点。K的维数是K中单形维数的最大值,即dimK:=max{q; Aq∈K}。对于一个q维单形的全体顶点a0, a1, …, aq,它们的全部排列可以分成2组:同一组(如:同是顺时针方向)中的排列彼此差一个偶置换,不同组之间的排列,彼此差一个奇置换。这两组叫做Aq的2个定向。选定定向的单形叫做有向单形,那么可以将该有向单形中的一组记作+σq(简记作σq),另一组相反指向的记作-σq。
现有一n维单纯复形K,{Aiq; q=0, 1, …, n, i=1, 2, …, αq}是它的全部单形。对每个Aiq取定一个指向,这个有向单形记作σiq(另一个指向决定的有向单形就是-σiq)。则称{σiq; q=0, 1, …, n, i=1, 2, …, αq}为K的有向单形的一个基本组。
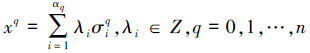 |
(1) |
叫做K的一个q维链。链(1)与同维链yq=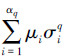
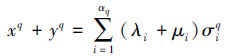 |
(2) |
显然,在式(2)的加法运算下,q维链的全体构成一个自由交换群,记作Cq(K),即
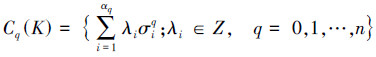 |
(3) |
Cq(K)叫作K的q维(整数)链群。且对于任意K的q维链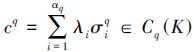
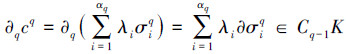 |
(4) |
则∂q:Cq(K)→Cq-1(K)是群同态。这里的∂q即为q维边缘算子或边缘同态。其实,边缘同态是几何上概念的代数化,是用来反映图形的边界关系的。
在此基础上,定义出一个单纯链复形C*(K)={Cq(K), ∂q}。C*(K)即是一串q维(整数)链群Cq(K)和一串边缘同态∂q:Cq(K)→Cq-1(K),排成一个序列:
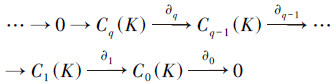 |
(5) |
满足条件对每个维数q都有∂q∂q+1=0,也就是说“2次边缘为零”。
定义3 单纯复形K的q维闭链群和边缘链群依次为
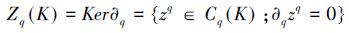 |
(6) |
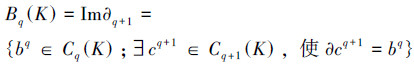 |
(7) |
Zq(K)的元zq叫做q维闭链,Bq(K)的元bq叫做q维边缘链。
这里Bq(K)⊂Zq(K),而且作为自由群Cq(K)的子群,它们也都是自由的。Zq(K)是描述有可能成为边的图形,Bq(K)是描述真的是边的图形。那么“有可能成为边,又不真是边”这一事实,用群论的语言来表达,就应该是:在有可能成为边的Zq(K)中,模真是边的部分Bq(K)。这样就有商群:
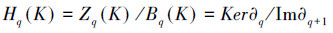 |
Hq(K)叫做单纯复形K的q维(单纯)同调群。
同调群Hq(K)中的元素为Zq(K)中元素的模Bq(K)的等价类,因此,由单纯复形K上q维闭链zq所决定的模Bq(K)的等价类是zq+Bq(K),记作[zq],称其为zq的q维同调类,并且Hq(K)={[zq]; zq∈Zq(K)}。同一同调类中的元z1q和z2q称为同调的,记作z1q~z2q或z1q-z2q~0。
由定义2可以看出单纯复形是由简单的图形——单形构成的。那么有了一个单纯复形之后,由此出发也可构成相应的新复形。其实仔细观察单纯复形的定义就会发现,单纯复形实际上完全由其顶点和顶点构成的子集组(单形)所决定,当然这时顶点的子集组要适合某种条件。据此,定义4给出了抽象复形的定义,该定义则为本文算法中提到的构造邻域复形提供了理论基础。
定义4 以有限个元素c0, c1, …, cq的子集做为元素所得的集K,叫做以c0, c1, …, cq为顶点的抽象复形,如果满足以下2个条件:
1)由单个元素ci所组成的子集属于K,这里i=0, 1, …, q;
2)若A是K的元,则A的子集也是K的元。
抽象复形K中的元A叫做抽象单形,它的维数是其顶点数减1。A的子集叫做A的面。K的维数是K中诸单形的最大维数。显然,每个单纯复形K都自然地决定一个抽象复形K。实际上,K的每个单形(a0a1…aq)规定K的一个抽象单形(c0c1…cq)。这样规定的K,显然是一个抽象复形,且称K为K的一个几何实现。
2 邻域同调学习算法设G=(V(G), E(G))是一个简单连通图。显然,一个简单连通图就是一个单纯复形,根据上述定义即可以看成是有限个单形的集合,V(G)={a0, a1, …, aα0-1表示图G的α0个顶点的集合也就是图G中所有0维单形的集合,E(G)表示顶点之间的所有连接边的集合。令X和F分别是G的一个顶点子集和边子集,就以G-X表示G去掉X中的点及其关联边而得的图,G-F表示G去掉F中的边而得到的图。设a是G的任意一个顶点,以N(a)表示a的邻域,那么N(X)表示X中所有点邻域的并,即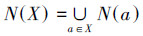
基于此,可以构造出一幅给定图形G的领域复形N(G),N(G)是以G的顶点为顶点,以G中具有公共邻接点的子集为单形的一个抽象复形。根据抽象复形的概念,可以看出任意的抽象复形都可以在欧氏空间实现[25]。因此邻域复形在欧氏空间中是有其相对应的单纯复形的,这里仍以N(G)记邻域复形所对应的单纯复形。除非特殊说明,二者不加以区别,统称为G的邻域复形。下文中的N(G)即指邻域复形在欧氏空间中所对应的单纯复形。
由于构造出的任意图形的邻域复形N(G)可以看成是单纯复形,那么可以将N(G)剖分成有限个单形,根据定义2可表示为N(G)={Aiq; q=0, 1, …, dim(N(G)), i=1, 2, …, αq};对每个单形取定一个指向并记为σiq,根据定义1,每个单形σiq都可以根据顶点坐标线性表示出来;再由式(1)将q维单形线性组合就能得出N(G)的q维链,这些q维链组成的自由交换群即为N(G)的q维链群Cq(N(G))。再通过计算同调群,就可以得出2个图形之间的一种同调关系。设有2个图G、H, 如果N(G)和N(H)的各阶同调群分别同构,就称G和H是邻域同调的,记为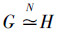
当然,不同类型的连通图,它们是邻域同调的充分必要条件也是不一样的。例如,2个仙人掌图是邻域同调的,当且仅当这2个图都是二分图或都不是二分图且它们的非4-圈[26]的圈数相同[27]; 同样对于两幅立方图(每个顶点的次数都等于3的有限简单连通图)来说,它们是邻域同调的充要条件是两幅图的二分性相同且D值相同[28]; 而两个不含4-圈的图是邻域同调的充要条件则是它们的二分性相同且圈秩相同[29]。
基于上述理论,文中给出了一种邻域同调学习算法(neighborhood homology learning algorithm, NHLA)。该算法主要是针对简单联通图(不含孤立顶点的有限简单图)的分类,通过图形的邻域复形的同构性判断出图形是否是邻域同调,从而进行邻域同调分类。
假设有一个由n幅图组成的样本集G={G1, G2, …, Gn}。根据邻域复形的的概念,为每一个Gi,i∈[1, n]构造出其邻域复形N(Gi),并计算出N(Gi)的q阶同调群,其中0≤q≤dim(N(Gi))。然后判断N(Gi)和N(Gj)的各阶同调群是否同构,进而判断出Gi(i∈[1, n-1])与Gj(j∈[i+1, n])是否邻域同调的。最终根据图之间的邻域同调性,可将图分为k类,则输出集合可表示为H={H1, H2, …, Hk}。具体算法步骤如下:
算法 邻域同调学习算法
输入:待测样本集合G={G1, G2, …, Gn}。
输出:分类后的集合H={H1, H2, …, Hk}。
1)置每个样本Gi为一个类,则G1, G2, …, Gn,共形成n个类;
2)找出Gi的任意一个顶点的邻域,那么Gi中的所有顶点邻域的并集即为所要构造的邻域复形N(Gi);
3)根据式(3)和式(4)计算出每个Gi邻域复形N(Gi)的q维链群Cq(N(Gi)),此时可以得到形如式(5)的一个序列:
 |
4)再由式(6)和式(7)分别可以求出邻域复形N(Gi)的q维闭链群Zq(N(Gi))和q维边缘链群Bq(N(Gi));
5)根据Hq(N(Gi))=Zq(N(Gi))/Bq(N(Gi))计算出N(Gi)的q维同调群;
6)如果Gi,i∈[1, n-1]与Gj,j∈[i+1, n]的各阶同调群分别同构,则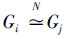
7)通过上述步骤可将样本分成k类,输出H={Hi}i=1k。
由上面的算法可得定理1。
定理1 NHLA算法的所需时间复杂度为Ο(n2),空间复杂度为Ο(n)。
证明 假设有一任意图形G,顶点集为V(G)={a0, a1, …, aα0-1},根据每个顶点的邻域可以构造出它在欧几里德空间里的邻域复形N(G)=Aiq; q=0, 1, …, dim(N(G)), i=1, 2, …, αq}。
根据步骤2),对于n个待测的图形样本,需构造出n个邻域复形,因此本文可以得到2)的时间复杂度为Ο(n),空间复杂度为Ο(n)。
根据步骤3)~5),求出每个邻域复形相对应的q维同调群,此时的时间复杂度为Ο(n),空间复杂度为Ο(n)。
根据步骤6)程序主体,通过for循环进行判断分类直到分类完毕并最终输出分类结果,这里时间复杂度为Ο(n2),空间复杂度为Ο(n)综上可得,NHLA算法的时间复杂度为Ο(n2),空间复杂度为Ο(n)。
3 实验分析为了验证本文算法的有效性,本文进行了3组实验。第1组实验是人工数据,第2组是手写数字识别实验,第3组是实物图像。在实验中,本文方法同时也和SVM、TVQ方法进行了对比。本文实验均在MATLAB平台上实现。
3.1 人工数据本文给出了一次随机生成的二维的连通图集数据,该人工数据是3类服从高斯分布的随机数据,每次生成数据时,每类样本是100个。其中符号‘*’,‘o’和‘▽’分别表示不同的类别,将其可视化如图 1(a)所示。图中的每个点表示每个二维图形所在的位置,是用图形的重心坐标表示的。
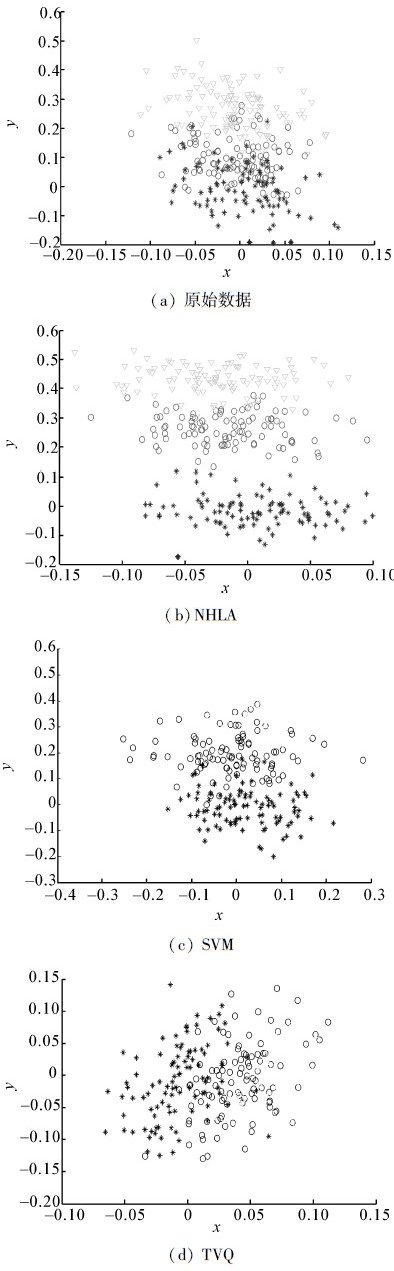
|
| 图 1 随机数据和可视化结果 Fig. 1 Random data and the result of visualization |
分类之前首先对生成图形G进行处理,即需要先提取图形边缘点。将提取的边缘点用V(G)表示,这些边缘点间的连接边用E(G)表示。接着根据邻域复形构造原理构造出N(G),然后再利用上述的邻域同调学习算法进行分类,分类结果如图 1(b)所示。图 1(c)和图 1(d)分别是用SVM和TVQ算法分类后的结果。图 1(a)中随机生成的这几类数据有交叉重叠部分,且从图 1(b)~(d)可以看出,经过NHLA、SVM和TVQ等3种算法分类后,数据都能不同程度的分开。但比较分类后的3幅图可以看出,本文提出的邻域同调学习算法分类后的效果是明显好于另2种算法。
3.2 手写数字识别实验本实验采用USPS_ALL数据库的手写数字集进行实验。此手写数字集包含10个数字(0, 1,…,9)的图片,每个数字含有1 100张字迹不同的图片,每张图片的像素大小为16×16。部分图像如图 2。
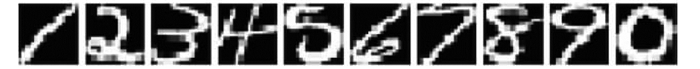
|
| 图 2 USPS_ALL数据库部分图像实例 Fig. 2 Part of the images in USPS_ALL |
实验中,从每类数字中选取一定数量的图像构成样本集。样本集大小从1 500变化到4 500。为消除选择样本的随机独立性,独立重复实验100次,最后取平均识别率作为最终识别率。图 3给出了几种算法在数字手写数据集上不同样本点个数情况下的实验结果。分类前对图像的边缘处理和人工数据实验是相同的。图 3中,随着选取样本个数的增加,各个方法的识别精度也是随之增加的,而且本文提出的邻域同调算法始终是好于SVM和TVQ的。

|
| 图 3 手写数字集上的识别率 Fig. 3 Recognition accuracy on the USPS_ALL database |
采用MPEG7 CE-Shape1 Part B图像库对实物图像进行分类。该图像库是一个图像模版库,包含了各种形状特征的物体模版图,由70类物体、每类20幅共1 400幅实物图像组成。部分图像如图 4。
|
| 图 4 部分实物图像 Fig. 4 Part of the images in MPEG7 CE |
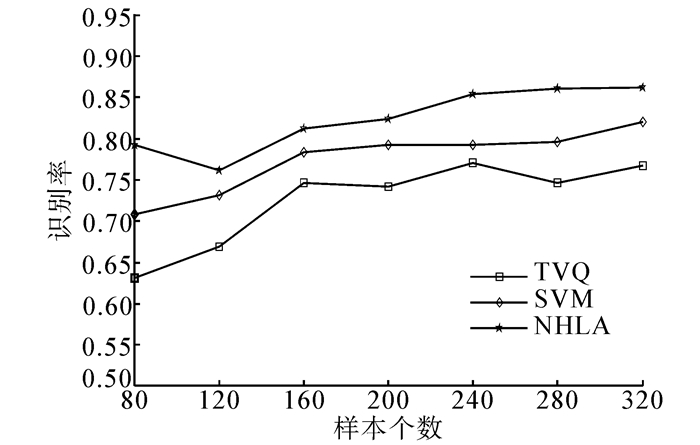
本文在MPEG7 CE-Shape1 Part B图像库中选取其中16类,即共320幅图像进行实验。从每类中选取一定数量的图像构成样本集。其中样本集的大小从80变化到320。为了消除选择样本的随机独立性,独立重复实验100次,最后取平均识别率作为最终识别率。图 5给出了在MPEG7 CE-Shape1 Part B图像库上,几种算法在选取不同样本点个数情况下的实验结果。
|
| 图 5 MPEG7 CE上3种算法的识别率 Fig. 5 Recognition accuracy on the MPEG7 CE database |
从图 5中可以看出,选取的样本个数越多,各个方法的识别精度整体趋势也是随之增加。此外在样本较少的情况下,由于部分图像受到噪声的干扰,本文提出的NHLA算法识别率受到一定的影响,其识别效果不稳定,有一点降低的趋势。但是与其他算法相比较,NHLA依然具有较好的识别精度。而且随着样本的增多,识别率受噪声干扰的程度也减小,仍是处于增长趋势的。
4 结束语针对边缘可变的划分问题,本文提出了邻域同调学习算法,该算法引进了同调理论,利用复形之间的性质,通过构造图形的邻域复形,并判断这些邻域复形是否同构来进行对图集的邻域同调分类。利用该算法进行分类能够有效地保证在分类过程保持图形原有的结构特征不变。
通过实验对比可以看出,本文提出的算法的识别率较高,具有一定的优势。但是,本文的算法目前只实验于二维图像上,对于更高维的图像分类还有待完善,另外本算法对噪声和扰动的鲁棒性也有待提高。总之,邻域同调学习算法具有比较坚实的理论基础,是一种可持续发展的学习方法。
| [1] | 周志华, 王珏. 机器学习及其应用研究[M]. 北京: 清华大学出版社, 2007 : 1 -161. |
| [2] | 李凡长, 张莉, 杨季文. 李群机器学习[M]. 合肥: 中国科学技术大学出版社, 2013 : 281 -296. |
| [3] | PERNKOPF F, WOHLMAYR M, TSCHIATSCHEK S. Maximum margin Bayesian network classifiers[J]. Pattern Analysis and Machine Intelligence , 2012, 34 (3) : 521-532 DOI:10.1109/TPAMI.2011.149 |
| [4] | PANWAR H, GUPTA S. Advances in Computer Science, Engineering and Applications[M]. Berlin: Springer, 2012 : 385 -392. |
| [5] | EIDELMAN V. Optimization strategies for online large-margin learning in machine translation[C]//Proceedings of the 7th Workshop on Statistical Machine Translation, Montreal, Canada, 2012: 480-489. |
| [6] | VAPNIK V. Statistical learning theory[M]. New York: Wiley, 1998 : 1 -768. |
| [7] | LEE Y J, HSIEH W F, HUANG C F. e-SSVR:A smooth support vector machine for e-insensitive regression[J]. IEEE Transactions on Knowledge and data Engineering , 2005, 17 (5) : 678-685 DOI:10.1109/TKDE.2005.77 |
| [8] | LIN C F, WANG S D. Fuzzy support vector machines[J]. IEEE Transactions on Neural Networks , 2002, 13 (3) : 466-471 |
| [9] | FABIO A, ALESSANDRO S. A re-weighting strategy for improving margins[J]. Artificial Intelligence , 2002, 137 : 197-216 DOI:10.1016/S0004-3702(02)00122-4 |
| [10] | 鲜敏, 李凡长. 一种同调边缘学习算法[J]. 计算机工程与应用 , 2008, 44 (21) : 192-194 XIAN Min, LI Fanzhang. Learning algorithm based on homology margin[J]. Computer Engineering and Applications , 2008, 44 (21) : 192-194 |
| [11] | 杨季文, 李哲硕, 何书萍, 等. 胞腔同调边缘学习算法研究[J]. 计算机研究与发展 , 2013, 50 (5) : 1005-1011 YANG Jiwen, LI Zheshuo, HE Shuping, et al. On celluar homology margin learning algorithms[J]. Computer Research and Development , 2013, 50 (5) : 1005-1011 |
| [12] | 邓乃杨, 田英杰. 数据挖掘中的新方法——支持向量机[M]. 北京: 科学出版社, 2005 : 1 -408. |
| [13] | BURGES C J C. A tutorial on support vector machines for pattern recognition[J]. Data Mining and Knowledge Discovery , 1998, 2 (2) : 121-167 DOI:10.1023/A:1009715923555 |
| [14] | SHAWE-TAYLOR J, CRISTININI N. Kernel methods for pattern analysis[M]. Cambridge University Press, 2004 : 289 -436. |
| [15] | CORTES C, VAPNIK V. Support-vector networks[J]. Machine Learning , 1995, 20 (3) : 273-297 |
| [16] | SIMARD P Y, LECUN Y, DENKER J. Efficient pattern recognition using a new transformation distance[J]. Advanced in Neural Information Processing System , 1993, 5 : 50-58 |
| [17] | SCHAPIRE R E, SINGER Y. Improved boosting algorithms using confidence-rated predictions[J]. Machine Learning , 1999, 37 (3) : 297-336 DOI:10.1023/A:1007614523901 |
| [18] | DUFFY N, HELMBOLD D. Boosting methods for regression[J]. Machine Learning , 2002, 47 (2/3) : 153-200 DOI:10.1023/A:1013685603443 |
| [19] | 南基洙, 王颖. 同调代数导论[M]. 大连: 大连理工大学出版社, 2011 : 112 -222. |
| [20] | 姜伯驹. 同调论[M]. 北京: 北京大学出版社, 2006 : 1 -90. |
| [21] | 江泽涵. 拓扑学引论[M]. 上海: 上海科学技术出版社, 1978 : 25 -169. |
| [22] | 孟道骥, 白承铭. 李群[M]. 北京: 科学出版社, 2003 : 28 -92. |
| [23] | 黄保军. 同调与同伦原理[M]. 合肥: 中国科学技术出版社, 2005 : 16 -59. |
| [24] | 沈信耀. 同调论——代数拓扑学之一[M]. 北京: 科学出版社, 2002 : 19 -132. |
| [25] | 谢力同. 组合拓扑方法在图论和拟阵理论中的应用[J]. 数学进展 , 1983, 12 (3) : 1-5 XIE Litong. Applications of combinatorial topology method in graph theory and matroid theory[J]. Advances in Mathematics , 1983, 12 (3) : 1-5 |
| [26] | 方冬云. 不包含{4, 8, 9}-圈平面图结构的性质[J]. 长春工业大学学报 , 2011, 32 (5) : 485-488 FANG Dongyun. Nature of stucture planar graph without {4, 8, 9}-cycles[J]. Journal of Changchun University of Technology , 2011, 32 (5) : 485-488 |
| [27] | 薛秀谦. 仙人掌图的邻域同调分类[J]. 山东大学学报 , 1994, 29 (1) : 13-17 XUE Xiuqian. The neighborhood homology classification of cactus[J]. Journal of Shandong University , 1994, 29 (1) : 13-17 |
| [28] | 薛秀谦. 立方图的邻域同调分类[J]. 中国矿业大学学报 , 1995, 24 (4) : 110-112 XUE Xiuqian. The neighborhood homology classification of cubic graphs[J]. Journal of China University of Mining and Technology , 1995, 24 (4) : 110-112 |
| [29] | 薛秀谦. 无C4图的邻域同调分类[J]. 系统科学与数学 , 1998, 18 (1) : 101-103 XUE Xiuqian. The neighborhood homology classification of the C4 free graphs[J]. Systems Science and Mathematics , 1998, 18 (1) : 101-103 |



