2. 天津市智能机器人技术重点实验室,天津 300071
2. Key Laboratory of Intelligent Robotics of Tianjin, Tianjin 300071, China
近年来,多智能体系统受到了越来越多的关注。所谓多智能体系统是指由多个可自主计算的智能体组成的系统,它具有自组织、学习和推理等能力以及自主性、分布性和协调性等特点,在系统中每个智能体仅需与邻居进行信息交互,便能完成一个整体的期望目标。多智能体技术有着广泛的应用背景,譬如可用于编队控制、交通流控制、分布式信息融合以及生物、经济、工程等领域[1-4]。
随着无线通信技术以及计算机技术的快速发展,使多个智能体组成的群体系统通过协调、合作来完成原本由单个智能体无法或难以完成的工作已经成为可能。多智能体系统具有单个智能体难以拥有的丰富的感知能力、高效率的并行执行能力、优秀稳定的鲁棒性和卓越的容错能力等优势,因此使得智能体在实际工作环境中的可适应性及实用性均得到了大幅提高。而多智能体编队问题是对于多智能体协调合作问题所开展的研究中的一个典型应用。多智能体编队控制主要是指多个智能体在群体运动过程中,能够在克服环境限制的同时还保持着期望队形,最终都能够顺利到达指定目的地的控制技术。多智能体的编队控制是目前对多智能体协调合作问题进行研究的重要基础,引起了国内外广大学者的关注,是国内外进行多智能体系统研究的热点课题。目前,常用的多智能体编队控制方法主要有分布式控制、基于行为法、虚结构法、人工势场法和领航跟随法等[5]。
在以上几种编队方法中,领航—跟随法得到了广泛应用,并且成为最普遍采用的编队方法之一[6]。领航跟随法的基本思想是在多个智能体组成的群体中,某个智能体被指定为领航者,其余作为它的跟随者,跟随者以一定的距离间隔跟踪领航智能体的位置和方向[7]。对于领航—跟随法有2种控制器形式[5, 8]:控制器和l-φ控制器。l-φ控制器的控制目标是使跟随者和领航者之间的距离和相对转角达到设定值[9]。l-l控制器考虑的是3个机器人之间的相对位置问题,当跟随者和2个领航者之间的距离达到设定值时,就可以认为整个队形稳定了。
文中通过引入基于邻居的局部控制律以及基于邻居的状态估计规则[9-13]设计了一种领航跟随编队算法的新型控制器,在控制器中通过简单地设定跟随者和领航者之间的相对坐标即可轻松实现任意形状编队,并为了将所有跟随者相对于领航者的相对坐标统一映射到领航者的坐标系中,在控制器中引入了“坐标旋转公式”[14],用于实现整个队形的对称轴和领航者的运动方向平行,即所编队形随着领航者的运动方向的改变做相应旋转。文中设计的这种新型控制器,既突破了l-l控制器中机器人个数的限制又避免了l-φ控制器设计偏复杂的缺点。文中分别给出了固定拓扑和切换拓扑下的系统稳定编队的充分条件及相应的证明。文章的最后分别通过MATLAB仿真和在Amigobot机器人平台上做实验来验证该算法的正确性及实际可行性。
1 相关的图论基础为了讨论方便,简单介绍一些文中能够用到的图论中的一些基本的概念和相关的标记符号。更多图论细节可参阅文献[15]。
图论在连通系统中是非常重要且有效的数学分析工具。一个无向图G=(V, E)是由非空有限顶点集合和无序的元素偶对ek的集合组成,其中ek=(vi, vj)∈E称为图的边。文中假设不存在从一个顶点到它自身的边(vi, vi),而且由于图G是无向图,所以有∀(vi, vj)∈E,(vj, vi)∈E。如果(vi, vj)∈E,那么可以说vj是vi的邻居顶点,则顶点vi的邻居顶点集合定义为Ni={j:(vi, vj)∈E, ∀j≠i}。图中顶点vi到顶点vj的一条路径是指从起始顶点vi到终止顶点vj过程中一系列顶点对组成的连续的边。如果无向图中任何2个顶点至少有一条路径,那么就说这个图是连通的,否则就是非连通的。
在无向图中,用A=(aij)n×n来表示系统的权重邻接矩阵,其中aij满足aii=0且aij=aji≥0。在无向图G中, 节点vi的度定义为di=Σaij,其中j∈N。则图G的度矩阵为对角阵D=diag(d1, d2, …, dn)。那么图G的拉普拉斯(Laplacian)矩阵L=D-A, 显然L是对称矩阵。从L的定义中,可以知道L的每一行元素之和为零,即L·1n=0, 这里1n=(1, 1, …, 1)n×1,从而可以很容易得到L的其中一个特征值为零,其对应的特征向量为1n。
2 控制算法设计在介绍算法设计之前,这里先对系统的连接拓扑图G做一个简要的说明。文中图G的邻接矩阵包括两部分,一部分是所有跟随者之间组成的连通图G的邻接矩阵用表示,相应图G的度矩阵用D表示,而领航者和每个跟随者之间的连接矩阵用B表示。假设系统中包括领航者共有n+1个智能体,那么A为n×n的对称矩阵;B为n×n的对角矩阵,对角线上的元素为跟随者和领航者之间的连接权重值,文中假定图G总是连通的,则B对角线上的元素的值至少有一个不为零,即至少有一个跟随者和领航者是直接连通的,但这种连通是单向的,就是说领航者的运动不受跟随者的影响。当系统的拓扑图在一定时刻变化时,则图G被认为是这n+1个智能体组成的所有可能的拓扑图集合S={G1, G2, …, GM}中的一个,定义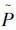
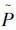
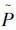
在文中的Leader-Follower多智能体系统中,领航者的运动不受跟随者的影响,并且假定领航者的速度无法被跟随者实时获取。这里首先介绍一下领航者的运动控制律:
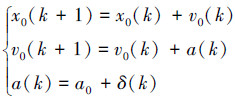 |
式中:x0(k)∈Rm是领航者的位置;v0(k)∈Rm是领航者的速度;a(k)∈Rm是加速度控制输入,a0∈Rm是初始加速度值,为已知的;δ(k)∈Rm为环境噪声扰动是未知的,但是它有一个给定的上限值δ,即‖δ(k)‖≤δ,‖δ(k)‖表示δ(k)的2范数。文中出现的形如‖·‖的表达式均表示2范数,这里m的值可以取任意自然数,但一般取值2和3,因为取值为2和3时分别表示2维平面和三维空间,文中所有的上下标的m取值均为2。
跟随者的运动控制律如式(1)所示:
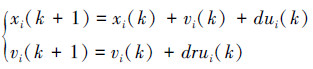 |
(1) |
式中:xi(k)∈Rm是第i个跟随者的位置;vi(k)∈Rm是第i个跟随者的速度;d和r均为控制常量参数,在后面将给出它们的取值范围。
由于领航者和其他邻居跟随者的速度无法实时获取,又因为他们的位置信息可以实时得到,故式(1)中的ui(k)∈Rm为第i个跟随者的基于邻居位置信息的控制器输入,其表达式为
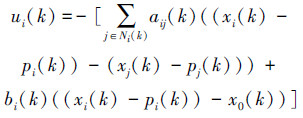 |
(2) |
式中:
 |
 |
i, j=1, 2, …, n,αij>0,βi>0。
这里首先对坐标系问题做一个简要说明:文中假定有2个坐标系,一个是绝对坐标系,另一个是领航者坐标系,但无论是领航者还是跟随者,它们的实际坐标均是基于绝对坐标系的。这里的领航者坐标系定义为:以领航者的绝对坐标作为它自身坐标系的坐标原点,并以它的运动方向作为它自身坐标系的x轴正方向。所以领航者自身的坐标系其实是以领航者的角速度大小(顺时针时其大小为负值)相对于绝对坐标系做顺或逆时针方向的旋转,加上领航者同时以一定的线速度在运动,故领航者坐标系相对于绝对坐标系一边做旋转运动一边沿着领航者的运动轨迹做平移运动。譬如当领航者做逆时针方向的匀速圆周运动时,领航者坐标系相对于绝对坐标系则是一边以恒定的角速度做逆时针方向的旋转运动一边以恒定的线速度沿着领航者的圆周运动轨迹做平移运动。
式(2)中的pi(k)=Ri(k)Ci∈Rm为实现编队的控制参数。其中Ci=[px i pyi]T为绝对坐标系下系统稳定时第i个跟随者相对于领航者的相对坐标位置。为描述方便,这里以3个智能体甲为领航者、乙丙均为跟随者编队成为等腰三角形为例进行说明,首先假定“前方”指X轴正方向,“上方”指Y轴正方向,那么假定甲在前方,乙和丙在甲的后方且乙在丙的上方,同时乙丙连线是等腰三角形底边,设定甲乙丙到底边中点的距离都为M,如图 1(a)所示,则如果此时甲的坐标为(x, y),乙丙的坐标分别为(x1, y1)、(x2, y2),那么有
 |
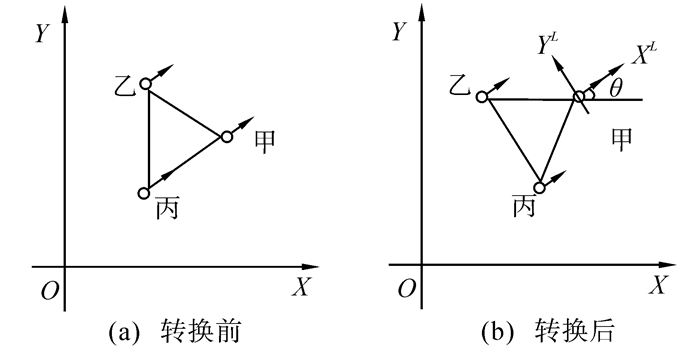
|
| 图 1 相对坐标转换对比图 Fig. 1 The comparison of Relative coordinate transformation |
故当队形一定时pxi和pyi为定值。为描述简便,这里不妨假设系统稳定时领航者在绝对坐标系中的坐标始终为(0, 0),那么Ci则可看成第i个跟随者在绝对坐标系的坐标,做这样的假设后可以随意设定跟随者坐标以实现任意形状编队。Ri(k)表达式为
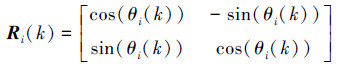 |
它为第i个跟随者第k时刻的坐标旋转矩阵,它能将第i个跟随者在绝对坐标系中相对于领航者的相对坐标转换成在领航者坐标系中相对于领航者的坐标,以实现系统稳定编队时整个队形能够在沿着领航者运动轨迹做平移运动的同时,又能以领航者的角速度大小相对于绝对坐标系做顺或逆时针方向的旋转,如图 1为转换前后示意图。其中的θi(k)为第i个跟随者第k时刻的运动方向与绝对坐标系中X轴正方向之间的夹角,当系统稳定编队时可近似为领航者的运动方向和绝对坐标系中X轴正方向之间的夹角如图 1(b)中的θ,范围为(-π, π)。
2.2 主要结论这里将给出文中的一些主要结论,同时对式(1)中的控制参数d和r的范围做一个界定。
为了方便后期的公式推导,这里首先将式(1)矩阵化处理。定义:
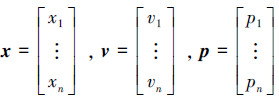 |
则由式(1)和(2)化简可得
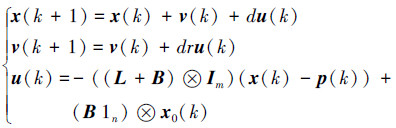 |
(3) |
式中:Im为m×m的单位对角矩阵,1n为n维全1列向量, 即1n=[1 1 … 1]T。
定义跟随者和领航者之间的位置差x(k)和速度差v(k)如下:
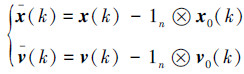 |
(4) |
则由式(3)和(4)化简得
 |
(5) |
式中:In为n×n的单位对角矩阵,H=L+B。
令差值变量为
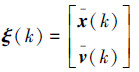 |
则可将式(5)化简为
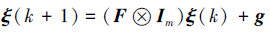 |
(6) |
式中:
 |
(7) |
在给出重要结论之前,这里先给出几个引理。
引理1 如果图G是连通的,那么对称矩阵H是正定的[11]。
引理2(Routh-Hurwitz theorem) 假设一个形如a0xn+a1xn-1+…+an-1x+an=0的n阶多项式,这里a0>0,
 |
则如果i>n, ai=0,当且仅当a1>0, Δ2>0, …, Δn-1>0, an>0时多项式的所有根有负实部。
引理2说明了判定一个给定的系统是否是Hurwitz稳定的,就要看这个系统所对应的特征多项式所有的根是否都存在负实部[16]。
引理3(Schur complement)[17] 对于一个形如下式的对称矩阵S,
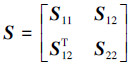 |
这里S11和S22是方阵,那么下列条件等价:
1) S < 0
2) S11 < 0, S22-S12TS11-1S12 < 0
3) S22 < 0, S11-S12S22-1S12T < 0
接下来介绍一下文中的2个重要的定理结论。定理1是关于固定拓扑情况下系统能够达到稳定编队的充分条件,而定理2是关于切换拓扑情况下系统能够达到稳定编队的充分条件。
定理1 已知连接拓扑图G是固定的,并且在任意时刻k都是连通的,此时L和B都是恒定矩阵。则使得系统(3)稳定编队的充分条件是:对任何给定的0 < r < 1,d取值满足0 < d < 4/((2-r)λmax),并且存在一个常量C,使得
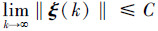 |
式中:λmax表示H的最大特征值。常数C由3组常量δ, pxi, pyi共同决定, i=1, 2, …, n,特别地,当δ=0, pxi=0, pyi=0时,有
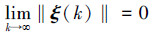 |
式中:δ表征领航者受到环境扰动的。
证明 由已知条件可知,由于图G是固定拓扑且在任意时刻k是连通的,则根据引理1可知,对称矩阵H是正定的。
令U为矩阵H的Schur转换矩阵(酉矩阵),则
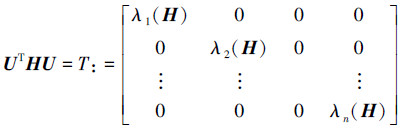 |
这里λi(H)表示矩阵H的第i个特征值,由于矩阵H是正定的,所以λi(H)>0。
令: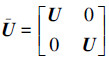

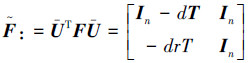
计算|sI2n-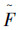
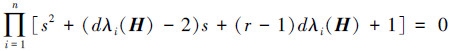 |
(8) |
对式(8)应用双线性变换s=(t+1)/(t-1),整理可以得到式(9):
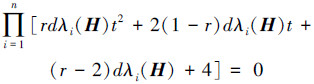 |
(9) |
上面的双线性变换是把S平面上单位圆内部区域映射到复平面t的左半区域。只有当式(9)的所有根都有负实部时,矩阵F才是Schur稳定的。
由于λi(H)>0,结合式(9),通过引理2可知,欲使F是Schur稳定的,可得当且仅当正的常量r和d满足(1-r)d>0、(r-2)dλi(H)+4>0,即0 < r < 1, 0 < d < 4/((2-r)λmax)时才能达到要求,这里的λmax表示H的特征值λi(H)中的最大值,i=1, 2, …, n。
所以当0 < r < 1、0 < d < 4/((2-r)λmax)时,F是Schur稳定的,相应的F 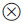
又由于在队形固定的情况下,pxi和pyi是固定的,则二者可以看成是常量,所以易知式(7)中的参数除δ(k)外均为常量,由于‖δ(k)‖≤δ,所以在给定常量r、d、a0(k)、δ、pxi和pyi情况下‖g‖≤C0,这里的C0是基于上述这些常量值的大小而定的有界值。所以‖g‖是有界的,因此在给定条件下存在一个常量C使得:
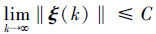 |
定理1证毕。
从定理1的证明过程可以看出,系统稳定编队的充分条件中的r的取值范围在连接拓扑图不变的情况下是固定的,且此时d的取值范围随r取值的增大而增大。接下来的定理2是切换连接拓扑图情况下,系统达到稳定编队时的充分条件,即此时r和d需满足的取值范围。
定理2 已知切换连接拓扑图G在任意时刻k都是连通的,此时L和B均随Ω的变化做相应的改变即它们都是可变矩阵,但在2次相邻拓扑切换时刻点之间是恒定的。则使得系统(3)稳定编队的充分条件是:对任何给定的0 < r < 2λmin/(λmin+λmax),d取值满足:
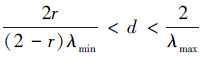 |
(10) |
并且存在一个常量C,使得:
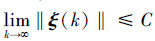 |
式中:λmin为H的最小特征值,λmax表示H的最大特征值。常数C由3组常量δ、pxi、pyi共同决定,i=1, 2, …, n。特别地,当δ=0, pxi=0, pyi=0时,有
 |
式中:δ表征领航者受到环境扰动。
证明 构造一个李雅普诺夫函数
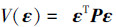 |
其中对称矩阵P为
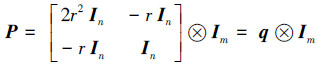 |
则V(ε)的差分为
 |
化简FTqF-q得
 |
令
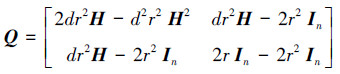 |
则有
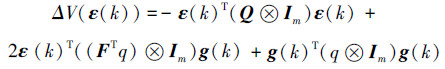 |
由引理3以及式(10)可知,Q是正定矩阵。
注意到对于V(ε)有:
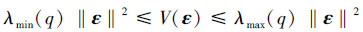 |
(11) |
由式(11)可得
 |
式中: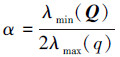
 |
因为式(7)中的r、d、a0(k)、δ、p(k)均为已知量,又由于‖H‖的值是有界的,不妨设其最大边界值为Hmax,则可知‖g‖≤C0,这里常量C0的大小决定于r、d、a0(k)、δ、p(k)以及Hmax的值。
结合式(11)可得
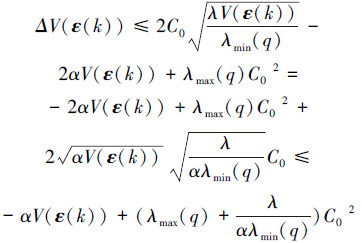 |
这里λ表示(FTq)TFTq的最大特征值。进而可得
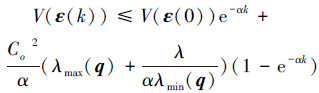 |
则有
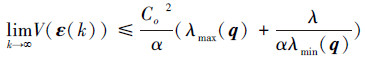 |
(12) |
由式(11)和式(12),可以得到C的一个限定值为
 |
因此有
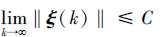 |
即在切换拓扑下系统能够达到稳定并实现一致性编队。定理2证毕。
从定理1和定理2可知,文中的基于领航跟随法的编队控制器设计的核心是设定控制参数r和d的取值范围。二者可以看作系统收敛过程中的波动强度因子,顾名思义当它们的值在给定范围内比较大时系统在收敛的过程中波动比较大也就使得超调量较大,从而使系统可能需要经过很长时间才达到稳定或者一直处于调节状态,并且在这种情况下如果用实际机器人做实验,由于速度剧烈波动可能对机器人的机械结构有损害。而当它们取值都比较小时,虽然在系统收敛的过程中波动较小,但是可能达到稳定的调节时间会更长。所以只有当二者在给定范围内经过多次仿真实验或者凭经验取到合适值时才能使系统收敛并很快稳定从而实现预期编队。
3 实验结果本节将分别采用MATLAB软件仿真和在美国MobileRobots公司生产的Amigobot实验平台上做实验来验证算法的正确性和实际可行性。该实验部分主要采用将3个智能体的MATLAB仿真效果和在3个Amigobot机器人上做实验的效果做对比的形式进行展开。3个智能体中一个做领航者,另外两个做跟随者,目标设定编成等腰三角形的队形。为了体现文中提出的算法能够比较方便地编出任意队形特意用MATLAB做了几个其他复杂队形的仿真。Matlab仿真及实际机器人的实验所需要的通信拓扑以如下一种固定拓扑为例进行:
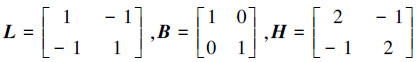 |
这里取r=0.1,通过简单计算可得这4种拓扑图中4/((2-r)λmax)=0.7018,不妨取d=0.1,所有智能体的初始坐标和方向以及初始速度的大小均可随机产生,为了方便,文中设定它们的初始方向均指向x轴正方向,且其中领航者甲的坐标为(0, -2),跟随者乙的坐标为(0, 0),丙的坐标为(0, -1),领航者的速度大小取‖v0‖=0.1(m.s-1),乙和丙初速度大小为0。且乙和丙相对于甲的相对坐标分别设为(px1, py1)=(-1, 1), (px2, py2)=(-1, -1)。
3.1 MATLAB仿真结果仿真结果如图 2所示。
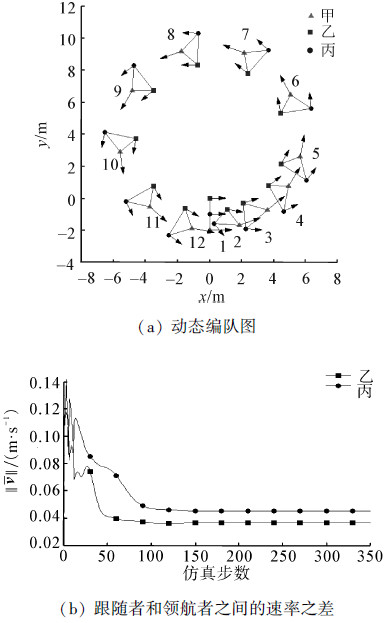
|
| 图 2 Matlab仿真结果 Fig. 2 The results of Matlab simulation |
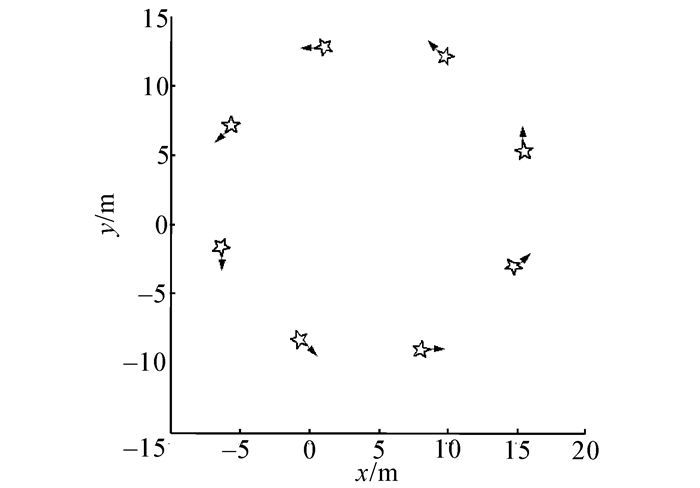
图 2(a)中动态编队部分选取了12个时刻的队形并按时间顺序做了相应的编号,其中横纵坐标指长度分别用x和y表示,单位为m,小三角形表示领航者甲,其上的最长的箭头表示甲的方向,图中小正方形表示跟随者乙,小圆点则表示跟随者丙,其上2个稍短的箭头则分别表示它们各自的方向,图 2(b)中由小正方形和黑色小圆点标识的两条曲线分别表示图 2(a)中对应的乙和丙2个跟随者与领航者之间的线速度之差,横坐标表示仿真步数,单位为1,纵坐标用v的范数‖v‖表示,单位为m.s-1。图 2(a)中编号为1的队形是初始时刻的队形为一条直线,后面经过依次调整最终接近于期望的稳定的等腰三角形队形。从图(b)可以看出,当系统经过150步左右后达到稳定。由于领航者在做圆周运动,丙在外圈,乙在最内圈,故从图中数据可知跟随者和领航者之间的线速度之差的绝对值曲线属于正常现象,如果领航者做直线运动线速度之差基本相同且接近于0。为了体现文中提出的算法能够比较方便地编出任意队形,这里特意做了几个相关仿真。如图 3~5所示,分别用7、9、10个智能体编出了箭头、斧子和五角星3种形状的队形,为简便起见,图中只用黑色箭头标示出领航者的运动方向。
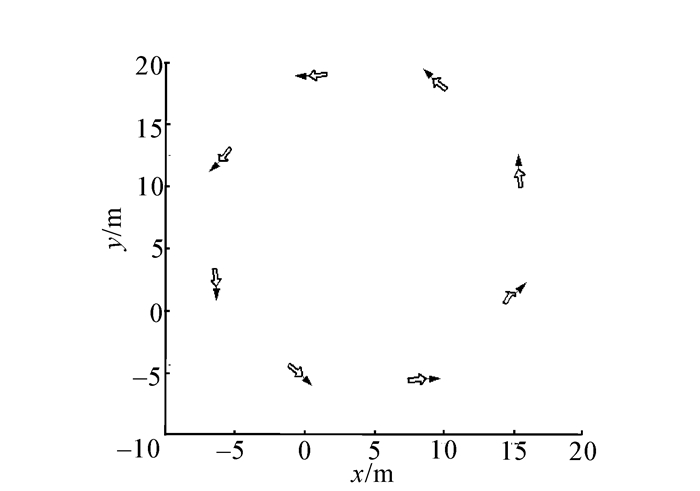
|
| 图 3 箭头队形 Fig. 3 The arrow formation |
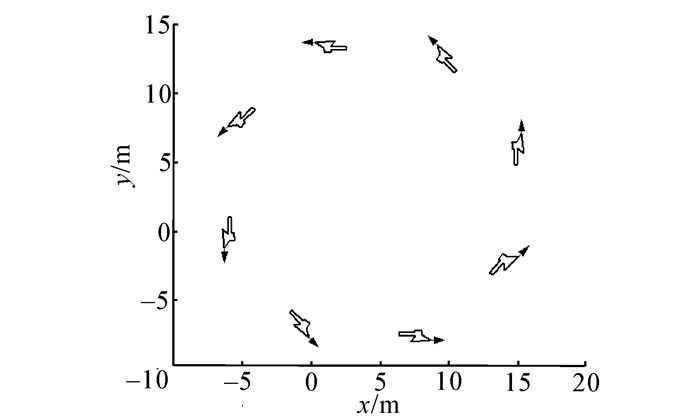
|
| 图 4 斧子队形 Fig. 4 The axe formation |
|
| 图 5 五角星队形 Fig. 5 The pentagram formation |
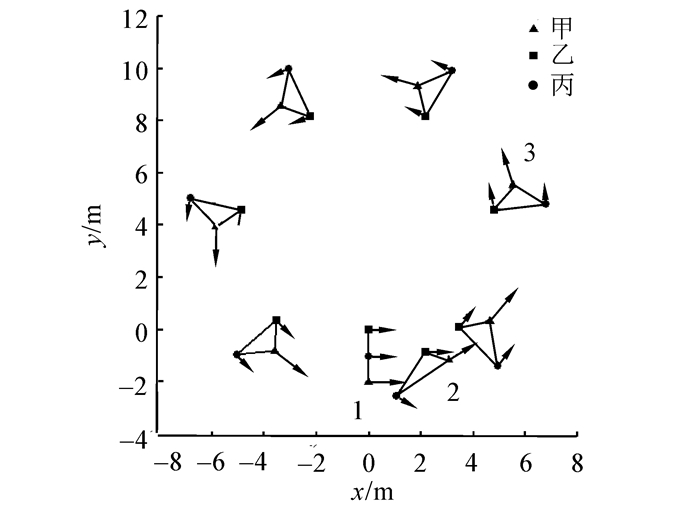
图 6为在Amigobot机器人上做实验,然后将实验过程中的机器人的位置坐标以及运动速度大小和方向打印到本地txt文档中,然后通过MATLAB读取相应文档的数据画出实验效果图,画该效果图时文中选取了实验开始时的几个相隔相对比较密集的3组数据加上中间分布均匀的一些数据。
|
| 图 6 Amigobot机器人实验结果 Fig. 6 The experimental result of Amigobot robots |
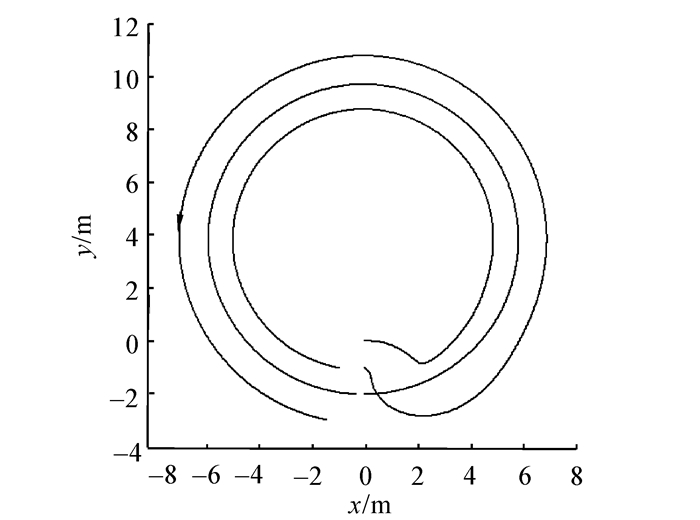
从图 6可知,3个机器人能快速成功地实现编队,然后稳定地按预期的队形运动,从而进一步验证了文中算法的正确性以及实际可行性。图 7所示是整个实验过程中Amigobot机器人的运动轨迹图。从图 2中的(a)和图 6可以看出系统都能够快速收敛,实现预期的稳定编队控制效果,进而从2个方面验证了文中所提出的算法的正确性。图 8中的(a)~(c)分别对应图 6中的编号为时刻1~3的实验图。从图 8的实验图可以更加直观地看出文中所设计的新型领航跟随控制器的编队算法的实际可行性。
|
| 图 7 机器人运动轨迹图 Fig. 7 The motion track of robots |

|
| 图 8 多机器人编队的实验图 Fig. 8 The experiment of multi-robot formation |
文中假定在该多智能体系统中,每个智能体的速度无法被他们的邻居智能体实时获取,但位置坐标信息是可以被它的邻居获得的,在这种情况下,采用邻居的局部控制律以及邻居的状态估计规则的思想来设计控制器输入。在算法中,通过设定跟随者和领航者之间的相对坐标,在智能体个数满足的情况下能够很方便地实现任意形状编队。为了将所有跟随者在绝对坐标系中相对于领航者的相对坐标转换成在领航者坐标系中相对于领航者的坐标,引进坐标旋转公式实现了整个队形能够随着领航者的运动方向的变化做相应旋转,该公式的引入在一定程度上也让领航者表现出了明显的主导性。文中还分别给出了固定拓扑和切换拓扑时的重要定理结论,且分别通过理论详细地证明了算法的正确性。
| [1] | VICSEK T, CZIRÓK A, BEN-JACOB E, et al. Novel type of phase transition in a system of self-driven particles[J]. Physical Review Letters , 1995, 75 (6) : 1226-1229 DOI:10.1103/PhysRevLett.75.1226 |
| [2] | JADBABAIE A, LIN J, MORSE A S. Coordination of groups of mobile autonomous agents using nearest neighbor rules[J]. IEEE Transactions on Automatic Control , 2003, 48 (6) : 988-1001 DOI:10.1109/TAC.2003.812781 |
| [3] | 刘佳, 陈增强, 刘忠信. 多智能体系统及其协同控制研究进展[J]. 智能系统学报 , 2010, 5 (1) : 1-9 LIU Jia, CHEN Zengqiang, LIU Zhongxin. Advances in multi-Agent systems and cooperative control[J]. CAAI Transactions on Intelligent Systems , 2010, 5 (1) : 1-9 |
| [4] | PENG Z, WEN G, RAHMANI A, et al. Leader-follower formation control of nonholonomic mobile robots based on a bioinspired neurodynamic based approach[J]. Robotics and Autonomous Systems , 2013, 61 (9) : 988-996 DOI:10.1016/j.robot.2013.05.004 |
| [5] | 杨甜甜, 刘志远, 陈虹, 等. 移动机器人编队控制的现状与问题[J]. 智能系统学报 , 2007, 2 (4) : 21-25 YANG Tiantian, LIU Zhiyuan, CHEN Hong, et al. Formation control of mobile robots: state and open problems[J]. CAAI Transactions on Intelligent Systems , 2007, 2 (4) : 21-25 |
| [6] | PENG Z, WEN G, RAHMANI A. Leader-follower formation control of multiple nonholonomic robots based on backstepping[C]//Proceedings of the 28th Annual ACM Symposium on Applied Computing. Coimbra, Portugal, 2013: 211-216. |
| [7] | 苏治宝, 陆际联. 多移动机器人队形控制的研究方法[J]. 机器人 , 2003, 25 (1) : 88-91 SU Zhibao, LU Jilian. Research approach to formation control of multiple mobile robots[J]. Robot , 2003, 25 (1) : 88-91 |
| [8] | CHOI I S, CHOI J S, CHUNG W J. Leader-follower formation control without information of heading angle[C]//IEEE/SICE International Symposium on System Integration (SII). Fukuoka, Japan, 2012: 842-846. |
| [9] | CHEN X, SERRANI A, OZBAY H. Control of leader-follower formations of terrestrial UAVs[C]//Proceedings of 42nd IEEE Conference on Decision and Control. Maui, USA, 2003, 1: 498-503. |
| [10] | LIU Z X, CHEN Z Q. Discarded consensus of network of agents with state constraint[J]. IEEE Transactions on Automatic Control , 2012, 57 (11) : 2869-2874 DOI:10.1109/TAC.2012.2190199 |
| [11] | HONG Y G, HU J P, GAO L X. Tracking control for multi-agent consensus with an active leader and variable topology[J]. Automatica , 2006, 42 (7) : 1177-1182 DOI:10.1016/j.automatica.2006.02.013 |
| [12] | CHEN Z Q, XIANG L Y, LIU Z X, et al. A tracking control scheme for leader based multi-agent consensus for discrete-time case[C]//27th Chinese Control Conference. Kunming, China, 2008: 494-498. |
| [13] | WANG F, GAO L, WANG L. Tracking control for multi-agent consensus for discrete-time case[C]//Control and Decision Conference(CCDC). Mianyang, China, 2011: 923-928. |
| [14] | 张伟, 张安堂, 肖宇. 基于坐标旋转数字计算方法的三维坐标变换[J]. 探测与控制学报 , 2011, 33 (2) : 73-76 ZHANG Wei, ZHANG Antang, XIAO Yu. Cordic based three-dimensional coordinate transform[J]. Journal of Detection & Control , 2011, 33 (2) : 73-76 |
| [15] | GODSIL C D, ROYLE G, GODSIL C D. Algebraic graph theory[M]. New York: Springer, 2001 : 1 -420. |
| [16] | MERRIS R. Laplacian matrices of graphs: a survey[J]. Linear algebra and its applications , 1994, 197 : 143-176 |
| [17] | HORN R A, JOHNSON C R. Matrix analysis[M]. Cambridge: Cambridge University Press, 2012 : 1 -541. |



