多标记数据[1]中每个样本可以同时带有多个类标,并且广泛地出现在不同的应用领域,比如文本分类、媒体标注、信息检索、生物信息学等。对于这种数据的分析需要利用多标记学习技术[2-3]。由于大量不同的多标记学习技术被提出,所以该技术仍是研究热点,目前可以分为问题转化和算法适应2种类型。在问题转化类型中,BR(binary relevance), CC(classifier chain)和RAkEL(random k-labelsets)分类器是典型代表。而在算法适应类型中,MLkNN(multi-label k nearest neighbor)、AdaBoost.MH(adaboost multi-class hamming trees)和RankSVM(rank support vector machine)属于将一些先进的单标记分类器转化为多标记分类器的一类。LEAD(multi-label learning by exploiting label dependency)和LIFT(multi-label learning with label-specific features)分类器则更进一步,考虑到特征子集和利用类标的层级结构去进行学习分类的一类。多标记学习技术发展的动力来自于实际应用问题,很具有研究价值。
虽然多标记学习技术还需要许多研究工作,但是很少的科研工作者将目光转向数据集中一些不相关或冗余的特征。减少这些特征会在一定程度上提高多标记学习器的分类能力,因此对数据集进行特征选择预处理是很有必要的。特征选择[4-5]的目的是在高维数据中降低子集维度,主要有过滤式、包装式和嵌入式等3种不同形式。过滤式与目标学习器无关,具有计算简单,效率高的优势[6-7]。本文提出一种过滤式多标记特征选择的框架,并以卡方检验[8]为特征评价的准则。
1 过滤式多标记特征选择框架过滤式方法的基本思想是使用一种独立于分类器的评价指标来衡量某个特征的好坏,即选择该特征优先级。过滤式方法在计算效率上往往优于其他2种特征选择方法。
卡方检验可以用来度量特征t和类标c之间的相关程度。假设t和c之间符合具有一阶自由度的CHI分布。t和c的CHI值由式(1)计算:
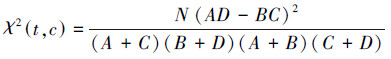 |
(1) |
式中:χ2值表示CHI值,N表示数据集中样本的总个数;A表示包含t且属于分类c的样本数;B为包含t但是不属于c类的样本数;C表示属于c类但是不包含t的样本数;D表示既不属于c也不包含t的样本数。可以看出N固定不变,A+C为属于c类的样本数,B+D为不属于c类的样本数,所以式(1)可以简化为
 |
当特征和类标相互独立时,χ2(t, c)=0。χ2(t, c)的值越大,特征t和类标c越相关。
本文提出的过滤式多标记特征选择框架的基本思想是:首先单独计算每个特征t与各个类标c的CHI值,然后再根据得分统计方式决定每个特征的最终得分,最后将特征按照最终得分进行降序排列,并进行前向搜索得到特征子集。
下面为通过计算每个特征t与各个类标c的CHI值,并根据得分统计方式得到最终得分的公式:
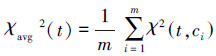 |
(2) |
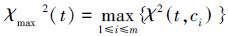 |
(3) |
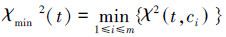 |
(4) |
式中m为类标个数。式(2)表示特征与各类标的平均CHI值作为该特征的最终得分;式(3)表示选取特征与各类标CHI值中的最大值作为该特征的最终得分统计;式(4)表示选取特征与各类标CHI值中的最小值作为该特征的最终得分统计。
实验数据来自于MULAN网站上公开的多标记数据集, 数据集相关信息如表 1所示。
| 数据集 名称 | 所属 领域 | 样本 个数 | 属性 个数 | 类标 个数 |
| emotions | 音乐 | 593 | 72 | 6 |
| medical | 文本 | 978 | 217 | 20 |
| Scene | 图像 | 2407 | 249 | 6 |
| yeast | 生物 | 2417 | 103 | 14 |
实验采用5种常用的多标记学习评价指标[9],对多标记数据特征选择之后的分类性能进行评价:排名损失、汉明损失、差一错误、覆盖范围、平均查准率。以上5种评价指标中,前4种评价指标的值越小,最后1种评价指标的值越大,表明性能越好。
实验采用10轮10倍交叉验证方法,即将实验数据随机平均分成10份,每次将1份作为验证集,其余9份整体作为训练集,不重复进行10次实验,统计其平均结果,作为实验最终结果。
通过将预处理后的多标记数据集利用卡方检验准则,可以分别得到每个特征t对应的各个类标c的CHI值。然后,按照不同的得分统计方式得到每个特征的最终得分,最后根据每个特征的最终得分,将全体特征做降序排列,使用前向搜索依次选取前n个特征(n=1, 2, …)作为特征子集。
max指的是选取利用卡方检验准则得到的每个特征对应各个类标所有CHI值的最大值,作为该特征的最终得分,进行特征排序。
avg指的是选取利用卡方检验准则得到的每个特征对应各个类标所有CHI值的平均值,作为该特征的最终得分,进行特征排序。
min指的是选取利用卡方检验准则得到的每个特征对应各个类标所有CHI值的最小值,作为该特征的最终得分,进行特征排序。
在将处理好的特征进行排序后,多标记分类器将利用搜索到的特征子集去完成分类任务。为了更加客观地测试特征子集的分类效果,实验选取了3个多标记分类器,分别是BR [10]、CC[11]和MLkNN[12]。
3 实验结果及分析按照上节的实验设置,在4个公开数据集上先进行特征选择,再分类,实验结果做如下分析。
3.1 Emotions数据集上的实验结果分析如图 1(其中横轴坐标表示特征子集所含有的特征个数,纵轴坐标表示特征子集在相应指标下的实验结果数值,之后分析相同)和表 2所示,在BR分类器下,随着特征个数增多到最后阶段3种得分统计方式搜索到的特征子集性能较差。虽然开始在min下搜索到的特征子集相比于其他2种方式,在5种评价指标下性能较差,但是随着特征个数的增加,min下的实验结果渐渐超过avg和max,最终达到全局最优,得到最优特征子集。而且avg和max下搜索得到的特征子集除了在差一错误评价指标下的实验结果存在较明显差异,在其余4种评价指标下预测结果差异较小。同时,可以看出在CC分类器下,整体趋势与BR分类器下相似,但是后期波动较小。在MLkNN分类器下,整体趋势与BR分类器下相似,但是后期波动较大。

|
| 图 1 Emotions数据集部分实验结果 Fig. 1 Partial results of the experiment on the emotions dataset |
| 分类器 | 得分 方式 | 排序 损失 | 汉明 损失 | 差一 错误 | 覆盖 范围 | 平均 查准率 |
| BR | max | 0.1931 | 0.2211 | 0.3220 | 1.9324 | 0.7657 |
| avg | 0.1939 | 0.2209 | 0.3237 | 1.9423 | 0.7656 | |
| min | 0.1738 | 0.2088 | 0.3001 | 1.8350 | 0.7849 | |
| CC | max | 0.1991 | 0.2316 | 0.3304 | 1.9290 | 0.7608 |
| avg | 0.1991 | 0.2305 | 0.3288 | 1.9524 | 0.7640 | |
| min | 0.1796 | 0.2105 | 0.3118 | 1.8381 | 0.7810 | |
| MLkNN | max | 0.2260 | 0.2448 | 0.3625 | 2.0714 | 0.7395 |
| avg | 0.2197 | 0.2450 | 0.3505 | 2.0529 | 0.7451 | |
| min | 0.2057 | 0.1977 | 0.3456 | 1.9716 | 0.7535 |
3.2 Medical数据集上的实验结果分析
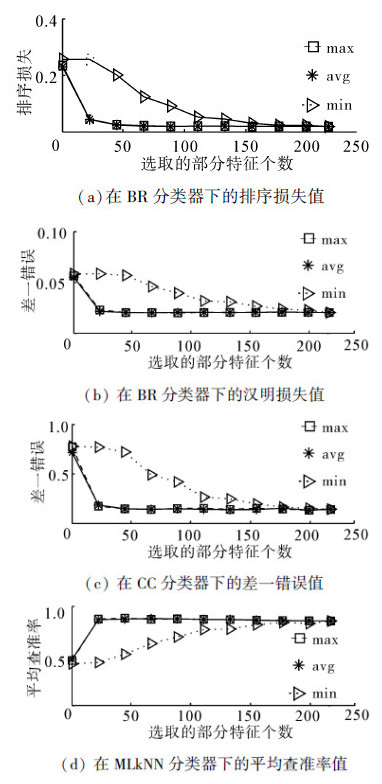
如图 2和表 3所示,在BR分类器下,avg和max 2种得分统计方式搜索到的特征子集在5种评价指标下预测结果差异较小,几乎重叠在一起。但是从全局最优结果看,在排序损失和覆盖范围指标下,avg和max都能搜到最优特征子集,而在汉明损失和差一错误指标下,avg结果最好,在平均查准率指标下,max结果最好。在min下搜索到的特征子集在5种评价指标下结果最差,而且收敛速度明显慢于avg和max,特征选择对于分类性能提升效果较差。同时,可以看出在CC分类器下,整体趋势与BR分类器下相似。但是从全局最优结果看,在5种指标下,max下搜索到最优特征子集,结果最好。在MLkNN分类器下,整体趋势与BR分类器下相似。
|
| 图 2 Medical数据集部分实验结果 Fig. 2 Partial results of the experiment on the medical dataset |
| 分类器 | 得分 方式 | 排序 损失 | 汉明 损失 | 差一 错误 | 覆盖 范围 | 平均 查准率 |
| BR | max | 0.0187 | 0.0196 | 0.1244 | 0.5697 | 0.9174 |
| avg | 0.0187 | 0.0195 | 0.1170 | 0.5697 | 0.9165 | |
| min | 0.0188 | 0.0202 | 0.1298 | 0.5707 | 0.9148 | |
| CC | max | 0.0207 | 0.0186 | 0.1266 | 0.6219 | 0.9147 |
| avg | 0.0229 | 0.0188 | 0.1277 | 0.6482 | 0.9119 | |
| min | 0.0244 | 0.0199 | 0.1373 | 0.6851 | 0.9067 | |
| MLkNN | max | 0.0309 | 0.0204 | 0.1360 | 0.8051 | 0.9014 |
| avg | 0.0359 | 0.0225 | 0.1645 | 0.9189 | 0.8806 | |
| min | 0.0417 | 0.0294 | 0.2088 | 1.0344 | 0.8535 |
3.3 Scene数据集上的实验结果分析
如图 3和表 4所示,在BR分类器下,3种得分统计方式搜索到的特征子集在5种评价指标下预测结果差异较小,几乎重叠在一起。但是从全局最优结果看,在排序损失指标下,3种得分统计方式达到相同结果,在汉明损失,覆盖范围和差一错误指标下,min结果最好,在平均查准率指标下,max结果最好。同时,可以看出在CC分类器下,整体趋势与BR分类器下相似。但是从全局最优结果看,在5种指标下,avg下搜索到最优特征子集,结果最好。在MLkNN分类器下,整体趋势与BR分类器相似。但是从全局最优结果看,在5种指标下,min下搜索到最优特征子集结果最好。

|
| 图 3 Medical数据集部分实验结果 Fig. 3 Partial results of the experiment on the medical dataset |
| 分类器 | 得分 方式 | 排序 损失 | 汉明 损失 | 差一 错误 | 覆盖 范围 | 平均 查准率 |
| BR | max | 0.0752 | 0.0970 | 0.2302 | 0.4595 | 0.8642 |
| avg | 0.0752 | 0.0973 | 0.2326 | 0.4595 | 0.8629 | |
| min | 0.0752 | 0.0968 | 0.2088 | 0..4590 | 0.8629 | |
| CC | max | 0.0871 | 0.0984 | 0.2584 | 0.5184 | 0.8461 |
| avg | 0.0839 | 0.0973 | 0.2555 | 0.5010 | 0.8493 | |
| min | 0.0856 | 0.0984 | 0.2584 | 0.5114 | 0.8462 | |
| MLkNN | max | 0.0769 | 0.0847 | 0.2235 | 0.4711 | 0.8669 |
| avg | 0.0766 | 0.0843 | 0.2231 | 0.4707 | 0.8674 | |
| min | 0.0749 | 0.0834 | 0.2119 | 0.4611 | 0.8716 |
3.4 Yeast数据集上的实验结果分析
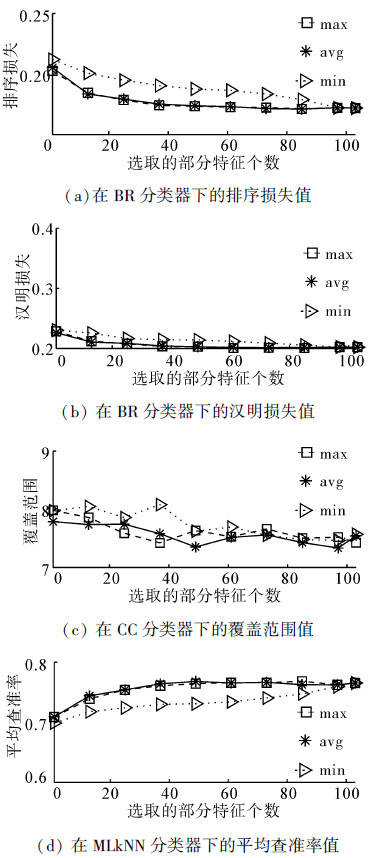
Yeast数据集部分实验结果如图 4所示。
|
| 图 4 Yeast数据集部分实验结果 Fig. 4 Partial results of the experiment on the yeast dataset |
在BR分类器下,avg和max两种得分统计方式搜索到的特征子集在排序损失、汉明损失和平均查准率指标下预测结果差异较小,几乎重叠在一起,但是在差一错误和覆盖范围指标下,都出现不同程度的小幅震荡。在min下搜索到的特征子集在5种评价指标下结果最差,而且收敛速度明显慢于avg和max,特征选择对于分类性能提升效果较差。从全局实验结果看,avg下搜索到的特征子集,达到最优结果。同时,可以看出在CC分类器下,3种取值方式搜索到的特征子集,在5种评价指标下的结果,都呈现出震荡的形式,尤其是在差一错误指标下,震荡幅度最大。虽然在震荡中,但是随着特征个数的增加,结果逐渐改善,说明特征选择起到了很好的提高分类性能的作用。从全局实验结果看,在排序损失和平均查准率指标下,avg下搜索到的特征子集表现最好,而且其余3种评价指标下,max下搜索到的特征子集表现最好。在MLkNN分类器下,整体趋势与在BR分类器下相似。从全局实验结果看,除了在排序损失和差一错误指标下,avg与max下搜索到的特征子集,达到相同最优结果,其余3种评价指标下,max的结果最好。Scene数据集实验的最优结果比较如表 5所示。
| 分类器 | 得分 方式 | 排序 损失 | 汉明 损失 | 差一 错误 | 覆盖 范围 | 平均 查准率 |
| BR | max | 0.0752 | 0.0970 | 0.2302 | 0.4595 | 0.8642 |
| avg | 0.0752 | 0.0973 | 0.2326 | 0.4595 | 0.8629 | |
| min | 0.0752 | 0.0968 | 0.2088 | 0..4590 | 0.8629 | |
| CC | max | 0.0871 | 0.0984 | 0.2584 | 0.5184 | 0.8461 |
| avg | 0.0839 | 0.0973 | 0.2555 | 0.5010 | 0.8493 | |
| min | 0.0856 | 0.0984 | 0.2584 | 0.5114 | 0.8462 | |
| MLkNN | max | 0.0769 | 0.0847 | 0.2235 | 0.4711 | 0.8669 |
| avg | 0.0766 | 0.0843 | 0.2231 | 0.4707 | 0.8674 | |
| min | 0.0749 | 0.0834 | 0.2119 | 0.4611 | 0.8716 |
3.5 实验结果
从以上所有实验结果可以看出,针对不同类型的多标记数据集,都有其特定的得分统计方式能很快地搜索到较优的特征子集,然后趋于稳定,说明特征选择起到了很好的提高分类性能的作用。为了便于使展示图片美观易懂,画图时特征子集所含特征个数采用间隔选取再绘制(本身实验数据是全的),所有的同类型图片都采用这个方法。
4 结束语本文提出过滤式的多标记特征选择框架,并使用卡方检验作为特征评价准则,在多个多标记数据集和分类评价准则上显示特征选择有助于提高多标记学习器的学习效果。本文通过对卡方检验得分的统计计算出每个特征的最终排序情况,选取了最大、平均、最小3种统计方式分别进行了实验比较。实验结果表明,利用本文框架采取不同的得分统计方式,对于不同类型的多标记数据集有不同效果。过滤式多标记特征选择框架还有一些问题有待进一步解决,比如如何在得分统计中加入衡量类标间的关系,如何采取更有效得分统计方式将提升特征子集在分类器下的分类效果等。
| [1] | TSOUMAKAS G, KATAKIS I, VLAHAVAS I. Mining Multi-label Data[R]. Data Minging and Knowledge Discovery Handbook, 2010: 667-685. |
| [2] | TSOUMAKAS G, KATAKIS I. Multi-label classification: an overview[J]. International Journal of Data Wareh-ousing and Mining , 2007, 40 (3) : 1-13 |
| [3] | ZHANG M L, ZHANG K. Multi-label learning by exploiting label dependency[C]//Proceedings of the 16th ACM SIG-KDD International Conference on Knowledge Discovery and Data Mining. Washington, DC, USA, 2010: 999-1008. |
| [4] | YANG Y, PEDERSEN J O. A comparative study on feature selection in text categorization[C]//Machine Learning International Workshop then Conference. Philadelphia, USA, 1997: 412-420. |
| [5] | SWATI S, GHATOL A, ASHOK C. Feature selection for medical diagnosis: Evaluation for cardiovascular diseases[J]. Expert Systems with Applications , 2013, 40 (10) : 4146-4153 DOI:10.1016/j.eswa.2013.01.032 |
| [6] | NEWTON S, EVERTON A C, MARIA C M, et al. A comparison of multi-label feature selection methods using the problem transformation approach[J]. Electronic Notes in Theoretical Computer Science , 2013, 292 : 135-151 DOI:10.1016/j.entcs.2013.02.010 |
| [7] | 计智伟, 胡珉, 尹建新. 特征选择算法综述[J]. 电子设计工程 , 2011, 19 (9) : 46-51 JI Zhiwei, HU Ming, YIN Jianxin. A survey of feature selection algorithm[J]. Electronic Design Engineering , 2011, 19 (9) : 46-51 |
| [8] | 邱云飞, 王威, 刘大有, 等. 基于方差CHI的特征选择方法[J]. 计算机应用研究 , 2012, 29 (4) : 1301-1303 QIU Yunfei, WANG Wei, LIU Dayou, et al. CHI feature selection method based on variance[J]. Application Research of Computers , 2012, 29 (4) : 1301-1303 |
| [9] | ZHANG M L, ZHOU Z H. A review on multi-label learning algorithms[J]. IEEE Transactions on Knowledge and Data Engineering , 2013, 39 (10) : 1-43 |
| [10] | MATTHEW R B, LUO J B, SHEN X P, et al. Learning multi-label scene classification[J]. Pattern Recognition , 2004, 37 (9) : 1757-1771 DOI:10.1016/j.patcog.2004.03.009 |
| [11] | READ J, PFAHRINGER B, HOLMES G, et al. Classifier chains for multi-label classification[J]. Machine Learning , 2011, 85 (3) : 333-359 DOI:10.1007/s10994-011-5256-5 |
| [12] | ZHANG M L, ZHOU Z H. ML-kNN: a lazy learning approach to multi-label learning[J]. Pattern Recognition , 2007, 40 (7) : 2038-2048 DOI:10.1016/j.patcog.2006.12.019 |



