2. 重庆邮电大学 计算机科学与技术研究所,重庆 400065
2. Institute of Computer Science and Technology, Chongqing University of Posts and Telecommunications, Chongqing 400065, China
人脸识别是模式识别中的一个经典问题,多年来一直是研究的热点。涌现出了许多经典的人脸识别算法,详见文献[1],这些方法在一般情况下能够实现取得较好的识别效果,但在光照、遮挡、面部伪装等情况下,识别性能急剧下降。最近,压缩感知[2]技术作为一个强有力的理论工具,已经被成功应用于图像处理领域[3]。Wright等[4]首次将压缩感知理论用到人脸识别中来,并提出了一种基于稀疏表示的分类器方法(sparse representation based classification,SRC),取得了非常好的人脸识别效果,特别在光照、遮挡、伪装的情况下,SRC具有很好的鲁棒性。基于稀疏表示的人脸识别是用已知的人脸图像构造训练字典,再将待识别的图片表示成字典原子的线性组合,然后根据线性组合系数来对测试样本进行重构,根据重构误差进行分类识别。基于稀疏表示的人脸识别方法的关键是对稀疏表示系数向量的求解,用稀疏向量中非零或权值较大的元素在训练样本集中的对应的向量来表示测试样本,从而根据表示误差来确定测试样本类别归属,识别原理如图 1所示。

|
| 图 1 稀疏表示人脸识别示意图(误差未知) Fig. 1 Schematic diagram of face recognition with sparse representation (unknown residual) |
这种在大量样本中选择一部分符合要求的少量样本是统计学里的变量选择过程。在大量的数据中,可能只需要少量的数据,如何从大量的数据中选择出少量有用的数据是变量选择的基本任务。基于线性表示的变量选择模型的误差是不可知的如图 1所示,SRC采用的是对一个线性回归模型及其残差用“残差函数+似然估计”的稀疏约束方式,首先假设残差服从一种特定的分布,然后再对其进行极大似然估计,但这种对残差似然估计不能准确地反映残差的真实情况,特别是在残差模型不可预知的情况下,根本无法进行似然估计。Candes和Tao于2007年提出了一种新的变量选择模型(Dantzig selector,DS)[5],DS模型不依赖于一个对残差特定的似然估计,通过矩阵相关性和L∞范数代替残差函数特定分布的似然估计,并结合L1范数进行稀疏约束,使回归模型处理残差时更方便,适用性更强。本文将Dantzig selector模型的变量选择方法用于人脸识别。
1 线性表示模型首先介绍一个标准经典线性回归模型:
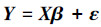 |
式中:Y=[y1 y2…yn]T是一个n×1维的响应向量,X=[x1 x2…xp]是一个n×p维的设计矩阵,xi, i=1, 2, …, p是一个n×1维的列向量,β=[β1 β2…βp)T是一个p维的未知回归系数向量,ε是一个n维的误差向量,称之为残差,传统的线性回归方法可见文献[6]。最简单的回归模型是最小二乘(least square,LS),它的基本思想是求β,使得残差平方和达到最小,即
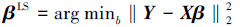 |
式中:‖.‖2表示矩阵的L2范数。Boyd在《Convex optimization》[7]一书中指出,这种基于L2范数依赖于依赖于残差服从于Gauss分布一个极大似然估计。在此基础上,研究者采用“残差函数+似然估计”的思路,提出了2种新的约束模型:岭回归和LASSO模型。
1.1 岭回归模型岭回归(ridge regression)方法思想可以看成是在最小二乘法的基础上对回归系数加以控制,定义式为
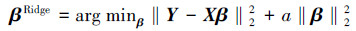 |
a是一个大于零的调节参数,基于该模型,Zhang等[8]提出一种基于最小二乘约束协同表达分类方法(collaborative representation classification based on regularized least square, CRC-RLS)。作者深入分析了协同表达在分类中的作用原理,指出SRC是协同表达的一种特殊形式,并将其用于人脸识别,他们把测试样本看作是所有训练样本的协同表达结果,通过协同表达系数进行分类。
1.2 LASSO模型Tibshiran[9]提出了最小绝对值收缩和选择算子(least absolute shrinkage and selection operator,LASSO),可以看作是L1惩罚函数下的最小二乘估计,LASSO的定义式为
 |
式中:‖.‖1表示L1范数,a是一个大于零的调节参数。文献[4]中的SRC算法的核心在于利用了LASSO模型在训练样本字典中选择少量的样本来表示测样本。LASSO的模型没有解析解,它利用了L1范数约束方程,将回归模型的复杂求解转换成凸优化问题的线性规划来来求解。此外,研究者们提出了许多算法,Yang等在文献[10]中对LASSO的几种快速有效的求解方法进行了综述,该文献还指出对于鲁棒人脸识别,同伦算法[11]相对于其他的方法在获得很好计算精度的同时所需的时间复杂度低,因此本文实验部分采用同伦算法来求解LASSO模型。
1.3 DS(Dantzig selector)模型以上对L2范数约束模型都依赖于残差服从于Gauss分布一个极大似然估计,不同于以上基于最小二乘的正则化约束的变量选择方法,Dantzig selector不依赖于一个特定的似然函数,定义如下:
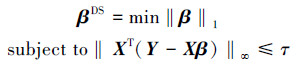 |
(1) |
式中:‖.‖∞表示L∞范数,τ>0是一个调节参数。约束的变量是残差相关向量XT(Y-Xβ)而不是残差向量Y-Xβ,主要是基于以下方面考虑:相关残差具有正交变换不变性,而残差没有这种性质,假设U是一个正交矩阵,则有(UX)T(UY-UXβ)=XT(Y-Xβ)。另一方面相关残差有助于选取与响应向量Y高度相关性的变量。它的一个主要的优点是不依赖于一个特定似然函数,使它的应用范围更广阔些,更适应于样本量很大的情况。式(1)可以转化成一个凸优化过程,并通过线性规划(Linear programming, LP)[12]有效地求解,但是对一个n×p线性系统,线性规划求解式(1)时间复杂度是O(p3)。Asif[13]提出一种了原始-对偶追踪算法(Primal Dual Pursuit, PD-Pursuit),其基本思路与同伦算法相同,本文运用PD-Pursuit算法求解DS模型。
1.4 DS模型 1.4.1 DS模型的对偶形式DS模型对一些给定的τ>0,PD-Pursuit算法利用DS模型原始和对偶目标函数的强对偶性,首先给出DS模型的对偶形式,对于任意一个经定的τ,推导出其原始解和对偶形式的解必须要满足的优化条件。最终通过改变τ的值,可以建立起DS模型的解。式(1)的对偶形式定义为
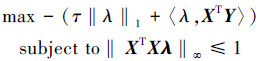 |
(2) |
式中:λ∈Rp是一个对偶向量, 对应于式(1)的原始向量β,〈·〉表示向量内积,利用原始目标函数和对偶目标函数的强对偶性,假设在任意次优化过程中,存在一对原始对偶解(β*, λ*),可以得到如下等式:
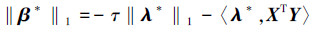 |
又可以等价为
 |
(3) |
由互补松弛条件可知:对于任意一对原始-对偶解,对偶向量非零,相应的原始向量对应于式(1)同伦路径的支撑集。因此,式(1)、(2)的可行性条件为
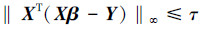 |
(4) |
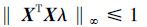 |
(5) |
对于任意一个给定的τ可以得到原始-对偶解(β*, λ*)必须要满足的4个优化条件:
1)XΓλT(Xβ*-Y)=τzλ
2)XΓλTXλ*=-zβ
3)|xγT(Xβ*-Y)| < τγ∈Γλ
4)|xγTXλ*| < 1γ∈Γβ
Γβ、Γλ分别是β*、λ*的支撑集,zβ、zλ分别是β*、λ*在各自支撑集下的符号,其值为±1或0,x表示活动集下对应的X子集,在任意给定τ值,一对原始-对偶解(β*,λ*)在它的支撑集和符号序列下, 1)~4)是该解惟一的充分必要条件。因此求式(1)可以转化为求满足1)~4)一对原始-对偶解。
同伦算法是沿着一些变化了的同伦参数不断优化解的路径的过程,首先假设一个初始化的解,通过改变同伦参数实现迭代来达到所期望的解。在PD-Pursuit中,把τ看作是一个同伦参数,假设k∈{1, 2, …}表示同伦迭代过程的索引号, 第k次迭代时τ的值为τk, 对应于一对原始对偶解(βk, λk), PD-Pursuit可以看作是随着参数τ的变化,不断减少τ到第k次迭代时减少到一个初始给定的值, 沿着第k次迭代的一组解(βk, λk)到最终解(β*, λ*)所经过的路径。从条件(K1~K4)不难得出,对于第k次迭代,(Γλ,Γβ,zλ,zβ)共同确定式(1)模型的解,可以描述成如下等式:
 |
(6) |
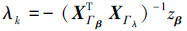 |
(7) |
在PD-pursuit中,在τ减少至一个给定的值之前,利用条件(K1-K4)不断地同时更新原始和对偶向量,沿着这个同伦路径,有一些引起原始、对偶向量的支撑集发生改变的τ的临界值。因此,该算法的本质上是沿着这些临界值改变原始、对偶向量不断更新的同伦路径变化的过程。PD-pursuit主要可以分为2个部分:原始更新和对偶更新。在原始更新阶段,利用式(6)的原始可行性条件更新原始向量,在对偶更新阶段选用式(7)的对偶可行性条件更新对偶向量, 下面分别讨论2种更新。
1.4.2 原始向量更新同伦算法的更新包括了方向和该方向上的路径的更新, 对于原始向量可以表示为:βk+1=βk+δ∂β,δ>0。从0开始不断地增加δ的值,原始的约束也会发生改变,这种变化可以分为2种情况:新的元素进入集合Γλ所有的活动约束也会随着δ的大小改变而收缩。根据式(6)所求得的βk,联合定义式(8)求解δ。
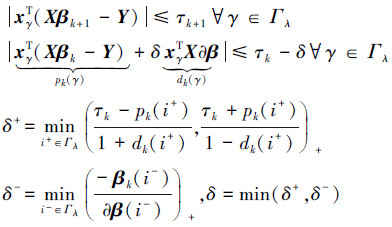 |
(8) |
式中:min(.)+表示只接收正数并取最小的一个。其中i+、i-分别表示δ+、δ-所对应的索引号。如果δ+ < δ-,新的索引号i+进入索引集Γλ,否则i-留在Γβ相应的符号zβ更新,同伦参数变成τk+1=τk-δ。
1.4.3 对偶向量更新同理对于对偶向量,可以假设λk+1=λk+θ∂λ,θ>0,根据式(7)求得的λk联合定义式(9)可以求θ。
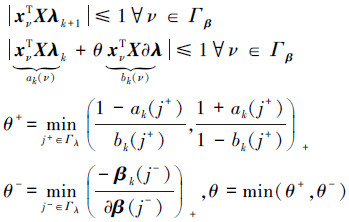 |
(9) |
式中j+、j-分别表示θ+、θ-所对应的索引号。如果θ+ < θ-,新的索引号j+进入索引集Γβ,否则j-留在Γλ相应的符号zλ更新。
1.4.4 方向更新假设在一个参数τk下可以得到一对原始对偶解(βk,λk),其支撑集和符号用(Γλ,Γβ,zλ,zβ)来表示。根据(K1~K4)的优化条件可以推导出原始向量和对偶向量的方向更新。对原始向量βk,在∂β方向上使得τk减少最大。利用(K1)可以得到βk的更新方向∂β:
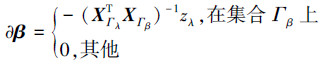 |
(10) |
对于对偶向量的更新方向∂λ,首先假设在原始更新阶段一个新的索引λ进入集合Γλ,利用原始更新的附加条件和条件(K2),可以得到λk的更新∂λ:
 |
(11) |
式中:xγ表示集合X的第γ列,zγ表示第γ个原始活动约束的符号。
综上所述,可以得到PD-Pursuit算法的伪代码如下:
原始-对偶算法:
给定一个迭代停止条件τ,当k=1时,初始化:
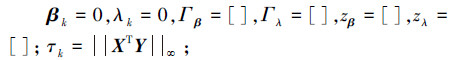 |
repeat:
k←k+1原始更新:
根据式(8)、(10)计算pk、dk、δ、∂β
βk+1=βk+δ∂β, τk+1=τk-δ;
If δ=δ-then
Γβ←Γβ\i-将i-从Γβ中移去并更新Γβ;
Γλ←Γλ\γ选择一个索引号γ并从Γλ移出;zγ=zλ(γ);
更新zλ、zβ;
Else
Γλ=Γλ∪{i+}把i+存入Γλ但不更新Γλ;
zλ=sign[XΓλT(Xβk+1-Y)];
γ=i+;
zγ=zλ(γ);
End if
对偶更新:
根据式(9)、(11)计算∂λ、ak、bk
If δ=δ- & sign [ak(i-)]=sign [bk(i-)]then
∂λ←-∂λ;
bk←-bk;
End if
根据式(9)计算θ
λk+1=λk+δ∂λ;
If θ=θ-then
Γλ←Γλ\j-将索引j-从Γλ中移去更新Γλ;
更新zλ;
Else
Γβ←Γβ∪{j+}把j+存入Γβ并更新Γβ;
zβ=sign[XΓβT Xλk+1];
End if
直到τk+1≤τ停止迭代。
上述算法的主要的时间复杂度来自于更新方向Γλ、Γβ以及∂λ、∂β和沿该方向的更新路径长度δ、θ。每一步计算中都要计算一个方阵XΓβTXΓλ和它的逆矩阵。因为该算法是每一次在原集合添加或移去一个元素,因此每一次计算的时候都不需要整个线性系统都计算。对于一个维数为n×p的矩阵X,假设第k步支撑集的长度是Sk,Sk≪p,每一次计算复杂度为O(Sk3+Sk3n),对于XΓβTXΓλ的求逆,由矩阵求逆的原理可知每一次计算的复杂度为O(Skm)。对于路径更新长度来说每一次的计算时间复杂度为O(np)。综上分析,每一步的计算只是一些矩阵和向量的乘法运算,通常对一个线性系统而言,每一个矩阵和向量的长度是一样的,因此,每一步的时间复杂度都是一样的,假设共进行了d次同伦迭代,上述算法的总的时间复杂度为O(dnp),远小于LP的时间复杂度O(p3)。
2 基于模型的人脸识别算法假设x∈Rn×1表示一个训练样本,第i类共pi个训练样本Xi=[x1 x2 … xpi]∈Rn×pi,有k类共有p样本, X=[X1 X2 … Xp]∈Rn×p称为训练字典,测试样本Y∈Rn×1。采用文献[5]相同的稀疏分类策略,可以得到基于DS模型人脸识别分类算法(Dantzig selector based sparse representation classification, DS-SRC)的实现步骤如下:
1)归一化X的每一列和Y;
2)利用PD-Pursuit算法求解式(5)的稀疏解β;
3)计算每一类训练样本上的重构误差:
 |
4)根据重构误差判断测试样本的类别:
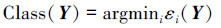 |
为了验证本文中基于DS模型的人脸识别算法的性能,本文在常用的Extend Yale B人脸库[14]和AR人脸库[15]进行实验。所有实验均在主频2.10 GHz,内存为4 GB的Acer笔记本上完成,用MATLAB实现。
3.1 Extend Yale B人脸库的实验Extended Yale B人脸库由38个不同的个体共2 414张正面人脸图像组成。这些图像是在不同的光照条件下采集的,图 2是该库的人脸图像。样本的原始大小为192×168, 实验中,所有的图像进行剪裁和归一化到64×56的统一分辨率。与文献[4]的实验方案一样, 本文实验中也对每个不同的个体随机选取一半的人脸作为训练样本,剩下的样本作为测试样本。所有样本按列连接成一个列向量大小为3 584维, 构成了一个3 584×1 207维的训练字典,对于这样一个高维度的矩阵而言,计算量非常大,因此,实验采用文献[16]将样本的维数(每一列的维数)分别降至30维、54维、120维、300维和504维的情况下,与目前传统的最近邻分类器(nearest neighbor, NN)[17]基于Lasso模型稀疏表示的人脸识别算法SRC[4]以及CRC-RLS[8]进行对比,其中CRC-RLS采用作者公布代码(http://www4.comp.polyu.edu.hk/~cslzhang/code/)。实验中,SRC算法中Lasso模型参数选取α=1E-3, PD-Pursuit算法迭代停止条件选取τ=lE-5。

|
| 图 2 Extended Yale B人脸库图像 Fig. 2 Face image of Extended Yale B face database |
实验结果如表 1所示,从表中可以得到如下结论:在各种给定的特征维数下,DS-SRC的识别率均高于SRC;基于稀疏表示框架的识别方法相对于最近邻分类的方法优势明显。该库的人脸图像包含的光照变化较多,因此,本文采用的人脸识别模型对光照具有很好的鲁棒性。
| 维数 | NN | SRC | CRC-RLS | DS-SRC |
| 30 | 0.645 4 | 0.881 5 | 0.733 7 | 0.883 2 |
| 54 | 0.803 4 | 0.929 9 | 0.872 3 | 0.931 6 |
| 120 | 0.863 6 | 0.964 1 | 0.954 1 | 0.967 4 |
| 300 | 0.903 0 | 0.968 3 | 0.964 1 | 0.977 4 |
| 504 | 0.909 2 | 0.966 6 | 0.977 5 | 0.986 6 |
3.2 AR人脸库上的实验
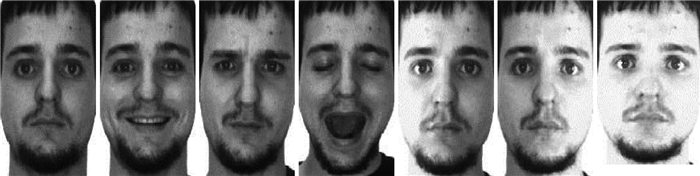
AR人脸库包含了126个不同个体,每个不同个体采集了26张正面人脸图像分辨率为165×120,人脸图像在不同的光照条件,表情变化,以及脸部遮挡,墨镜等面部伪装的情况下采集,部分样本如图 3所示。实验中每张图像经过归一化处理为60×43的统一分辨率。
|
| 图 3 AR人脸库图像 Fig. 3 Face image of AR face database |
AR人脸库较之于Extend Yale B人脸库难度增加了,除了光照变化外,还有表情的变化,此外,每一类的训练样本量减少的同时类别数却增加。实验中选取它达到一个子集,子集中包含了100个个体,其中男女各个50人共1 400张人脸图像,随机选取其中7张作为训练集,其他作为测试样本。所有样本按列连接成一个列向量大小为2 580维, 构成的训练字典大小为2 580×700维,与上一个实验一样,同样进行PCA降维至30维、54维、120维、300维和504维,参数和上一个实验设定一样,进行几种方法的识别率比较。实验结果如表 2。可以看出,本文方法在各种维数下比SRC识别效果要好,本文模型对表情变化也具有很好的鲁棒性。
| 维数 | NN | SRC | CRC-RLS | DS-SRC |
| 30 | 0.6205 | 0.7282 | 0.6438 | 0.7382 |
| 54 | 0.6777 | 0.8169 | 0.8026 | 0.8212 |
| 120 | 0.7034 | 0.8913 | 0.9041 | 0.9070 |
| 300 | 0.7131 | 0.9056 | 0.9255 | 0.9285 |
| 504 | 0.7230 | 0.9099 | 0.9216 | 0.9227 |
3.3 图像遮挡和噪声的鲁棒性实验
基于稀疏表示的人脸识别方法重要的特点是对噪声和遮挡鲁棒性,遮挡和噪声的线性表示模型如图 4、5所示。图 4和5中,子图(a)表示受到噪声干扰或遮挡影响的图像,子图(b)表示假设理想线性表示图像,子图(c)表示未知分布的表示残差。在文献4中,作者在原来训练字典中引入一个单位矩阵来实现对噪声的编码,而本文则直接采用DS模型,不进行特殊编码。选取Extended Yale B人脸库的子集1和子集2共719张正面人脸图像作为训练样本集,子集3的455张正面人脸图像作为测试集。对于遮挡实验,用一张不相关的图像去遮挡对每一个训练样本,遮挡位置不确定,遮挡图像占整个图像的比例从10%~50%, 如图 6所示。在噪声鲁棒性实验中,对每一个训练样本分别添加10%~90%的分布未知随机噪声, 如图 7所示。

|
| 图 4 遮挡线性表示示意图(误差未知) Fig. 4 Schematic diagram of linear representation for Occlusion (unknown residual) |

|
| 图 5 噪声线性表示示意图(误差未知) Fig. 5 Schematic diagram of linear representation for corruption (unknown residual) |

|
| 图 6 遮挡图像,依次为10%~50%遮挡比例 Fig. 6 Occlusion image, successively occluded 10%~50% |

|
| 图 7 噪声污染图像,依次为10%~90%噪声比例 Fig. 7 Noise image, successively noised 10%~90% |
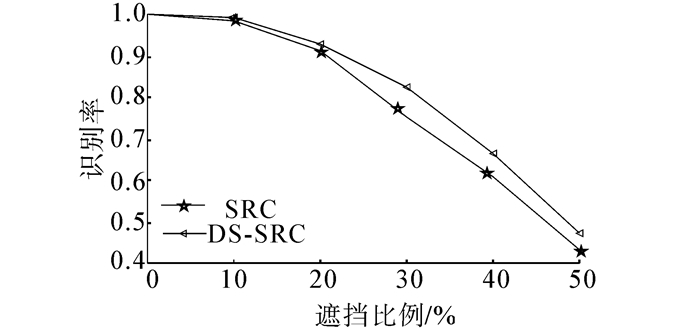
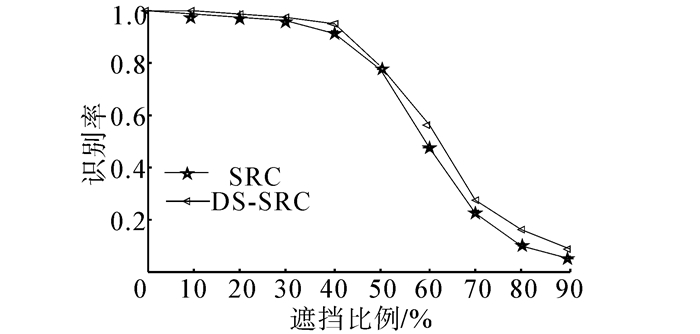
所有的样本都归一化到分辨率为64×56,所有的样本按列连接成一个列向量大小为3 582维,构成的训练字典大小为3 582×719。在这2个实验中,本文提出的方法只与文献[4]的方法进行对比,这是因为文献[4]的实验结果表明NN和CRC-RLS对噪声和遮挡的鲁棒性明显不强。相关参数设置与上2个实验一样,不同的是,为了不改变所加遮挡和噪声的真实特性,这里不对图像进行降维处理,直接对大小为3 582×719维的训练字典运用DS-SRC算法求解, SRC算法采用文献[4]的实验方法。从图 8、9可以看出, 本文方法在对噪声和遮挡具有较强鲁棒性。
|
| 图 8 遮挡鲁棒性实验结果 Fig. 8 Experiment Results of robust for occlusion |
|
| 图 9 噪声鲁棒性实验结果 Fig. 9 Experiment results of robust for noise |
DS模型利用了测试样本矩阵和线性表示残差的内积来表示同一个个体的训练样本之间的相关性进行约束。这种变量选择机制避免了基于最小二乘估计的特定的似然函数的假设。只关心测试样本和训练样本库中的相关性,而通常不管是在实验中还在实际应用中,训练样本都是经过严格预处理,因此不需要对残差进行类似于添加一个抗遮挡的噪声编码, 本文的方法在取得了比SRC加入噪声编码后更好的实验结果,说明本文所采用模型适应性更强。
4 结束语DS模型利用了测试样本矩阵和线性表示残差的内积来表示同一个个体的不同训练样本之间的相关度, 再利用L∞这种具有选择功能的矩阵的范数,选择出最大的相关度的训练样本出来,对其进行约束。这样一个相关性选择的思路即克服了传统线性模型对残差的特定似然估计的要求,使得线性模型更具有适用性,处理噪声更方便, 同时通过L1范数约束保证了解的稀疏性,便于分类。因此,在人脸识别中,即便是训练样本存在相似度较高的个体,也能通过相关度最大进行区分。测试图像有噪声污染等高难度的情况下,不需要特殊噪声编码,也能有效地进行识别,实验证明了本文提出的DS-SRC算法取得了良好的识别效果。
| [1] | ZHAO W, CHELLAPPA R, PHILLIPS P J, et al. Face recognition: a literature survey[J]. ACM Computing Surveys , 2003, 35 (4) : 399-458 DOI:10.1145/954339 |
| [2] | DONOHO D L. Compressed sensing[J]. IEEE Transactions on Information Theory , 2006, 52 (4) : 1289-1306 DOI:10.1109/TIT.2006.871582 |
| [3] | MAIRAL J, ELAD M, SAPIRO G. Sparse representation for color image restoration[J]. IEEE Transactions on Image Processing , 2008, 17 (1) : 53-69 DOI:10.1109/TIP.2007.911828 |
| [4] | WRIGHT J, YANG A Y, GANESH A, et al. Robust face recognition via sparse representation[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence , 2009, 31 (2) : 210-227 DOI:10.1109/TPAMI.2008.79 |
| [5] | CANDES E, TAO T. The Dantzig selector: statistical estimation when p is much larger than n[J]. The Annals of Statistics , 2007, 35 (6) : 2313-2351 DOI:10.1214/009053606000001523 |
| [6] | 王大荣, 张忠占. 线性回归模型中变量选择方法综述[J]. 数理统计与管理 , 2010, 29 (4) : 615-627 WANG Darong, ZHANG Zhongzhan. Variable selection for linear regression models: a survey[J]. Journal of Applied Statistics and Management , 2010, 29 (4) : 615-627 |
| [7] | BOYD S, VANDENBERGHE L. Convex optimization[M]. Cambridge: Cambridge University Press, 2004 . |
| [8] | ZHANG L, YANG M, FENG X C. Sparse representation or collaborative representation: which helps face recognition[C]//IEEE International Conference on Computer Vision. Barcelona, Spain, 2011: 471-478. |
| [9] | TIBSHIRANI R. Regression shrinkage and selection via the lasso[J]. Journal of the Royal Statistical Society , 1996, 58 (1) : 267-288 |
| [10] | YANG A Y, SASTRY S S, GANESH A, et al. Fast ℓ1-minimization algorithms and an application in robust face recognition: a review[C]//IEEE International Conference on Image Processing, Hong Kong, China, 2010: 1849-1852. |
| [11] | MALIOUTOV D M, CETIN M, WILLSKY A S. Homotopy continuation for sparse signal representation[C]//IEEE International Conference on Acoustics, Speech, and Signal Processing. NewYork, USA, 2005: 733-736. |
| [12] | CANDES E, TERENCE TAO. Decoding by linear programming[J]. IEEE Transactions on Information Theory , 2005, 51 (12) : 4203-4215 DOI:10.1109/TIT.2005.858979 |
| [13] | ASIF M S. Primal dual pursuit: A homotopy based algorithm for the Dantzig selector[D]. Atlanta: Georgia Institute of Technology, 2008. |
| [14] | GEORGHIADES A S, BELHUMEUR P N, KRIEGMAN D J. From few to many: illumination cone models for face recognition under variable lighting and pose[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence , 2001, 23 (6) : 643-660 DOI:10.1109/34.927464 |
| [15] | MARTINEZ A, BENAVENTE R. The AR face database [R]. Barcelona, Spain. 1998. |
| [16] | TURK M, PENTLAND A. Face recognition using eigenfaces[C] //IEEE Computer Society Conference on Proceedings in Computer Vision and Pattern Recognition. Hawaii, USA, 1991: 586-591. |



