波兰数学家Pawlak于1982年提出了粗糙集理论^[1]，它是一种处理模糊、不精确性以及不确定性的数学工具。近年来，由于它具有诸多优势，已经被成功地运用于数据挖掘、模式识别、数据处理、决策分析等领域^[2-4]。然而，在现实生活中，由于噪声、测量数据的不完整性等因素，不完备信息系统依然广泛存在。而Pawlak提出的经典粗糙集并不适用不完备信息系统。这就有必要对它进行扩充以适用于处理不完备数据。目前，针对不完备信息系统缺失值的不同理解，对经典粗糙集的扩充研究有如下模型：Kryszkiewicz^[5]提出了基于容差关系的粗糙集模型，把不完备信息系统中的缺失值看作是遗漏型的，即可以和任意的对象进行比较；Stefanowski等^[6]提出了基于非对称相似关系和量化容差关系的粗糙集模型，把不完备信息系统中的缺失值看作是缺席型的；为了克服扩展模型的不足，王国胤^[7]又给出了基于限制容差关系的粗糙集模型。这方面的更多研究，可以查看文献[8-10]。

在现实世界中，很多的信息系统其属性值域可能具有偏序性。此时，经典粗糙集方法显得无能为力。为了能够处理具有偏序关系的信息系统，Greco等^[11]提出了基于优势关系的粗糙集模型，即运用优势关系代替等价关系。为了让优势关系下的粗糙集模型能够同时处理缺失值，Shao等^[12]把不完备序信息系统中的缺失值看作是遗漏型的，提出了基于优势关系的不完备序信息系统，并讨论了属性约简和规则提取。针对文献[12]提出的优势关系过于宽松，容易将实际不满足条件的对象误判为同一个优势类，胡明礼等^[13]通过引入一个阈值得到了广义扩展优势关系的概念，并对规则提取进行了重新考虑。此外，针对优势系统中缺失值是缺席型的情况，杨习贝等^[14]提出了相似优势关系的粗糙集模型，并对属性约简做了研究。然而这并没有弥补文献[12]提出的优势关系过于宽松的缺陷，并且改进后的模型还容易将一些本属于同一决策类的对象误判为不同决策类。这在一定程度上会影响文献[12]提出的模型决策分析的效果。因此，Luo等^[15]进一步又给出了限制优势粗糙集模型，既可以避免文献[12]提出的优势关系过于宽松的现象，又不容易将一些本属于同一决策类的对象误判为不同的决策类。但文献[15]提出的限制优势关系在某些情况下又显得过于严格，例如：当2个对象在各属性下的取值为x=(4,3,2,1),y=(*,*,2,1)时，且各属性值域的最大值均为4，那么根据文献[15]提出的限制优势关系，对象x是不优于对象y的；可现实生活中，对象x优于对象y的可能性是非常大的，这有可能导致数据集中的决策规则没有充分提取。

基于此，本文在分析不完备序信息系统中现有的几种扩展粗糙集模型的基础上，提出了基于α优势关系的粗糙集模型，它既吸收了其他扩展模型的优点，又能有效克服它们的局限性，更有利于处理现实中的数据集。此外，基于α优势关系的粗糙集模型，给出了不完备序信息系统和序决策系统的区分矩阵属性约简算法，并表明了其区分矩阵只能运用属性集的幂集进行构造，而不能简单地运用单属性集进行构造。

1 基本概念

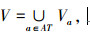
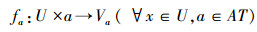
四元组IS=(U,AT,V,f)，其中U是非空有限的对象集合，AT是非空有限的属性集合，AT为条件属性集，且V_a是属性a的值域，满足，称四元组IS为一个信息系统。

若存在一个属性a∈AT使得V_a为空值(记作：f(x,a)=*)，则称该信息系统是不完备的信息系统，记作：IIS；否则称为完备的信息系统。

定义1^[11] 设IS=(U,AT,V,f)是一个完备信息系统，对于∀A⊆AT，∀x,y∈U，有：

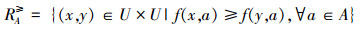则称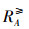为信息系统下的优势关系，满足这种关系的完备信息系统称之为序信息系统，记作：OIS。

记：

为对象x在序信息系统中的优势类，且。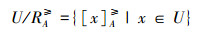

定义2^[12] 设IIS=(U,AT,V,f)是一个不完备信息系统，对于A⊆AT，∀x,y∈U，有

则称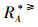是不完备信息系统上的一个优势关系，满足具有优势关系的不完备信息系统称之为不完备序信息系统，记作：IOIS。

通过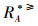的定义，显然可以看出，在条件属性集A下，对象x优于对象y。

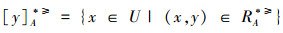
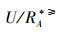
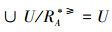
记： ，则描述的是：论域中的对象在条件属性A下，优于或者等于对象y的集合，简称为对象y的优势类。因此，中所有的优势类构成了论域U的覆盖，而不是论域U的划分，即。

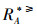
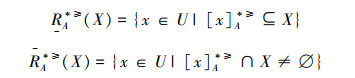定义3^[12] 设IOIS=(U,AT,V,f)是一个不完备序信息系统，∀X⊆U，A⊆AT，对象集合X在优势关系下关于属性集A∈AT的上下近似集为

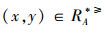
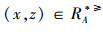
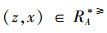
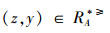
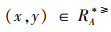
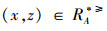
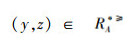
通过分析定义2，可以得出文献[12]在不完备序信息系统中提出的优势关系是以空值可以等于任意值为假设前提的，即认为空值可以优于任意值，同时又认为任意值可以优于空值，这显然不符合实际情况。例如：当x=(1,1,∗)，y=(1,1,4)，z=(∗,∗,4)时，其中“4”表示属性值下最大的取值，“1”为属性值下最小的取值。根据定义2进行分析可得： ，，，，，成立。然而事实上，缺失值∗优于属性值4以及属性值1优于缺失值∗的可能性是非常之小，但是属性值4优于缺失值∗以及缺失值优于属性值1必然成立。因此，，，成立的可能性是非常之小。这说明文献[12]提出的优势关系的划分粒度过大，容易把不属于优势类的对象归结到优势类中。针对文献[12]提出的不完备序信息系统粗糙集模型的缺陷，文献[15]提出了基于限制优势关系的粗糙集模型。

定义4^[15] 设IOIS=(U,AT,V,f)是一个不完备序信息系统，对于A⊆AT，∀x,y∈U，对象在属性集A下的限制优势关系为

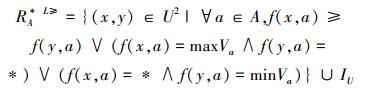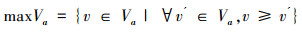
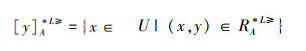
其中，，I_U是一个确定关系，I_U={(x,x)|x∈U}。因此，

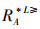
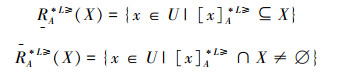定义5^[15] 设IOIS=(U,AT,V,f)是一个不完备序信息系统，∀X⊆U，A⊆AT，对象集合X在优势关系下关于属性集A⊆AT的上下近似集为

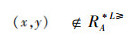
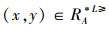
通过分析定义4提出的限制优势关系，可以得出文献[15]提出的限制优势关系过于严格，划分的粒度过细。例如：当x=(4,3,2,1),y=(∗,∗,2,1)时，其中“4”表示属性值下最大的取值，“1”为属性值下最小的取值。根据定义4分析可得： 。然而，事实上，的可能性是非常大。这说明文献[15]提出的限制优势关系划分的粒度过细，容易把一些本该属于优势类的对象误判为不是优势类的对象，这样容易导致提取决策规则的不完全性。基于此，在不完备序信息系统中，有必要提出一种相对于文献[12]提出的优势关系以及文献[15]提出的限制优势关系更加灵活的优势关系。

2 α优势关系的粗糙集模型

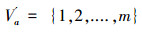
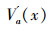
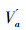
设IOIS=(U,AT,V,f)是一个不完备序信息系统，对于∀a⊆AT，∀x,y∈U，对象在属性a下的取值为V_a={a₁,a₂,....,a_m}，并且a₁₂ < ...m，根据V_a的排序，令a₁=1,a₂=2,...,a_m=m，则对象在属性a下的取值转变为，其中为对象x在中转化的值。

定义6 设IOIS=(U,AT,V,f)是一个不完备序信息系统，对于∀a⊆AT，∀x,y∈U，对象在属性a下的取值为V_a={a₁,a₂,...,a_m}，并且a₁₂ < ...m，则对象x在属性集a下优于y的概率为

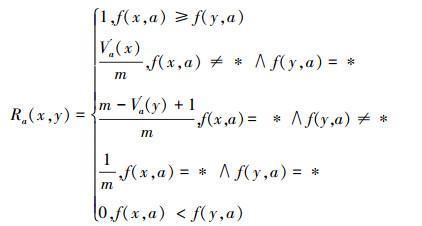从定义6中得知，在单属性下，2个对象优于的程度在0和1之间。当对象x在属性a下取值完全小于对象y的取值时，用数值0来表示对象x劣于对象y的程度，即概率；当对象x在属性a下取值完全大于对象y的取值时，用数值1来表示对象x优于对象y的程度。然而，当对象x和对象y有一个缺失值时，且对象在属性下取值的多样性，使得很难确定2个对象的优于程度；根据概率的含义，即在m个数中，有n个数优于一个确定数值的概率为n/m，得出定义6,2个对象中有一个为缺失值时它们的优于程度。当2个对象都为缺失值时，没有根据可以判别它们之间优于程度，因此，运用1/m概率来表示，意味着优于程度很小。

定义7 设IOIS=(U,AT,V,f)是一个不完备序信息系统，对于A⊆AT，∀x,y∈U，则对象x在属性集A下优于y的概率为

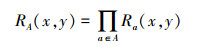通过定义7，可以得出不完备序信息系统各个对象的优势类如下：

定义8 设IOIS=(U,AT,V,f)是一个不完备序信息系统，对于A⊆AT，∀x,y∈U，有

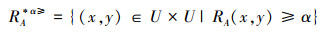则称是不完备序信息系统上的一个α优势关系，其中0<α≤1。

记： ，则描述的对象是：在条件属性集A下，以α的优势度优于对象y的最大对象的集合，简称为对象y的α优势类。由于表示所有与优势关系族相关的知识，记作，则中的任何一个元素都是属于α优势类。从而可以得知中所有的α优势类构成了U中的覆盖，而不是U中的划分，即。

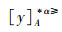
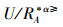
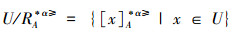
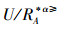
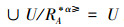
根据定义8，结合定义2和定义4的概念，显然可以得出：当α>0时，；当α=1时，。因此，在不完备序信息系统中，本文提出的α优势关系是文献[12]提出的优势关系和文献[15]提出的限制优势关系的一种扩展形式。

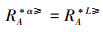
性质1 设IOIS=(U,AT,V,f)是一个不完备序信息系统，则α优势关系满足如下性质：

1) 满足自反性，不满足对称性和传递性；

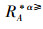
2)当B⊆A⊆AT时，；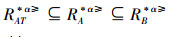

3)当B⊆A⊆AT时，∀x∈U，

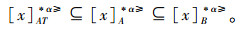性质2 设IOIS=(U,AT,V,f)是一个不完备序信息系统，对于A⊆AT，、 、 三者优势关系满足如下性质：

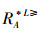
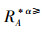
1) ，≺表示优于；

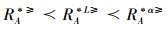
2)∀x∈U,。

定义9 设IOIS=(U,AT,V,f)是一个不完备序信息系统，∀X⊆U，A⊆AT，对象集合X在优势关系下关于属性集A⊆AT的上下近似集为：

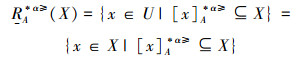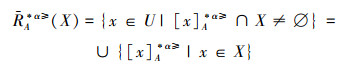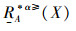
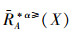
可以看出，是确定属于X的一些对象集，然而是可能属于X的一些对象集。

定理1 设IOIS=(U,AT,V,f)是一个不完备序信息系统，对于属性集∀A⊆AT，对象集∀X⊆U，则可以得出，。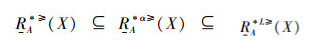

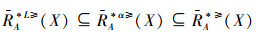
证明 由性质2可得，∀A⊆AT，∀x∈U，，结合三者关系上下近似的定义，∀X⊆U，得出，。证毕。

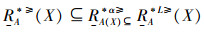
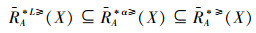
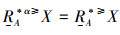
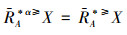
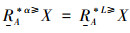
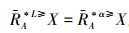
从定理1可知，当α>0时，，；当α=1时，，。从而又可以验证了基于α优势关系的粗糙集模型是文献[12]提出的优势关系粗糙集模型和文献[15]提出的限制优势关系粗糙集模型的一种扩展形式；因此，本文提出的α优势关系的粗糙集模型更具有灵活性，更加符合实际情况，更有利于去处理现实中存在的不完备序信息系统。

3 基于α优势关系粗糙集模型的属性约简 3.1 不完备序信息系统的属性约简

定义10 设IOIS=(U,AT,V,f)是一个不完备序信息系统，对于属性集A⊆AT，称属性集A是IOIS的一个优势约简当且仅当，且成立。

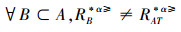
定义10表明了基于α优势关系的不完备序信息系统的属性约简保持的是对象的α优势类不变的最小属性组成的集合。基于此，下面给出其优势区分矩阵构造的方法：

定义11 设IOIS=(U,AT,V,f)是一个不完备序信息系统，对于∀x,y∈U，有

称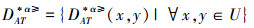为IOIS关于α优势关系的优势区分矩阵，其中属性集A为属性集AT的幂集。

根据对以往知识的了解，区分矩阵的构造是可以仅仅在单元素下进行。但是，在α优势关系的粗糙集模型中，这样的构造是不成立的，如

假设基于α优势关系的优势区分矩阵可以如下构造：

存在这样的不完备序信息系统：U={x,y}，AT={a,b,c}，x=(3,∗,2),y=(∗,2,1)，其中在属性a下，最大的取值为4；在属性b下，最大的取值为3；根据定义6和定义7，计算得出对象在条件属性集下的优势概率为：R_AT(x,y)=3/4×2/3=1/2。当α=0.6时，可以得出对象x不是对象y的α优势类，即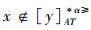；因此，运用单元素构成的优势区分矩阵对不完备序信息系统进行属性约简，可以得出其约简为空集，这显然不符合属性约简的概念。但是，当根据定义11，即运用属性集的幂集构成的优势区分矩阵对该不完备序信息系统进行属性约简时，可以得出属性集{a,b}为该系统的约简。显然，可以验证基于α优势关系粗糙集模型的优势区分矩阵应该是在属性集的幂集下进行的。

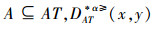
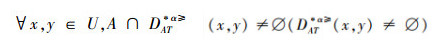
定理2 设IOIS=(U,AT,V,f)是一个不完备序信息系统，对于是基于α优势关系的优势区分矩阵，当且仅当。

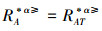
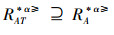
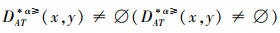
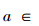
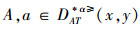
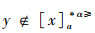
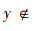
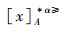
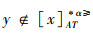
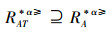
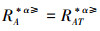
证明 (⇒)对于∀x,y∈U，A⊆AT，由性质1可得。要证明，因此只需要证明即可。然而由于 ，即存在 ，可以得出，即 ，则；因为y是任意的，所以可以得出，即。

(⇐)由于，可得∀x∈U，，则存在a∈A，当时，，即。证毕。

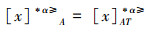
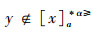
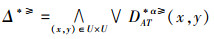
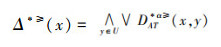
因此，令为α优势关系下不完备序信息系统的区分函数，为对象x在α优势关系下不完备序信息系统的区分函数。

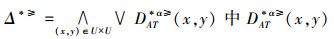
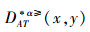
在α优势关系的不完备序信息系统中，由于区分函数是属性集的幂集组成的集合，因此，运用∧作为连接符。例如： 中区分这2个对象的属性集合为a∧b，可以写成ab。即在优势区分矩阵中，“，”表示“或”含义。

推论1 设IOIS=(U,AT,V,f)是一个不完备序信息系统，对于AT={a,b,c}，若区分函数中的2个对象可以运用属性集a、b、ab、abc加以区分，则ab、abc可以省略。

推论2 设IOIS=(U,AT,V,f)是一个不完备序信息系统，对于AT={a,b,c}，若区分函数中的2个对象仅仅能用属性集ab来区分，则属性集ab为这2个对象的区分属性集。

3.2 不完备序决策系统的属性约简

在α优势关系的不完备序信息系统中，若添加决策属性d，则不完备序信息系统可以转变为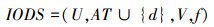情形，其中属性d也是一个准则，称之为决策属性，d∉AT且∗∉V_d，则称IODS为不完备序决策系统。

记： ，则称为决策属性d的一个优势关系。因此，可以记作： 。

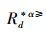
定义12 设IODS=(U,AT∪{d},V,f)是一个不完备序决策系统，若，则称α优势关系的不完备序决策系统是协调的；否则称为不协调的。

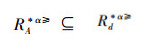
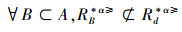
定义13 设IODS=(U,AT∪{d},V,f)是一个不完备序决策系统，对于属性集A⊆AT，称属性集A是IODS的一个优势约简当且仅当，且成立。

从定义13中可以得出，基于α优势关系的不完备序决策系统的属性约简保持α优势关系的协调性不变的最小子集。下面给出其优势决策区分矩阵构造的方法。

定义14 设IODS=(U,AT∪{d},V,f)是一个不完备序决策系统，对于∀x,y∈U，有

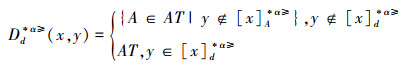其中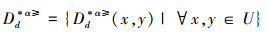称为IODS中基于α优势关系的优势决策区分矩阵。

定理3 设IODS=(U,AT∪{d},V,f)是一个不完备序决策系统，对于A⊆AT 是基于α优势关系的优势决策区分矩阵，当且仅当。

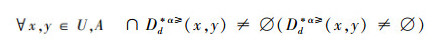
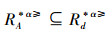
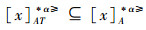
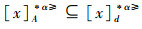
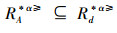
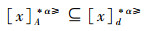
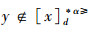
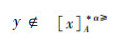
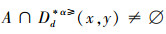
证明 (⇒)对于∀x∈U，A⊆AT，根据性质1，可以得出。又由于，即，由于对象y的任意性，则可以得出，即。

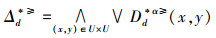
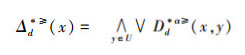
(⇐)由于，则∀x∈U，有成立。即当时，，因此。证毕。

因此，为α优势关系下不完备序决策系统的区分函数，为对象x在α优势关系下不完备序决策系统的区分函数。

4 实例分析

例1 下面给出一个不完备序决策系统，其中U={1,2,3,4,5}，AT={a,b,c}为条件属性，d为决策属性，且对象在单个条件属性a、b、c下最大的取值分别为4、3、3，最小值都是1。运用表 1给出的不完备序决策系统来分析文献[12]提出的优势关系、文献[15]提出的限制优势关系以及本文提出的α优势关系之间的性能；并计算α优势关系不完备序信息系统与决策系统的属性约简。

1)把表 1中的决策属性去掉，不完备序决策系统转化为不完备序信息系统，分析三者优势关系之间的关系。

①根据定义2，可得文献[12]提出的优势关系下，各个对象的优势类为： ，，，，。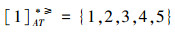

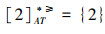
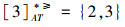
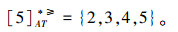
②根据定义4，可以得出文献[15]提出的限制优势关系下，各个对象的优势类为： ，，，，。

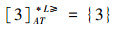
③令α=0.6，根据定义8，可得α优势关系下，各个对象的α优势类为： ，，，，。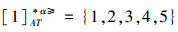

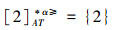
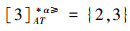
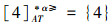
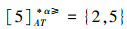
根据定义得出三者优势关系下各个对象的优势类，在文献[12]提出的优势关系下，对象4的优势类为对象2、4，然而在条件属性c下，由于对象4取得最大值，因此，对象2优于对象4的可能性是非常之小；另外，对象5的优势类为对象2、3、4、5，然而在条件属性a下，对象4优于对象5的可能性也是非常之小。因此，可以说文献[12]提出的优势关系划分的粒度过大了。在文献[15]提出的限制优势关系下，对象3的优势类为对象3，然而对象2优于对象3的可能性是非常之大。因此，说明了文献[15]提出的限制优势关系划分的粒度过细了。然而，在α优势关系下，设定确定的α取值，各个对象的优势类就不会出现上述的情况；可以看出，α优势关系吸取了上述两者优势关系的优点，丢弃了两者的缺陷，更加符合实际情况，更有利于去处理现实生活中存在复杂的不完备序信息系统。

2)不完备序信息系统的属性约简

根据定义11，结合α优势类，可以得出不完备序信息系统的优势区分矩阵如表 2。

故，即该不完备序信息系统的属性约简为abc。

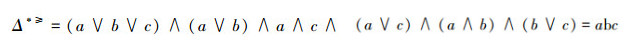
3)不完备序决策系统的属性约简。

由于各个对象在决策属性下的优势类如下：

因此，得出，即该不完备序决策系统是协调的。

根据定义14，可以得出不完备序决策系统的优势决策区分矩阵如表 3。

,即表 1中不完备序决策系统的属性约简为{a,c}或者{b,c}。

5 结束语

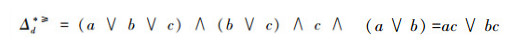
由于现实中处理的数据很多是不完备的，且存在偏序性，因此研究处理这种复杂数据情况的粗糙集方法是很有实际意义的。本文通过对现有优势关系的分析后提出了α优势关系及其相应的粗糙集模型，以使得对不完备序信息系统的数据分析更加合理。此外，在基于α优势关系的粗糙集模型上，给出了不完备序信息系统的优势区分矩阵以及不完备序决策系统的优势决策区分矩阵，从而实现了属性约简，同时也表明了区分矩阵只能运用属性集的幂集进行构造，而不能运用单个属性集进行构造。

需要指出的是，在α优势关系的基础上，还可以进一步研究不协调不完备序决策系统的属性约简算法，这是本文的下一步工作任务。