德国数学家R.Wille于1982年首先提出了形式概念分析理论[1],用于概念的发现、排序和显示。形式背景与形式概念是形式概念分析的基本概念,形式概念是由形式背景中的对象集和属性集组成的统一体,形式概念之间可形成一种有序的层次结构,即概念格,概念格的构造[2-5]是形式概念分析理论的主要研究内容之一。目前,已提出的概念格构造方法主要有2种,增量算法与批处理算法。增量算法是在数据信息不确定或不完整的情况下,当有少量数据变动时,对已经构造的概念格进行更新和维护[3,6]; 批处理算法是在数据比较完整的情况下,依据形式背景初次构造概念格的一种更有效的方法,它主要分为枚举、自顶向下和自底向上3种算法[7-8]。此外,还有将大背景横向拆分为若干小形式背景,再将各小形式背景的概念格进行横向合并,从而构建出相应的原形式背景概念格的方法[9]; 以及从对象集的每一个等价类所拥有的属性子集之间的包含关系出发,构造相应的Hasse图,从而得到概念格[10]的方法。本文对并不可约元(交不可约元)下集格中的元素定义运算,得到相应概念格的内涵集(外延集),进而扩充为概念。
1 理论基础定义1[11] 称(G,M,I)为一个形式背景,其中G={g1,g2,...,gt}为对象集,每个gi(i≤t)称为一个对象; M={m1,m2,…,ms}为属性集,每个mj(j≤s)称为一个属性; I为G和M之间的二元关系I⊆G×M。若(g,m)∈I,则称g具有属性m,用gIm表示; 否则,记为gɫm。
对于形式背景(G,M,I),在对象集X⊆G和属性集B⊆M上分别定义运算:
 |
∀g∈G,记{g}*为g*; ∀m∈M,记{m}′为m′。若∀g∈G,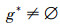
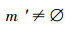
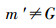
定义2[11] 设(G,M,I)是形式背景,对X⊆G,B⊆M,若满足X*=B且X=B′,则称(X,B)是一个形式概念,简称概念; 其中X称为概念的外延,B称为概念的内涵。形式背景(G,M,I)的全体概念记为L(G,M,I)。
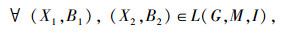 |
定义:
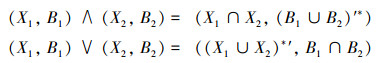 |
则L(G,M,I)是完备格,称为概念格。
定义3[11] 设(G,M,I)为形式背景,∀g∈G,m∈M,称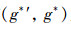
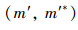
定义4[12] 设L是格,若满足下列条件,则称x∈L是并不可约元:
1)x≠0(如果L有零元);
2) 
对偶地,可得到交不可约元的定义。格L的全体并不可约元记为J(L),交不可约元记为M(L)。
定义5[12] 设P为一个偏序集,Q⊆P,如果∀x∈Q,y∈P且y≤x时有y∈Q,则称Q为下集。记P的所有下集为ο(P),称ο(P)为P的下集格。
定理1[12] 设L为有限格,L中的任意元素可表示成某些并不可约元(交不可约元)的并(交)。
定义6[11] 设(G,M,I)为形式背景,∀g∈G,
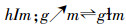


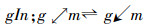
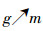
定理2[11] 下面断言对每个背景都成立:
1)对象概念
2)属性概念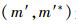
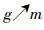
下面断言对每个有限背景都成立:
3)对象概念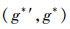
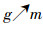
4)属性概念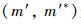
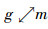
记: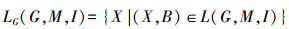
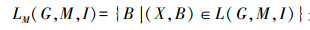
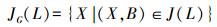
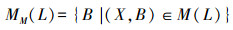
本节主要给出通过不可约元做下集格,再定义映射找到全部概念的方法。首先,根据定义6确定形式背景中的箭头关系,根据定理2找到该形式背景所对应概念格的并不可约元,其次对并不可约元的外延集做下集格,再对下集格中的元素定义映射,从而得到概念格的全部内涵集,进一步得到全部概念。利用对偶性,对交不可约元的内涵集做下集格,定义相应的映射,得到概念格的全部外延集,进而得到所有概念。
定义映射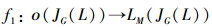
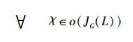
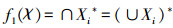

性质1 映射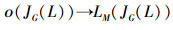
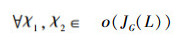

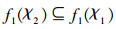
证明 1)根据f1的定义,LM(JG(L))中的元素均是由ο(JG(L))中元素的元素取并然后做*运算得到的。即∀B∈LM(JG(L)),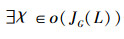
2)当χ1χ2时有
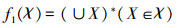
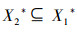
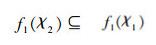
定理3 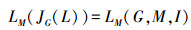
证明 一方面: ∀B∈LM(JG(L)),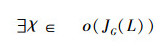
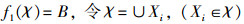
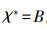

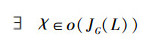


另一方面:∀A∈LM(G,M,I),设y=A′,显然有(y,A)∈ L(G,M,I)。由于概念格中的每一对概念都可以由并不可约元的并得到。从而
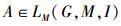
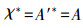
该结论表明:并不可约元外延集的下集格经f1映射后得到的集合为相应概念格的内涵集。进一步,可对所有内涵做′算子得到相应的外延,进而得到概念。对偶地,下面给出从交不可约元出发获取其下集格及所有概念的过程。
定义映射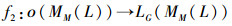
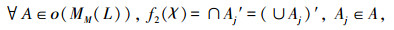
性质2 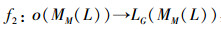

证明 1)根据f2的定义,LG(MM(L))中的元素均是由ο(MM(L))中元素的元素取并再做′运算得到的。即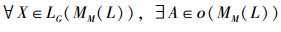
2)当A1⊆A2时有∪Ai⊆∪Aj,Ai∈A1,Aj∈A2。由于f2(A)=(∪A)′且′算子有逆序性,即对A1⊆A2,有A2′⊆A1′,从而有: f2(A2)⊆f2(A1)。
定理4 LG(MM(L))=LG(G,M,I)。
证明 一方面:∀X∈LG(MM(L)),∃A∈ο(MM(L)),使f2(A)=X。令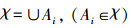
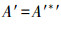

另一方面:∀Y∈LG(G,M,I),设C=Y*,显然有(Y,C)∈L(G,M,I)。由于概念格中的每一对概念都可以由交不可约元的交得到。从而∃C∈ο(MM(L)),C=∪Ci,(Ci∈C)。又由于Y∈LG(G,M,I),C′=Y*′=Y,因此Y∈LG(MM(L)),得证。
该结论表明:交不可约元属性集的下集格经f2映射后得到的集合为相应概念格的外延集。进一步,可对所有外延做*算子得到相应的内涵,进而得到概念。
例1 形式背景(G,M,I)如表 1所示,其中G={1,2,3,4,5},M={a,b,c,d,e}。
| 序号 | a | b | c | d | e |
| 1 | × | × | × | ||
| 2 | × | × | × | × | |
| 3 | × | × | × | ||
| 4 | × | × | × | ||
| 5 | × | × | × |
首先,根据定义2.6给出该形式背景的箭头关系,如表 2所示。
由表 2的箭头关系以及定理2,得到L(G,M,I)的并不可约元为(1*′,1*),(2*′,2*),(3*′,3*),(4*′,4*),(5*′,5*)。即J(L)={(1,ace),(2,abde),(23,abe),(45,bcd)}。因此,JG(L)={{1},{2},{2,3},{4,5}}。其Hasse图如图 1所示:
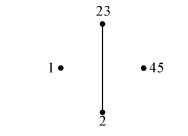
|
| 图 1 JG(L)的Hasse图 Fig. 1 Hasse of JG(L) |
根据Hasse图可得: 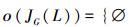
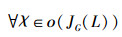
 |
由定理3可知该属性集合为L(G,M,I)的全部内涵,扩充为概念后可得: 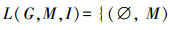
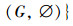
概念格如图 2所示:
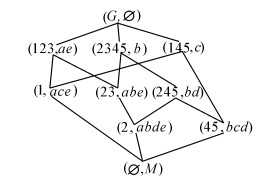
|
| 图 2 L(G,M,I) Fig. 2 L(G,M,I) |
对偶地,由表 2的箭头关系以及定理2,得到L(G,M,I)的交不可约元为(a′,a′*),(b′,b′*),(c′,c′*),(d′,d′*),(e′,e′*),即M(L)={(123,ae),(2345,b),(145,c),(245,bd)}。因此,MM(L)={{a,e},{b},{c},{b,d}}。其Hasse图如图 3所示:
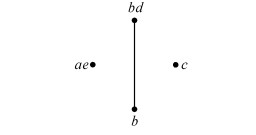
|
| 图 3 MM(L)的Hasse图 Fig. 3 MM(L) |
根据Hasse图,可得

∀A∈ο(MM(L)),计算f2(A)得到
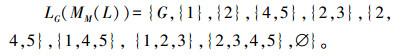 |
由定理4可知该对象集合为L(G,M,I)的全部外延。扩充为概念后可得: 
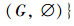
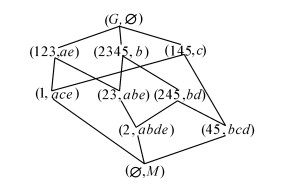
|
| 图 4 L(G,M,I) Fig. 4 L(G,M,I) |
在实际问题中,由于受到各种原因的影响,有可能导致形式背景的部分对象与属性之间出现关系缺失的现象,即这部分对象与属性之间是否存在关系无法获知,在概念格理论中,将这种含有缺失值的形式背景称为不完备形式背景。针对不完备形式背景,可以根据不完备形式背景的决策信息对缺失的信息进行预测,从而将其补全为完备的形式背景[13]; 也可以利用模糊关系的多划分技术,得到其完备化模型[14]。本节给出基于前文方法的不完备形式背景的完备化。
在本节中,不完备形式背景的缺失信息用#表达。将#全部替换为0,得到的形式背景记为(G,M,I1),相应的概念格记为L1; 将#全部替换为1,得到的形式背景记为(G,M,I2),相应的概念格记为L2。
本节借用上节概念获取的方法,对不完备形式背景的缺失信息进行补全。首先,分析形式背景(G,M,I1)与(G,M,I2),由于其概念个数不同,概念个数较多的信息系统所包含的信息要相对完整一些,因而选择从概念个数较多的形式背景出发对其完备化; 然后,找到选择出形式背景并不可约元外延集的下集格,并对其中的元素在另一个形式背景上做映射f1,得到象集后构造新集合; 最后定义映射将#映射为1或0。对偶地,找到其交不可约元的内涵集,利用相似方法对其进行完备化。
定义集合P1={A|A∈LM(JG(L1)),X∈L1M(G,M,I1)且∀m∈M,A≠m′*或A∈LM(JG(L1)),A∈L1M(G,M,I1)且∀m∈M,A≠m′*}。其中,L1M(G,M,I1)为L1的内涵集; m′*为(G,M,I2)的属性概念的内涵。
定义7映射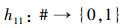
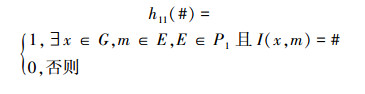 |
定义集合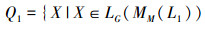


定义8 映射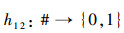
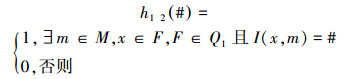 |
相应地,定义集合P2={A|A∈LM(JG(L2)),X∉L2M(G,M,I2)且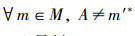
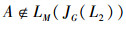


定义9 映射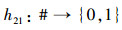
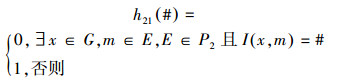 |
定义集合Q2={X|X∈LG(MM(L2)),X∉L2G(G,M,I2)且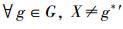
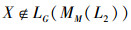
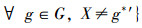
定义10 映射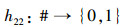
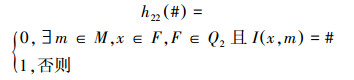 |
例2 表 3给出了一个不完备形式背景(G,M,I,#),其中G={1,2,3,4},M={a,b,c,d,e}。
| 序号 | a | b | c | d | e |
| 1 | 1 | 0 | # | 1 | 0 |
| 2 | 0 | 1 | 0 | # | 0 |
| 3 | 1 | 0 | 1 | 0 | 1 |
| 4 | 1 | 1 | 0 | 0 | 1 |
表 3中第1行的“#”符号,表示对象1是否拥有属性c是不确定的; 该表中第2行的“#”符号,表示对象2是否拥有属性d是不确定的。
下面将其完备化:
1)将不完备形式背景(G,M,I,#)中的#全部替换为0,得到形式背景(G,M,I1),如表 4所示。将不完备形式背景(G,M,I,#)中的#全部替换为1,得到形式背景(G,M,I2),如表 5所示。
| 序号 | a | b | c | d | e |
| 1 | 1 | 0 | 0 | 1 | 0 |
| 2 | 0 | 1 | 0 | 0 | 0 |
| 3 | 1 | 0 | 1 | 0 | 1 |
| 4 | 1 | 1 | 0 | 0 | 1 |
| 序号 | a | b | c | d | e |
| 1 | 1 | 0 | 1 | 1 | 0 |
| 2 | 0 | 1 | 0 | 1 | 0 |
| 3 | 1 | 0 | 1 | 0 | 1 |
| 4 | 1 | 1 | 0 | 0 | 1 |
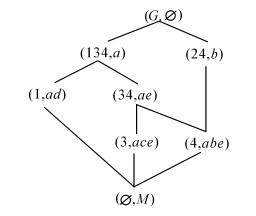
|
| 图 5 概念格L1 Fig. 5 L(G,M,I) |
|
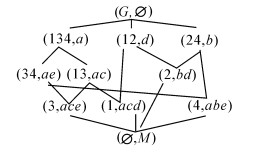
| 图 6 概念格L2 Fig. 6 L(G,M,I) |
显然,L2的概念多,所表达的信息更加完整,下面从形式背景(G,M,I2)出发,对不完备形式背景(G,M,I,#)完备化。
3)概念格L2的并不可约元如下:
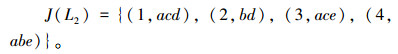 |
4)将所有并不可约元的外延构成集合:JG(L2)={{1},{2},{3},{4}}。其Hasse图如图 7所示。

|
| 图 7 JG(L2)的Hasse图 Fig. 7 Hasse of JG(L2) |
5) JG(L2)的下集格如下:

6) 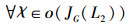
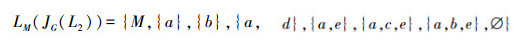
7)根据集合P2的定义,可得:P2={{d},{a,c},{b,d},{a,c,d}}
8)根据映射h21得到I(1,c)=0,I(2,d)=0。从而得到补全后的完备的形式背景(G,M,I3)如表 6所示:
| 序号 | a | b | c | d | e |
| 1 | 1 | 0 | 0 | 1 | 0 |
| 2 | 0 | 1 | 0 | 0 | 0 |
| 3 | 1 | 0 | 1 | 0 | 1 |
| 4 | 1 | 1 | 0 | 0 | 1 |
对偶地,从L2交不可约元出发对不完备形式背景完备化。
1)概念格L2的交不可约元如下:
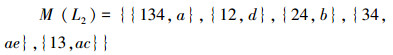 |
2)将所有交不可约元的内涵构成集合:MM(L2)={{a},{d},{b},{a,e},{a,c}}。其Hasse图如图 8所示:
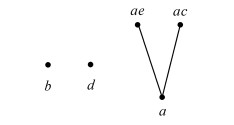
|
| 图 8 MM(L2)的Hasse图 Fig. 8 Hasse of MM(L2) |
3)MM(L2)的下集格如下:
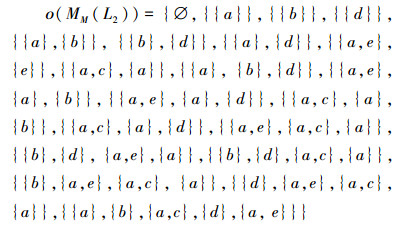 |
4)∀A∈ο(MM(L2)),在形式背景(G,M,I1)上计算f2(A)可得: 
5)根据集合Q2的定义,可得: Q2={{1,2},{1,3},{2}}
根据映射h22得到I(1,c)=0,I(2,d)=0。从而得到补全后的完备的形式背景(G,M,I4),如表 7。
| 序号 | a | b | c | d | e |
| 1 | 1 | 0 | 0 | 1 | 0 |
| 2 | 0 | 1 | 0 | 0 | 0 |
| 3 | 1 | 0 | 1 | 0 | 1 |
| 4 | 1 | 1 | 0 | 0 | 1 |
最后,以看出基于2种不可约元的下集格完备化得到的形式背景相同。因而,将其作为最终完备化的结果。
4 结束语本文提出了一种通过并不可约元(交不可约元)的下集格获取概念的方法。首先利用箭头关系找到该背景对应概念格的并不可约元(交不可约元),对并不可约元(交不可约元)的外延集(内涵集)做下集格; 其次对下集格中的元素做相应的运算,得到的属性集合(对象集合)可证明就是概念格的内涵集(外延集);最后将其扩充成为概念。此外,根据这种概念获取的方法利用下集格已经将并不可约元(交不可约元)的并(交)经行了初步筛选,所以对于不完备形式背景来说从概念较多的形式背景(G,M,I1)或(G,M,I2)的并不可约元出发,在另一个形式背景上进行特定的映射,最后根据定义的映射将其完备化。同样可以从交不可约元出发,对不完备形式背景进行扩充。并且基于2种不可约元扩充后的结果相同。
| [1] | WILLE R. Restructuring lattices theory: an approach on hierarchies of concepts[M]. Dordrecht,Holland: Springer, 1982 : 445 -470. |
| [2] | CARPINETO C,ROMANO G. Concept data analysis: theory and application[M].[S.l.]:John Wiley & Sons,2004: 21-35. |
| [3] | GODIN R. Incremental concept formation algorithm based on Galois lattices[J]. Computational Intelligence , 1995, 11 (2) : 246-267 DOI:10.1111/coin.1995.11.issue-2 |
| [4] | HO T B. Discovering and using knowledge from unsupervised data[J]. Decision Support System , 1997, 21 (1) : 29-42 DOI:10.1016/S0167-9236(97)00011-0 |
| [5] | BELOHLAVEK R. fuzzy closure operators[J]. Journal of Mathematical Analysis and Applications , 2001 (262) : 473-489 |
| [6] | NOURINE L, RAYNAUD O. A fast algorithm for building lattices[J]. Information Processing Letters , 1999, 47 : 111-112 |
| [7] | BODAT J P. Calcul pratique du treillis de galois d'ume correspondence[J]. Math Sci Hum , 1986, 96 : 31-47 |
| [8] | HO T B. Incremental conceptual clustering in the framework of galois lattice[C]//Proceedings of First Pacific-Asia Conference. Knowledge Discovery and Data Mining: Techniques and Applications. [S.l.],1997: 49-64. |
| [9] | 李云, 刘宗田, 陈崚, 等. 多概念格的横向合并算法[J]. 电子学报 , 2004, 32 (11) : 1847-1854 LI Yun, LIU Zongtian, CHEN Ling. Horizontal union algorithm of multiple concept lattices[J]. Acta Electronica Sinica , 2004, 32 (11) : 1847-1854 |
| [10] | 万青, 魏玲, 李涛. 一种基于并不可约元的建格新方法[J]. 西北大学学报 , 2013, 43 (1) : 10-14 WAN Qing, WEI Ling, LI Tao. A new method of building lattice based on join-irreducible[J]. Journal of Northwest University: Natural Science Edition , 2013, 43 (1) : 10-14 |
| [11] | GANTER B, WILLE R. Formal Concept Analysis[M]. Formal Concept Analysis New York: Mathematical Foundations.SpringerVerlag, 1999 : 21 -24. |
| [12] | DAVEY B A, PRIESTLEY H A. Introduction to lattices and order[M]. Cambridge: Cambridge University Press, 2002 . |
| [13] | 李金海.面向规则提取的概念格约简方法及其算法实现[D].西安:西安交通大学,2012: 45-63. LI Jinhai. Acquisition oriented reduction methods for concept lattices and their implementation algorithms[D].Xi'an: Xi'an Jiao Tong University,2012: 45-63. |
| [14] | 康向平, 李德玉, 李瑞萍. 基于多划分的不完备信息系统的完备化模型[J]. 计算机工程与设计 , 2011 (9) : 3131-3134 KANG Xiangping, LI Deyu, LI Ruiping. Completion model of incomplete information system based on multiple-partitions[J]. Computer Engineering and Design , 2011 (9) : 3131-3134 |








