粗糙集理论于1982年被Pawlak[1]提出以来,已经取得很大的发展。特别是在数据的决策与分析、模式识别、数据挖掘、机器学习与知识发现等方面。在粗糙集理论中有2种方式来定义近似算子:构造性方法和公理化方法。构造性方法是以论域上的二元关系、邻域系统或布尔子代数作为基本要素构造性地定义近似算子,然后得出粗糙集代数系统[2-4]。公理化方法就是先给定一个粗糙集代数系统,然后定义二元关系使得由二元关系通过构造性方法定义的近似算子及导出的粗糙集代数系统就是给定的近似算子和粗糙集代数系统[5-9]。基于这2种方法,在代数结构方面,不少学者做出了一些研究并提出了许多新的概念,如粗糙群[10]、粗糙子群[11]、粗糙不变子群[12-13]等。在线性空间方面,日本学者N. Kuroki[14]研究了线性空间上粗糙集的性质,提出了在线性空间上的等价关系以及上下近似算子。国内学者W.J.Liu [15-16]、吴明芬[17]等也研究了粗糙线性空间的性质并联系线性空间本身的性质研究更深入的性质,同时还把粗糙集引入了线性空间和模糊线性空间中。本文就是在文献[17]基础上,结合模糊逻辑及其代数分析[18]的有关概念,以及H.G.Zhang[19]对经典粗糙集上信息丢失问题的提出的方法,根据上下近似算子的性质提出了2个集合,使信息丢失的问题得到解决,并建立基于布尔代数的粗糙线性近似空间模型。
1 基本概念定义1[17] 设V是数域P上的线性空间,X、Y是V上的非空子集,k是数域P上的任意元素,定义集合的和与数乘为:
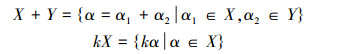 |
定义2[17] 设线性空间V上一个等价关系ρ,若对∀α,β∈V,有(α,β)∈ρ,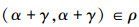
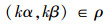

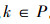
定义3[17] 设W是线性空间上V的一个子空间,定义一个二元关系ρW:
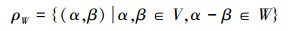 |
定理1[17] 设W是线性空间V的子空间,则下面结论成立:
1)ρW是V上的一个同余关系
2)∀α∈V,同余类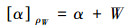
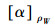
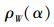
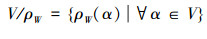
性质1[17] 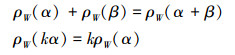
定义4[17] 设V是数域P上的线性空间,W是V的线性子空间,X是V上的任意一个非空子集,定义X在W上关于ρW的上、下近似分别为:
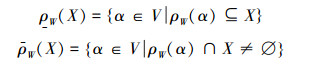 |
性质2[17] 设V是数域P上的线性空间,W是V的线性子空间,X,Y是V上的非空子集,则有:
1)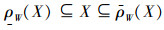
2)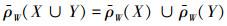
3)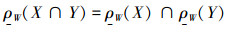
4)若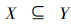
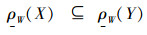
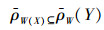
5)
6)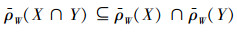
由性质2中的5)、6)可以看出,在线性空间中交的上近似、并的下近似并不是等式刻画,存在信息丢失的问题。在本节中,主要解决这一问题,为此引入以下定义:
定义5 设V是数域P上的线性空间,W是V的一个子空间,X,Y是V的2个子集,记

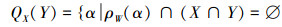
且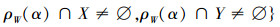
定理2:
1) 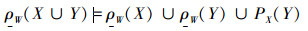
2) 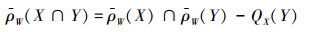
证明: 1)对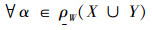
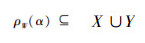
若
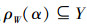
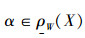
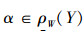
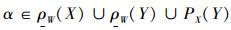
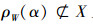
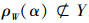
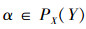
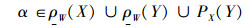
因此有
对

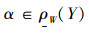
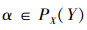
若
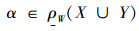
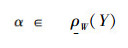

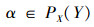
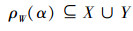
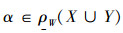
所以
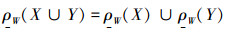
2)此命题等价为

对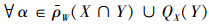
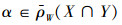
若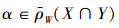
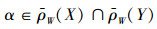
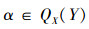

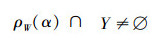
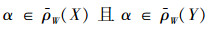
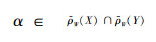
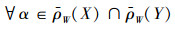

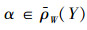

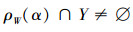
若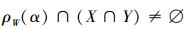
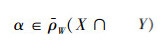
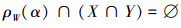
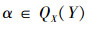
所以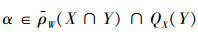
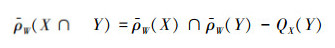
例1:设线性空间V是全体实数,定义它的加法运算为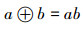
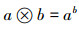
解:由定义可得
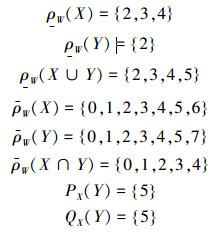 |
所以,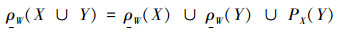

研究了基于同余关系的线性空间上下近似的性质,并通过2个集合解决了信息丢失的问题,下面要讨论上下近似的代数结构。
定义6 设V是数域P上的线性空间,X是V的任意子集,定义
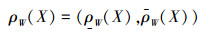 |
定义7 设V是数域P上的线性空间,X,Y是V的任意子集,则粗糙线性空间的并、交、补、差运算定义为:
1)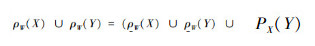
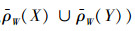
2)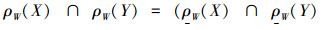
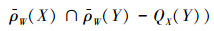
3)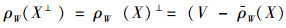
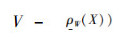
4)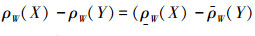

推论1 1) 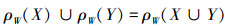
2)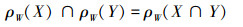
证明:由定义可得
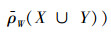
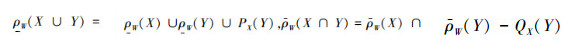
所以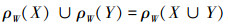
同理可得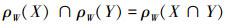
定理3 设V是数域P上的线性空间,X、Y、Z是V的任意子集,则有
1)交换律:
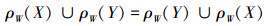
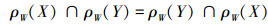
2)结合律:
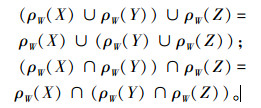 |
3)分配律:
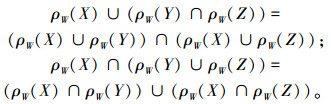 |
4)幂等律:
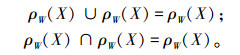 |
5)0-1律:
 |
6)互补律:
 |
7)对偶律:
 |
证明:
1)由PX(Y)和QX(Y)定义可以看出PX(Y)=PY(X),QX(Y)=QY(X)。
所以
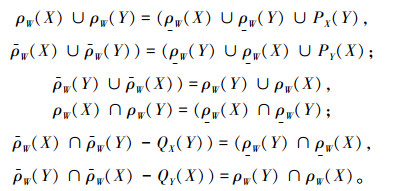 |
2)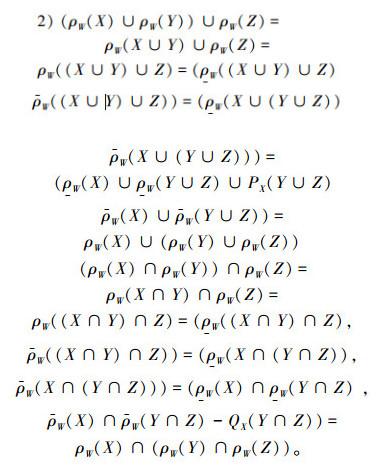
3)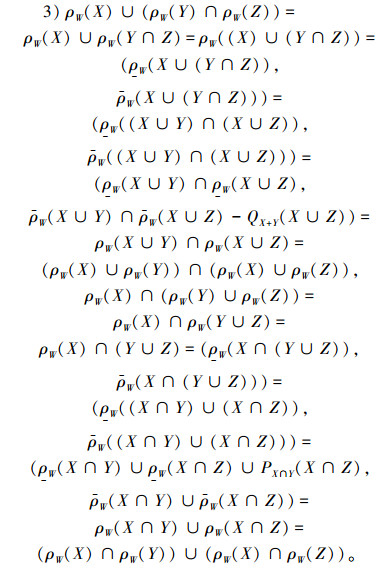
4)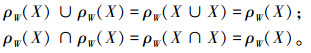
5)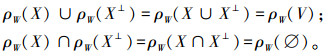
6)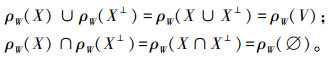
7)要证
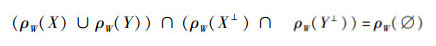
 |
所以
同理可证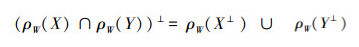
定义8: 设V是数域P上的线性空间,设(V,ρW)为粗糙线性空间,对X⊆V,定义
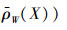
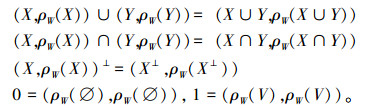 |
由以上分析可得出如下定理:
定理4 代数系统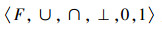
粗糙集与代数系统的结合研究是粗糙集理论研究热点之一,把粗糙集与线性空间结合研究具有重要的理论意义。在本文中,根据线性空间中集合关于同余关系的上下近似的性质,提出了2个集合以解决线性空间中信息丢失的问题,通过对上近似的交和下近似的并的等式的刻画,同时研究了粗糙线性近似空间中上下近似的代数结构并证明了其构成了布尔代数。接下来将对此代数结构进行进一步的研究。但本文缺乏实际应用,未来将对上下近似的代数结构和实际应用做进一步的研究。
| [1] | PAWLAK Z. Rough sets[J]. International Journal of Computer and Information Science , 1982, 11 : 341-356 DOI:10.1007/BF01001956 |
| [2] | WU W Z, MI J S, ZHANG W X. Generalized fuzzy rough sets[J]. Information Sciences , 2003, 151 : 263-282 DOI:10.1016/S0020-0255(02)00379-1 |
| [3] | WU W Z, ZHANG W X. Constructive and axiomatic approaches of fuzzy approximation operators[J]. Information Sciences , 2004, 159 : 233-254 DOI:10.1016/j.ins.2003.08.005 |
| [4] | 吴伟志, 张文修, 徐宗本. 粗糙模糊集的构造与公理化方法[J]. 计算机学报 , 2004, 27 (4) : 197-203 WU Zhiwei, ZHANG Wenxiu, XU Zongben. Characterizating rough fuzzy sets in constructive and axiomatic approaches[J]. Chinese Journal of Computers , 2004, 27 (4) : 197-203 |
| [5] | YAO Y Y, LIN T Y. Generalization of rough sets using modal logic[J]. Intelligent Automation and Soft Computing: An International Journal , 1996, 2 : 103-120 DOI:10.1080/10798587.1996.10750660 |
| [6] | MI J S, ZHANG W X. An axiomatic characterization of fuzzy generalization of rough sets[J]. International Journal of General Systems , 2005, 34 : 77-90 DOI:10.1080/03081070512331318329 |
| [7] | YAO Y Y. Two views of the theory of rough sets in finite universes[J]. International Journal of Approximate Reasoning , 1996, 15 : 291-317 DOI:10.1016/S0888-613X(96)00071-0 |
| [8] | YAO Y Y. Constructive and algebraic methods of the theory of rough sets[J]. Journal of Information Sciences , 1998, 109 : 21-47 DOI:10.1016/S0020-0255(98)00012-7 |
| [9] | 祝峰, 何华灿. 粗集的公理化[J]. 计算机学报 , 2000, 33 (3) : 330-333 ZHU Feng, HE Huacan. The axiomatization of the rough set[J]. Chinese Journal of Computers , 2000, 33 (3) : 330-333 |
| [10] | 韩素青. 粗糙群的同态与同构[J]. 山西大学学报:自然科学版 , 2001, 24 (4) : 303-305 HAN Suqing. Homomorphism and isomorphism of rough group[J]. Journal of Shanxi University :Natural Science Edition , 2001, 24 (4) : 303-305 |
| [11] | 张金玲, 张振良. 粗糙子群和粗糙子环[J]. 纯粹数学与应用数学 , 2004, 20 (1) : 92-96 |
| [12] | 韩素青, 胡桂荣. 粗糙陪集、粗糙不变子群[J]. 计算机科学期刊 , 2001, 28 (suppl.) : 76-77 HAN Suqing, HU Guirong. Rough coset and rough invariant subgroup[J]. Scientific Journal of Computer Science , 2001, 28 (suppl.) : 76-77 |
| [13] | 王德松, 舒兰. 粗糙不变子群的若干性质与粗糙商群[J]. 模糊系统与数学 , 2004, 18 (4) : 49-53 WANG Desong, SHU Lan. Some properties of rough invariant subgroups and rough quotient groups[J]. Fuzzy Systems and Mathematics , 2004, 18 (4) : 49-53 |
| [14] | KUROKI N. Rough sets and convex subsets in a linear space[J]. RIMS Kokyuroku , 1997, 985 : 42-47 |
| [15] | LIU W J. Rough linear space[J]. Fuzzy Systems and Mathematics , 2007, 21 : 137-143 |
| [16] | LIU W J, YANG P L. The Fuzzy Rough linear space[J]. Fuzzy Systems and Mathematics , 2006, 20 : 135-140 |
| [17] | 吴明芬. 线性空间上基于同余的上下近似[J]. 模糊系统与数学 , 2008, 22 (1) : 146-150 WU Mingfen. Upper and lower approximation based on congruences on linear spaces[J]. Fuzzy Systems and Mathematics , 2008, 22 (1) : 146-150 |
| [18] | 张小红. 模糊逻辑及其代数分析. 北京:科学出版社[M]. 2008 : 133 -134. |
| [19] | ZHANG H G, LIANG H L, LIU D R. Two new operators in rough set theory with applications to fuzzy sets[J]. Information Sciences , 2004 (166) : 147-165 |



