2. 南京理工大学 计算机科学与技术学院,江苏 南京 210094
2. School of Computer Science and Technology,Nanjing University of Science and Technology,Nanjing 210094,China
作为一种处理不精确、不确定性问题的数学工具,粗糙集理论[1] (rough set)由波兰学者Pawlak提出后便受到了广泛关注[2-4]。然而由于数据测量的误差、数据获取的限制等原因,导致了所面临的信息系统往往是不完备的。为处理这类问题,王国胤[5]提出了限制容差关系。进一步,杨习贝[6]提出了一种新的基于可变精度分类的拓展粗糙集模型,对限制容差关系进行了改进。然而,在实际工程应用中,数据的获取是需要付出一些成本或代价的,称其为测试代价。针对该问题,Min等[7-11]率先将测试代价引入到粗糙集的约简问题中,终究未能将测试代价引入到不完备信息系统环境下粗糙集本身的近似模型上。
1 基本概念形式化地,信息系统可表示为四元组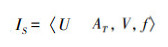
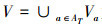
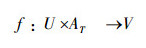
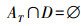
定义1[6] 设S为不完备信息系统,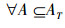
 |
(1) |
式中:PA(x)={a∈A: f(x,a)已知},α∈[0,1],| X | 表示集合X的基数,IU为恒等关系且
定义2[6] 设S为不完备信息系统,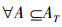
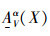
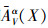
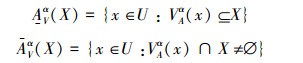 |
式中: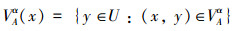
不完备信息系统环境下的粗糙集模型未考虑数据的代价问题,Min等[8]将测试代价引入到信息系统中,具体的描述见定义3。
定义3[8] 一个测试代价敏感的不完备决策系统TCSIIDS为一个五元组

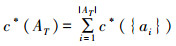

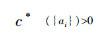

定义4 令TCSIIDS为测试代价敏感不完备决策系统,其中A⊆AT,∀x,y∈U,∀a∈A,定义特征函数如下所示:
 |
式中:Pa(x)={a∈A: f (x,a)已知}。
定义5 设TCSIIDS为测试代价敏感不完备决策系统,其中A⊆AT,由A决定的可变精度分类关系记为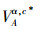
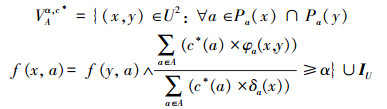 |
其中:α∈[0,1]。
定义6 设TCSIIDS为测试代价敏感不完备决策系统,A⊆AT,对于∀X⊆U,X基于可变精度分类关系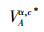
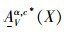
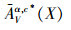
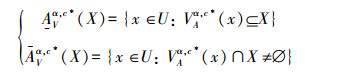 |
式中: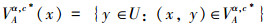
属性约简是粗糙理论的主要研究内容之一。然而,寻找决策表的最小约简已被证明是一个NP-hard问题,在处理大规模数据时计算时间代价很大,针对这一问题,许多学者提出了许多高效的约简算法,启发式搜索方法就是其中的一个典型代表。
定义7 设TCSIIDS为测试代价敏感不完备决策系统,α∈[0,1],U/IND(D)={X1,…Xn}表示根据决策属性得到的所有决策类的合集,那么U/IND(D)的近似质量可定义为
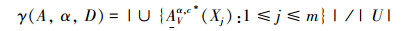 |
定理1 令TCSIIDS为测试代价敏感不完备决策系统,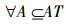
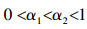
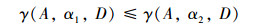 |
证明 根据定义6,定理1易证。
定义8 令TCSIIDS为测试代价敏感不完备决策系统,α∈[0, 1],A⊆AT为一个约简当且仅当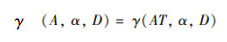
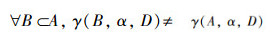
令TCSIIDS为测试代价敏感决策系统,α∈[0, 1],
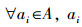
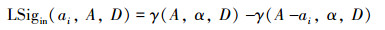 |
可以看出,LSigin(ai,B,D)反映了ai从当前条件属性集A中删除后近似质量的变化,相应地也可定义
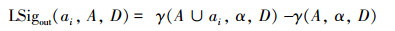 |
式中:ai∈AT-A,LSigout(ai,A,D)用以度量向属性集A增加属性ai后近似质量的变化。根据上述属性的重要度可以设计启发式属性约简算法。Min等在文献[11]中设计了传统的启发式算法(记为算法1)。其算法复杂度为
Min等从获取约简的测试代价最小出发设计出新的约简算法,即回溯算法(记为算法2)。其算法复杂度为
由上文可知回溯算法的时间复杂度为
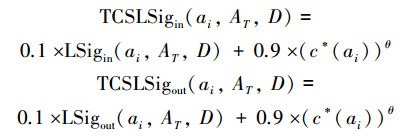 |
式中:θ≤0。可以看出,TCSLSigin(ai,AT,D)是LSigin(ai,AT,D)与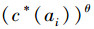
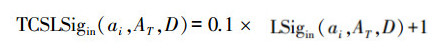
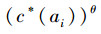
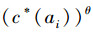
算法1 基于测试代价敏感不完备决策系统TCSIIDS综合考虑测试代价的启发式算法
输入:测试代价敏感不完备决策系统TCSIIDS,α;
输出:约简red及约简的测试代价c*(red)。
1)计算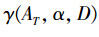
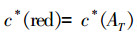
2) 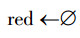
3) 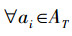
4)若
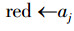
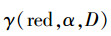
5)若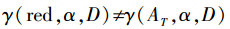
①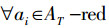
②若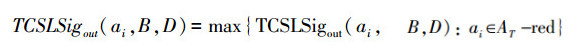
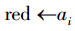
6)
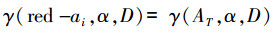
7)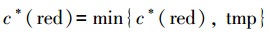
8)若θ大于给定阈值,则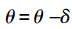
9)输出red及c*(red)。
3.2 实验分析本节将通过实验,对比算法1、算法2和算法3。表 1列出了实验中使用的4组测试数据的基本信息,所有数据集均下载于UCI数据集。由于UCI数据集中的大部分数据不含有测试代价,所以在本组实验中为每个数据集的属性随机增加了取值在[10,100]之间的测试代价。
| Data ID | Data sets | Samples | Attributes | Decision Classes |
| 1 | Bridges | 108 | 12 | 7 |
| 2 | Credit Approval | 263 | 15 | 3 |
| 3 | Heart-Disease | 303 | 14 | 5 |
| 4 | Hepatitis | 155 | 19 | 2 |
由于基于测试代价敏感的可变精度分类粗糙集模型的下、上近似集由阈值α控制,因此,在实验中选取了10组不同的α值分别对比3个算法的测试代价,在算法3的第8步中,给定阈值设为-5,步长δ为0.5,即重复求得10次约简,取其中的最小测试代价作为输出。具体的实验结果见图 1。

|
| 图 1 3种约简算法所求得的测试代价对比 Fig. 1 Comparisons among test costs obtained by three algorithms |
由图 1的实验结果,可以得到: 1)传统的启发式算法所获取的约简的测试代价最大,回溯算法所约简的测试代价最小,而综合考虑测试代价的改进的启发式算法得到约简的测试代价则是基于两者之间。2)从图 1的4个子图可以发现,3种算法的测试代价随α值的不断增加呈现先增加达到一定峰值后再下降的大致趋势,从实验的角度可看出α值在这3个算法中发挥着调节正域的作用。
4 结束语本文将测试代价引入不完备信息系统中,提出了基于测试代价敏感的可变精度分类粗糙集模型。进一步地,通过分析传统启发式约简算法未考虑测试代价以及回溯约简算法为获取最优测试需要消耗大量时间的不足,本文对传统属性重要度测量进行了改进,并根据新的属性重要度测量设计了一种新的启发式算法用以获取测试代价次优的约简。实验表明,总体而言,改进的启发式算法是寻找约简测试代价次优的合适方法。
| [1] | PAWLAK Z. Rough sets-theoretical aspects of reasoning about data[M]. Dordrecht: Kluwer Academic, 1991 . |
| [2] | HU Q H, CHE X J, ZHANG L, et al. Rank entropy based decision trees for monotonic classification[J]. IEEE Transactions on Knowledge and Data Engineering , 2012, 24 (11) : 2052-2064 DOI:10.1109/TKDE.2011.149 |
| [3] | HU Q H, PAN W W, ZHANG L, et al. Feature selection for monotonic classification[J]. IEEE Transactions on Fuzzy Systems , 2012, 20 (1) : 69-81 DOI:10.1109/TFUZZ.2011.2167235 |
| [4] | LUO G Z, YANG X B. Limited dominance-based rough set model and knowledge reductions in incomplete decision system[J]. Journal of Information Science and Engineering , 2010, 26 (6) : 2199-2211 |
| [5] | 王国胤. Rough集理论在不完备信息系统中的扩充[J]. 计算机研究与发展 , 2002, 39 (10) : 1238-1243 WANG Guoyin. Extension of rough set under incomplete information systems[J]. Journal of Computer Research and Development , 2002, 39 (10) : 1238-1243 |
| [6] | 杨习贝, 杨静宇, 於东军, 等. 不完备信息系统中的可变精度分类粗糙集模型[J]. 系统工程理论与实践 , 2008, 28 (5) : 116-121 YANG Xibei, YANG Jingyu, YU Dongjun, et al. Rough set model based on variable parameter classification in incomplete information systems[J]. System Engineering-Theory and Practice , 2008, 28 (5) : 116-121 |
| [7] | MIN F, HE H P, QIAN Y H, et al. Test-cost-sensitive attribute reduction[J]. Information Sciences , 2011, 181 (22) : 4928-4942 DOI:10.1016/j.ins.2011.07.010 |
| [8] | MIN F, LIU Q H. A hierarchical model for test-cost-sensitive decision systems[J]. Information Sciences , 2009, 179 (14) : 2442-2452 DOI:10.1016/j.ins.2009.03.007 |
| [9] | MIN F,ZHU W. Test-cost-sensitive attribute reduction based on neighborhood rough set[C]//2011 IEEE International Conference on Granular Computing. Kaohsiung,China,2011: 802-806. |
| [10] | MIN F, ZHU W. Attribute reduction of data with error ranges and test costs[J]. Information Sciences , 2012, 211 : 48-67 DOI:10.1016/j.ins.2012.04.031 |
| [11] | MIN F, HE H P, QIAN Y H, et al. Test-cost-sensitive attribute reduction[J]. Information Sciences , 2011, 181 : 4928-4942 DOI:10.1016/j.ins.2011.07.010 |



