2. 美国德州大学Dallas分校 电子工程系,Richardson 75080;
3. 北京建筑大学 电气与信息工程学院,北京 100044
2. Department of Electrical Engineering, University of Texas at Dallas, Richardson 75080, China ;
3. Department of Electrical and Information Engineering, Beijing University of Civil Engineering and Architecture, Beijing 100044, China
随着城市化进程的加速,高层和超高层建筑日益增加,人们对于建筑物安全和舒适度的要求也越来越高。在整个建筑物中,建筑电气是关键技术之一,它包括了照明系统、供配电系统、动力设备系统、办公及管理自动化等主要内容。不同子系统间的相互关联越来越紧密,同时也使建筑电气故障发生几率增加。故障智能诊断技术已在电力系统、机械等领域发展得比较成熟[1-2],但在建筑电气方面还处于空白阶段,基本依靠人工检测查找故障原因。目前关于故障诊断的算法多采用人工神经网络算法、支持向量机算法(SVM)、小波变换法等。压缩感知[3](compressive sensing,CS)方法是近年来兴起的一种新的理论算法,已在人脸识别分类和图像处理上有了广泛应用[4-6]。该理论基于线模型,其核心假设是信号的稀疏性,只要信号是稀疏或可压缩的,低维观测信号就能很好地恢复到高维原始信号。将其用于分类,也就是用训练样本本身作为基元素去表示测试样本,用与测试样本相同类的训练样本的线性组合来表示输入的待识别的样本,达到分类目的[7]。
1 建筑电气系统故障诊断原理建筑电气系统常见故障类型、表现特征及危害如表 1所示,具体故障诊断的系统结构如图 1所示。
| 故障类型 | 表现特征 | 危害 |
| 电气线路 故障 |
绝缘损坏 过负荷 断线 保护导体带电 |
短路、漏电、 引发火灾 |
| 防雷接地 系统故障 |
接地网零线带电 土壤电阻率过高 接地装置异常 |
人身遭受电击、 设备和线路遭 受损坏 |
| 设备和元 件故障 |
电动机无法启动、外 壳带电 变压器绕组绝缘 击穿 电器设备使用故障等 |
设备元件无法 正常运行,影响 生活、工作 |

|
| 图 1 建筑电气实验平台故障识别系统框图 Fig. 1 Fault identification system block diagram of the building electrical experiment platform |
建筑电气系统故障诊断实质上是基于征兆集/故障集的映射模式,即故障发生时的征兆提取和故障状态判断。由于建筑电气系统故障种类繁多且发生机率随机,所以本文以建筑电气故障模拟实验平台为研究对象,对建筑物中常见的电气故障,包括绝缘故障、接地系统故障、配电系统接地故障等进行故障诊断研究,按照不同故障工作状态的诊断目的和对象,选择便于诊断的状态信号(电流、电压及电阻值),将传感器加装于系统关键回路,通过数据采集器收集故障时异常信号,提取故障特征,输入处理后的数据,经过故障诊断算法判别输出故障类别及相应位置,提示报警信息,最后根据问题所在提出控制措施和维修策略。
2 压缩感知理论基础压缩感知理论是由Donoho与Candes等提出的理论框架,具有广阔的应用前景,受到各个领域研究人员的广泛关注。在压缩感知中,信号的稀疏表示和重构是整个理论的核心。
假设存在长度为n的信号x以及一组正交基Ψ=[ψ1 ψ2 … ψn],x可以表示为
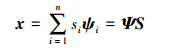 |
式中:ψi表示第i个变换基向量,Ψ=[ψ1 ψ2 … ψn]也称为稀疏矩阵;S=[s1 s2 … sn]T,S为x在稀疏矩阵Ψ上的变换系数,称为稀疏向量,S中只有k个非零值或较小值。如果在x的权重系数S中只有少量的大系数和很多的小系数,那么原始信号x就是可稀疏表示的。
在此基础上考虑信号重构问题,如果构造一个观测矩阵φ∈Rm×n(m远小于n),原始信号为x∈Rn×1,x在φ上的线性测量值为y∈Rm×1,即
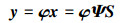 |
(1) |
式(1)展示了原始信号x在观测矩阵φ变换下的线性投影,现在考虑如何从信号y中重构出原始信号x来,理论证明,可以通过对测量值y的最优l0范数问题的求解来实现重构[8],获得x的精确或近似逼近解:
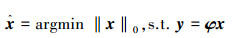 |
(2) |
但由于信号y的维数远远低于原始信号x的维数(m≪n),所以式(1)的解有无穷多个,是一个NP-hard问题,考虑到S为稀疏向量,通过合理选择观测矩阵φ和稀疏矩阵ψ,通常可将式(2)转换为求解l1范数下的最优问题:
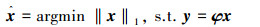 |
(3) |
求解l1优化问题,可以利用内点法、梯度投影法、二阶圆锥规划、匹配追踪法等方法求解[7]。
3 压缩感知故障诊断方法故障诊断的过程实质上就是一个分类的过程,利用故障时的异常信号,提取故障特征,通过算法判别分类各种故障类型。
3.1 训练样本的组成假设需要对k类故障进行分类,每个故障样本维数为p维,组成一个p×1维的列向量v,第i类故障的训练样本数为ni(i=1, 2, …, k),组成训练样本矩阵如式(4)所示:
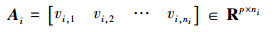 |
(4) |
式中:vi, j为第i类故障的第j个训练样本,Ai为第i类故障的训练样本矩阵。
由于样本所属类别i未知,将所有k个类别的n个训练样本拼接在一起,组成完备训练样本矩阵A:
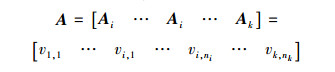 |
若待分类故障的测试样本y∈Rp属于第i类,则y可以通过第i个故障训练样本集合线性表示:
 |
式中:ai, j为权重系数。
当给定一个故障测试数据y时,该样本所属类别是未知的,需要求出它是样本集中哪种故障。因此通过完备矩阵A来线性表示出待分类的故障y:
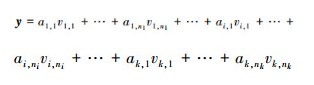 |
(5) |
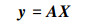 |
(6) |
利用式(5)可以解出矩阵X:
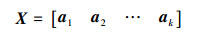 |
式中: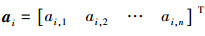
 |
因此X的系数理论上只有ai不为0,其他k-1个系数都为0,可见X是一个稀疏向量,可看作是测试样本y的稀疏分解。
3.3 测试样本分类若要求对给定的未知测试样本进行归类,那么只要根据式(6)对于每一个y解出稀疏向量X,结合已知的完备矩阵A,X上只有与该被测样本有关的ni个系数为非0值,即可知道待分类故障的类别。实际问题中通过第3节中介绍的求解l1最小化问题,获得x的精确或近似逼近解,但实际求解结果并非如理论所述,x的非零元素将会散布于很多类间,为了通过X的值完成分类工作,需采用以下分类函数[9]:
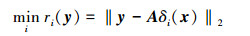 |
(7) |
式中:i=1, 2, …, k,δi(x)是指向量x中与第i类相关的行的元素。若第m个值最小(m∈[1, k]),意味着测试样本y属于第m类故障。进行故障诊断分类时,算法可按以下步骤进行:1)提取故障特征数据,构建训练样本,将每种故障类的训练样本进行顺序排列,建立完备训练样本矩阵A;2)对任一分类未知的测试样本y,进行式(4)计算,得到X;3)计算残差项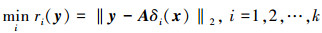
建筑电气故障模拟实验平台是本文实验室研究阶段的重要试验对象,其原产于德国,集合了住宅建筑物内部低压配电系统中常见的低压电气装置,如:断路器、熔断器、RCD(剩余电流保护器)、单向插座、三相插座等,如图 2。

|
| 图 2 建筑电气系统测试平台MA2067 Fig. 2 Experimental platform of building electrical system-MA2067 |
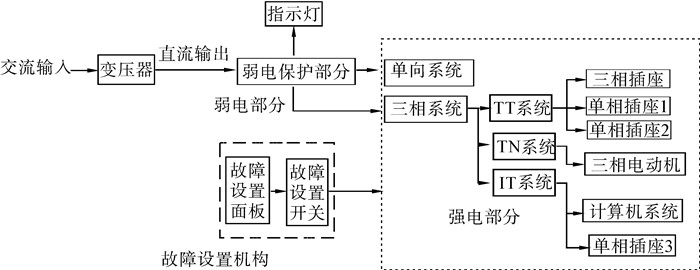
该实验平台的内部结构如图 3所示,电源供电为220 V、50 Hz交流电,由变压器转变为15V直流输出,为弱电保护板供电。弱电保护板对强电系统中的单相和三相系统进行保护。强电系统是该实验台主体,系统通过故障设置面板上的22个开关的断开闭合对强电系统中四大类阻值故障、22个故障位置进行模拟故障设置,断开即为通路,闭合即为相应部位故障发生。
|
| 图 3 建筑电气故障模拟实验平台内部结构 Fig. 3 Physical model of electrical test platform |
根据实验平台能够模拟的实际住宅建筑物中的常见故障,故障类型可分为线路阻抗故障(E1)、连续性故障(E2)、接地电阻异常(E3)、绝缘电阻过小(E4)共4种,再加上正常状态(E5),所以本文的诊断状态共有5类。通过采集实验平台10个不同测试位置的故障信息值(电阻值)作为算法输入的特征分量,位置信息如表 2所示。
| 编号 | 测试故障位置 |
| 1 | 三相插座L3相线与N相线回路 |
| 2 | 2号单相插座L1相线与N相线回路 |
| 3 | EC1-三相电机PE线线路 |
| 4 | EC1-1号灯PE线线路 |
| 5 | EC1-三相插座PE线线路 |
| 6 | 基础接地系统 |
| 7 | 防雷接地系统 |
| 8 | 3号单相插座L1相线与N相线回路 |
| 9 | 洗衣机L1相线-PE线线路 |
| 10 | 三相插座L1相线-L2相线线路 |
4.3 实验方案设计
为验证本文提出的故障诊断分类方法的有效性,设计了以下3个实验,分别采用支持向量机、基于稀疏表达分类算法的l1分类器和l2分类器。在压缩感知理论中,对于信号的重建,要求稀疏矩阵构成正交基底。利用稀疏表达(sparse representation)来做分类(见式(6)),由于完备矩阵A通常是奇异矩阵(不可逆),所以求解系数矩阵X的时候,需要采用正规化手段。本文采用了l1和l2 2种正规化方法分别来求解系数矩阵X,这2种方法的不同点在于它的目标函数[10]。
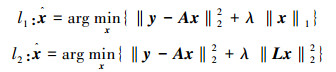 |
式中:L采用Tikhonov正则化矩阵,λ则为正则化参数。
本文通过实验平台实测收集了样本数据共55组,5种状态模式(线路阻抗故障、连续性故障、接地电阻异常、绝缘电阻过小、正常),每个样本含10个不同位置故障信息特征分量。3次实验时,每一类故障均随机选取一个样本作为测试样本,剩下的50个样本为训练样本,重复50组实验,然后取平均值作为最终分类的准确度,并计算诊断运行时间。本文实验都是运行在2.13 GHz的双核处理器上。
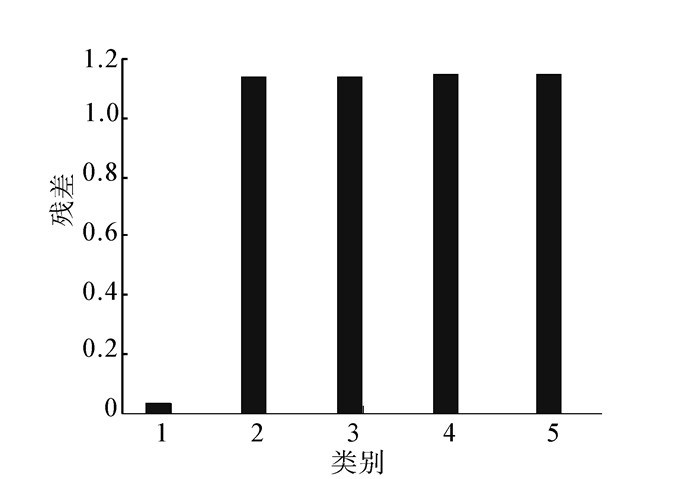
4.4 诊断结果及分析根据实验方案及步骤,此时式(6)中的矩阵A的维度为10×50,测试样本y的维度为10×1。实验结果如图 4、图 5。图 4是由l2分类器求解的x的稀疏系数(本图采用属于线路阻抗故障(E1)的测试样本),图 5即是由式(7)计算出的最终5个残差项。

|
| 图 4 稀疏表示系数x Fig. 4 The sparse representation coefficients x |
|
| 图 5 残差项ri(y) Fig. 5 The residuals ri(y) |
从图 4中可以明显看出,当输入第1类故障数据用于测试时(不在训练样本中),所得到的稀疏表示向量的确是非常稀疏的,最大系数与第1类故障训练数据相对应,则从直观上判断该测试样本应属于第1类故障。图 5则是通过数学计算方法来精确判断待测故障属于哪一类别。类别1的残差值最小,因此该测试样本属于第1类。
表 3展示了l1分类器、l2分类器以及SVM在相同实验条件和方法下的故障诊断结果。
通过表 3中数据可以看出,这3种分类算法对测试样本的识别率(准确度)都是令人满意的。但是l1分类器在运算时间上远远大于后2种方法,这在电气系统运行过程中将造成来不及使保护器动作的安全隐患,而同样是基于稀疏表示的l2分类器不论是从分类准确率和诊断时间上都优于l1分类器,可以认为本文提出的基于压缩感知理论的稀疏表示分类算法的诊断效果与支持向量机SVM算法不相上下,也可以作为建筑电气系统故障诊断的一种新方法加以推广。
5 结束语本文以建筑电气系统故障模拟实验平台数据为研究对象,提出了基于压缩感知理论的稀疏表示分类算法作为故障诊断方法引入建筑电气系统。通过实验对比,分析了l1分类器、l2分类器以及SVM在故障诊断分类中的性能。结果表明,本文提出的算法分类准确率达到了96.4%,诊断运行时间0.260 1 s,得到了较好的效果。稀疏表示分类算法不仅是对现有故障诊断方法的有益补充,也可将其进一步应用于智能型建筑电气故障诊断系统中,对于及早发现和排除故障发挥重要作用。
| [1] | 邵晓非, 宁媛, 刘耀文, 等. 电力系统故障诊断方法综述与展望[J]. 工业控制计算机 , 2012, 25 (12) : 4-7 SHAO Xiaofei, NING Yuan, LIU Yaowen, et al. Review and prospects of fault diagnosis in power system[J]. Industrial Control Computer , 2012, 25 (12) : 4-7 |
| [2] | 黄建, 胡晓光, 巩玉楠, 等. 高压断路器机械故障诊断专家系统设计[J]. 电机与控制学报 , 2011, 15 (10) : 43-49 HUANG Jian, HU Xiaoguang, GONG Yunan, et al. Machinery fault diagnosis expert system for high voltage circuit breaker[J]. Electric Machines and Control , 2011, 15 (10) : 43-49 |
| [3] | DONOHO D. Compressed sensing[J]. IEEE Transactions on Information Theory , 2006, 52 (4) : 1289-1306 DOI:10.1109/TIT.2006.871582 |
| [4] | CHEN C, TRAMEL E W, FOWLER J E. Compressed-sensing recovery of images and video using multihypothesis predictions[C]//Proceedings of the 45th Asilomar Conference on Signals, Systems, and Computers. Pacific Grove, CA, 2011: 1193-1198. |
| [5] | CHEN C, FOWLER J E. Single-image super-resolution using multihypothesis prediction[C]//Proceedings of the 46th Asilomar Conference on Signals, Systems, and Computers. Pacific Grove, CA, 2012: 608-612. |
| [6] | CHEN C, LI W, TRAMEL E W, et al. Reconstruction of hyperspectral imagery from random projections using multihypothesis prediction[J]. IEEE Transactions on Geoscience and Remote Sensing , 2014, 52 (1) : 365-374 DOI:10.1109/TGRS.2013.2240307 |
| [7] | 韩安太, 郭小华, 廖忠, 等. 基于压缩感知理论的农业害虫分类方法[J]. 农业工程学报 , 2011, 27 (6) : 203-207 HAN Antai, GUO Xiaohua, LIAO Zhong, et al. Classification of agricultural pests based on compressed sensing theory[J]. Transactions of the CSAE , 2011, 27 (6) : 203-207 |
| [8] | 蔡骋, 张明, 朱俊平. 基于压缩感知理论的杂草种子分类识别[J]. 中国科学 , 2010, 40 : 160-172 CAI Cheng, ZHANG Ming, ZHU Junping. Weed seeds classification based on compressive sensing theory[J]. Science China , 2010, 40 : 160-172 |
| [9] | WRIGHT J, YANG A, GANESH A, et al. Robust face recognition via sparse representation[J]. IEEE Trans Pattern Anal , 2009, 31 : 210-227 DOI:10.1109/TPAMI.2008.79 |
| [10] | CHEN Chen, LIU Kui, KEHTARNAVAZ N. Real-time human action recognition based on depth motion maps[J]. Journal of Real Time Image Processing , 2013 |
| [11] | 王亚慧, 张龙, 韩宁. 建筑电气系统故障诊断方法研究[J]. 计算机仿真 , 2014, 31 (2) : 436-440 WANG Yahui, ZHANG Long, HAN Ning. The research on fault diagnosis of building electrical system[J]. Computer Simulation , 2014, 31 (2) : 436-440 |



