自治水下机器人(AUV)作为海洋开发的一项重要工具,近年来取得了长足的发展。由于自治水下机器人欠驱动、强耦合、非线性等一系列特性,再加上水下作业环境比陆地上更为复杂,其轨迹跟踪控制研究仍然十分具有挑战性[1-2]。
反步控制(backstepping control)[3]是一种设计简单而又满足系统稳定的控制方法,它首先应用于地面移动机器人轨迹跟踪控制[4-5],近年来,反步方法被进一步应用到AUV的轨迹跟踪控制[6]中,通常情况下是将反步控制与其他方法集成。如L.Lionel等[7]将反步控制与Lyapunov函数结合用于AUV非线性路径跟踪控制;高剑等[8]利用级联系统理论与反步控制结合来研究欠驱动AUV水平面轨迹跟踪策略;廖煜雷等[9]将反步滑模控制应用到欠驱动水面无人艇航迹控制中,并给出了仿真计算结果。
反步控制方法原理虽然简单,但它的跟踪误差大,当期望轨迹存在拐点时,会出现速度跳变,而实现该跳需要超大数值的驱动力(力矩)支撑,在现实的AUV中显然无法或者很难实现。针对这一问题,Yang等[10-11]将反步控制方法与生物启发神经动力学模型结合,解决了地面移动机器人跟踪控制中的速度跳变问题,取得了较满意的控制效果。而在AUV反步跟踪控制方面,相关研究并不多。此外,AUV在作业时受到能源约束、海流影响、欠驱动特性等方面的限制,推进系统输出动力有限,满足跟踪时速度跳变的可能性极小,所以解决该问题的实际意义明显。
本文针对AUV反步控制过程中的速度跳变问题,同时考虑到海流因素影响,将生物启发神经动力学模型应用于AUV的水下轨迹跟踪控制中[12],通过由生物启发神经动力学模型构造的中间虚拟变量,并结合Lyapunov函数设计了AUV的轨迹跟踪控制算法。
1 海流环境下AUV的三维运动学模型实验AUV模型为上海海事大学水下机器人与智能系统实验室的“海筝二号”水下机器人,如图 1所示。

|
| 图 1 AUV推进器布置 Fig. 1 Thruster arrangements of AUV |
该AUV有4个推进器,其中水平面2个推进器对称安装于机器人尾部,控制AUV的进退(surge)和回转(yaw)运动;垂直面2个推进器对称安装于机器人重心前后,控制AUV的潜浮运动。取海面上某一固定点为惯性坐标系的原点O,OX轴和OY轴在水平面内,且互相垂直,OZ轴垂直于XOY面指向地心;取AUV的重心E为载体坐标系坐标原点,EX0轴为AUV前进方向,EY0为横移方向,EZ0为潜浮方向,如图 2所示。

|
| 图 2 AUV载体坐标系和惯性坐标系 Fig. 2 Body-fixed frame and inertial frame of AUV |
图 2中,φ、θ、ψ分别对应AUV中惯性坐标系下的横倾角、纵倾角、艏向角(以逆时针方向为正);u、v、w分别为AUV在载体坐标系中的3个速度分量;p、q、r分别为AUV在载体坐标系中的3个角速度分量。在惯性坐标系下,AUV的状态用六自由度[13]表示的向量η=[x y z φ ψ θ]T表示,x、y、z为惯性坐标系下位置,运动状态用V=[u v w p r q]T表示。
1.1 三维空间内AUV的运动学方程从图 1可以看出,AUV无侧向推进器,在三维空间中只能前后、转艏、潜浮和纵倾,不能侧移和横摇。设φ=0,p=v=0,惯性坐标系下位姿状态变为η=[x y z ψ θ]T;设AUV期望位姿为ηd=[xd yd zd yd qd]T,运动状态V=[u v w r q]T,参考速度为Vd=[ud vd wd rd qd]T。
AUV的三维运动学模型为[14]
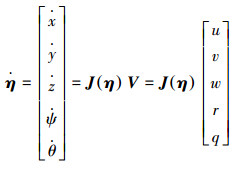 |
(1) |
式中:
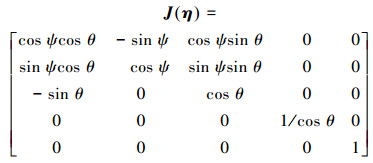 |
定义惯性坐标系下AUV的位姿误差为eη=[ex ey ez eψ eθ]T,则AUV的误差方程为
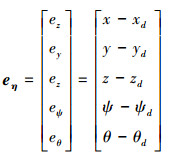 |
(2) |
对式(2)求时间导数并化简,得:
 |
(3) |
本文在反步方法的基础上,结合生物启发神经动力学模型和Lyapunov函数设计AUV的三维轨迹跟踪控制律。
1.2 海流环境下的运动学方程设惯性坐标系下海流速度为[Ux Uy Uz]T,则海流速度由惯性坐标系到载体坐标系的转换矩阵为
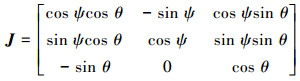 |
设海流在载体坐标系上的速度为[uc vc wc]T,则AUV相对于海流的速度为[uci vci wci]T=[u-uc v-vc w-wc]T,即[ucivciwci]T=
 |
(4) |
结合式(1)和(4)得到海流环境下AUV的运动学方程为
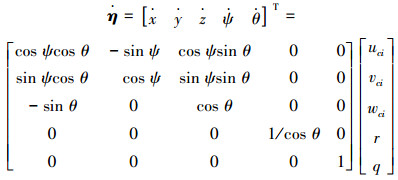 |
令[xd yd zd ψd θd]T为AUV的期望位姿矢量,即为AUV需要跟踪的参考路径。由于不考虑水动力项对AUV的影响,并且AUV没有横向推进器配置,所以当设定AUV的初始横移速度v=0时,AUV的横移速度始终保持为零。
如式(2),期望轨迹与实际AUV之间的位姿误差向量为eη=[ex ey ez eψ eθ]T,轨迹跟踪控制即设计适当的控制量,使得在一定的时间内,AUV的期望轨迹与实际AUV之间的误差能逐渐趋向于零,即[ex ey ez eψ eθ]T→0。AUV轨迹跟踪控制系统如图 3所示。AUV实际位置与期望轨迹的误差[ex ey ez eψ eθ]T,经生物启发神经动力学模型,得到虚拟的中间速度变量Vs=[Vsx Vsy Vsz Vsψ Vsθ]T,经反步控制得到轨迹跟踪的运动学控制律[u w r q]T,乘以转换矩阵J并积分,得到AUV下一时刻的位姿矢量。

|
| 图 3 系统工作图 Fig. 3 The system working drawing |
本文中的生物启发神经动力学模型的作用有:1)通过位姿与误差信号,有控制器产生虚拟离散轨迹;2)构造虚拟中间误差,即使速度有跳变,系统输出结果也能较平滑。
生物启发神经动力学模型是生物膜电压模型,整个膜电压的状态[15]可表示为
 |
式中:参数Ep、ENa、Ek分别是负漏极电流、钠离子、钾离子和在细胞膜中相应的能量,gp、gNa、gk分别是负极、钠、钾的导纳,Cm是膜电势。若令Cm=1,ζ=Ep+Vm,A=gp,B=ENa+Ep,D=Ek-Ep,S+=gNa,S-=gk。可以得生物启发方程为
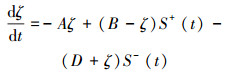 |
(5) |
式中:ζ是膜电势。A、B、D分别代表神经元活动的负衰减率、上限和下限。S+、S-对应激励与抑制输入,表示外界刺激。在AUV轨迹跟踪控制中,则代表误差大小与方向。
式(5)中,神经元活动ζ被限制,仅在[-D,B]内变化,系统稳定。存在激励输入S+(S+≥0)时,ζ增大并自动获取控制项B-ζ。如果(B-ζ)S+使ζ正向变大,当ζ超过B,(B-ζ) < 0,这时(B-ζ)S+为负,并使ζ趋于B。显然,ζ始终小于B,而抑制性输入迫使神经元活动大于-D。该模型用于轨迹跟踪则可解决速度跳变。
本文利用生物启发神经动力学模型构造的虚拟速度为
 |
(6) |
式中:ex=xd-x,ey=yd-y,ez=zd-z,eψ=ψd-ψ,eθ=θd-θ,f(ei)=max(ei,0),g(ei)=max(-ei,0),i=x,y,z,ψ,θ。
2.3 生物启发控制律设计及稳定性分析设计Lyapunov函数:
 |
(7) |
显然,当且仅当ex=ey=ez=eψ=eθ=0时,Γ=0;否则,Γ>0恒成立。对式(7)求导,有
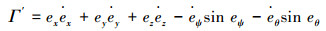 |
(8) |
将式(3)代入式(8),得
 |
(9) |
设计运动学控制律:
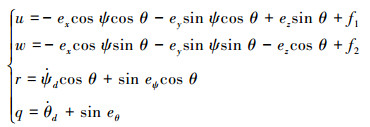 |
(10) |
式中:f1、f2为待求的未知函数。将式(10)代入式(9),得
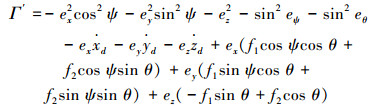 |
设
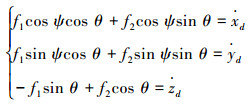 |
(11) |
由式(11)解得
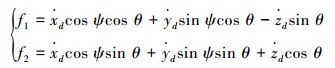 |
(12) |
将(12)式代入(11)式可得该方法下的AUV控制律为
 |
(13) |
将式(13)代入Lyapunov函数的导函数,得到Γ′=-ex2cos2ψ-ey2sin2ψ-ez2-sin2eψ-sin2eθ≤0,由Lyapunov定理可知,系统全局稳定。
将AUV相对于海流的速度[ucivciwci]T代入式(13),得海流环境下AUV的运动学控制律:
 |
应用生物启发神经动力学模型来产生与位移误差有关的辅助信号Vsx、Vsy、Vsz、Vsψ、Vsθ,如式(6)所示,并用它们代替控制律中的误差ex、ey、ez、eψ、eθ,所以得到新的控制律:
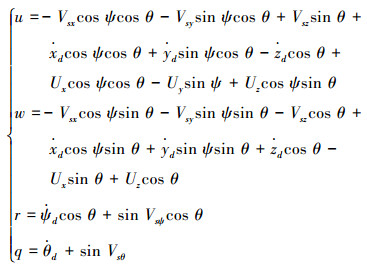 |
在MATLAB编程环境下,分别采用本文所提的控制算法和传统反步控制算法,进行AUV三维空间折线的跟踪控制,仿真结果的对比可证明本文所提控制算法的优越性。
给定三维折线期望路径的参考输入为ud=0.5,wd=0.2,rd=0,qd=0。在全局坐标下的初始位姿为xd=3,yd=0,zd=0,ψd=0,θd=0;同时AUV实际轨迹的初始位置为x=2,y=0,z=0,ψ=0,θ=0;控制参数A=1,B=1,D=2;采样时间间隔是0.01 s;海流速度[Ux Uy Uz]T=[0.2 0.2 0.1]T。该三维期望路径的起点是(3,0,0),在(6,3,3)和(9,3,3)各有一处拐点,终点是(12,6,6)。
图 4表明,在考虑了海流因素时,与传统反步控制方法相比,基于生物启发的轨迹跟踪控制器在跟踪过程中误差小,误差变化范围较小,跟踪误差能够快速趋于零,精度较高。

|
| 图 4 2种控制律的跟踪轨迹对比 Fig. 4 Comparisons between trajectories of two tracking control laws |
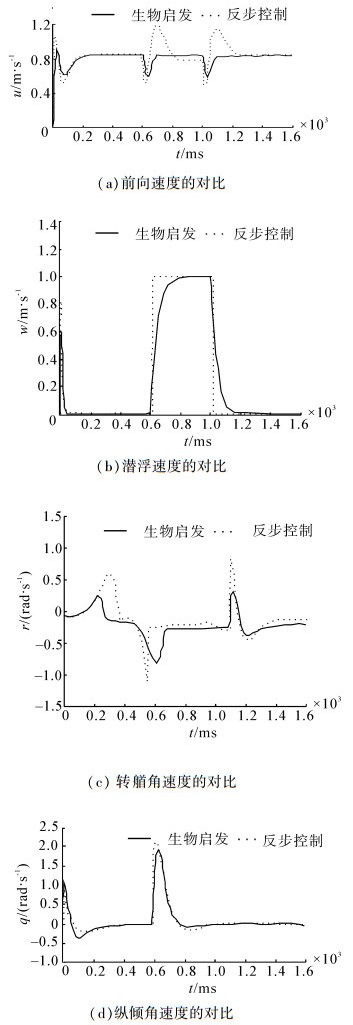
通过对图 5中凸点处的速度大小比较,可以看出加入生物启发的控制律的速度输出更加连续、平滑;生物启发轨迹跟踪控制在拐点处,速度变化明显小于传统反步跟踪控制,以图 5(a)的前向速度为例,在跟踪开始的698 s拐点处,传统反步跟踪达到1.267 m/s,而生物启发跟踪的控制速度仅为1.016 m/s,其他拐点处同样可以看出生物启发跟踪的控制速度跳变远小于传统反步跟踪控制,针对欠驱动水下机器人系统来说,短时间内较大的速度变化,意味着需要产生较大加速度,这时机器人需要提供足够的推力,但实际的水下机器人其推力有限,常常无法满足这一要求。生物启发模型的加入较好克服了控制控制的速度跳变,从而较好地实现水下机器人轨迹跟踪。
|
| 图 5 2种控制律的跟踪速度对比 Fig. 5 Tracking velocity comparison between two control laws |
通过对于三维折线轨迹进行仿真研究,分别比较了传统反步控制与生物启发方法在海流环境下的AUV跟踪控制效果,可以看到生物启发方法在跟踪效果上要优于传统反步方法,同时很好解决了反步方法的速度跳变问题,显示了很好的控制性能,同时在本文基础上可以进一步考虑将运动学控制扩展到动力学控制。
| [1] | 贾鹤鸣, 程相勤, 张利军, 等. 基于离散滑模预测的欠驱动AUV三维航迹跟踪控制[J]. 控制与决策 , 2011, 26 (10) : 1452-1458 JIA Heming, CHENG Xiangqin, ZHANG Lijun, et al. Three-dimensional path tracking control for an underactuated AUV based on discrete-time sliding mode prediction[J]. Control and Decision , 2011, 26 (10) : 1452-1458 |
| [2] | 王芳, 万磊, 李晔, 等. 欠驱动AUV的运动控制技术综述[J]. 中国造船 , 2010, 51 (2) : 227-241 WANG Fang, WAN Lei, LI Ye, et al. A survey on develop-ment of motion control for underactuated AUV[J]. Ship-building of China , 2010, 51 (2) : 227-241 |
| [3] | TSAI P S,WANG L S,CHANG F R. Systematic backstep-ping design for b-spline trajectory tracking control of the mo-bile robot in hierarchical model[C]//IEEE International Conference on Networking,Sensing and Control. Taipei,China,2004: 713-718. |
| [4] | WALLACE M B, MAX S D. EDWIN K. Depth control of re-motely operated underwater vehicles using an adaptive fuzzy sliding mode controller[J]. Robotics and Autonomous Sys-tems , 2008, 56 (8) : 670-677 DOI:10.1016/j.robot.2007.11.004 |
| [5] | BAGHERI A, MOGHADDAM J J. Simulation and tracking control based on neural-network strategy and sliding-mode control for underwater remotely operated vehicle[J]. Neuro-computing , 2009, 72 (8) : 1934-1950 |
| [6] | JON E R, ASGEIR J S, KRISTIN Y P. Model-based output feedback control of slender-body underactuated AUVs: theo-ry and experiments[J]. IEEE Transactions on Control Sys-tems Technology , 2008, 16 (5) : 930-946 DOI:10.1109/TCST.2007.916347 |
| [7] | LIONEL L, BRUNO J. Robust nonlinear path-following con-trol of AUV[J]. IEEE Journal of Oceanic Engineering , 2008, 33 (2) : 89-102 DOI:10.1109/JOE.2008.923554 |
| [8] | 高剑, 徐德民, 严卫生. 基于级联方法的欠驱动AUV全局K指数3维直线跟踪控制[J]. 控制与决策 , 2012, 27 (9) : 1281-1287 GAO Jian, XU Demin, YAN Weisheng. Global K-exponen-tial straight-line tracking control of an underactuated AUV in 3 dimensions using a cascaded approach[J]. Control and Decision , 2012, 27 (9) : 1281-1287 |
| [9] | 廖煜雷, 庞永杰, 马伟佳, 等. 喷水推进无人水面艇直线航迹系统的反步自适应滑模控制[J]. 高技术通讯 , 2013, 23 (1) : 79-84 LIAO Yulei, PANG Yongjie, MA Weijia, et al. Backstepping adaptive sliding-mode control for the straight-line trajectory system of water-jet-propelled unmanned surface vessels[J]. Chinese High Technology Letters , 2013, 23 (1) : 79-84 |
| [10] | 唐旭东, 庞永杰, 李晔, 等. 基于混沌过程神经元的水下机器人运动控制方法[J]. 控制与决策 , 2010, 25 (2) : 213-217 TANG Xudong, PANG Yongjie, LI Ye, et al. Chaotic process neuron control for AUVs[J]. Control and Deci-sion , 2010, 25 (2) : 213-217 |
| [11] | YANG S X, ZHU A. A bioinspired neurodynamics based approach to tracking control of mobile robots[J]. IEEE Transactions on Industrial Electronics , 2012, 59 (8) : 3211-3220 DOI:10.1109/TIE.2011.2130491 |
| [12] | 马岭, 崔维成. NTSM控制的AUV路径跟踪控制研究[J]. 中国造船 , 2006, 47 (4) : 77-82 MA Ling, CUI Weicheng. Path following control study of an autonomous underwater vehicle controlled by non-singu-lar terminal sliding mode[J]. Shipbuilding of China , 2006, 47 (4) : 77-82 |
| [13] | SANTHAKUMAR M, ASOKAN T. Investigations on the hybrid tracking control of an underactuated autonomous underwater robot[J]. Advanced Robotics , 2010, 24 (11) : 1529-1556 DOI:10.1163/016918610X512587 |
| [14] | 边宇枢, 高志慧, 贠超. 6自由度水下机器人动力学分析与运动控制[J]. 机械工程学报 , 2007, 43 (7) : 87-92 BIAN Yushu, GAO Zhihui, YUN Chao. Dynamic analysis and motion control of 6-DOF underwater robot[J]. Chinese Journal of Mechanical Engineering , 2007, 43 (7) : 87-92 DOI:10.3901/JME.2007.07.087 |
| [15] | SIMON X Y, LUO C. A neural network approach to com-plete coverage path planning[J]. IEEE Transactions on Systems,Man,and Cybernetics,Part B: Cybernetics , 2004, 34 (1) : 718-725 DOI:10.1109/TSMCB.2003.811769 |



