作为分布式系统的重要组成部分,时间的同步是对时间敏感的工业无线网络的关键支撑技术。时间同步[1]是解决无线传感器网络系统可靠性和稳定性难题的关键,是一个将所有节点各自不同的局部时间统一校准的过程。作为一种全新的信息获取和处理技术,无线传感器网络[2]以其功耗低、成本低、分布式和自组织的特点带来了一场信息感知的变革。其众多应用都依赖于时间同步,如TDMA调度[3]、数据融合[4]、面向波束成形的多节点协同技术[5]、基于TOF(time of flight)定位技术[6]等。因此,获取高精度的时间同步,改善同步性能,是无线传感器网络相关领域的研究热点和难点。IEEE 1588精确时间同步协议(precision time synchronization protocol,PTP) [7],在一定条件下,其时间同步的精度可控制在微秒级,且操作简单、对带宽的要求相对较低,因此在同步精度和功耗上能够较好地实现平衡,更适合应用在通信带宽及能量受限的无线传感器网络设备上[8]。
本研究在先前的工作中已将PTP协议应用于无线传感器网络,同时采用卡尔曼滤波器(Kalman filter,KF)进行优化,以提高PTP协议在无线传感器网络下的时间同步性能。工作中主要分析了在单跳环境下PTP时间同步精度与时钟戳的不确定性和延迟抖动之间的数量关系[9]。单跳仿真实验结果显示:相对于无KF优化的PTP协议,基于KF优化的PTP协议在同步精度和稳定性上均呈现明显优势。在实际网络中,从节省能源及易于部署的角度出发,一般采用多跳网络进行通信。在多跳无线传感器网络[10]中,各节点既可以是数据的终端节点,也可以成为网络的路由节点。如何将PTP协议应用于多跳无线传感器网络以提高时间同步的精度有突破性的实际意义[11]。因此本文重点研究如何在多跳无线传感器网络下实现高精度的时间同步。
本文尝试通过构建由5个节点组成的二跳同步网络,从动力学角度出发,突破传统以通信协议为研究核心的模式,通过采用状态空间模型来描述时间同步的过程,将理论分析与软件仿真相结合,进而利用均匀采样和滤波技术来抑制观测噪声,以提高时间同步的精度,并应用于无线传感器网络中,以验证基于KF优化的精确时间同步协议在多跳无线传感器网络中的拓展性和适应性。
1 多跳PTP时间同步协议模型PTP协议[7]是不同节点时钟间的同步协议,其基本原理是:子节点通过与父节点[12]交换包含时间标记信息的时间戳,计算出2级节点间的时钟偏移θ,从而估计出父节点的时间,并调整子节点的本地时钟使其与父节点的时钟保持同步。PTP协议的时间戳交换过程如图 1所示。
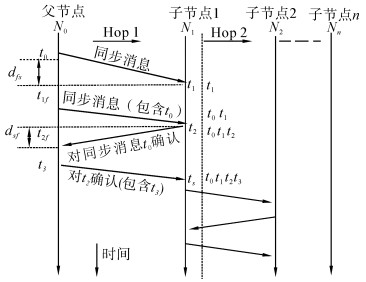
|
| 图 1 PTP协议时间戳交换过程 Fig. 1 Timing diagram of message exchange by PTP |
图 1中t0和t1为一次同步中父时钟与子时钟的时间戳;t2和t3为紧接着的下一次延迟请求报文传输的过程中,子时钟与父时钟的时间戳。考虑到两时钟间传输时延的不对等性,定义:
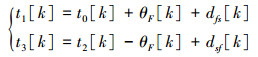 |
(1) |
式(1)描述了时间同步协议中时间戳交换过程中父子时钟标记之间的关系。其中:k代表第k次的时间同步过程,dfs代表数据包从父时钟到子时钟的传播时延,dsf代表数据包从子时钟到父时钟的传播时延。
将θ视为未知量,求解方程组(1),可得:
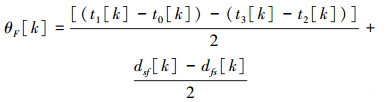 |
(2) |
式(2)描述了父子时钟的时钟偏移如何从时间戳的信息中获取的过程,是时钟偏移的观测方程。
在PTP协议中,一般假定传输时延是对等的,即dfs=dsf。但在实际中受冲突避让及无线介质共享等各种因素的影响,数据包的传输时延不对等,即dfs≠dsf。在此,用延迟抖动来描述传输时延的不对等性,把传输时延dfs和dsf看作均值为d且方差为σd2的高斯随机过程N(d, σd的2次取值。令Δd=(dsf-dfs)/2,式(2)可写为
 |
式中:Δd是均值为0且方差为σd2/2的高斯随机变量,描述了传输时延的不对等性。由于在嵌入式系统中存在着中断处理延迟等造成的时间戳的不确定性,因此在父子节点时钟的观测值ti(i=0, 1, 2, 3)中,同样存在着由于时钟值读取带来的误差Δti(i=0, 1, 2, 3)。其中Δt0和Δt3是父时钟时间戳标记的不确定性,Δt1和Δt2是子时钟时间戳标记的不确定性。由此θ的观测方程为
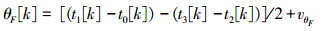 |
(3) |
式中:vθF是θ的观测噪音,定义为
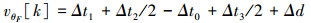 |
观测噪音vθF是传输时延不对等性Δd与时间戳标记误差Δti(i=0, 1, 2, 3)之和。假设时间戳标记的不确定性是均值为零的独立随机变量,σFTS2是Δt0和Δt3的方差,σSTS2是Δt1和Δt2的方差,那么vθF的方差是各独立随机变量的方差之和:
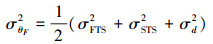 |
由于时间延迟始终是个正数,所以Δt1和Δt2的均值不为零,故vθF的均值也不为0,其值是Δt1和Δt2均值之和。假设在一个同步周期(τ[k])内vθF保持不变,则时钟偏移率α[k]可以从式(4)中计算出来,故α[k]的观测方程为
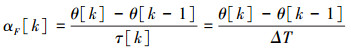 |
(4) |
同理得αF[k]的观测噪音的方差:
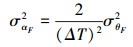 |
需要注意的是,由于αF[k]是从θ的观测值中得到的,所以观测噪音vθF与vαF耦合,其协方差为
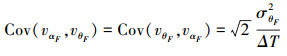 |
假设通过父子节点的同步信息包交换所获取的时间戳信息是绝对精确可靠的,则如上所述,计算所得的时钟偏移(offset)和时钟偏移率(skew)的观测值可以直接用于矫正子节点的本地时钟,以实现节点间的时间同步。实际上,由于在同步信息包交换过程中存在着很多不确定性的因素,获取得到的时间信息通常是不精确、不可靠的。因此,需要通过滤波器对其进行预处理。在已建立的同步协议模型的基础上,再加以卡尔曼滤波器方程以实现递归估计器。
由式(3)和式(4)可以得到观测方程:
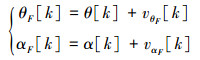 |
(5) |
将状态转移方程:
 |
和观测方程(5)写成矩阵形式,以建立时钟同步的状态空间模型:
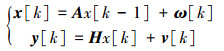 |
(6) |
式(6)分别为时钟状态方程和时钟观测方程。式中:x[k]=[θ[k]α[k]]T为第k轮的时钟状态向量;y[k]=[θF[k]αF[k]]T为第k轮的时钟观测向量;H=[1 0;0 1]为测量系统的参数矩阵方程,它将真实的状态空间映射到观测空间。A=[1 ΔT; 0 p]为状态转移矩阵。v[k]=[vθF[k]vαF[k]]T、ω[k]=[ωθ[k]ωα[k]]T分别表示观测噪声和过程噪声。v[k]和ω[k]的各样本间均相互独立,其中v[k]服从N(0, S)正态分布,ω[k]服从N(0, R)正态分布。v[k]的均值是与发送节点和接收节点相关的变量, 其均值为零的假设在实际系统中却不一定成立。然而,开展卡尔曼滤波的工作,是建立在假设v[k]均值为零的基础上的,对于由此引入的误差将反应在时间同步误差的均值上。S、R分别为观测噪音和状态噪音的协方差矩阵:
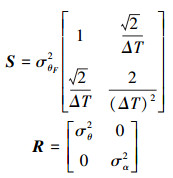 |
综上,可用公式来描述卡尔曼滤波器的迭代算法过程,式(7)、(8)为预测过程式,式(9)、(10)、(11)为更新过程:
 |
(7) |
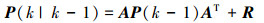 |
(8) |
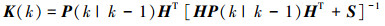 |
(9) |
 |
(10) |
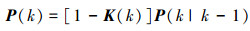 |
(11) |
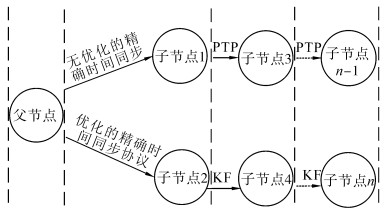
多跳同步原理如图 2所示。本实验中,为更好的模拟真实情形,构造了由5个节点组成的二跳同步网络,以验证不同协议模式下的多跳同步性能。
|
| 图 2 多跳同步拓扑结构 Fig. 2 Multi-hop synchronization topology |
在不同的观测噪声变化下,主要分析了父子时钟之间时钟偏移和时钟偏移率的估计误差平均值与标准差的变化趋势。在如下的仿真实验中,时钟模型(式(6))是用来仿真不精确时钟,其最小步长是10-6s,远小于时钟同步周期ΔΤ(ΔΤ=0.1 s),ΔΤ同时也是KF进行迭代算法的周期。观测噪声(σSTS,即子时钟做时间标记的不确定性)的变化区间为[10-8,10-4][13],反应了不同时间标记机制所引起的时延。当σSTS较小时对应了基于硬件的时间标记,此情形下的offset主要受初始θ0和频率偏移的影响;当σSTS较大时则对应于基于软件的时间标记。衡量时间同步的精确度,则是通过时钟偏移的偏移估计误差和时钟扭曲率估计误差来衡量,在实验中分别对应于估计误差的均值和估计误差的方差。
3.1 同步误差实验两跳同步误差对比仿真实验方案如表 1所示。
| 方案名称 | 同步协议名称 | 是否采用KF | 同步跳数 |
| 方案1 | PTP | 否 | 1 |
| 方案2 | PTP | 是 | 1 |
| 方案3 | PTP | 否 | 2 |
| 方案4 | PTP | 是 | 2 |
图 3、图 4反映了随观测噪声σSTS(即子节点时钟标记不确定性的标准差)的变化,时钟偏移和时钟偏移率的估计误差平均值,在4种方案下的变化趋势。
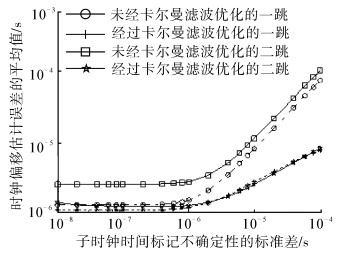
|
| 图 3 时钟偏移估计误差的平均值 Fig. 3 Means of clock offset estimation errors |
由图 3可知,随σSTS的增加,4种方案下的时钟偏移估计误差的均值变化均呈增加趋势。但基于KF优化的PTP算法的均值明显小于无KF优化的PTP算法。无KF优化的PTP算法,二跳子节点中offset的均值明显大于一跳,且同步误差的传递性较明显。基于KF优化的PTP算法,二跳子节点中offset均值与一跳相差不大,且在一跳的均值上下呈现细微摆动,故其同步误差的传递性不明显。
由图 4可知,随σSTS的增加,在无KF优化的PTP算法下子时钟偏移率估计误差的均值变化呈显著增大趋势,但在KF优化的PTP算法下,则表现出相对稳定的趋势,其值明显小于无KF优化的PTP算法。在无KF优化的PTP算法下,其二跳子节点中skew的均值大于一跳子节点的值,故同步估计误差的传递性较明显;基于KF优化的PTP算法,其二跳子节点中skew的均值略大于一跳子节点的值,故其估计误差的传递性不明显。

|
| 图 4 时钟偏移率估计误差的平均值 Fig. 4 Means of clock skew estimation errors |
图 5、图 6反应了随观测噪声(即σSTS的变化,时钟偏移和时钟偏移率同步估计误差的标准差在4种方案下的变化趋势。
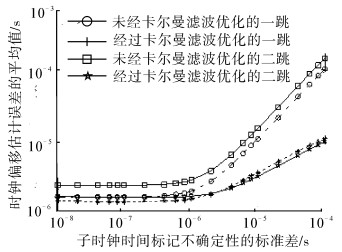
|
| 图 5 时钟偏移估计误差的标准差 Fig. 5 Standard deviation of clock offset estimation errors |
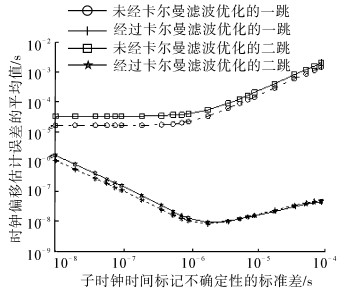
|
| 图 6 时钟偏移率估计误差的标准差 Fig. 6 Standard deviation of clock skew estimation errors |
由图 5可知,随σSTS的增加,4种方案下的时钟偏移估计误差的标准差均呈增加趋势,但基于KF优化的PTP算法的值明显小于无KF优化的PTP算法。无KF优化的PTP算法,二跳子节点中offset的标准差大于一跳,故其同步估计误差的传递性较明显。基于KF优化的PTP算法,二跳子节点中offset的标准差与一跳相差不大,故其同步估计误差的传递性不明显。
由图 6可知,随σSTS的增加,时钟偏移率估计误差标准差在无KF优化下呈明显增加趋势。但在KF优化的PTP算法下,则呈相对稳定趋势,明显小于无KF优化的PTP算法。无KF优化的PTP算法,二跳子节点中skew的标准差大于一跳同步子节点的值,且同步估计误差的传递性较明显;基于KF优化的PTP算法,二跳子节点中skew的标准差略大于对应一跳的值,故其同步估计误差的传递性不明显。
3.2 结果分析上述实验结果表明:在4种方案下,子节点的时钟偏移和时钟偏移率估计误差的均值和标准差的变化趋势反映了不同协议模式下的同步精度和稳定性的变化规律[14]。基于卡尔曼滤波器(KF)优化的PTP算法,其性能在精度和稳定性上均优于无KF优化的PTP算法,且在多跳同步中性能更优。
在多跳环境中,基于KF优化的PTP算法的时钟偏移和时钟偏移率的估计误差在精度和稳定性上具有明显优势,能表现出较好的同步性能。当观测噪声较小(即σSTS时,基于KF优化的PTP算法在单跳网络中的同步优势不明显,而在多跳网络环境中,时间同步优势明显;随观测噪声(即σSTS的逐步增大,基于KF优化的PTP算法在单跳和多跳同步中的优势均显著。由此可知,基于KF优化的PTP算法在观测噪声较大或同步跳数较多的无线传感器网络中能表现出良好的同步性能。由此说明,卡尔曼滤波器在同步过程中通过滤除同步噪声的干扰,抑制同步误差的传递,从而进一步有利于同步网络的扩展。
4 结束语通过对基于KF优化的PTP时间同步算法进行理论的分析、建模和仿真,并与单跳仿真结果对比分析可以得出如下实验结论:在多跳同步网络中,基于卡尔曼滤波器优化的精确时间同步协议,同步误差控制在微秒级、误差传递性较小且具有较好的稳定性,表现出优异的同步性能及良好的适应性并为在真实物理环境下配置无线传感器网络的相关参数提供了合理参考。
| [1] | SUNDARARAMAN B, BUY U, KSHEMKALYANI A D. Clock synchronization for wireless sensor networks: a survey[J]. Ad Hoc Networks , 2005, 3 (3) : 281-323 DOI:10.1016/j.adhoc.2005.01.002 |
| [2] | AKYILDIZ I F, SU W, SANKARASUBRAMANIAM Y, et al. Wireless sensor networks: a survey[J]. Computer Net-works , 2002, 38 (4) : 393-422 DOI:10.1016/S1389-1286(01)00302-4 |
| [3] | WEI Zhu. TDMA frame synchronization of mobile stations u-sing a radio clock signal for short range communications[C]//Proceedings of the 1994 IEEE 44th Vehicular Tech-nology Conference. 1994, 3: 1878-1882. |
| [4] | BROKMAN G, MARCH B, ROMHILD D, et al. Integrated multi-sensors for indusial humidity measurement[C]//Pro-ceedings of the IEEE International Conference on Multisen-sor Fusion and Integration for Intelligent Systems. [S.l.], 2001: 201-203. |
| [5] | MUDUMBAI R, BARRIAC G, MADHOW U. On the feasi-bility of distributed beamforming in wireless networks[J]. IEEE Transactions on Wireless Communications , 2007, 6 (5) : 1754-1763 DOI:10.1109/TWC.2007.360377 |
| [6] | CAPKUN S, CAGALJ M, SRIVASTAVA M. Secure locali-zation with hidden and mobile base stations[C]//Proceed-ings of 25th IEEE International Conference on Computer Communications. Barcelona, Spain, 2006: 1-10. |
| [7] | EIDSON J C, FISCHER M, WHITE J. IEEE 1588 standard for a precision clock synchronization protocol for networked measurement and control systems[S]// IEC 61588(E):2004—IEEE Std. 1588(E), 2002. |
| [8] | Karaki J N, Mustafa R, Kamal A E. Data aggregation and routing in Wireless Sensor Networks: Optimal and heuristic algorithms[J]. Computer Networks , 2009, 53 (7) : 945-960 DOI:10.1016/j.comnet.2008.12.001 |
| [9] | HAMITON B R, MA X, ZHAO Q, et al. Aces: adaptive clock estimation and synchronization using Kalman filtering[C]//Proc IEEE ISPCS. Ann Arbor, USA, 2008: 127-130. http://tis.hrbeu.edu.cn/oa/darticle.aspx?type=view&id=20120608 |
| [10] | 袁晓光, 杨万海, 史林. 多跳无线传感器网络决策融合[J]. 系统工程与电子技术 , 2009, 31 (4) : 976-981 YUAN Xiaoguang, YANG Wanhai, SHI Lin. Decision fu-sion in multi-hop wireless sensor networks[J]. Systems Engineering and Electronics , 2009, 31 (4) : 976-981 |
| [11] | 叶玲, 李太华, 代学武. 无线传感器网网络环境下基于卡尔曼滤波的PTP协议[J]. 智能系统学报 , 2012, 7 (6) : 518-524 YE Ling, LI Taihua, DAI Xuewu. Kalman filtering for pre-cision time synchronization in wireless sensor networks[J]. CAAI Transactions on Intelligent Systems , 2012, 7 (6) : 518-524 |
| [12] | ZENG Y, HU B, LIU S. Vector Kalman filter using multi-ple parents for time synchronization in multi-hop sensor networks[C]//Proc of the IEEE SECON. San Francisco, USA, 2008: 413-421. |
| [13] | BARENDT N, CORRELL K, BARNICKY M. Servo design considerations for software-only implementations of preci-sion time protocol[C]//ISPCS. Zurich, Switzerland, 2005: 10-12. |
| [14] | MILLS D L. Internet time synchronization: the network time protocol[M]. IEEE Computer Society Press, 1994 : 25 -36. |



