2. 宁波诺丁汉大学 计算机科学系,浙江 宁波 315100;
3. 西交利物浦大学 电气电子工程系,江苏 苏州 215123
2. Division of Computer Science, The University of Nottingham Ningbo, Ningbo 315100, China ;
3. Department of Electrical and Electronics Engineering, Xi'an Jiaotong-Liverpool University, Suzhou 215123, China
人工蜂群算法(artificial bee colony, ABC)是由土耳其学者Karaboga[2]于2005年提出,其基本思想是启发于蜂群通过个体分工和信息交流,相互协作完成采蜜任务。虽然单个蜜蜂的自身能力有限,但在没有统一指挥的情况下,整个蜂群却总是能较容易地发现优质蜜源。与经典的优化方法相比,ABC算法对目标函数和约束几乎没有要求,在搜索过程中基本不利用外部信息,仅以适应度函数作为进化的依据,形成了以“生成+检验”为特征的人工智能技术[2]。ABC算法具有操作简单、控制参数少、搜索精度较高和鲁棒性较强的特点[3-4]。文献[4]中指出与遗传算法(genetic algorithm, GA)、差分进化算法(differential evolution, DE)和粒子群优化算法(particle swarm optimization, PSO)相比较,ABC算法的求解质量相对较好。目前,ABC算法已经成功应用于人工神经网络训练、组合优化、电力系统优化、系统和工程设计等多个领域。近年来,ABC算法得到了学术界的广泛关注,但由于提出时间较晚,目前的研究成果比较分散且缺乏系统性。
1 人工蜂群算法 1.1 人工蜂群算法的生物背景蜜蜂是一种社会性群居性动物,虽然单个蜜蜂的行为简单,但群体却表现出极其复杂的智慧行为。自然界中的蜜蜂总能够高效地采集到花蜜,同时还能适应环境的改变。生物学家研究发现蜜蜂以跳舞的方式来交换蜜源信息[5]。采集到花蜜的蜜蜂,返回到蜂巢后,通过“8字舞”的形式与同伴交流蜜源信息。引领蜂跳“8字舞”的持续时间与蜜源的质量成正相关,跟随蜂根据观察到的舞蹈选择蜜源进行采蜜。引领蜂发现的蜜源质量与跟随蜂选择该蜜源的概率成正比。在一定条件下,引领蜂的角色转变为侦察蜂,在蜂巢附近随机搜索新的蜜源。蜜蜂之间的这种信息交流方式使整个蜂群能以协同的方式高效完成采集蜂蜜的工作。
蜂群实现群体智慧的最小搜索模型包括蜜源、引领蜂、跟随蜂和侦察蜂共4个组成要素,以及招募蜜蜂和放弃蜜源2种基本的行为[2, 4]。蜜蜂对蜜源的搜索一般有以下3个步骤:1)引领蜂发现蜜源并通过“8字舞”的方式共享蜜源信息;2)跟随蜂根据引领蜂所提供的蜜源信息,选择蜜源进行采蜜;3)引领蜂多次搜索找到的蜜源质量未有改善时,放弃现有的蜜源,转变成侦察蜂在蜂巢附近继续寻找新的蜜源。当搜寻到高质量的蜜源时,其角色又将转变为引领蜂。ABC算法是模拟蜜蜂的采蜜过程而提出来的群体智能算法。同遗传算法与其他的群体智能算法不同,角色转换是ABC算法特有的机制[2, 4]。蜂群通过引领蜂、跟随蜂和侦察蜂3类不同角色的转换,从而共同协作寻找高质量的蜜源[6]。在ABC算法搜索寻优的过程中,3类蜜蜂的作用有所差别:引领蜂用于维持优良解;跟随蜂用于提高收敛速度;侦察蜂用于增强摆脱局部最优的能力[6-7]。
1.2 人工蜂群算法的基本原理ABC算法在求解优化问题时,蜜源的位置被抽象成解空间中的点,代表问题的潜在解,蜜源i(i=1, 2, …, NP)的质量对应于解的适应度值fiti,NP为蜜源的数量。ABC算法将蜂群分为引领蜂、跟随蜂和侦察蜂3种类型,其中引领蜂和跟随蜂各占蜂群的一半,数量等于蜜源的数量,且每个蜜源同一时间内只有一只引领蜂采蜜[2, 4]。
设求解问题的维数为D,在t次迭代时蜜源i的位置表示为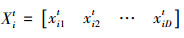
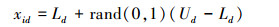 |
(1) |
在搜索开始阶段,引领蜂在蜜源i的周围根据式(2)搜索产生一个新的蜜源:
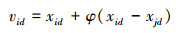 |
(2) |
式中:d是在[1, D]中的一个随机整数,表示引领蜂随机地选择一维进行搜索;j∈{1, 2, …, NP},j≠i, 表示在NP个蜜源中随机选择一个不等于i的蜜源;φ是[-1, 1]均匀分布的随机数,决定扰动幅度(magnitude of the perturbation)。当新蜜源Vi=[vi1 vi2…vid]的适应度优于Xi时,采用贪婪选择的方法用Vi代替Xi,否则保留Xi。所有的引领蜂完成式(2)的运算后,飞回信息交流区共享蜜源信息。跟随蜂根据引领蜂分享的蜜源信息,按式(3)计算的概率进行跟随:
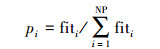 |
(3) |
然后,跟随蜂采用轮盘赌的方法选择引领蜂,即在[0,1]>产生一个均匀分布的随机数r,如果pi大于r,该跟随蜂按式(2)在蜜源i的周围产生一个新蜜源,且采用同引领蜂相同的贪婪选择的方法确定保留的蜜源。
搜索过程中,如果蜜源Xi经过trial次迭代搜索到达阈值limit而没有找到更好的蜜源,该蜜源Xi将会被放弃,与之对应的引领蜂角色转变为侦察蜂。侦察蜂将在搜索空间随机产生一个新的蜜源代替Xi,上述过程如式(4):
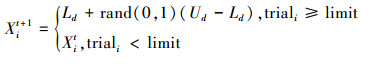 |
(4) |
为不失一般性,以最小化的优化问题为例,在ABC算法中,解的适应度评价依据式(5)计算。
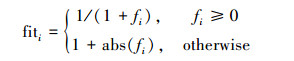 |
(5) |
式中:fi表示解的函数值。
综上所述,ABC算法的核心包括3个部分:1)引领蜂搜索蜜源;2)引领蜂分享蜜源信息,跟随蜂以一定的概率选择蜜源进行搜索;3)侦察蜂在搜索空间随机搜索。
1.3 人工蜂群算法的步骤1)初始化各蜜源Xi;设定参数NP、limit以及最大迭代次数;t=1;
2)为蜜源Xi分配一只引领蜂,按式(2)进行搜索,产生新蜜源Vi;
3)依据式(5)评价Vi的适应度,根据贪婪选择的方法确定保留的蜜源;
4)由式(3)计算引领蜂找到的蜜源被跟随的概率;
5)跟随峰采用与引领蜂相同的方式进行搜索,根据贪婪选择的方法确定保留的蜜源;
6)判断蜜源Xi是否满足被放弃的条件。如满足,对应的引领蜂角色变为侦察蜂,否则直接转到8);
7)侦察蜂根据式(4)随机产生新蜜源;
8)t=t+1;判断算法是否满足终止条件,若满足则终止,输出最优解,否则转到2)。
2 人工蜂群算法的改进基本的ABC算法主要存在以下问题:1)ABC算法存在“早熟”的收敛性缺陷[8];2)ABC算法具有较好的探索能力,但开发能力不足,局部搜索能力较弱,收敛速度相对较慢[9-10]。针对ABC算法的不足,国内外的学者提出了较多的改进方法,研究成果简单归纳为算法参数调整、混合算法和设计新的学习策略3个方面。
2.1 算法的参数调整Akay和Karaboga[11]通过多组实验系统研究了参数设置对ABC算法性能的影响,实验结果表明:1) ABC算法对问题维数不太敏感,适合于求解高维问题;2)群体规模(colony size,CZ)对ABC算法的性能影响不明显,即使较小的群体规模仍可获得满意解;3) limit值对算法的性能有较大的影响,太小的limit不利于蜂群协作搜索,太大的limit降低了算法的探索能力,对于较复杂的函数,limit设置为(CZ∗D)是较好的初始选择。为了使初始解具有多样性,较均匀地分布在搜索空间,暴励等[12]采用反向学习(opposition-based learning)的方法产生初始解。罗钧等[13]利用混沌序列初始化的方法,提高了解的多样性和遍历性。Akay和Karaboga[6]在基本ABC算法的基础上增加了修改率(modification rate, MR)的参数,其用于控制搜索的扰动维数,给出了基于Rechenberg 1/5变异规则的自适应调整扰动幅度的方法。在基本ABC算法中,跟随蜂按照式(3)计算选择蜜源的概率,这种方法容易导致较大的选择压力(selection pressure),群体多样性难以维护。Bao等[14]对ABC算法的选择机制进行系统分析和比较,并提出了3种新的选择机制:裂变选择(disruptive selection)、排序选择(rank selection)和竞标赛选择(tournament selection), 实验结果表明了新的选择机制的有效性。Konrady等[15]研究了基于跟随蜂与引领蜂之间距离的选择方法,当跟随蜂与引领蜂的距离越小时,跟随蜂选择该引领蜂发现蜜源的概率越大,反之选择概率越小。Lee等[16]在ABC算法中引入群体多样性的机制,根据群体多样性的门槛值选择采用不同的搜索公式。Rajasekhar等[17]利用Levy分布具有正态分布与柯西分布的特点,给出了基于Levy分布变异的改进ABC算法。Alam等[18]提出了一种基于指数分布的自适应变异步长机制的ABC算法,动态控制搜索过程中的探索和开发能力。Alatas[19]在基本ABC算法中运用混沌映射机制实现参数的适应变化,提高了算法收敛速度和全局搜索能力。
2.2 混合算法根据“没有免费午餐定理”,没有任何单一的智能算法可以包揽所有的优点,它们自身都会存在一定的缺陷。不同的智能优化算法具有某些相同的机制和原理,但它们表现出不同的行为特征。例如,GA强调群体的进化能力,ABC算法强调群体之间的协作,PSO算法强调群体的学习。因此,在众多的智能优化算法中,相互之间的融合便成为自然。目前一些学者提出了混合其他智能优化算法算子的改进ABC算法,研究集中在ABC算法与DE算法、PSO算法和细菌觅食优化(bacterial foraging optimization,BFO)算法的混合。黄玲玲等[20]分析了DE算法和ABC算法的各自特点,提出了一种集成二者优势的混合算法。在DE算法的启发下,Gao和Liu[21]提出了2种改进蜜源搜索公式的ABC算法。Stanarevic[22]将DE算法的变异算子嵌入ABC算法中,并比较了不同变异算子对ABC算法性能的影响。Chen等[23]在引领峰的搜索过程中加入了模拟退火算子,提高了ABC算法的开发能力。Duan等[24]提出了一种融合ABC算法和量子进化的混合算法用于求解连续优化问题,该混合算法中利用量子进化提高了跳出局部最优的能力。考虑基本的ABC算法没有利用全局最优的引导信息,Mustafa[25]设计了基于ABC和PSO的混合算法,该算法将ABC搜索的全局最优位置与PSO搜索的全局最优位置进行重组作为PSO新的全局最优和ABC算法跟随蜂的邻居。El-Abd[26]提出了一种运用ABC算法改善PSO算法中粒子个体最优位置的混合算法。Shi等[27]提出了一种基于PSO和ABC的混合算法,该算法提出了2种信息交换机制从而实现PSO和ABC的信息共享和交流,提高了全局搜索能力。Zhong等[28]将BFO算法中的趋化行为嵌入到ABC算法中,提高了局部搜索性能。
还有相当部分的学者将数学、物理和生物等学科的一些技术嵌入到ABC算法中。Kang等[29]将Nelder-Mead单纯形技术融入到ABC算法中,成功用于实际的工程优化问题。文献[30]提出了一种混合Rosenbrock旋转和ABC算法的改进优化方法,二者共同协调完成有效搜索,其中探索主要通过ABC算法实现,而开发主要依赖于Rosenbrock旋转。Kang等[31]提出混合Hooke-Jeeves模式搜索的改进ABC算法,其基本思想同文献[30]类似,算法的探索和开发分布依靠ABC算法和模式搜索实现。文献[32]将混沌优化与ABC算法相结合,利用混沌变量的随机性、遍历性和规律性,提高了算法的局部搜索能力和跳出局部最优的能力。毕晓君等[33]利用小生境技术维持种群的多样性,采用自由搜索(free search)算法中的信息素-灵敏度模型代替跟随蜂进行蜜源选择的轮盘赌方法,提出了一种求解多峰函数的混合ABC算法。
2.3 设计新的学习策略从蜜源搜索式(2)可以看出基本ABC算法的搜索主要是通过个体与个体之间的交互学习来实现的,这种学习策略具有较好的探索能力,但是开发能力较差,影响了ABC算法的收敛速度和搜索精度[10]。因此,设计新的学习策略平衡探索与开发能力是提高ABC算法性能的一条重要途径。
Banharnsakun等[10]在跟随蜂的搜索公式上添加了迄今为止最佳个体(Best-so-far)的适应度值来提高开发能力,且搜索半径随着迭代次数增加呈线性递减,标准测试函数的实验结果和在图像压缩上的应用表明该算法能快速搜索到高质量的解。Li等[8]在基本ABC算法的蜜源搜索公式上添加了惯性权重和加速系数、惯性权重和加速系数根据适应度值确定。在DE算法的启发下,Gao和Liu[34]提出了2种改进的蜜源搜索公式:“ABC/best/1”和“ABC/rand/1”。类似于PSO算法,Zhu等在蜜源搜索公式上增加了全局最优位置的引导,并对增加的参数进行了实验分析,结果表明改进算法能较好地平衡探索和开发能力。Tsai等[35]将引领蜂与跟随蜂之间的关系利用万有引力定律进行描述,提出了一种交互作用的ABC算法。Liu等[36]分析了基本ABC算法在搜索时没有考虑配对个体之间的适应度好坏,可能误导搜索方式,从而提出了一种基于相互学习(mutual learning)的改进ABC算法。为提高搜索能力,Gao等[37]提出一种改进的蜜源搜索公式,将解的每一维看成是一次抽样,通过正交学习策略可以产生更具前景的解,提出了基于改进的搜索公式和正交学习的ABC算法。
目前,对ABC算法的改进研究都在一定程度上提高了性能,但表现各有优劣。通过目前文献的研究结果和研究态势来看,“设计新的学习策略”将是一种最具前景的改进方法,但是这方面的研究还不成熟和深入,研究成果相对较少。
3 人工蜂群算法的约束优化约束优化问题是科学和工程应用领域中广泛存在但较难求解的问题。目前,求解约束优化问题主要可以分为经典优化方法和智能优化算法。经典优化方法需要梯度信息,对初值敏感,且所求得的解多为局部最优。智能优化算法具有鲁棒性强、搜索效率高,且能以较大概率搜索到全局最优解的特点,比较而言,更加适合于求解约束优化问题。
Deb规则是处理约束优化问题的一种常见方法,在ABC算法中得到较多应用。Deb规则采用了竞标赛选择的方法区别对待不可行解和可行解[38],简单描述为:1)可行解总是优于不可行解;2)在可行解中,按适应度值的大小排序;3)在2个不可行解中,违背约束量较小的不可行解优先选择。Karaboga和Basturk[39]最早提出了基于Deb规则求解约束优化问题的ABC算法。比较有代表性的工作是Karaboga和Akay在2011年发表的文章[40],其不但运用Deb规则处理约束,而且根据可行解的适应度值和不可行解违背约束的程度计算随蜂选择蜜源的概率。Tuba等[41]采用同文献[40]的方法处理约束,区别在于侦察蜂不是在搜索空间随机寻找蜜源,而是在最优蜜源和另一个蜜源的共同引导下搜寻。Li等[42]提出了一种自适应的ABC算法求解约束优化问题,引领蜂搜索阶段采用了Deb规则,跟随蜂搜索阶段将约束优化问题转化为多目标问题,给出了MR的自适应机制。采用Deb规则处理优化问题简单易行,但其存在一定的缺陷[43]:1)难于维持群体的多样性;2)当最优解位于或靠近边界的时候,Deb规则的效果不佳。
罚函数是处理约束优化问题常用的方法,通过对目标函数增加惩罚项,转化为无约束问题。罚函数方法的难点在于设置合理的惩罚因子,太小的惩罚因子可能导致解的不可行,反之太大的惩罚因子容易陷入局部最优。Sonmez[43]提出了自适应惩罚因子的方法来处理约束,惩罚因子的大小在迭代过程中根据群体的进化信息自适应变化,在构架结构设计的优化中体现了优异的性能。
还有部分学者根据ABC算法的特点,提出了一些相应处理约束优化问题的方法。Mezura-Montes等[44]提出了一种处理约束优化问题的精英ABC算法,针对约束优化问题,该算法分别给出了新的引领蜂、跟随蜂和侦察蜂的蜜源搜索公式,加入了动态容忍量的方法处理等式约束,针对全局最优位置采用了局部搜索。Mezura-Montes等[45]同时提出了采用了智能飞行算子和ε约束的ABC算法。Stanarevic等[46]提出了求解约束优化问题的改进ABC算法,该算法采用了“智慧蜂”记忆蜜源的位置和质量。
4 人工蜂群算法的多目标优化科学实践、工程系统设计及社会生产和经济发展中的许多优化问题都是多目标优化问题。多目标优化问题的特点是不存在惟一的全局最优解,求解多目标优化问题的实质是要寻找解的集合。传统的多目标优化方法一般要求对问题本身有较多的先验认识。与传统的多目标优化方法相比,智能优化算法求解多目标优化问题更具优势,主要体现在:1)智能优化算法在一次运行中可以获得多个Pareto最优解;2)智能优化算法容易处理具有非连续的或非凸的Pareto前沿问题,应用范围广。
目前,多目标ABC算法的研究相对较少。Omkar等[47]提出了类似于VEGA(vector evaluation genetic algorithm,VEGA)的VEABC算法,与VEGA具有类似的缺陷,VEABC的结果容易走向某些极端边界解,且对Pareto最优前端的非凸部分敏感。Zou等[48]提出了基于外部档案(archive)方法和广泛学习策略的一种用于解决多目标优化问题的ABC算法,其中外部档案用于保存获得的非支配解,广泛学习的策略用于保证解的多样性。Akbari等[49]提出一种较新的多目标ABC算法,该算法采用基于网格的方法自适应评估Pareto前沿,外部档案用于保存非支配解和控制蜜蜂的飞行行为,引领蜂根据外部档案的非支配解调整飞行轨迹,跟随蜂依据引领蜂找到的食物质量更新个体位置,侦察蜂用于删除质量较差的蜜源,标准测试函数的实验结果表明它是一种非常具有竞争力的多目标ABC算法。Zhang等[50]根据自然生态系统中的物种共生现象,提出了基于多蜂巢的多目标ABC算法,采用了NSGA-Ⅱ的快速支配排序方法和拥挤距离的概念,并且提出了蜂巢之间的信息传递策略和高质量个体的分离算子(division operator)。Li等[51]设计了求解柔性车间调度的离散多目标ABC算法,采用交叉算子,充分利用引领蜂的有价值信息,外部档案用于存储非支配解,给出了一种快速更新外部档案的方法。此外,Akay[52]研究了同步更新和异步更新方法对多目标ABC算法性能的影响。
5 人工蜂群算法的应用研究ABC算法是为求解函数优化问题而提出来的,较多的研究集中于此。ABC算法求解函数优化问题具有天然的优势,也是目前应用最为成功的领域。经过学者们的研究,将ABC算法的应用领域不断推广,目前已经成功应用于神经网络训练、组合优化、电脑系统优化、系统和工程设计等多个领域。
5.1 神经网络训练Karaboga等[53]最早应用ABC算法于训练前馈神经网络。Ozurk等[54]提出了ABC算法和Levenberg-Marquardt的混合方法用于训练神经网络。Zhang等[55]基于适应度缩放和混沌理论提出一种改进的ABC算法,并应用于前馈神经网络的训练。Kurban等[56]采用ABC算法训练RBF神经网络,并与GA、卡尔曼滤波和梯度下降算法进行了比较,结果表明ABC算法是一种高效训练RBF的算法。Yeh等[57]于2011年提出了应用ABC算法和蒙特卡洛模拟训练递归神经网络,并成功应用于预测网络的可靠性。Garro等[58]采用ABC算法同时优化神经网络的结构、连接权重和转换函数。
5.2 组合优化经典的优化方法一般难以求解组合优化问题。目前,ABC算法在旅行商问题、生产调度、项目调度、车辆路径问题和背包问题等组合优化问题中都有成功应用。针对旅行商问题的特点,Karaboga和Gorkemli[59]设计了求解旅行商问题的ABC算法。ABC算法在生产调度领域得到较多应用,涉及到置换流水线调度[60]、阻塞流水线调度[61]、基本车间调度[62]、柔性车间调度[63]、批量流水线调度[64]、混合流水线调度[65]和订单调度[66-67]等。Shi等[68]采用随机键的编码机制,利用ABC算法求解资源受限情况下的项目调度问题。孙晓雅等[69]研究了求解任务中可定点拆分的资源受限项目调度问题的ABC算法。ABC算法在容量约束的车辆路径问题的应用也得到学者们的一定关注[70]。Sundar等[71]将启发式的修补算子和局部搜索方法融入到ABC算法中,采用了适当的编码用来求解多维背包问题。Singh[72]利用ABC算法在一个给出的无向带权图中成功找出具有叶子约束的最小生成树。
5.3 电力系统优化Cobanli等[73]运用ABC算法求解电力系统中有功率损耗最小化的问题。Özyön等[74]通过目标加权的方式将环境经济调度问题转变为一个单目标问题,利用ABC算法进行求解。Rezaei Adaryani等[75]在考虑燃料成本、有功功率损耗和电压稳定性等因素的情况下,构建了非线性非凸的多目标的最优潮流模型,运用ABC算法对模型进行求解。Hemamalini等[76]采用ABC算法求解成本函数为非光滑的负荷经济批量调度问题。Ayan和Kilic[77]应用了ABC算法求解最优无功潮流(optimal reactive power flow)的优化问题,对IEEE 30-bus和IEEE 118-bus的求解结果表明了ABC算法的有效性。Govardhan[78]等采用了ABC算法求解机组最优启停(optimal unit commitment)问题,并将求解结果与PSO算法、DE算法进行了比较。
5.4 系统与工程设计许多工程与系统设计问题在本质上都是函数优化的问题,ABC算法非常适合这类问题的求解。目前,ABC算法在越来越多的工程与系统设计优化问题中取得了成功应用。这些问题包括:机械设计[79]、结构模式的识别[80]和复合材料分层成分设计[47]等。除此之外,ABC算法在可靠性冗余分配[81]、数据挖掘[82]、股市价格预测[83]和图像分析[84]等诸多领域也得到了广泛应用。
6 结论与展望ABC算法以其良好的搜索性能和简单易操作的性能,受到了学术界的广泛关注。综观ABC算法的研究现状,总体来说,其相关的研究仍处于初级阶段,有很多问题值得进一步的研究,简单归纳如下:
1)ABC算法的理论研究。
同其他智能优化算法相似,ABC算法的理论研究匮乏,从理论上无法剖析算法的行为。鉴于算法收敛模型的建立和收敛性的分析是算法研究和改进的基础,该方面的工作具有一定的挑战性。
2)ABC算法参数的自适应策略。
参数的合理设置对于算法的性能具有非常重要的影响。通常意义上来说,参数的设置具有问题依赖性。因此,根据问题的特征和搜索进程,设计参数自适应变化的机制对于提高算法的性能具有重要意义。一些学者提出了DE、GA和PSO等算法的参数自适应方法,但ABC算法该方面的研究比较匮乏。
3)多目标ABC算法的研究。
多目标智能优化算法是当前一个热门的研究领域。与其他多目标智能优化算法相比,目前多目标ABC算法的研究成果偏少,且不够系统。ABC算法在求解单目标问题上已经体现出优异的性能,如何设计高效的多目标ABC算法将是一个值得深入研究的课题。
4)设计更加符合真实自然的ABC算法。
ABC算法受蜜蜂觅食行为的启发而提出,模拟了蜜蜂觅食的部分行为。真实自然环境中蜜蜂的觅食行为更为复杂,例如:蜂群采蜜时进行了合理分工,但在某些特殊情况下,蜜蜂的职能可以发生转化,如他们的年龄变化、性激素、由遗传决定的个体的倾向等。综合考虑这些因素,将蜜蜂觅食的一些特性通过抽象设计合适的算子嵌入到ABC算法中,将进一步推动ABC算法的发展。
5)ABC算法的动态优化研究。
现实世界的问题往往随时间变化的,近年来,将智能优化算法应用于动态环境中已经成为一个热门的研究领域。根据发表的研究文献来看,还鲜见ABC算法相关的研究成果。
| [1] | KENNEDY J, EBERHART R C, SHI Y. Swarm intelligence[M]. San Francisco: Morgan Kaufmann Publishers, 2001 : 1 -35. |
| [2] | KARABOGA D. An idea based on honey bee swarm for numerical optimization[R]. Computers Engineering Department, Engineering Faculty, Erciyes University, 2005. |
| [3] | KARABOGA D, AKAY B. A comparative study of artificial bee colony algorithm[J]. Applied Mathematics and Computation , 2009, 2 (14) : 108-132 |
| [4] | KARABOGA D, BASTURK B. On the performance of artificial bee colony (ABC) algorithm[J]. Applied Soft Computing , 2008, 8 (1) : 687-697 DOI:10.1016/j.asoc.2007.05.007 |
| [5] | TERESHKO V, LOENGAROV A. Collective decision-making in honeybee foraging dynamics[J]. Computing and Information Systems Journal , 2005, 9 (3) : 1-7 |
| [6] | KARABOGA D, BASTURK B. A powerful and efficient algorithm for numerical function optimization: artificial bee colony (ABC) algorithm[J]. Journal of Global Optimization , 2007, 39 : 459-471 DOI:10.1007/s10898-007-9149-x |
| [7] | AKAY B, KARABOGA D. A modified artificial bee colony algorithm for real-parameter optimization[J]. Information Sciences , 2012, 192 : 120-142 DOI:10.1016/j.ins.2010.07.015 |
| [8] | LI G Q, NIU P F, XIAO X J. Development and investigation of efficient artificial bee colony algorithm for numerical optimization[J]. Applied Soft Computing , 2012, 12 : 320-332 DOI:10.1016/j.asoc.2011.08.040 |
| [9] | ZHU G, KWONG S. Gbest-guided artificial bee colony algorithm for numerical function optimization[J]. Applied Mathematics and Computation , 2010, 217 (7) : 3166-3173 DOI:10.1016/j.amc.2010.08.049 |
| [10] | BANHARNSAKUN A, ACHALAKUL T, SIRINAOVAKUL B. The best-so-far selection in artificial bee colony algorithm[J]. Applied Soft Computing , 2011, 11 (2) : 2888-2901 DOI:10.1016/j.asoc.2010.11.025 |
| [11] | AKAY B, KARABOGA D. Parameter tuning for the artificial bee colony algorithm[C]//Lecture Notes in Computer Science. Berlin, Germany, 2009, 5796: 608-619. |
| [12] | 暴励, 曾建潮. 一种双种群差分蜂群算法[J]. 控制理论与应用 , 2011, 28 (2) : 266-272 BAO LI, ZENG Jianchao. A bi-group differential artificial bee colony algorithm[J]. Control Theory and Applications , 2011, 28 (2) : 266-272 |
| [13] | 罗钧, 李研. 具有混沌搜索策略的蜂群优化算法[J]. 控制与决策 , 2010, 25 (12) : 1913-1916 LUO JUN, LI YAN. Artificial bee colony algorithm with chaotic-search strategy[J]. Control and Decision , 2010, 25 (12) : 1913-1916 |
| [14] | BAO L, ZENG J C. Comparison and analysis of the selection mechanism in the artificial bee colony algorithm [C]// The 2009 9th International Conference on Hybrid Intelligent Systems. Shenyang, China, 2011: 411-416. |
| [15] | KONRAD D, ANDREJ A, ALEXANDER S, et al. Performance evaluation of artificial bee colony optimization and new selection schemes[J]. Memetic Computing , 2011, 3 : 149-162 DOI:10.1007/s12293-011-0065-8 |
| [16] | LEE W P, CAI W T. A novel artificial bee colony algorithm with diversity strategy[C]//The 7th International Conference on Natural Computation. Shanghai, 2011: 1441-1444. |
| [17] | RAJASEKHAR A, ABRAHAM A, PANT M. Levy mutated artificial bee colony algorithm for global optimization[C] //IEEE International Conference on Systems, Man and Cybernetics. Anchorage, USA, 2011: 665-662. |
| [18] | ALAM M S, UI KABIR M W, ISLAM MM. Self-adaption of mutation step size in artificial bee colony algorithm for continuous function optimization[C]//The 2010 13th International Conference on Computer and Information Technology. Dhaka, Bangladesh, 2010: 69-74. |
| [19] | ALATAS B. Chaotic bee colony algorithms for global numerical optimization[J]. Expert Systems with Applications , 2010, 37 (8) : 5682-5687 DOI:10.1016/j.eswa.2010.02.042 |
| [20] | 黄玲玲, 刘三阳, 高卫峰. 具有人工蜂群搜索策略的差分进化算法[J]. 控制与决策 , 2012, 27 (11) : 1644-1648 HUANG Lingling, LIU Sanyang, GAO Weifeng. Differential evolution with the search strategy of artificial bee colony algorithm[J]. Control and Decision , 2012, 27 (11) : 1644-1648 |
| [21] | GAO W F, LIU S Y. Improved artificial bee colony algorithm for global optimization[J]. Information Process Letters , 2011, 111 (17) : 871-882 DOI:10.1016/j.ipl.2011.06.002 |
| [22] | STANAREVIC N. Comparison of different mutation strategies applied to artificial bee colony algorithm[C]//The 5th European Computing Conference. Paris, Frence, 2011: 257-262. |
| [23] | CHEN S M, SAROSH A, DONG Y F. Simulated annealing based artificial bee colony algorithm for global numerical optimization[J]. Applied Mathematics and Computations , 2012, 219 : 3575-3589 DOI:10.1016/j.amc.2012.09.052 |
| [24] | DUAN H B, XU C F, XING Z H. A hybrid artificial bee colony optimization and quantum evolutionary algorithm for continuous optimization problems[J]. International Journal of Neural Systems , 2010, 20 (1) : 39-50 DOI:10.1142/S012906571000222X |
| [25] | MUSTAFA S K, MESUT G. A recombination-based hybridization of particle swarm optimization and artificial bee colony algorithm for continuous optimization problems[J]. Applied Soft Computing , 2013, 4 (13) : 2188-2203 |
| [26] | EL-ABD M. A hybrid ABC-SPSO algorithm for continuous function optimization[C]//IEEE Symposium on Swarm Intelligence. Paris, Frence, 2011: 1-6. |
| [27] | SHI X, LI Y, LI H, GUAN R, et al. An integrated algorithm based on artificial bee colony and particle swarm optimization[C]//The 2010 6th International Conference on Natural Computation. Yantai, China, 2010, 5: 2586-2590. |
| [28] | ZHONG Y, LIN J, NING J, et al. Hybrid artificial bee colony algorithm with chemotaxis behavior of bacterial foraging optimization algorithm[C]//The 2011 7th international conference on natural computation. [S.l.], 2011, 2: 171-1174. |
| [29] | KANG F, LI J J, XU Q. Structural inverse analysis by hybrid simplex artificial bee colony algorithms[J]. Computers and Structures , 2009, 87 (13/14) : 861-870 |
| [30] | KANG F, LI J J, MA Z. Rosenbrock artificial bee colony algorithm for accurate global optimization of numerical functions[J]. Information Sciences , 2011, 181 (16) : 3508-3531 DOI:10.1016/j.ins.2011.04.024 |
| [31] | KANG F, LI J J, LI H J. Artificial bee colony algorithm and pattern search hybridized for global optimization[J]. Applied Soft Computing , 2013, 13 (4) : 1781-1791 DOI:10.1016/j.asoc.2012.12.025 |
| [32] | HONG W C. Electric load forecasting by seasonal recurrent SVR(support vector regression) with chaotic artificial bee colony algorithm[J]. Energy , 2011, 36 (9) : 5568-5578 DOI:10.1016/j.energy.2011.07.015 |
| [33] | 毕晓君, 王艳娇. 用于多峰函数优化的小生境人工蜂群算法[J]. 系统工程与电子技术 , 2011, 33 (11) : 2564-2568 BI Xiaojun, WANG Yanjiao. Niche artificial bee colony algorithm for multi-peak function optimization[J]. Systems Engineering and Electronics , 2011, 33 (11) : 2564-2568 |
| [34] | GAO W F, LIU S Y. A modified artificial bee colony algorithm[J]. Computers and Operations Research , 2012, 39 (3) : 687-697 DOI:10.1016/j.cor.2011.06.007 |
| [35] | TSAI P W, PAN J S, LIAO B Y, et al. Enhanced artificial bee colony optimization[J]. Information and Control , 2009, 5 (12) : 1-12 |
| [36] | LIU Y, LING X X, LIANG Y, et al. Improved artificial bee colony algorithm with mutual learning[J]. Journal of Systems Engineering and Electronics , 2012, 23 (2) : 265-275 DOI:10.1109/JSEE.2012.00034 |
| [37] | GAO W F, LIU S Y, HUANG L L. A novel artificial bee colony algorithm based on modified search equation and orthogonal learning[J]. IEEE Transaction on Systems, Man and Cybernetics , 2013, 43 (3) : 1011-1024 |
| [38] | DEB K. An efficient constraint handling method for genetic algorithms[J]. Computer Methods in Applied Mechanics and Engineering , 2000, 186 (2/3/4) : 311-338 |
| [39] | KARABOGA D, BASTURK B. Artificial bee colony (ABC) optimization algorithm for solving constrained optimization problems[C]//Lecture Notes in Artificial Intelligence. Berlin, Germany, 2007: 789-798. |
| [40] | KARABOGA D, AKAY B. A modified artificial bee colony (ABC) algorithm for constrained optimization problems[J]. Applied Soft Computing , 2011, 11 : 3021-3031 DOI:10.1016/j.asoc.2010.12.001 |
| [41] | TUBA M, BACANIN B, STANAREVIC N. Guided artificial bee colony algorithm[C]//The 5th European Computing Conference. Paris, Frence, 2011: 398-403. |
| [42] | |
| [43] | SONMEZ M. Artificial bee colony algorithm for optimization of truss structures[J]. Applied Soft Computing , 2011 : 2406-2418 |
| [44] | MEZURA-MONTES E, VELEZ-KOEPPEL R E. Elitist artificial bee colony for constrained real-parameter optimization [C]//The 2010 IEEE Congress on Evolutionary Computation. Barcelona, USA, 2010: 1-8. |
| [45] | MEZURA-MONTES E, DAMIAN-ARAOZ M, CETINA-DOMINGEZ O. Smart flight and dynamic tolerances in artificial bee colony for constrained optimization[C]//The 2010 IEEE Congress on Evolutionary Computation. Barcelona, USA, 2010: 4118-4125. |
| [46] | STANAREVIC N, TUBA M, BACANIN B. Modified artificial bee colony algorithm for constrained problems optimization[J]. International Journal of Mathematical Models and Methods in Applied Science , 2011, 5 (3) : 644-651 |
| [47] | OMKAR SN, SENTHILNATH J. Artificial bee colony (ABC) for multi-objective design optimization of composite structures[J]. Applied Soft Computing , 2011, 11 (1) : 489-499 DOI:10.1016/j.asoc.2009.12.008 |
| [48] | ZOU W, ZHU Y L, CHEN H N, et al. Solving multi-objective optimization problems using artificial bee colony algorithm[J]. Discrete Dynamics in Nature and Society , 2011, 6 (2) : 182-197 |
| [49] | AKBARI R, HEDAYATZADEH R, ZIARATI K, et al. A multi-objective artificial bee colony algorithm[J]. Swarm and Evolutionary Computation , 2012 (2) : 39-52 |
| [50] | ZHANG H, ZHU Y L, YAN X H. Multi-hive artificial bee colony algorithm for constrained multi-objective optimization[C]//The 2012 IEEE Congress on Evolutionary Computation. Brisbane, Australia, 2012: 1-8. |
| [51] | LI J Q, PAN Q K, GAO K Z. Pareto-based discrete artificial bee colony algorithm for multi-objective flexible job shop scheduling problems[J]. International Journal of Advanced Manufacturing Technology , 2011, 55 : 1159-1169 DOI:10.1007/s00170-010-3140-2 |
| [52] | AKAY B. Synchronous and asynchronous Pareto-based multi-objective artificial bee colony algorithms[J]. Journal of Global Optimization , 2013, 57 (2) : 415-445 DOI:10.1007/s10898-012-9993-1 |
| [53] | KARABOGA D, AKAY B. Artificial bee colony (ABC) algorithm on training artificial neural networks[C]//The IEEE 15th Signal Processing and Communications Applications Conference. Eskişehir, Turkey, 2007(1/2/3): 818-821. |
| [54] | OZTURK C, KARABOGA D. Hybrid artificial bee colony algorithm for neural network training[C]//The 2011 IEEE Congress on Evolutionary Computation. New Orleans, USA, 2011: 84-88. |
| [55] | ZHANG Y, WU L, WANG S. Magnetic resonance brain image classification by an improved artificial bee colony algorithm[J]. Progress in Electromagnetics Research , 2011, 116 : 65-79 DOI:10.2528/PIER11031709 |
| [56] | KURBAN T, BEDOK E. A comparison of RBF neural network training algorithms for inertial sensor based terrain classification[J]. Sensors , 2009 (9) : 6312-6329 |
| [57] | YEH W C, SU J C P, HSIEH T J, et al. Approximate reliability function based on wavelet Latin hypercube sampling and bee recurrent neural network[J]. IEEE Transaction on Reliability , 2011, 60 (2) : 404-414 DOI:10.1109/TR.2011.2134190 |
| [58] | GARRO B A, SOSSA H, VAZQUEZ R A. Artificial neural network synthesis by means of artificial bee colony (ABC) algorithm[C]//The 2011 IEEE Congress on Evolutionary Computation. New Orleans, 2011: 331-338. |
| [59] | KARABOGA D, GORKEMLI B. A combinatorial artificial bee colony algorithm for traveling salesman problem[C]// International Symposium on Innovations in Intelligent Systems and Applications. Istanbul, Turkey, 2011: 50-53. |
| [60] | TASGETIREN M F, PAN Q K, SUGANTHAN P N, et al. A discrete artificial bee colony algorithm for the total flowtime minimization in permutation flow shops[J]. Information Sciences , 2011, 181 : 3459-3475 DOI:10.1016/j.ins.2011.04.018 |
| [61] | HAN Y Y, PAN Q K, LI J Q, et al. An improved artificial bee colony algorithm for the blocking flowshop scheduling problem[J]. International Journal of Advanced Manufacturing Technology , 2012, 60 : 149-1159 DOI:10.1007/s00170-011-3599-5 |
| [62] | ZHANG R, SONG S J, WU C. A hybrid artificial bee colony algorithm for the job shop scheduling problem[J]. International Journal of Production Economics , 2013, 141 : 167-178 DOI:10.1016/j.ijpe.2012.03.035 |
| [63] | WANG L, ZHOU G, XU Y. An effective artificial bee colony algorithm for the flexible job-shop scheduling problem[J]. International Journal of Advanced Manufacturing Technology , 2012, 60 : 1111-1123 DOI:10.1007/s00170-011-3665-z |
| [64] | PAN Q K. A discrete artificial bee colony algorithm for the lot-streaming flow shop scheduling problem[J]. Information Science , 2011, 18 (12) : 2455-2468 |
| [65] | 王凌, 周刚, 许烨, 等. 求解不相关平行机混合流水线调度问题的人工蜂群算法[J]. 控制理论与应用 , 2012, 29 (12) : 1551-1557 WANG LING, ZHOU GANG, XU YE, et al. An artificial bee colony algorithm for solving hybrid flow-shop scheduling problem with unrelated parallel machines[J]. Control Theory and Applications , 2012, 29 (12) : 1551-1557 |
| [66] | WANG X L, XIE X Z, CHENG T C E. A modified artificial bee colony algorithm for order acceptance in two-machine flow shops[J]. International Journal of Production Economics , 2013, 141 : 14-23 DOI:10.1016/j.ijpe.2012.06.003 |
| [67] | LIN S W, YING K C. Increasing the total net revenue for single machine order acceptance and scheduling problems using an artificial bee colony algorithm[J]. Journal of Operational Research Society , 2013, 64 : 293-311 DOI:10.1057/jors.2012.47 |
| [68] | SHI Y J, QU F Z, CHEN W, et al. An artificial bee colony with random key for resource-constrained project scheduling[C]//Lecture Notes in Computer Science. Berlin, Germany, 2010: 148-157. |
| [69] | 孙晓雅, 林焰. 任务可定点拆分的资源受限项目调度问题研究[J]. 微电子学与计算机 , 2011, 28 (11) : 53-56 SUN Xiaoya, LIN Yan. A study on resource-constrained project scheduling with splitable at fixed point[J]. Microelectronics and Computer , 2011, 28 (11) : 53-56 |
| [70] | SZETO W Y, WU Y Z, HO S C. An artificial bee colony algorithm for the capacitated vehicle routing problem[J]. European Journal of Operational Research , 2011, 215 (1) : 126-135 DOI:10.1016/j.ejor.2011.06.006 |
| [71] | SUNDAR S, SINGH A, ROSSI A. An artificial bee colony algorithm for the 0-1 multidimensional knapsack problem[J]. Communications in Computer and Information Science , 2010, 94 (1) : 41-151 |
| [72] | SINGH A. An artificial bee colony algorithm for the leaf-constrained minimum spanning tree problem[J]. Applied Soft Computing , 2009, 9 (2) : 625-631 DOI:10.1016/j.asoc.2008.09.001 |
| [73] | COBANLI S, OZTURK A, GUVENC U, et al. Active power loss minimization in electric power systems through artificial bee colony algorithm[J]. International Review of Electrical Engineering , 2010 (5) : 2217-2223 |
| [74] | ÖZYÖN S, YASAR C, ÖZCAN G, et al. An artificial bee colony algorithm (ABC) approach to environmental economic power dispatch problems[C]//The 2011 National Electrical-electronics and Computer Symposium. [S.l.], Turkey, 2011: 222-228. |
| [75] | REZAEI A M, KARAMI A. Artificial bee colony algorithm for solving multi-objective optimal power problem[J]. International Journal of Electrical Power and Energy Systems , 2013, 53 : 219-230 DOI:10.1016/j.ijepes.2013.04.021 |
| [76] | HEMAMALINI S, SIMON S P. Artificial bee colony algorithm for economic load dispatch problem with non-smooth cost functions[J]. Electric Power Components and Systems , 2010, 38 (7) : 786-803 DOI:10.1080/15325000903489710 |
| [77] | AYAN K, KILIC U. Artificial bee colony algorithm for optimal reactive power flow[J]. Applied Soft Computing , 2012, 12 (5) : 1477-1482 DOI:10.1016/j.asoc.2012.01.006 |
| [78] | GOVARDHAN M, ROY R. Gbest based artificial bee colony optimization for unit commitment problem[C]// International Conference on Energy Efficient Technologies for Sustainability. Kanyakumari, India, 2013: 1138-1143. |
| [79] | AKAY B, KARABOGA D. Artificial bee colony algorithm for large-scale problems and engineering design optimization[J]. Journal of Intelligent Manufacturing , 2010, 23 (4) : 1001-1014 |
| [80] | SUN H, LUS H, BETTI R. Identification of structural models using a modified artificial bee colony algorithm[J]. Computers and Structures , 2013, 116 : 59-74 DOI:10.1016/j.compstruc.2012.10.017 |
| [81] | YEH W C, HSIEH T J. Solving reliability redundancy allocation problems using an artificial bee colony algorithm[J]. Computers and Operations Research , 2011, 38 (11) : 1465-1473 DOI:10.1016/j.cor.2010.10.028 |
| [82] | KARABOGA D, OZTURK C. A novel clustering approach: artificial bee colony (ABC) algorithm[J]. Applied Soft Computing , 2011, 11 (1) : 652-657 DOI:10.1016/j.asoc.2009.12.025 |
| [83] | HSIEH T J, HSIAO H F, YEH W C. Forecasting stock markets using wavelet transforms and recurrent neural networks: an integrated system based on artificial bee colony algorithm[J]. Applied Soft Computing , 2011, 11 (2) : 2510-2525 DOI:10.1016/j.asoc.2010.09.007 |
| [84] | HORNG M H. Multilevel thresholding selection based on the artificial bee colony algorithm for image segmentation[J]. Expert System with Applications , 2011, 38 (11) : 13785-13791 |



